数据结构与算法详解——二叉查找树篇(附c++实现代码)
目录
- 二叉树相关概念和术语
-
- 二叉树特殊类型
- 二叉树的存储
-
- 链式存储
- 顺序存储
- 二叉树的遍历
- 二叉查找树
-
- 查找
- 插入
- 删除
- 完整代码
- 时间复杂度分析
二叉树相关概念和术语
二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。
- 度:一个节点拥有子树的数目称为结点的度,叶子结点的度为0。
- 叶子结点:也称为终端结点,没有子树的结点或者度为零的结点。
- 结点的层次:从根结点开始,假设根结点为第1层,根节点的子结点为第2层,依此类推,如果某一个结点位于第L层,则其子结点位于第L+1层。
- 二叉树结点的深度:指从根节点到该结点的最长简单路径边的条数。
- 二叉树结点的高度:指从该节点到叶子结点的最长简单路径边的条数。

结点A的度为2,结点C的度为1,叶子结点为GHIJKL,度都为0。
结点的高度,深度,层数如图(注意高度和深度有的地方从0开始计数,有的地方从1开始计数)
二叉树特殊类型
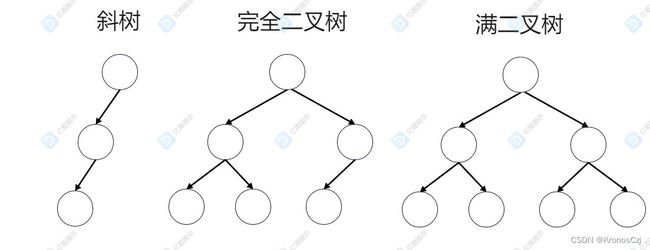
斜树不多赘述,一般是退化成链表的形式时导致性能下降的情形。
完全二叉树:深度为k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时,称为完全二叉树(叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部)。
满二叉树:如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上。满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
二叉树的存储
链式存储
template <typename T>
struct treeNode {
T data;
treeNode<T>* left;
treeNode<T>* right;
};
结点的定义:存储的数据,左子树指针,右子树指针。
顺序存储
我们把结点存储在数组中,父节点存储在下标为i的位置,那么左子树存储在2*i的位置,右子树存储在2*i+1的位置。举个例子,假设根结点存储在下标为i=1的位置,那么根结点的左子树存储在2*i=2的位置,根结点的右子树存储在2*i+1=3的位置,以此类推。
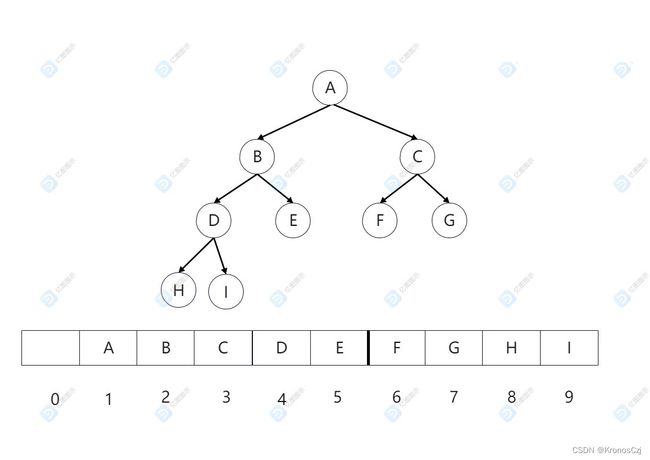
上图是一颗完全二叉树,使用顺序存储存储率就比较高,或者说空间利用率比较高。假设上图没有结点F,那么下标为6的位置就置空,不存储数据。
二叉树的遍历
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
以上面顺序存储中的完全二叉树为例子,
- 前序遍历:ABDHIECFG
- 中序遍历:HDIBEAFCG
- 后序遍历:HIDEBFGCA
递归实现
void preOrder(Node* root) {
if (root == null) return; //递归结束条件
std::cout<<root->data<<std::endl;
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node* root) {
if (root == null) return; //递归结束条件
inOrder(root->left);
std::cout<<root->data<<std::endl;
inOrder(root->right);
}
void postOrder(Node* root) {
if (root == null) return; //递归结束条件
postOrder(root->left);
postOrder(root->right);
std::cout<<root->data<<std::endl;
}
二叉查找树
二叉查找树又叫二叉搜索树,二叉排序树。
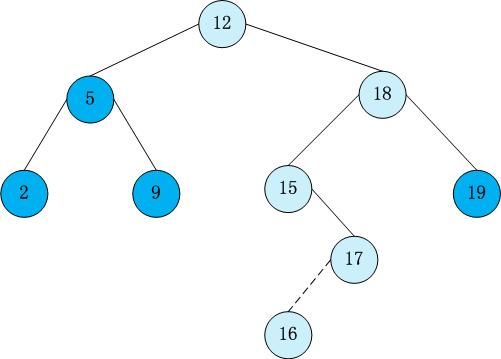
对于树中任意一个结点,左子树中的每一个结点的值都小于这个结点的值,右子树中的每一个结点的值都大于这个结点的值。下图就是一个二叉查找树的例子,可以看到根结点的左子树中每一个结点都小于12,根结点右子树中每一个结点都大于12。
查找
假设我们要查找的值为value,我们从根结点开始,比较结点的值和value的大小:
- 如果结点的值等于value,返回
- 如果结点的值比value小,那么在左子树递归查找
- 如果结点的值比value大,那么在右子树递归查找
template<typename T>
treeNode<T>* binarySearchTree<T>::find(T data) {
treeNode<T>* n = root;
while (n != nullptr) {
if (data > n->data)n = n->right;
else if (data < n->data)n = n->left;
else return n;
}
return nullptr;
}
这里使用了非递归的写法,逻辑应该是比较清晰了。
插入
插入就是查找到一个能插入的位置,所以和上面查找的过程很类似。
假设我们要插入的值为value,我们从根结点开始,比较结点的值和value的大小:
- 如果结点的值比value小,那么就看结点的右子树是否为空,如果为空就将value插入到结点的右子树,如果不为空就在右子树递归插入
- 如果结点的值比value大,那么就看结点的左子树是否为空,如果为空就将value插入到结点的左子树,如果不为空就在左子树递归插入
template<typename T>
void binarySearchTree<T>::insert(T data) {
if (root == nullptr) {
root = new treeNode<T>(data);
return;
}
treeNode<T> *n = root;
while (n != nullptr) {
if (data > n->data) {
if (n->right == nullptr) {
std::cout << n->data << "->right=" << data << std::endl;
n->right = new treeNode<T>(data);
return;
}
n = n->right;
}
else if (data < n->data) {
if (n->left == nullptr) {
std::cout << n->data << "->left=" << data << std::endl;
n->left = new treeNode<T>(data);
return;
}
n = n->left;
}
else //如果是相同的值就不用插入了,这里不支持重复值
return;
}
}
这里也使用了非递归的写法,逻辑也是比较清晰了,需要注意的是要先判断root是否为空,如果为空就直接将插入的结点作为根结点。
删除
删除相对来说就比较复杂了,需要分三种情况讨论:要删除的结点有0个、1个、2个子结点(假设要删除的结点为n):
n有0个子结点,即n是叶子结点:直接将父节点指向n的指针置为nullptr就可以了。
n有1个子结点,将父节点指向n的指针 重新赋值指向 n的子结点。
n有2个子结点,我们要找到一个结点顶替n,这个结点必须是大于n的第一个结点或者小于n的最后一个结点,分别对应【n的右子树】中最小的结点和【n的左子树】中最大的结点。这里我们使用【n的右子树】中最小的结点,就是遍历【n的右子树】的左子树,直到叶子结点,然后交换这个结点和n的位置,删除结点n。在代码的实现中我们用了一种取巧的方法,下面会讲述。

如果要删除结点20,那么将结点18的右子树置为nullptr,然后释放结点20的空间。
如果要删除结点14,那么将结点18的左子树指向结点13,然后释放结点14的空间。
如果要删除结点8,我们要先找到结点8的右子树中的最小值,也就是在结点9,交换结点8和结点9的位置,然后删除结点8。
template<typename T>
void binarySearchTree<T>::remove(T data) {
if (root == nullptr)return;
treeNode<T>* n = root, * parent = nullptr; //n指向要删除的结点,parent是n的父节点
while (n != nullptr && n->data != data) {
parent = n;
if (data > n->data)n = n->right;
else n = n->left;
}
if (n == nullptr) {
std::cout << "remove() : cant find data=" << data << std::endl;
return;
}
//情况一:要删除的结点n有两个子节点
if (n->left != nullptr && n->right != nullptr) {
treeNode<T>* min = n->right; //min:n右子树中最小的结点
treeNode<T>* min_parent = n; //min_parent:min的父节点
while (min->left != nullptr) {
min_parent = min;
min = min->left;
}
n->data = min->data; //这里取巧将min和n的data进行交换
n = min; //那么要删除的结点n变成了min
parent = min_parent; //注意此时parent已经是原来min(n)的父节点了
//注意这里比较巧妙的点:要删除的节点已经从 参数给定的data的节点 转移为 删除min了
//min是绝对没有左子树的,所以min只能是有一个子节点(右子树)或者没有子节点的,刚好符合下面的情况二和情况三
//所以接着运行就可以删除min(即n)
}
//情况二:要删除的结点n有且只有一个子节点
treeNode<T>* child; //n的子节点
if (n->left != nullptr)
child = n->left;
else if (n->right != nullptr)
child = n->right;
else //情况三:要删除的结点n没有子节点
child = nullptr;
if (parent == nullptr) //要删除的是根节点
root = child;
else if (parent->left == n)
parent->left = child;
else
parent->right = child;
delete n;
}
首先是要先找到要删除的结点,这里和查找类似,但是需要多一个变量parent要存储要删除的结点的父节点。
注意这里的处理不同情况的顺序和我们上面说的顺序相反,这里先处理有两个子结点的情况:和上面说的一样,要找到n的右子树中最小的结点,存储在min中,min_parent存储min的父节点。然后我们这里不是交换结点,而是交换n和min的值,没有任何指针的改变,那么现在问题就转换成了 要删除原来min的那个结点(因为交换,现在的值已经是n的值了)。
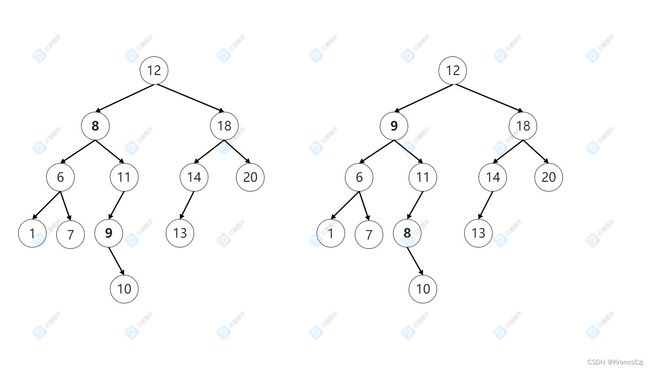
举个例子说明,我们现在要删除左图中的结点8,我们找到结点8的右子树中的最小值结点9,交换结点8和结点9的值变成了右图中的样子,现在的问题是不是就变成了删除右图中的结点8?注意右图中的结点8一定是叶子结点或者只有右子树的(不可能有左子树,因为如果有左子树,左子树才是最小值),那么现在就转换成了另外两种情况了,所以我们的代码中先写这种情况。
剩余的两种情况就简单了,看代码应该能看得懂了。
完整代码
#ifndef BINARY_SEARCH_TREE
#define BINARY_SEARCH_TREE
#include 时间复杂度分析
从上面查找、插入和删除的分析来看,二叉查找树的查找,插入和删除的时间复杂度其实和树的高度h成正比,所以时间复杂度都是O(h)。现在问题就转换成了求二叉查找树的高度h,让我们来看看下面几种情况:
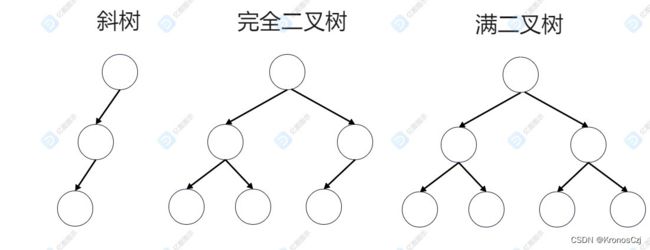
斜树的高度明显就是n,因此查找,插入和删除的时间复杂度是O(n),此时的二叉查找树极度不平衡,退化成链表了。
假设完全二叉查找树有L层,第L层的叶子结点个数在[1, 2^(L-1)] 区间内(满二叉查找树第x层结点的个数为2^(x-1))。 从1到(L-1)层的结点个数总和为1+2+4+…+2^(L-2) = 2^(L-1)-1。
因此L层的完全二叉树的结点总个数在[2^(L-1) , 2^L-1]区间内,L在[log2(n+1),log2(n)+1]区间内,h=L-1,所以h在[log2(n+1)-1,log2(n)]区间内,所以完全二叉查找树的查找、插入和删除的时间复杂度是O(logn)。
可以看出,比较平衡的二叉查找树的性能是比较好的,但是在不平衡乃至极端的斜树的情况下,性能就下降的比较明显,因此为了避免性能的退化,就有了各种平衡的二叉查找树的设计,让性能稳定在O(logn),像AVL树,红黑树等等。