详解：二叉排序树（二叉查找树）的代码实现——Scala

     

目录

二叉排序树的定义

 二叉树的代码实现

1、插入节点

2、中序遍历节点

3、查找指定节点

4、删除指定节点❤

二叉排序树完整代码

---

        二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

二叉排序树的定义

一棵空树，或者是具有下列性质的二叉树：
        （1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值
        （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值
        （3）左、右子树也分别为二叉排序树
        （4）没有键值相等的结点

        下面演示创建一棵二叉树，创建节点顺序为：Array(8, 4, 12, 9, 10, 1, 6, 7, 5, 15, 13, 3)：

 二叉树的代码实现

        备注：

        1、为了方便初学者理解，本文庖丁解牛，将二叉树代码一一分割，旨在逐个击破。

        2、文末有附上完整的代码。

        3、代码中也有详细的注解，基础扎实的读者可以不必理会文中的长篇大论，直接阅读代码。

1、插入节点

向二叉排序树中插入节点步骤：

1. 如果根节点为空，第一次插入，根节点为第一次插入的元素
2. 如果根节点不为空，不是第一次插入，则调用root.add(ele)方法插入
3. root.add(ele)方法中，逻辑如下：
   1. 如果小于等于当前值, 则往左子树添加，如果左子树数为空，直接置为新节点，否则递归向左子树添加
   2. 如果大于当前值，则往右子树添加，如果右子树数为空，直接置为新节点，否则递归向右子树添加。

        备注： 在二叉排序树的定义中，不同的数据结构教材中均有不同的定义方式，不同点在于二叉排序树是否存入相同的值，即有没有键值相等的节点。百度百科中说明，不同的定义都视为正确。所以，本文代码中左子树可以存入小于等于根节点的值。

百度百科

定义三

一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

【注】：以上的三种定义在不同的数据结构教材中均有不同的定义方式， 但是都是正确的 ，在开发时需要根据不同的需求进行选择。

        代码实现：

//二叉排序树的节点
class SBTreeNode[T: Ordering](var value: T) {
  // 从冥界召唤可以比较 T 类型的比较器(Ordering)
  private val orderValueT: Ordering[T] = implicitly[Ordering[T]]
  // 父节点
  var p: SBTreeNode[T] = _
  // 左节点
  var left: SBTreeNode[T] = _
  // 右节点
  var right: SBTreeNode[T] = _

  // 插入节点
  def add(ele: T): Unit = {
    // 如果小于等于当前值, 则在左边添加
    if (orderValueT.lteq(ele, value)) {
      // 如果左节点是 null, 则左节点置为新节点
      if (left == null) {
        left = new SBTreeNode[T](ele)
        left.p = this
      }
      else // 否则递归的在左节点添加节点
        left.add(ele)
    } else { // 否则向右边添加
      if (right == null) {
        right = new SBTreeNode[T](ele)
        right.p = this
      }
      else right.add(ele)
    }
  }
}


// 排序二叉树
class SearchBinaryTree[T: Ordering] {
  // 排序二叉树的根节点
  var root: SBTreeNode[T] = _

  // 向排序二叉树中添加节点
  def add(ele: T): Unit = {
    // 如果 root 节点为 null, 则把元素置为 root 位置
    if (root == null)
      root = new SBTreeNode[T](ele)
    // 如果 root 节点不为空则调用 root 的 add 方法来添加元素
    else
      root.add(ele)
  }
}

2、中序遍历节点

  二叉树的遍历有三种遍历方式，分别是：

        （1）先(根)序遍历（根左右）

        （2）中(根)序遍历（左根右）

        （3）后(根)序遍历（左右根）

        对于二叉排序树来说，中序遍历的结果是由小到大排序，这也是二叉排序树的特点，所以，本文在遍历二叉排序树时采用中序遍历。

中序遍历的步骤：

1. 如果根节点为空，则打印：二叉排序树为空！！！
2. 否则调用root.infixForeach(op)方法进行遍历
3. root.infixForeach(op)的逻辑为：
   1. 只要左节点不为空，则递归遍历左子树
   2. 输出当前节点值
   3. 只要右节点不为空，则递归遍历右子树

代码实现：

//二叉排序树的节点
class SBTreeNode[T: Ordering](var value: T) {
  // 从冥界召唤可以比较 T 类型的比较器(Ordering)
  private val orderValueT: Ordering[T] = implicitly[Ordering[T]]
  // 父节点
  var p: SBTreeNode[T] = _
  // 左节点
  var left: SBTreeNode[T] = _
  // 右节点
  var right: SBTreeNode[T] = _

 // 中序遍历节点
  def infixForeach(op: T => Unit): Unit = {
    if (left != null) left.infixForeach(op)
    op(value)
    if (right != null) right.infixForeach(op)
  }
}


// 二叉排序树
class SearchBinaryTree[T: Ordering] {
  // 二叉排序树的根节点
  var root: SBTreeNode[T] = _

 // 中序遍历二叉树
    def infixForeach(op: T => Unit): Unit = {
      if (root == null)
        println("二叉排序树为空！！！")
      else
        root.infixForeach(op)
  }
}

代码运行中序遍历的结果：

        从结果中，可以很直观的看到，插入一组无序的数，输出一组有序的数。

3、查找指定节点

查找指定节点逻辑如下：

1. 如果根节点为空，返回null
2. 否则调用searchNode(ele)函数查找指定节点
3. searchNode(ele)函数的逻辑为：
   1. 如果小于当前节点, 则递归查找左子树
   2. 如果大于当前节点, 则递归查找右子树
   3. 如果等于当前节点, 则直接返回当前节点
   4. 否则，返回null

代码实现：

//二叉排序树的节点
class SBTreeNode[T: Ordering](var value: T) {
  // 从冥界召唤可以比较 T 类型的比较器(Ordering)
  private val orderValueT: Ordering[T] = implicitly[Ordering[T]]
  // 父节点
  var p: SBTreeNode[T] = _
  // 左节点
  var left: SBTreeNode[T] = _
  // 右节点
  var right: SBTreeNode[T] = _

  // 查找节点
  def searchNode(ele: T): SBTreeNode[T] = {
    // 如果小于当前节点, 则去左边查找
    if (orderValueT.lt(ele, value) && left != null)
      left.searchNode(ele)

    // 如果大于当前节点, 则去右边查找
    else if (orderValueT.gt(ele, value) && right != null)
      right.searchNode(ele)

    // 如果和当前节点的值相等, 则返回当前节点
    else if (orderValueT.equiv(ele, value))
      this

    // 如果没有找到, 则返回null
    else null
  }
 
}


// 二叉排序树
class SearchBinaryTree[T: Ordering] {
  // 二叉排序树的根节点
  var root: SBTreeNode[T] = _

 // 查找节点
  def searchNode(ele: T): SBTreeNode[T] = {
    if (root == null) null
    else
      root.searchNode(ele)
  }
}

        备注：为了更好的输出查询结果，本文重写了toString方法，让输出结果显示为：当前节点值，和当前节点的父节点值。

                value= 12
                 p= 8

代码运行查询结果：

4、删除指定节点❤

        删除指定节点为二叉排序树的核心，也是逻辑最严谨的部分所在。删除节点需要考虑以下四种情况：

1. 删除根节点
2. 删除叶子节点
3. 删除只有一棵子树的节点
4. 删除有两棵子树的节点

        为了方便理解删除逻辑，读者可以先看以上四种情况的动画演示。

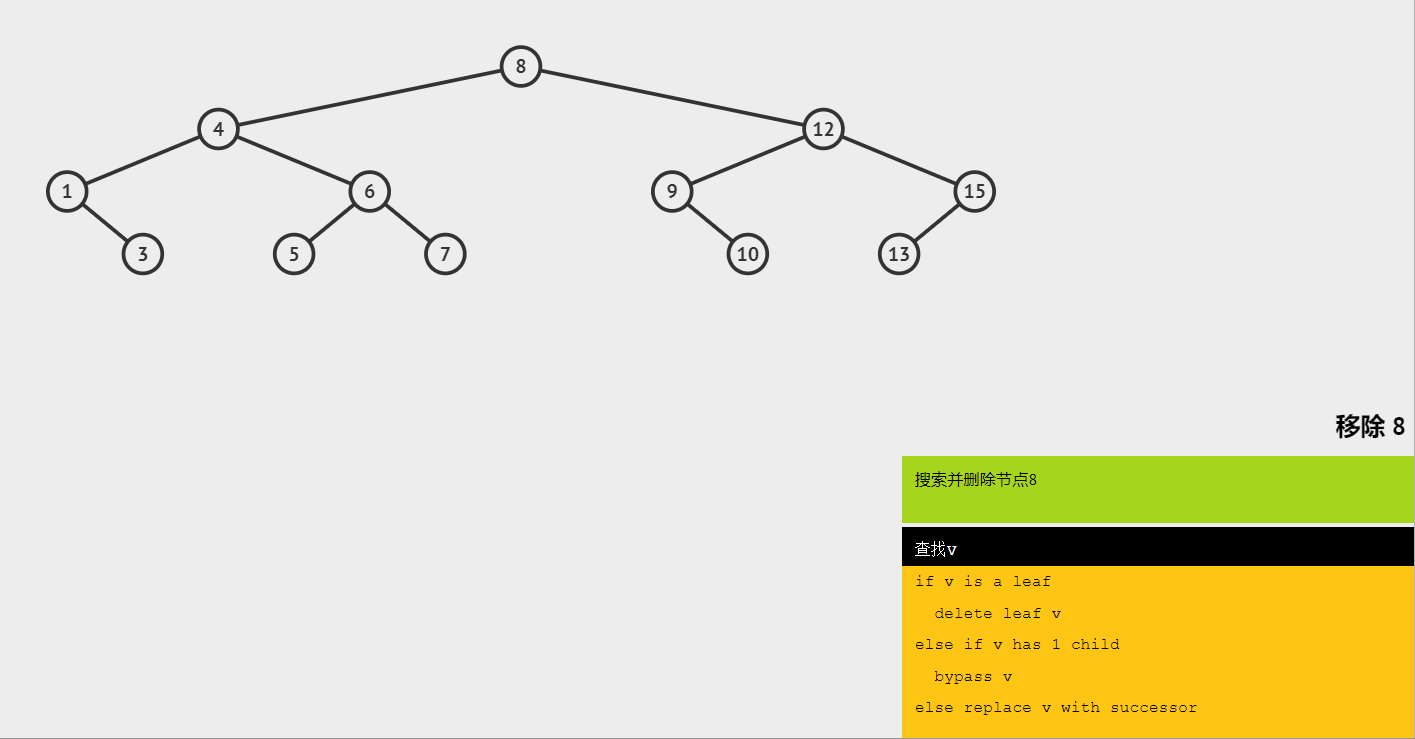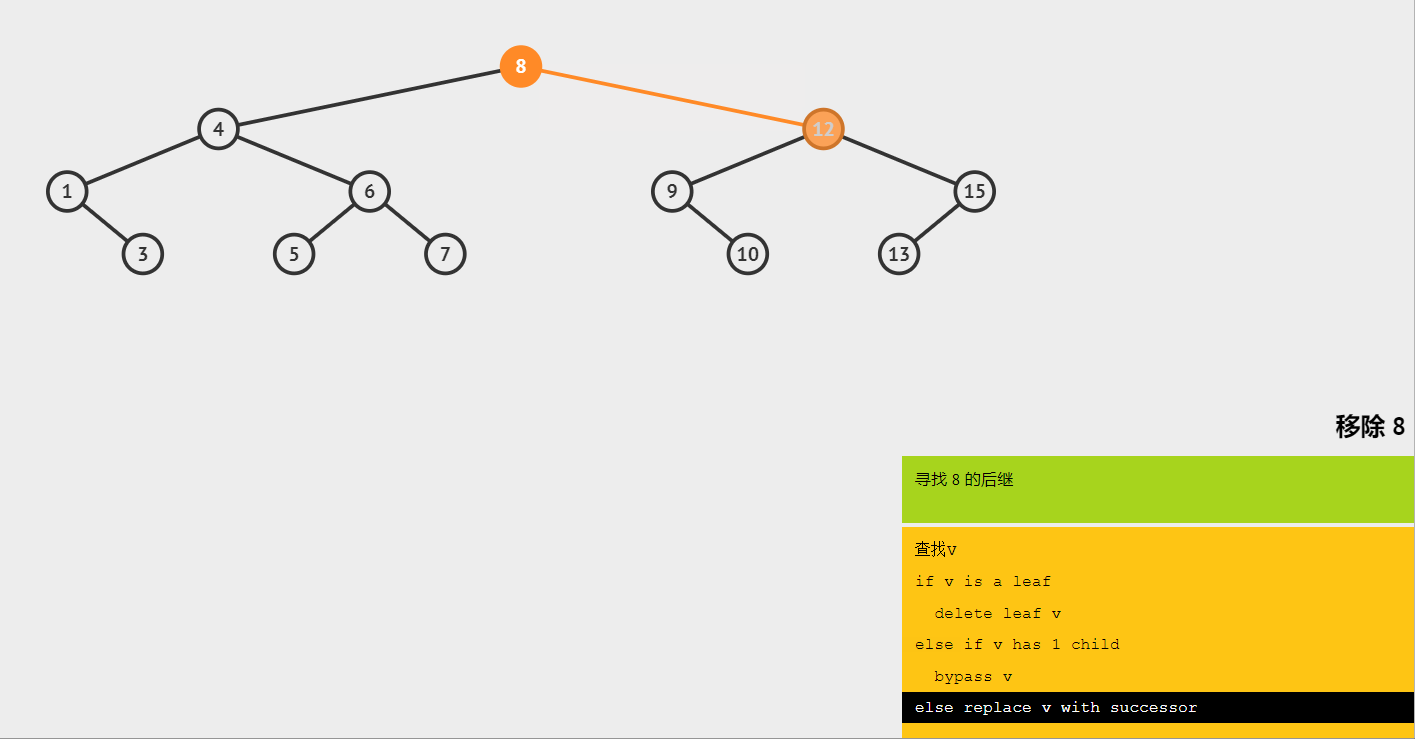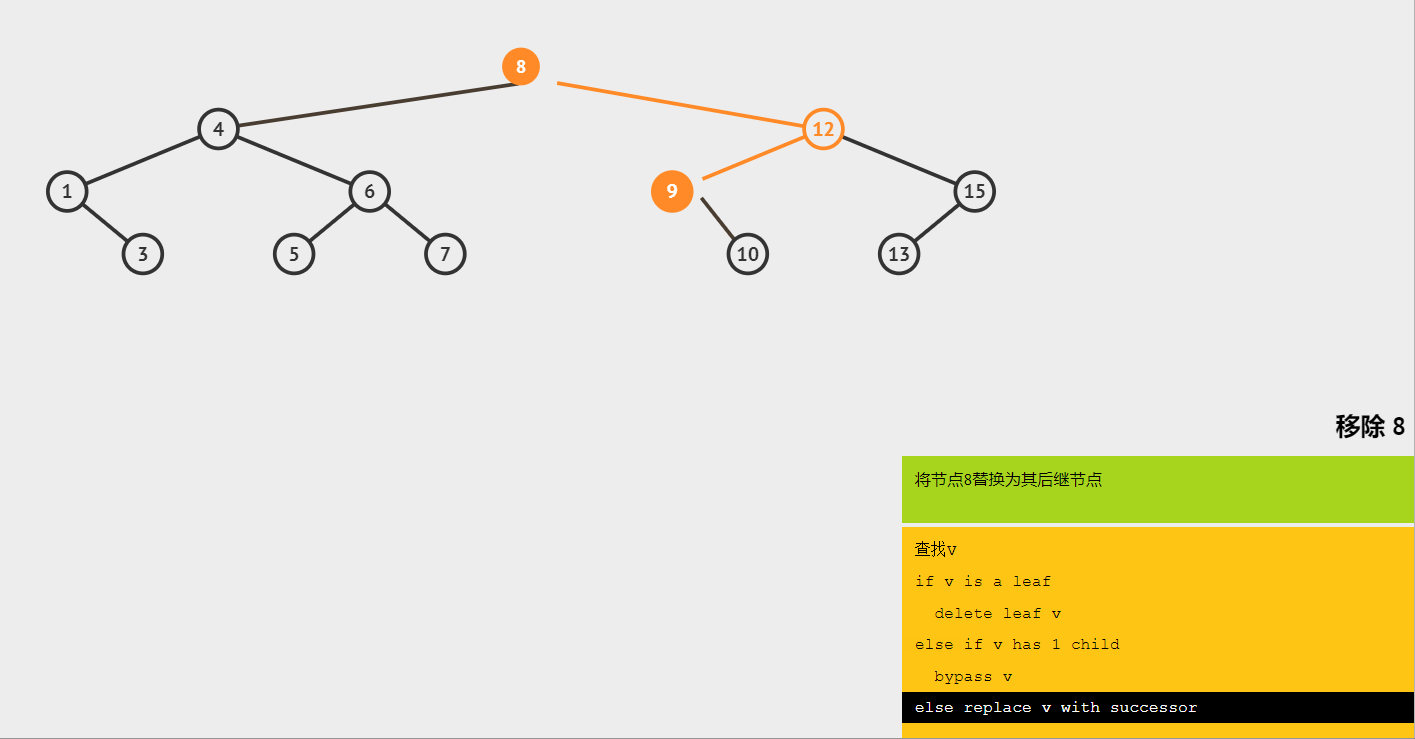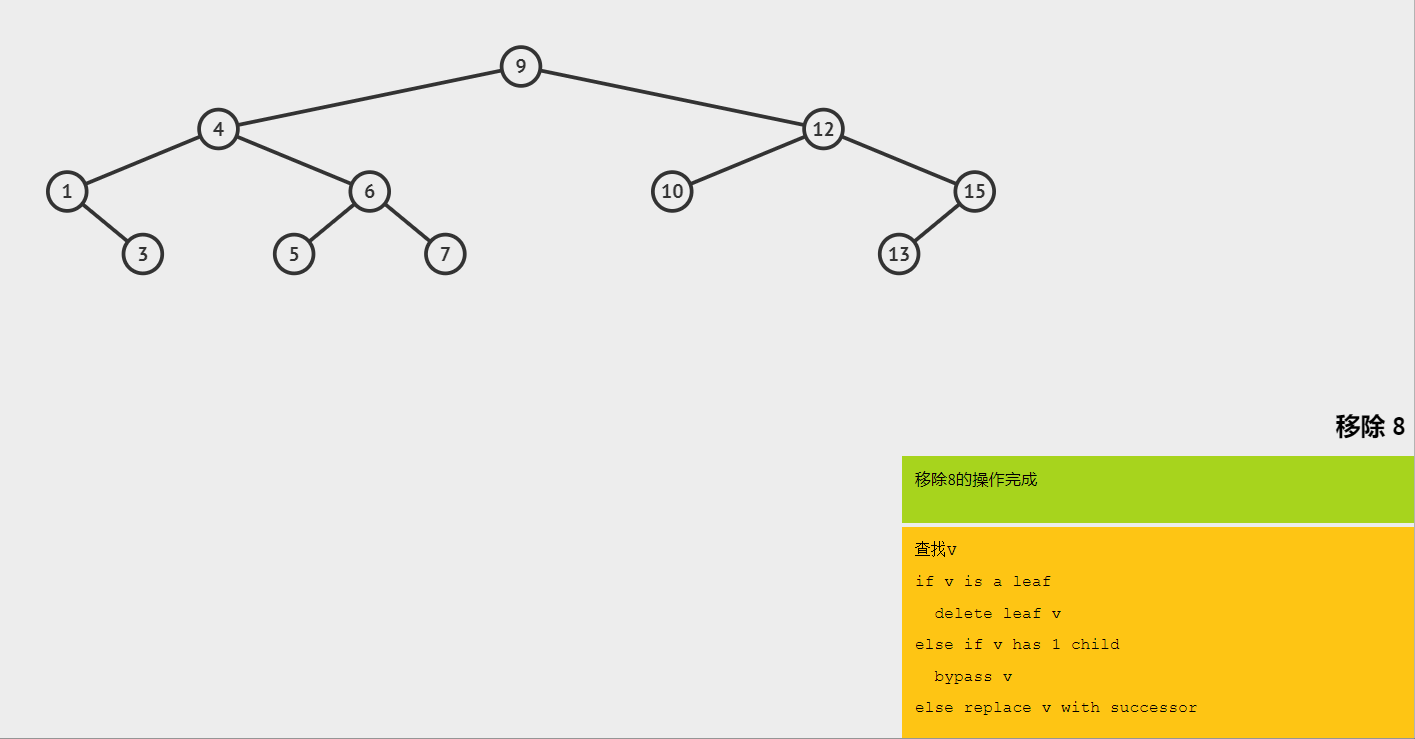
    （1）删除根节点 8，寻找 8 的后继节点 9，将后继节点 9 作为根节点。

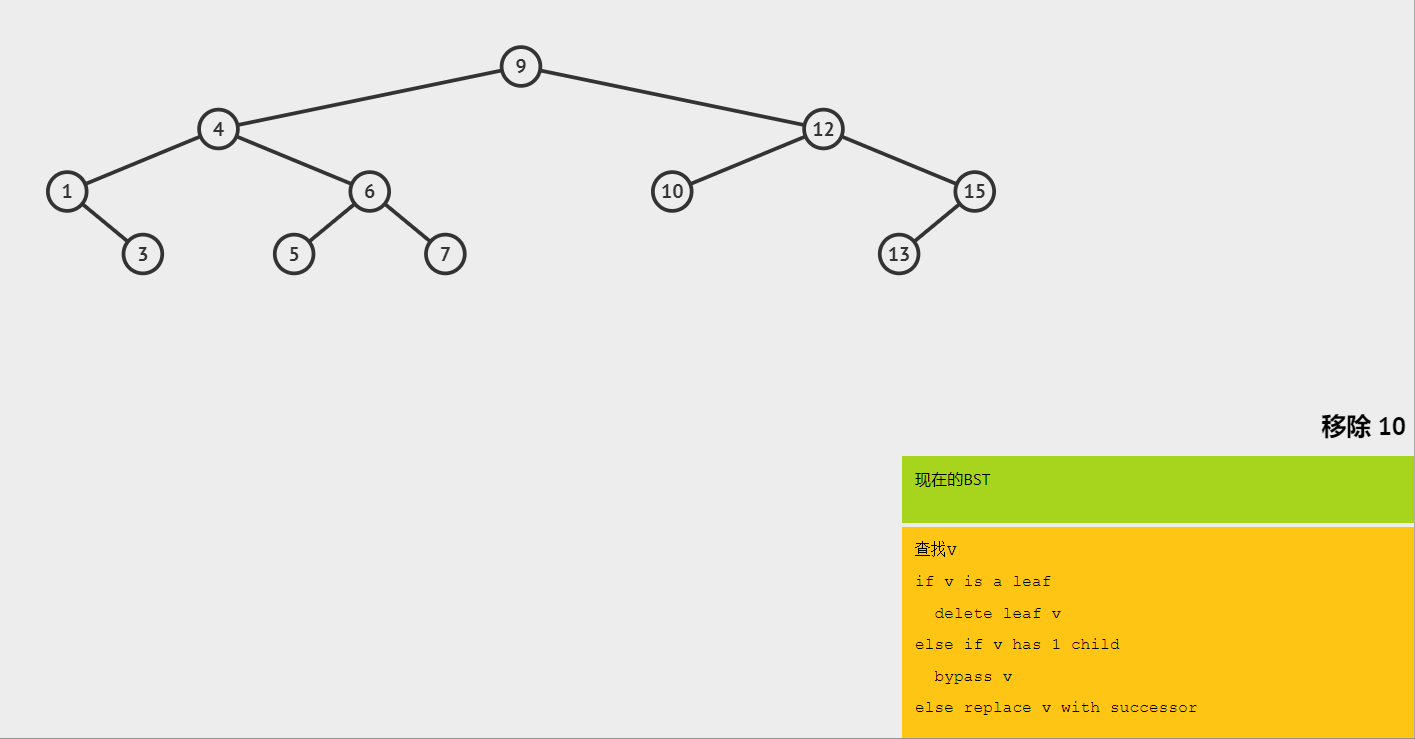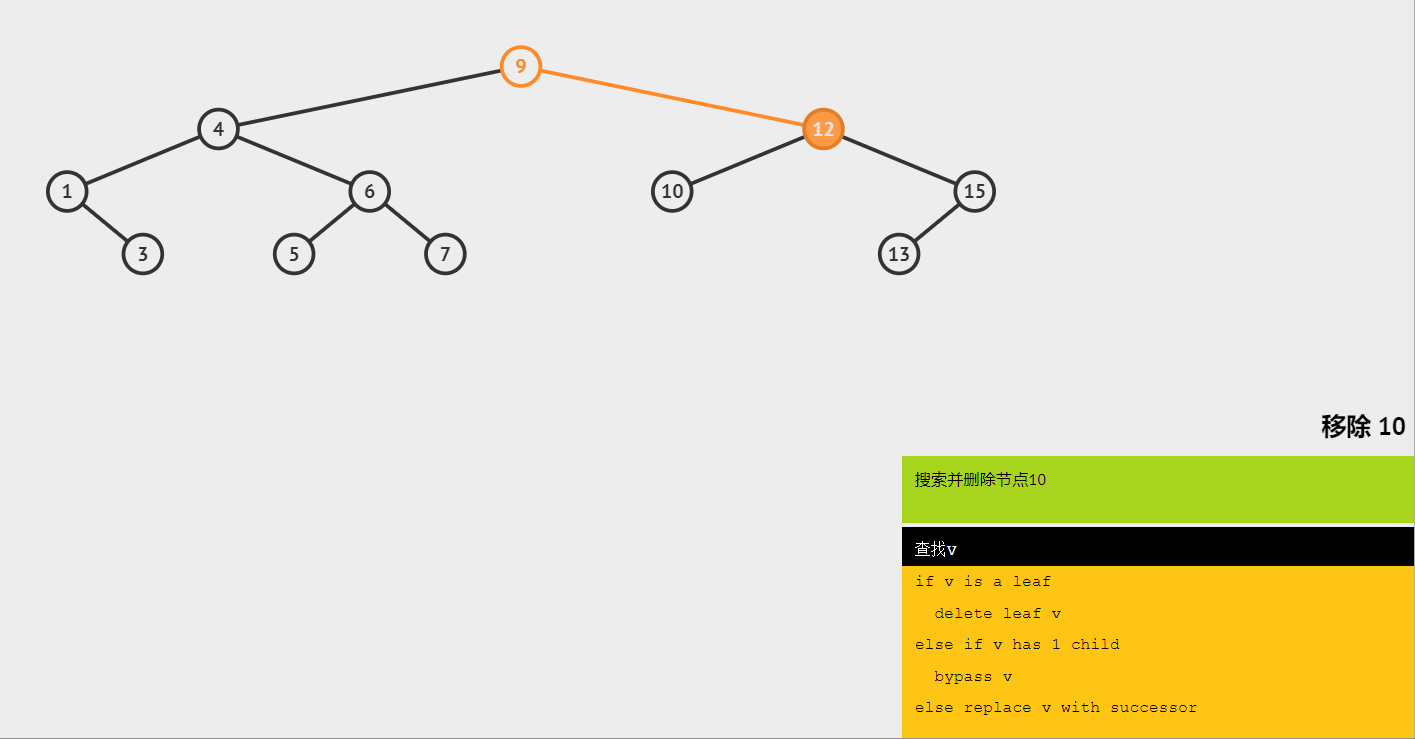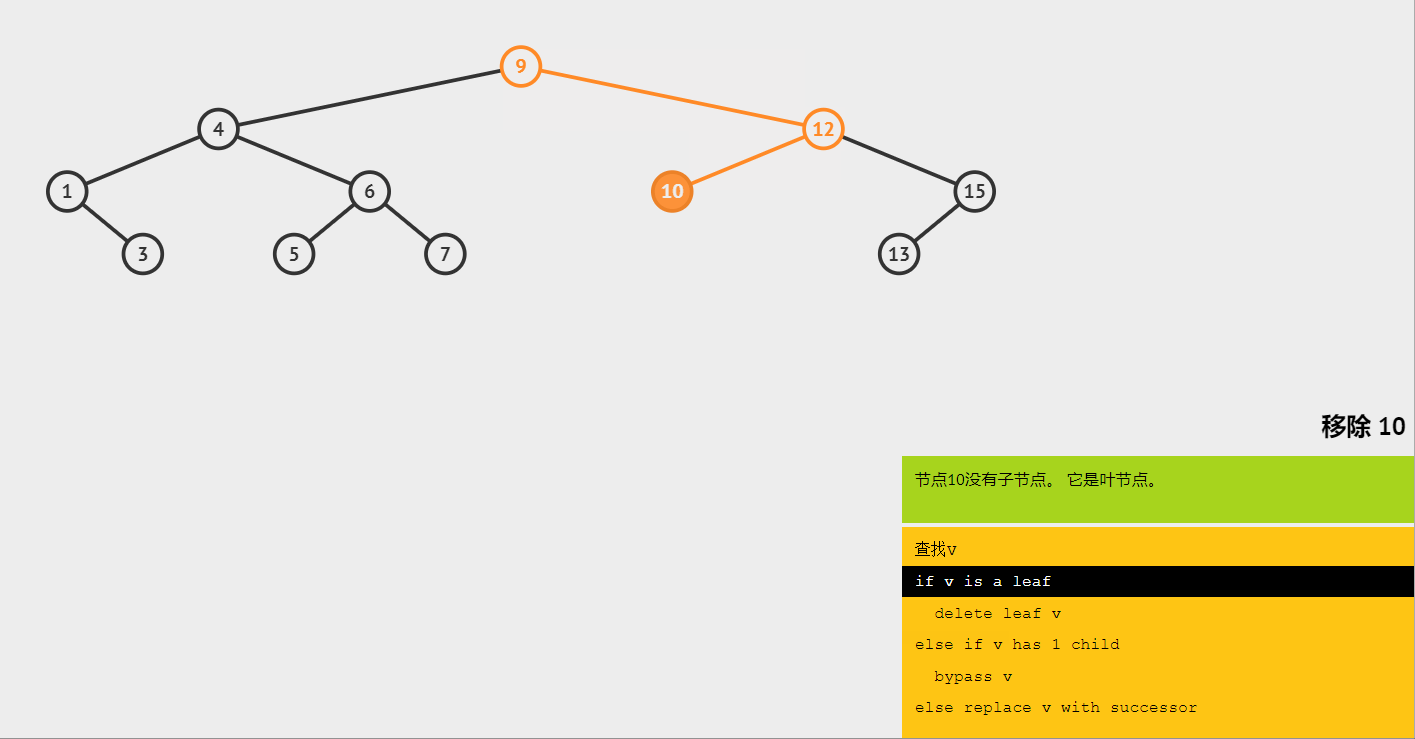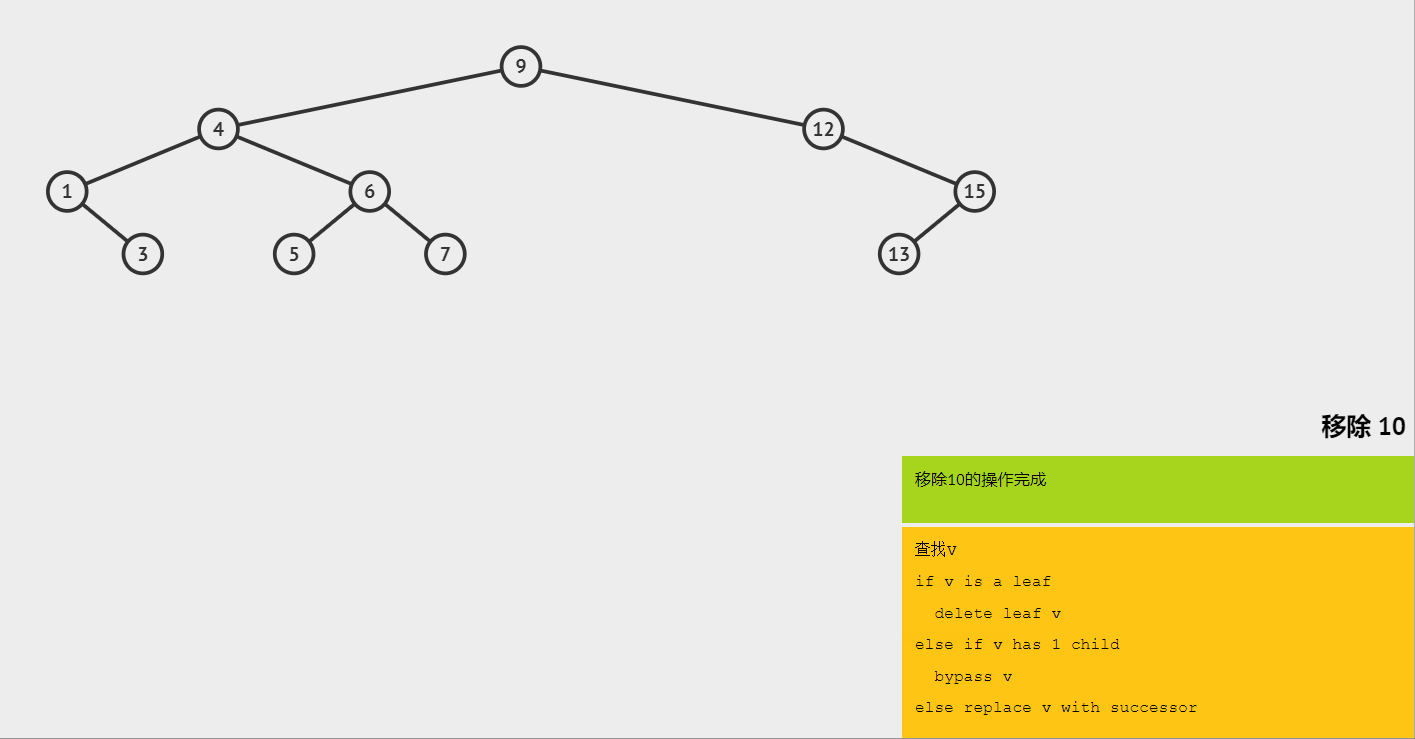
        （2）删除叶子节点10

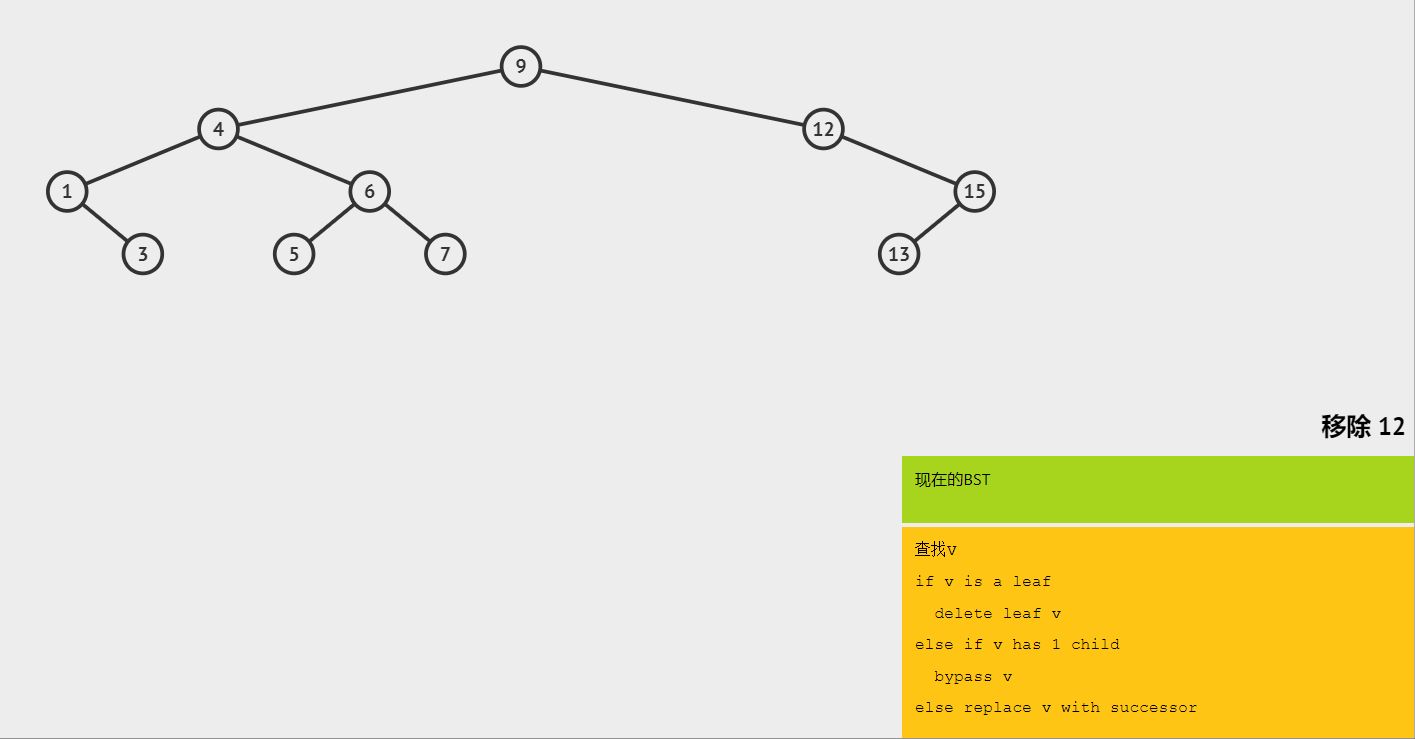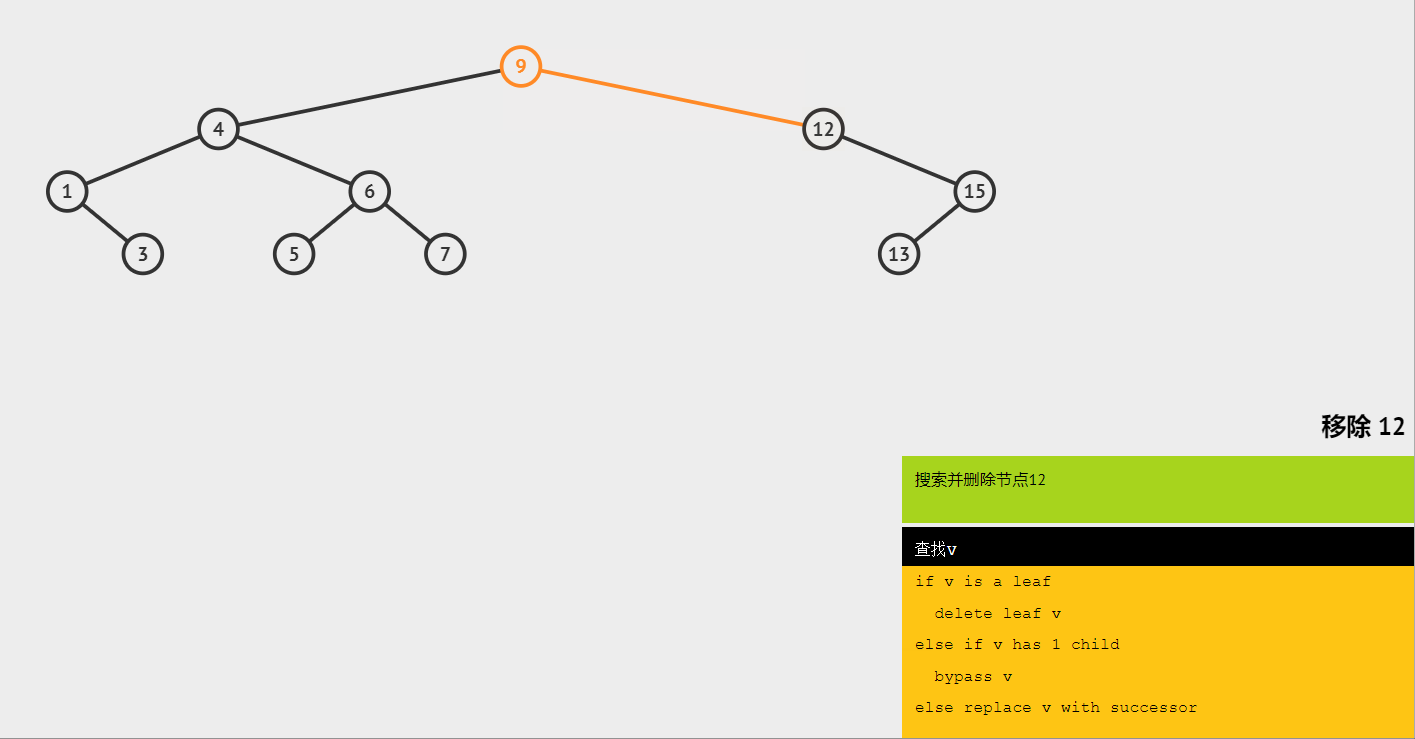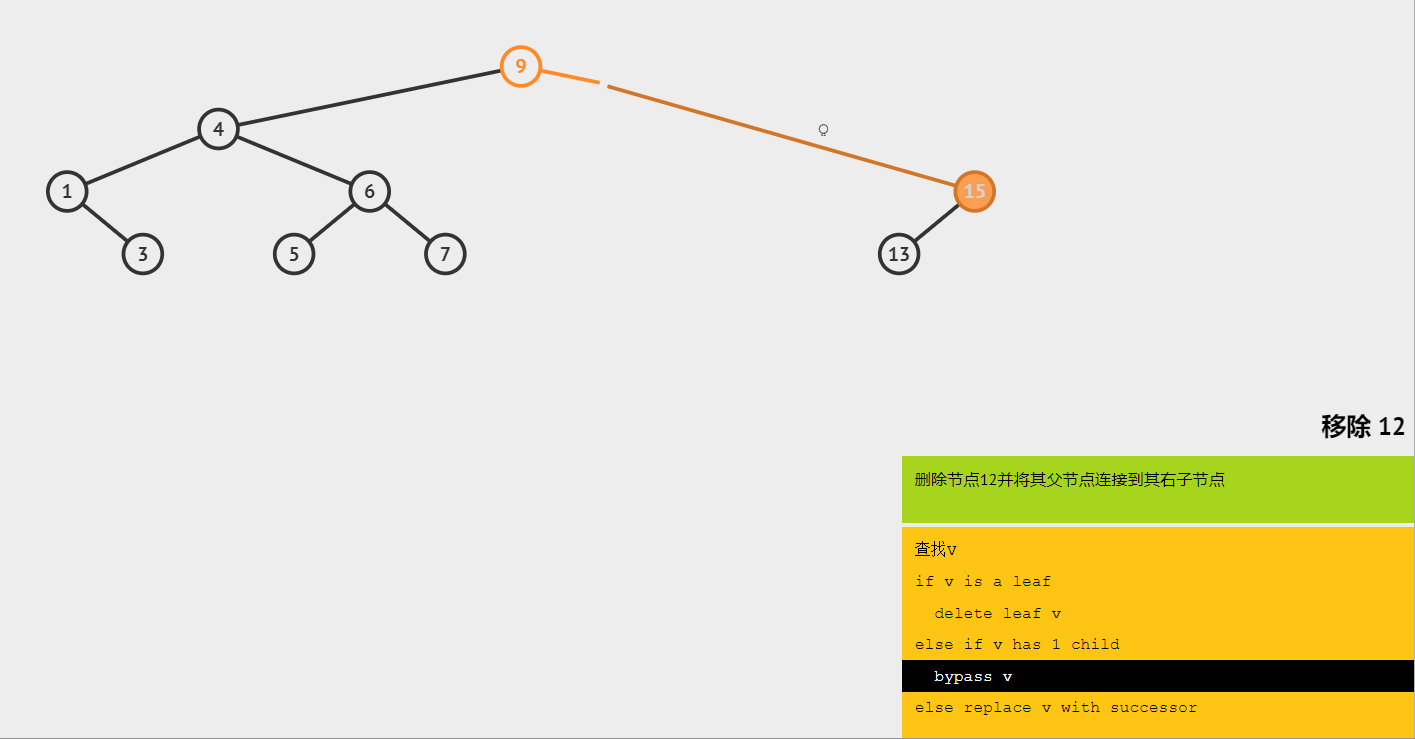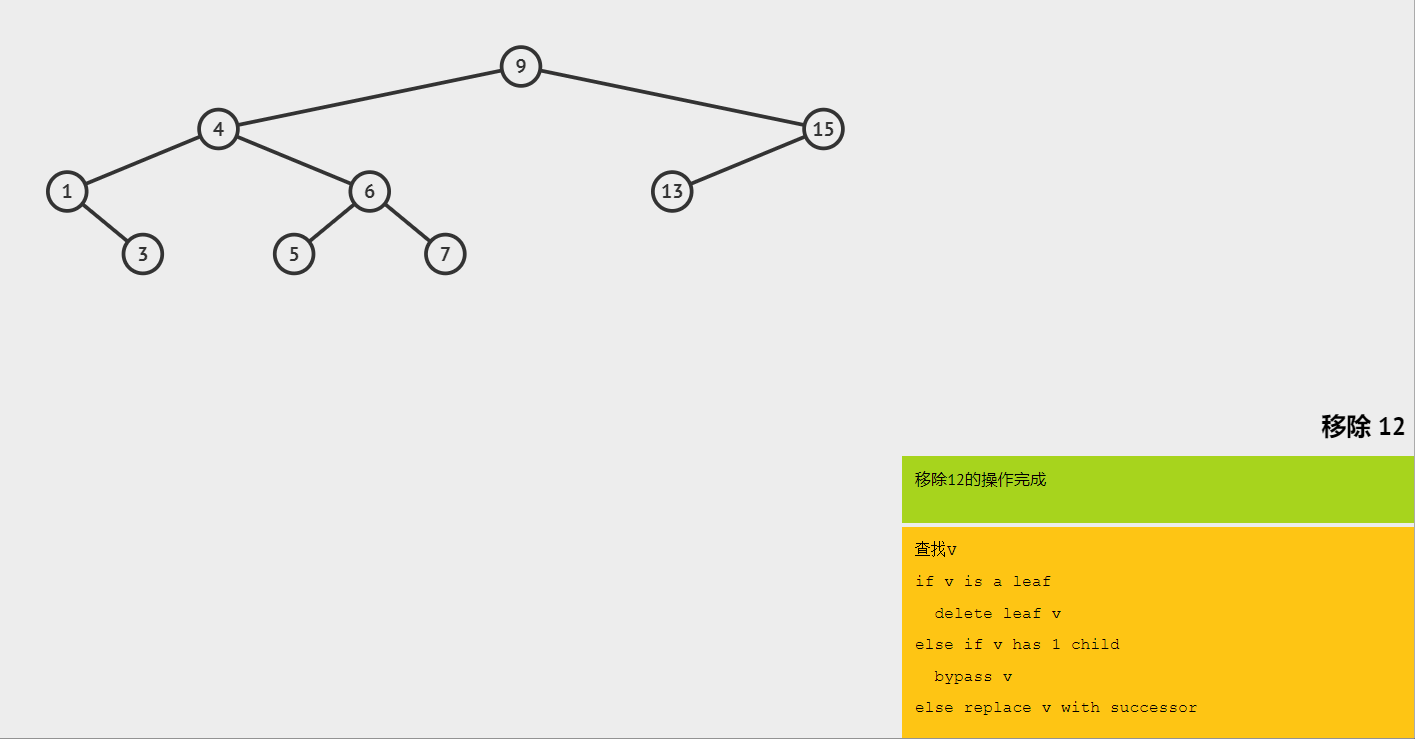
        （3）删除只有一棵子树的节点 12，将 15 连接到 9 的右节点上。

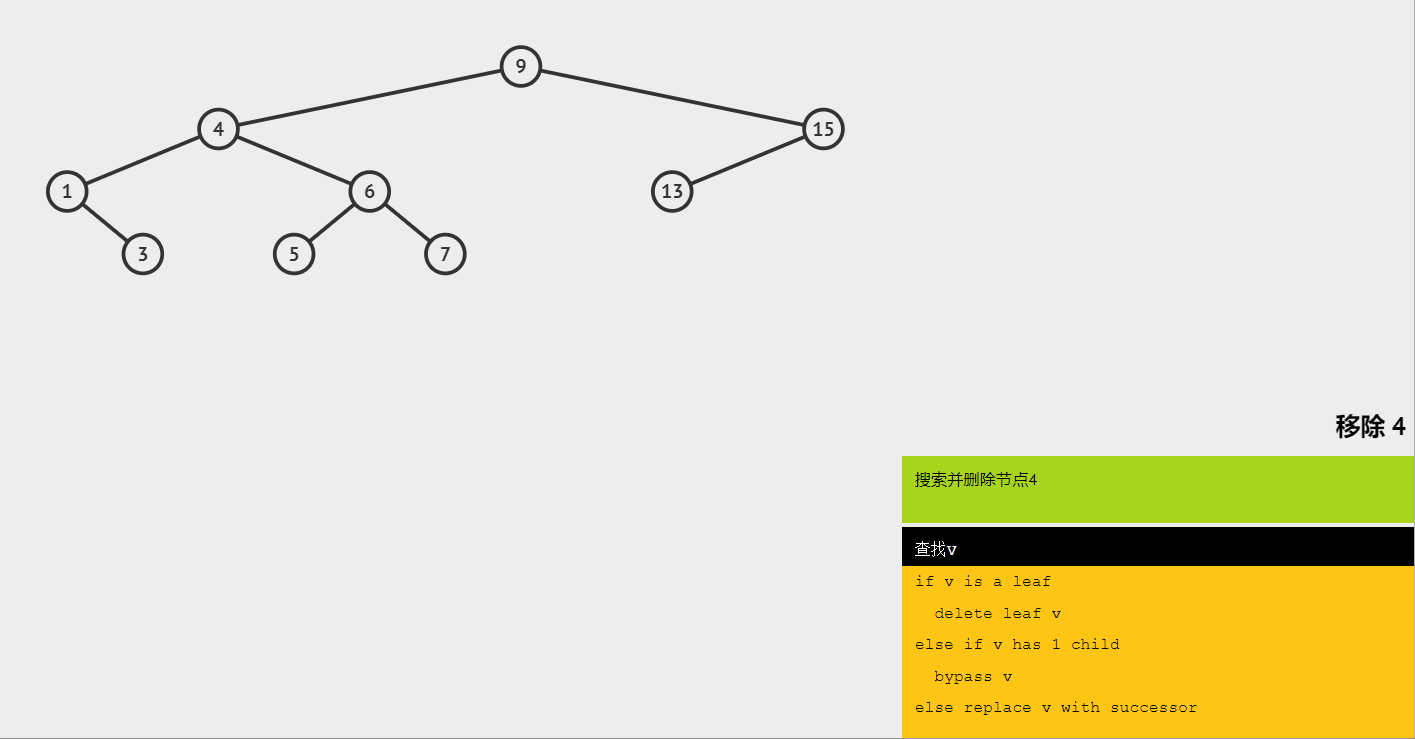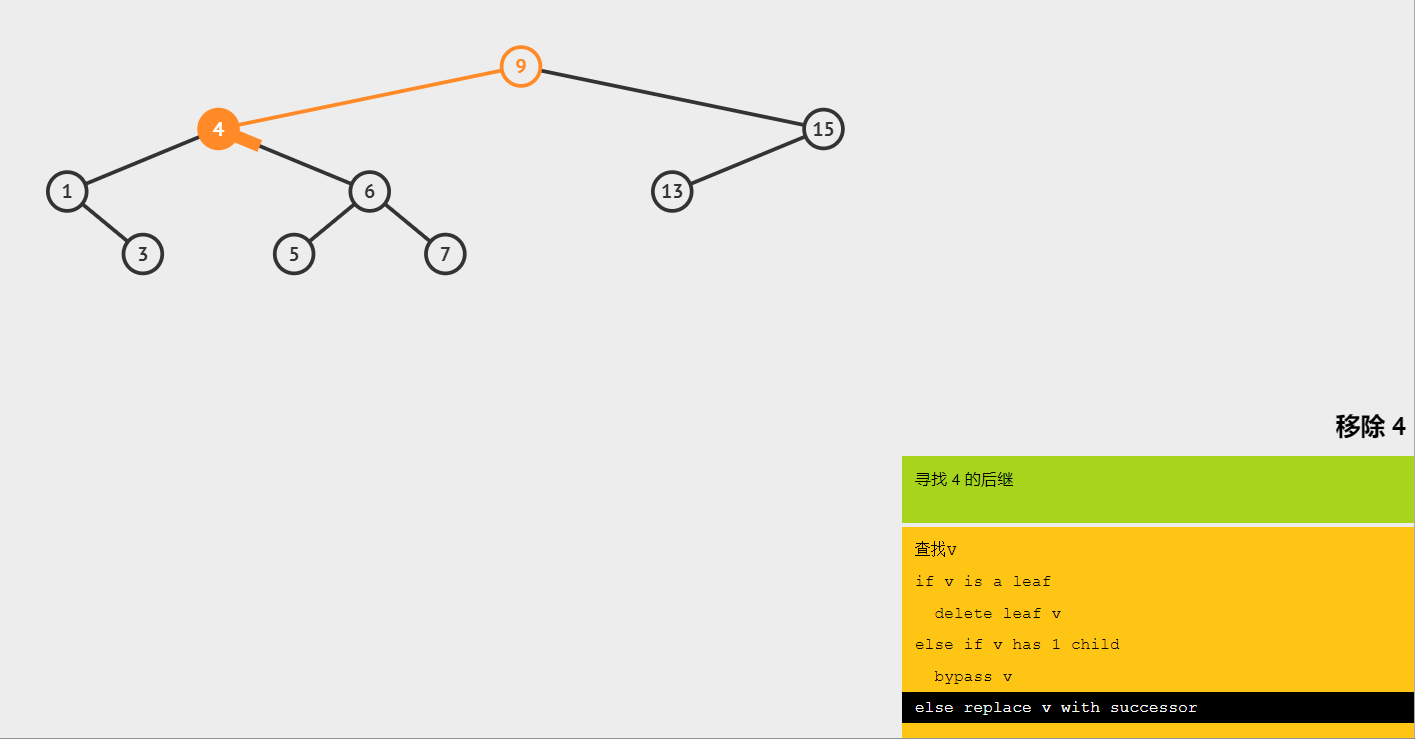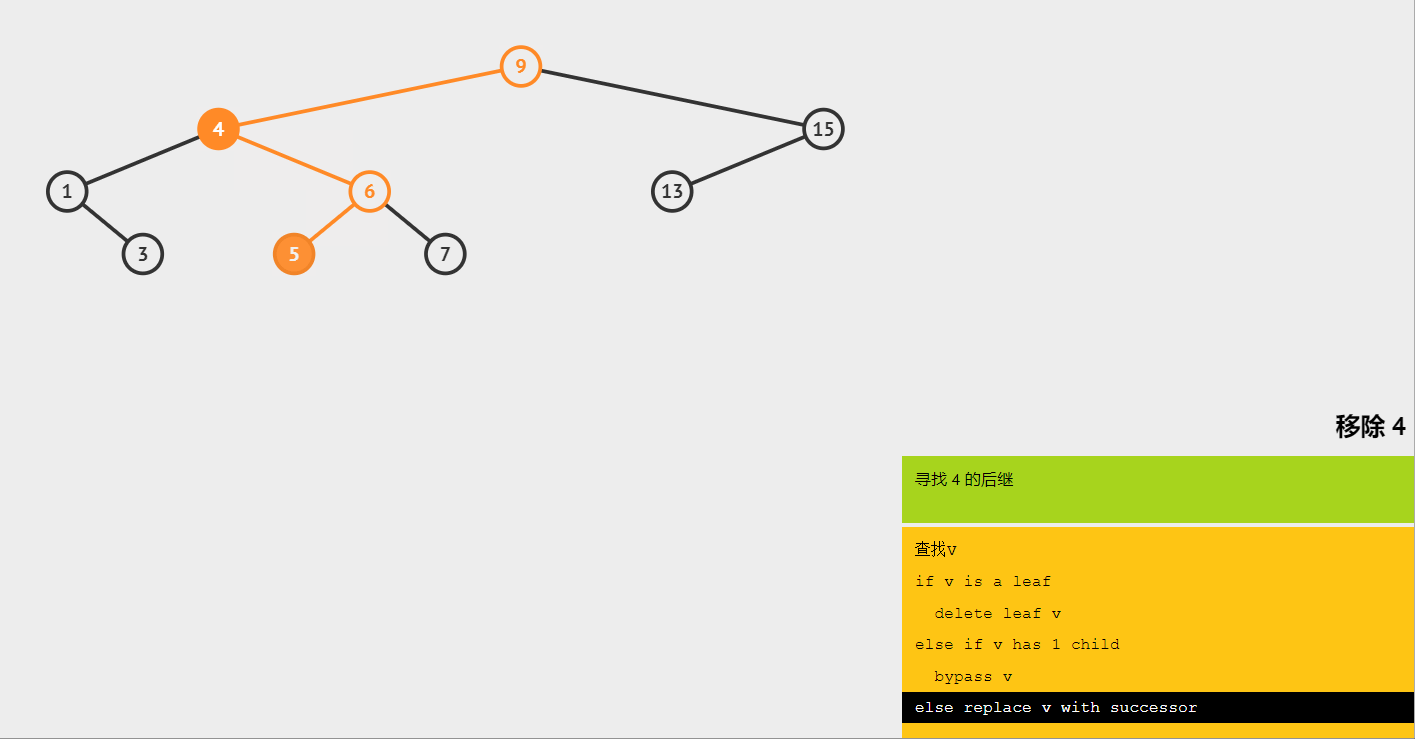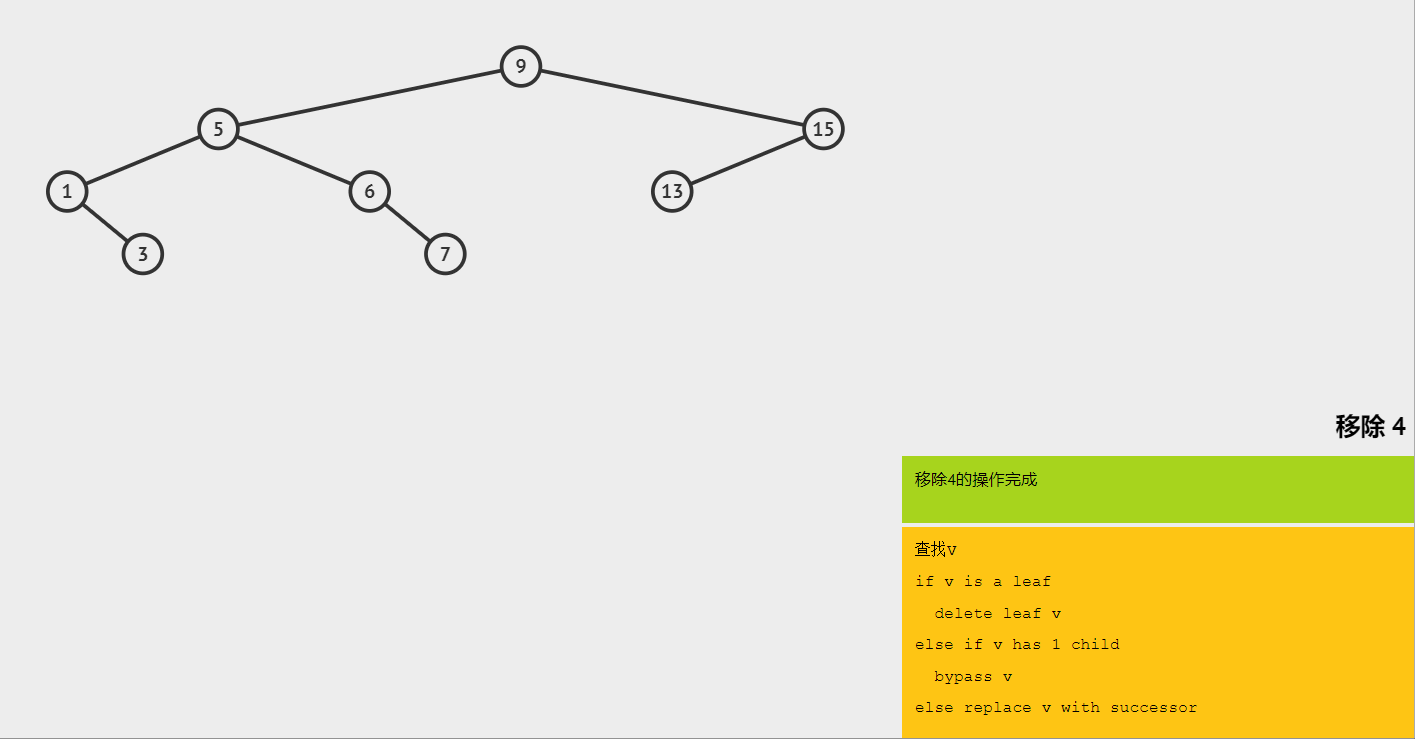
        （4）删除有两棵子树的节点 4，找到 4 的后继节点 5，将 5 替换 4。

         有了上述动画的演示，下面开始讲解如何用代码实现。

删除根节点的逻辑：

1. 如果根节点为空，则返回false，删除失败。
2. 如果根节点有两棵子树，则删除右子树的最小节点，并且用右子树的最小值代替根节点，即是寻找后继节点的过程，调用root.right.deleteMin方法现实。
   1. root.right.deleteMin的逻辑为：遍历左节点，找到最小的节点，删除最小的节点，并返回其值域。
3. 如果根节点只有一棵子树，则令根节点的孩子节点为根节点。
4. 否则，删除的就不是根节点，调用root.deleteSBT(ele)函数删除根节点的子节点。

删除子节点的逻辑：

1. 如果当前节点为要删除的节点，则继续判断，
   1. 如果当前节点为左孩子，且为叶子节点，则直接将其删除，令其父节点的左指针为空。
   2. 如果当前节点为左孩子，且存在左右子树，则找到当前节点的后继节点，令其后继节点的值作为其父节点的左孩子的值。
   3. 如果当前节点为右孩子，且为叶子节点，则直接将其删除，令其父节点的右指针为空。
   4. 如果当前节点为右孩子，且存在左右子树，则找到当前节点的后继节点，令其后继节点的值作为其父节点的右孩子的值。
   5. 如果当前节点只存在唯一的一棵子树，无论其是左孩子还是右孩子，处理逻辑都是将其子节点替换当前节点。
2. 如果当前节点值小于要删除的节点值，则有两种情况：
   1. 如果当前节点没有右孩子，则返回false，删除失败。
   2. 否则递归删除右子树。
3. 如果当前节点值大于要删除的节点值，则有两种情况：
   1. 如果当前节点没有左孩子，则返回false，删除失败。
   2. 否则递归删除左子树。

        至此，二叉排序树的增加节点，删除节点，查找节点已全部讲解完毕，下面附上最终代码，并对删除节点做简单的运行。

二叉排序树完整代码

// 二叉排序树的节点
class SBTreeNode[T: Ordering](var value: T) {
  // 从冥界召唤可以比较 T 类型的比较器(Ordering)
  private val orderValueT: Ordering[T] = implicitly[Ordering[T]]
  // 父节点
  var p: SBTreeNode[T] = _
  // 左节点
  var left: SBTreeNode[T] = _
  // 右节点
  var right: SBTreeNode[T] = _

  // 插入节点
  def add(ele: T): Unit = {
    // 如果小于等于当前值, 则在左边添加
    if (orderValueT.lteq(ele, value)) {
      // 如果左节点是 null, 则左节点置为新节点
      if (left == null) {
        left = new SBTreeNode[T](ele)
        left.p = this
      }
      else // 否则递归的在左节点添加节点
        left.add(ele)
    } else { // 否则向右边添加
      if (right == null) {
        right = new SBTreeNode[T](ele)
        right.p = this
      }
      else right.add(ele)
    }
  }

  // 中序遍历节点
  def infixForeach(op: T => Unit): Unit = {
    if (left != null) left.infixForeach(op)
    op(value)
    if (right != null) right.infixForeach(op)
  }

  // 查找节点
  def searchNode(ele: T): SBTreeNode[T] = {
    // 如果小于当前节点, 则去左边查找
    if (orderValueT.lt(ele, value) && left != null)
      left.searchNode(ele)

    // 如果大于当前节点, 则去右边查找
    else if (orderValueT.gt(ele, value) && right != null)
      right.searchNode(ele)

    // 如果和当前节点的值相等, 则返回当前节点
    else if (orderValueT.equiv(ele, value))
      this

    // 如果没有找到, 则返回null
    else null
  }

  // 删除节点
  def deleteSBT(ele: T): Boolean = {
    // 1. 如果当前节点为要删除的节点
    if (orderValueT.equiv(ele, value)) {
      // 由于将当前节点删除后，需要重新指定父节点的孩子节点，所以需要判断当前节点是左孩子还是右孩子
      // 假设当前节点为左孩子
      var isLeft = true
      //判断是否为右孩子
      if (p != null && p.right != null && orderValueT.equiv(p.right.value, ele)) {
        isLeft = false
      }
      // 1.1 如果当前节点为叶子节点
      if (left == null && right == null) {
        // 如果删除的是左孩子，则父节点的左指针指向空
        if (isLeft) p.left = null
        // 否则父节点的右指针指向空
        else p.right = null
      } else if (left != null && right != null) {
        // 1.2 如果当前节点的左右节点都不为空，则找到右子树的最小节点，将其删除，
        // 并将其值替换给当前节点
        value = right.deleteMin
      } else {
        // 1.3 否则当前节点只有一颗子树
        // 找到唯一的子节点
        val onlyNode = if (left != null) left else right
        if (isLeft) p.left = onlyNode
        else p.right = onlyNode
      }
      true
    }

    // 2. 如果要删除的节点比当前节点小
    else if (orderValueT.lt(ele, value)) {
      // 如果左节点为空，删除失败
      if (left == null) false
      // 否则递归删除左子树
      else left.deleteSBT(ele)
    }

    // 3. 否则要删除的节点比当前节点大
    else {
      // 如果右子树为空，则删除失败
      if (right == null) false
      // 否则递归删除右子树
      else right.deleteSBT(ele)
    }
  }

  // 寻找后继节点
  // 删除当前节点的最小节点，并返回最小节点的值域
  def deleteMin: T = {
    var minNode = this
    //遍历左节点, 找到最小的子节点
    while (minNode.left != null) {
      minNode = minNode.left
    }
    // 删除最小的节点
    minNode.deleteSBT(minNode.value)
    //返回最小节点的值域
    minNode.value
  }

  // 重写toString方法
  override def toString: String = s"value= $value \n p= ${p.value}"
}

// 排序二叉树
class SearchBinaryTree[T: Ordering] {
  // 排序二叉树的根节点
  var root: SBTreeNode[T] = _

  // 向排序二叉树中添加节点
  def add(ele: T): Unit = {
    // 如果 root 节点为 null, 则把元素置为 root 位置
    if (root == null)
      root = new SBTreeNode[T](ele)
    // 如果 root 节点不为空则调用 root 的 add 方法来添加元素
    else
      root.add(ele)
  }

  // 中序遍历二叉树
  def infixForeach(op: T => Unit): Unit = {
    if (root == null)
      println("二叉排序树为空！！！")
    else
      root.infixForeach(op)
  }

  // 查找节点
  def searchNode(ele: T): SBTreeNode[T] = {
    if (root == null) null
    else
      root.searchNode(ele)
  }

  // 删除指定节点
  def deleteNode(ele: T): Boolean = {
    // 1.如果根节点为空，返回false
    if (root == null) false
    else if (root.value == ele) { // 2.如果要删除的是根节点
      // 如果根节点是唯一的节点，则直接令root = null
      if (root.left == null && root.right == null) {
        root = null
      } else if (root.left != null && root.right != null) {
        // 如果根节点的左右节点都不为空，则删除右子树的最小节点，并且用右子树的最小值代替根节点
        root.value = root.right.deleteMin
      } else {
        // 如果根节点只有一颗子树，则用子树的节点代替根节点
        root = if (root.left != null) root.left else root.right
      }
      true
    }
    // 3.否则，要删除的就是root的子节点
    else root.deleteSBT(ele)
  }
}

测试结果：

有问题可以一起探讨，希望对你有帮助；

我的一小步，填坑一大步！！！