数据预处理 | 数据标准化及归一化
数据预处理时才发现不清楚是否需要做数据标准化及归一化?也不清楚标准化及归一化标准化及归一化区别在哪?有哪些标准化和归一化的工具和方法?
在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲和数量级。当各指标间的水平相差很大时,如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。因此,为了保证结果的可靠性,需要对原始指标数据进行标准化处理。
数据的标准化或归一化是将数据按比例缩放,使其缩放到相同的数据区间和范围,以减少规模、特征、分布差异等对模型的影响。除了做模型计算,标准化后的数据还具有直接计算并生成复合指标的意义,是加权指标的必要步骤。
本文将一文搞定数据标准化和归一化。从数据标准化及归一化具体含义、区别、实战时常用方法及工具等方面具体介绍数据预处理过程中的数据标准化及归一化。
哪些模型对标准化处理比较敏感
基于距离度量的模型
由于距离对特征之间不同取值范围非常敏感,若某个特征取值非常大而导致其掩盖了特征之间的距离对总距离 的影响,这样距离模型便不能很好地将不同类别的特征区分开。所以基于距离读量的模型是十分有必要做数据标准化处理的,此类模型在归一化后可有可能提高精度。
最典型基于距离度量的模型包括KNN、kmeans聚类、感知机和SVM。
判别模型
有些模型在各个维度进行不均匀伸缩后,最优解与原来不等价,例如SVM。对于这样的模型,除非本来各维数据的分布范围就比较接近,否则必须进行标准化,以免模型参数被分布范围较大或较小的数据占住主导地位。
有些模型在各个维度进行不均匀伸缩后,最优解与原来等价,例如logistic regression。对于这样的模型,是否标准化理论上不会改变最优解。但是,由于实际求解往往使用迭代算法,如果目标函数的形状太"扁",迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型, 最好也进行数据标准化。
通过梯度下降求解最优解的模型
归一化后加快了梯度下降求最优解的速度, 运用梯度下降,损失等高线是椭圆形,需要进行多次迭代才能达到最优点,如果进行归一化了,那么等高线就是圆形的,促使往原点迭代,从而导致需要迭代次数较少。因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。
如GBDT的树是在上一颗树的基础上通过梯度下降求解最优解,归一化能收敛的更快,而随机森林本来就是通过减少方差提高性能的,树之间建立关系是独立的,不需要归一化
概率模型不需要归一化
树模型是通过寻找最优分裂点构成的,样本点的数值缩放不影响分裂点的位置,对树模型的结构也不造成影响,而且树模型不能进行梯度下降,因为树模型是阶跃的,阶跃是不可导的,因此不需要归一化。
决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感。因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率。
归一化和标准化选择
若对输出结果范围有要求 ---- 用归一化
数据较为稳定,不存在极端的最大最小 ---- 用归一化
如果数据存在异常值和较多噪音 ---- 用标准化,可以间接通过中心化避免异常值和极端值的影响
归一化和标准化原因
消除量纲或数值对计算结果的影响
模型要求数据假定服从相应的分布
将数据缩放到指定的区间上
归一化、标准化方法
Z-Score 标准化
一种中心化方法,基于原始数据的均值和标准差进行的标准化。标准化后数据均值为0,方差为1。会改变原有数据结构,不适合对稀疏数据的处理。
语法:
sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)
通过去除平均值和缩放到单位方差来标准化特征。
样本
x的标准分数计算为: 其中 为训练样本的均值,如果with_mean=False则 为0, 为训练样本的标准差,如果with_std=False则 为1。通过计算训练集中样本的相关统计量,独立地对每个特征进行定心和缩放,然后将均值和标准差存储起来,通过变换用于后续的数据。
数据集的标准化是许多机器学习估计器的共同需求:如果单个特征或多或少看起来不像标准正态分布数据 (例如,具有0均值和单位方差的高斯分布数据),它们可能会表现得很糟糕。
例如,在学习算法的目标函数中使用的许多元素(如支持向量机的RBF核或线性模型的
L1和L2正则化器)假设所有特征都以0为中心,并且具有相同顺序的方差。如果某个特性的方差比其他特性大几个数量级,那么它可能会支配目标函数,使估计器无法按照预期正确地从其他特性学习。该scaler也可以应用于稀疏的CSR或CSC矩阵,通过传递with_mean=False来避免破坏数据的稀疏结构。
例:
>>> from sklearn.preprocessing import StandardScaler
>>> data = [[0, 0], [0, 0], [1, 1], [1, 1]]
>>> scaler = StandardScaler()
>>> print(scaler.fit(data))
StandardScaler()
>>> print(scaler.mean_)
[0.5 0.5]
>>> print(scaler.transform(data))
[[-1. -1.]
[-1. -1.]
[ 1. 1.]
[ 1. 1.]]
>>> print(scaler.transform([[2, 2]]))
[[3. 3.]]
Max-Min 归一化
一种线性变换方法,标准化后数据完全落入[0,1]区间,能够较好的保持原有数据结构。
语法:
sklearn.preprocessing.minmax_scale(X, feature_range=(0, 1), *, axis=0, copy=True)
变换特征,通过缩放每个特征到一个给定的范围。
该估计器对每个特征分别进行缩放和转换,使其在训练集中的给定范围内,例如在0到1之间。
例:
>>> from sklearn.preprocessing import MinMaxScaler
>>> data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
>>> scaler = MinMaxScaler()
>>> print(scaler.fit(data))
MinMaxScaler()
>>> print(scaler.data_max_)
[ 1. 18.]
>>> print(scaler.transform(data))
[[0. 0. ]
[0.25 0.25]
[0.5 0.5 ]
[1. 1. ]]
>>> print(scaler.transform([[2, 2]]))
[[1.5 0. ]]
Max-Abs 用于稀疏数据
最大值绝对值标准化,标准化后数据落入[-1,1]区间。
语法:
sklearn.preprocessing.maxabs_scale(X, *, axis=0, copy=True)
例:
>>> from sklearn.preprocessing import MaxAbsScaler
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> transformer = MaxAbsScaler().fit(X)
>>> transformer
MaxAbsScaler()
>>> transformer.transform(X)
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
按其最大绝对值缩放每个特征。
该估计器对每个特征分别进行缩放和转换,这样训练集中每个特征的最大绝对值将为1.0。它不会移动/中心数据,因此不会破坏任何稀疏性。
这个标量器也可以应用于稀疏CSR或CSC矩阵。
RobustScalar 针对离群点
Robust ---- This Scaler removes the median and scales the data according to the quantile range.
Huber从稳健统计的角度系统地给出了鲁棒性3个层面的概念:
模型具有较高的精度或有效性,这也是对于机器学习中所有学习模型的基本要求;
对于模型假设出现的较小偏差,主要是噪声(
noise),只能对算法性能产生较小的影响;对于模型假设出现的较大偏差,主要是离群点(
outlier),不可对算法性能产生"灾难性"的影响。
在机器学习,训练模型时,工程师可能会向算法内添加噪声(如对抗训练),以便测试算法的鲁棒性。可以将此处的鲁棒性理解为算法对数据变化的容忍度有多高。鲁棒性并不同于稳定性,稳定性通常意味着特性随时间不变化的能力,鲁棒性则常被用来描述可以面对复杂适应系统的能力,需要更全面的对系统进行考虑。
异常点在普通标准化后会失去离群特征。该方法对数据中心化和数据的鲁棒性更强的参数控制。
语法:
sklearn.preprocessing.RobustScaler(*, with_centering=True, with_scaling=True, quantile_range=(25.0, 75.0), copy=True)
使用对异常值稳健性的统计数据来衡量特征。
这个标量去除中值,并根据分位数范围(默认为IQR:四分位数范围)对数据进行缩放。IQR是第1个四分位数(第25分位数)和第3个四分位数(第75分位数)之间的范围。
通过计算训练集中样本的相关统计量,独立地对每个特征进行定心和缩放。然后存储中值和四分位范围,使用变换方法对以后的数据进行处理。
数据集的标准化是许多机器学习估计器的常见需求。这通常是通过去除平均值和缩放到单位方差来实现的。然而,异常值往往会对样本均值/方差产生负面影响。在这种情况下,中位数和四分位范围通常会给出更好的结果。
例:
>>> from sklearn.preprocessing import RobustScaler
>>> X = [[ 1., -2., 2.],
... [ -2., 1., 3.],
... [ 4., 1., -2.]]
>>> transformer = RobustScaler().fit(X)
>>> transformer
RobustScaler()
>>> transformer.transform(X)
array([[ 0. , -2. , 0. ],
[-1. , 0. , 0.4],
[ 1. , 0. , -1.6]])
Normalizer 用于文本分类
将输入缩放到单元规范是文本分类或聚类的常见操作。例如,两个l2-归一化后的TF-IDF向量的点积是向量的余弦相似度,是信息检索界常用的向量空间模型的基本相似度度量。
语法:
sklearn.preprocessing.Normalizer(norm='l2', *, copy=True)
例:
>>> from sklearn.preprocessing import Normalizer
>>> X = [[4, 1, 2, 2],
... [1, 3, 9, 3],
... [5, 7, 5, 1]]
>>> transformer = Normalizer().fit(X) # fit does nothing.
>>> transformer
Normalizer()
>>> transformer.transform(X)
array([[0.8, 0.2, 0.4, 0.4],
[0.1, 0.3, 0.9, 0.3],
[0.5, 0.7, 0.5, 0.1]])
log 函数转换
通过以10为底的 函数转换的方法同样可以通过 实现归一化,但是要是需要数据一定落到[0,1]区间上,应该还要除以,max为样本数据最大值,并且所有的数据都要大于等于1。
atan 函数转换
反余切函数转换,公式如下:
用反正切函数也可以实现数据的归一化,使用这个方法需要注意的是如果想映射的区间为[0,1],则数据都应该大于等于0,小于0的数据将被映射到[-1,0]区间上。
更多预处理参见
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.preprocessing
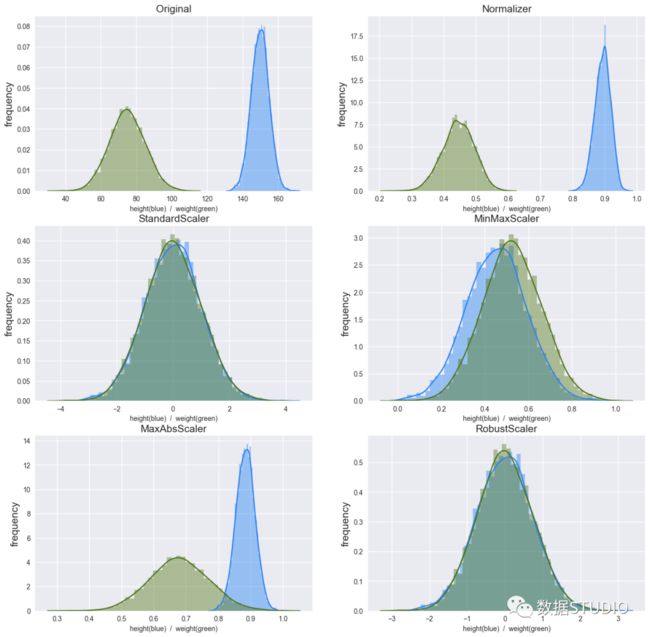
实例
各个标准化结果对比。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler, MinMaxScaler, MaxAbsScaler, Normalizer, RobustScaler
plt.style.use('seaborn')
def plot(data, title):
plt.ylabel('frequency', fontdict={'fontsize':15})
plt.xlabel('height(blue) / weight(green)', fontdict={'fontsize':10})
plt.title(title, fontdict={'fontsize':15})
sns.distplot(data[:, 0:1], color='#0080ff')
sns.distplot(data[:, 1:2], color='#407600')
np.random.seed(42)
height = np.random.normal(loc=150, scale=5, size=5000).reshape(-1, 1)
weight = np.random.normal(loc=75, scale=10, size=5000).reshape(-1, 1)
original_data = np.concatenate((height, weight), axis=1)
class_name = [Normalizer(), StandardScaler(), MinMaxScaler(), MaxAbsScaler(), RobustScaler()]
title_name = ['Normalizer', 'StandardScaler', 'MinMaxScaler', 'MaxAbsScaler', 'RobustScaler']
plt.figure(figsize=(16,16), dpi=100)
for i in range(1,7):
if i == 1:
plt.subplot(3,2,1)
plot(original_data, 'Original')
else:
plt.subplot(3,2,i)
plot(class_name[i-2].fit_transform(original_data), title_name[i-2])
plt.show()
plt.savefig('Standard.png')
输出结果:
三连、在看支持哦~