Pytorch深度学习（二）：反馈神经网络（BPNN）

Pytorch深度学习（二）：反馈神经网络（BPNN）

• 参考B站课程：《PyTorch深度学习实践》完结合集
• 传送门：《PyTorch深度学习实践》完结合集

本文浅学反馈神经网络（Back Propagation Neural Network）

一、反向传播（Back Propagation）

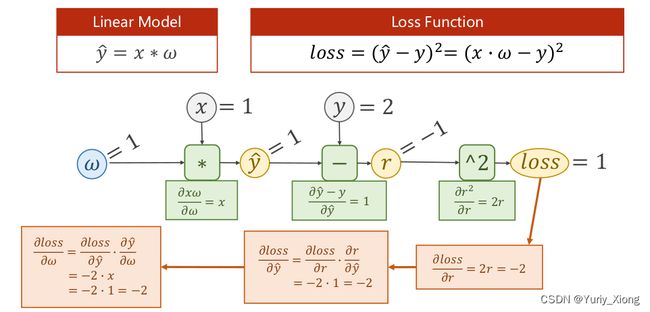
仍然以上文的线性模型为例子，其第一次“学习”过程如下：

其中，反向传播过程求出了误差 $loss$ 关于各个变量的偏导数值，最后用于更新权重 $w$ ，而这一过程，我们利用torch中的函数来实现。关键代码：l.backward()

相关预备知识：

• 什么是张量
• torch.Tensor的数据类型
• w.grad.data的数据类型
• w.grad.data.item()的数据类型
• …
  读者自行了解或利用type()等进行程序实验

程序如下：

import torch
import numpy as np
from matplotlib import pyplot as plt

xdata = [1, 2, 3]
ydata = [2, 4, 6]

w = torch.Tensor([1])
w.requires_grad = True  # the default is False which will don't compute grad


costlist = []


def forward(x):
    return x * w

def loss(x, y):
    ypred = forward(x)
    return (ypred - y) ** 2



print('predict (before training)', 4, forward(4).item())

for epoch in range(100):
    cost = 0
    for x, y in zip(xdata, ydata):
        l = loss(x, y)
        l.backward()    # compute w.grad = \frac{\partial l}{\partial w}
        cost += l.item()
        print('\t grad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data

        w.grad.data.zero_()
    costlist.append(cost/len(xdata))
    print('progress:', epoch, l.item())

print('predict (after training)', 4, forward(4).item())

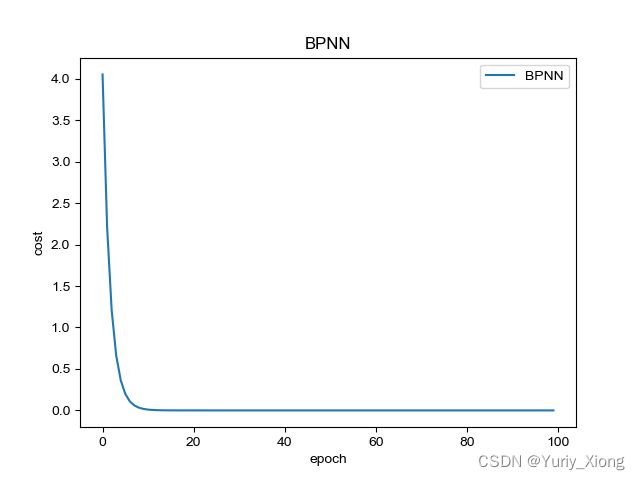
plt.plot(range(100), costlist, label='BPNN')
plt.xlabel('epoch')
plt.ylabel('cost')
plt.title('BPNN')
plt.legend()
plt.show()

可见，随着迭代步数的增加，误差快速减小，结果是可靠的

二、练习

将线性模型改为以下一元二次多项式的模型，同样通过BPNN求出相关的参数 $w_1,w_2,b$ ，并且预测 $x=4$ 时 $y$ 的值

import torch
import numpy as np
from matplotlib import pyplot as plt

xdata = [1, 2, 3]
ydata = [2, 4, 6]

w1 = torch.Tensor([1])
w1.requires_grad = True  # the default is False which will don't compute grad

w2 = torch.Tensor([1])
w2.requires_grad = True  # the default is False which will don't compute grad

b = torch.Tensor([1])
b.requires_grad = True  # the default is False which will don't compute grad

costlist = []

def forward(x):
    return w1 * x**2 + w2 * x + b

def loss(x, y):
    ypred = forward(x)
    return (ypred - y) ** 2


print('predict (before training):', 4, forward(4).item())

for epoch in range(100):
    cost = 0
    for x, y in zip(xdata, ydata):
        l = loss(x, y)
        l.backward()    # compute w.grad = \frac{\partial l}{\partial w}
        cost += l.item()
        print('\t grad:', x, y, w1.grad.item(), w2.grad.item(), b.grad.item())
        w1.data = w1.data - 0.01 * w1.grad.data 
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_() 
    costlist.append(cost/len(xdata))
    print('progress:', epoch, l.item())

print('predict (after training):', 4, forward(4).item())
print('parameter:w1 = {}, w2 = {}, b = {}'.format(w1.item(), w2.item(), b.item()))

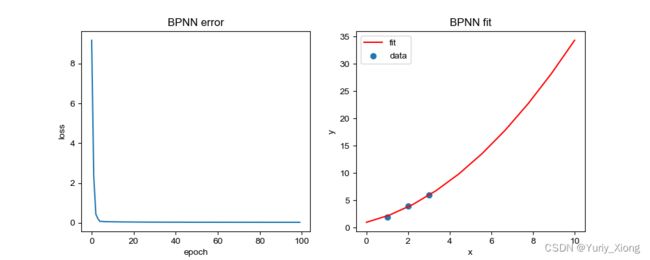
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.plot(range(100), costlist)
plt.xlabel('epoch')
plt.ylabel('loss')

plt.title('BPNN error')

plt.subplot(1, 2, 2)
xx = np.linspace(0, 10, 10)
yy = w1.item()* xx**2 + w2.item()*xx +b.item()
plt.plot(xx, yy, color='red', label='fit')
plt.scatter(xdata, ydata, label='data')
plt.legend()
plt.title('BPNN fit')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

最后一次 “学习” 的结果及相关参数和预测结果：

progress: 99 0.00631808303296566
predict (after training): 4 8.544171333312988
parameter:w1 = 0.24038191139698029, w2 = 0.9266766309738159, b = 0.99135422706604