吴恩达深度学习课程笔记
目录
-
- 通用符号总结
-
- 激活函数sigmoid
- 1、Logistic回归
- 2、梯度下降法
- 3、Logistic回归的梯度下降算法
-
- 3.1假设只有一个训练样本 ( x , y ) (x,y) (x,y)
- 3.2假设有m个训练样本:
- 3.3向量化
- 3.4广播
- 4、 神经网络
- 5、激活函数
-
- 5.1 常用激活函数
- 5.2 经验
- 5.3 为什么要用激活函数
- 6、神经网络的梯度下降法
-
- 参数:
- cost function:
- 正向传播:
- 反向传播:
- 随机初始化
- 7、深层神经网络
-
- 7.1 核对矩阵的维数
- 7.2 前向和反向传播
通用符号总结
| 符号 | 含义 |
|---|---|
| m m m | 训练集规模(样本数量) |
| ( x , y ) , x ∈ R n x , y ∈ { 0 , 1 } (x,y),x\in \mathbb{R}^{nx},y\in\{0,1\} (x,y),x∈Rnx,y∈{0,1} | 样本 |
| x ∈ R n x x\in \mathbb{R}^{nx} x∈Rnx | 表示 x x x是 n x × 1 nx\times1 nx×1维矩阵 |
| R \mathbb{R} R | 实数 |
| x ( i ) x^{(i)} x(i) | 第 i i i个样本 |
| X = [ ∣ ∣ ∣ ∣ x ( 1 ) x ( 2 ) … x ( m ) ∣ ∣ ∣ ∣ ] , X ∈ R n x × m X= \left[ \begin{array}{} | & | & | & |\\\\ x^{(1)} & x^{(2)}& \dots & x^{(m)} \\\\ | & | & | & |\\\\ \end{array}\right], X\in \mathbb{R}^{nx\times m} X=⎣ ⎡∣x(1)∣∣x(2)∣∣…∣∣x(m)∣⎦ ⎤,X∈Rnx×m | 纵向排列,约定俗成的排列方式 |
| Y = [ y ( 1 ) y ( 2 ) … y ( m ) ] , Y ∈ R 1 × m Y= \left[ \begin{array}{} y^{(1)} & y^{(2)} & \dots &y^{(m)} \end{array}\right], Y\in \mathbb{R}^{1 \times m} Y=[y(1)y(2)…y(m)],Y∈R1×m | 纵向排列,约定俗成的排列方式 |
| y ^ \hat{y} y^ | 对 y y y的预测值 |
| w ∈ R n x × 1 , b ∈ R w\in \mathbb{R}^{nx\times1},b\in \mathbb{R} w∈Rnx×1,b∈R | 逻辑回归参数 |
| α \alpha α | 学习率 |
| : = := := | 更新 |
| d J ( w , b ) d b \frac{\mathrm {d} \mathcal{J}(w,b)}{\mathrm {d}b} dbdJ(w,b) | 对 b b b求导,在python中通常使用表示db此变量 |
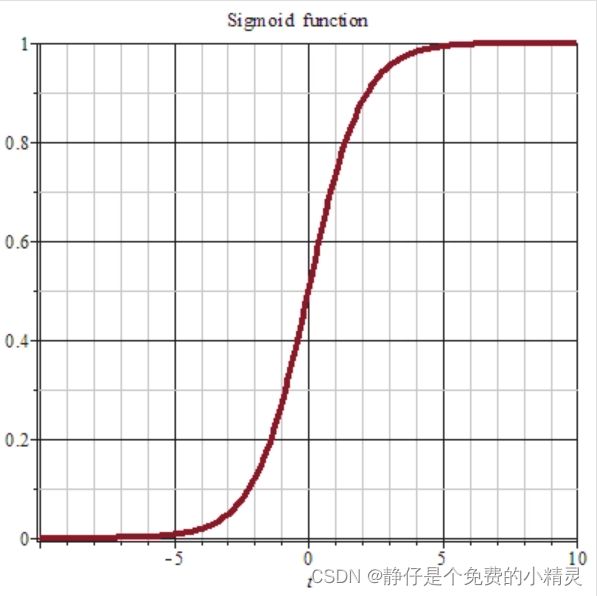
激活函数sigmoid
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
1、Logistic回归
作用:在监督学习下解决二分类问题
y ^ = σ ( w T x + b ) \hat{y}=\sigma(w^Tx+b) y^=σ(wTx+b)
目标: 学习 w w w和 b b b
Logistic回归loss function: L ( y ^ , y ) = − ( y log y ^ + ( 1 − y ) log ( 1 − y ^ ) ) \mathcal{L}(\hat{y},y)=-(y\log \hat{y}+(1-y)\log (1-\hat{y})) L(y^,y)=−(ylogy^+(1−y)log(1−y^))
Logistic回归cost function: J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ i , y i ) \mathcal{J}(w,b)=\frac{1}{m}\sum\limits_{i=1}^{m}\mathcal{L}(\hat{y}^i,y^i) J(w,b)=m1i=1∑mL(y^i,yi)
Loss function :用于衡量在单个训练样本上的表现
Cost function:用于衡量在全体训练样本上的表现
2、梯度下降法
J ( w , b ) \mathcal{J}(w,b) J(w,b)
w : = w − α d J ( w , b ) d w w:=w-\alpha\frac{\mathrm {d} \mathcal{J}(w,b)}{\mathrm {d}w} w:=w−αdwdJ(w,b)
b : = b − α d J ( w , b ) d b b:=b-\alpha\frac{\mathrm {d} \mathcal{J}(w,b)}{\mathrm {d}b} b:=b−αdbdJ(w,b)
α \alpha α表示学习率
3、Logistic回归的梯度下降算法
z = w T x + b z=w^Tx+b z=wTx+b
y ^ = a = σ ( z ) \hat{y}=a=\sigma(z) y^=a=σ(z)
L ( a , y ) = − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) \mathcal{L}(a,y)=-(y\log (a)+(1-y)\log (1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))
3.1假设只有一个训练样本 ( x , y ) (x,y) (x,y)
x = [ x 1 x 2 ] x= \left[ \begin{array}{} x_1\\ x_2 \\ \end{array}\right] x=[x1x2] , w = [ w 1 w 2 ] w= \left[ \begin{array}{} w_1\\ w_2 \\ \end{array}\right] w=[w1w2]
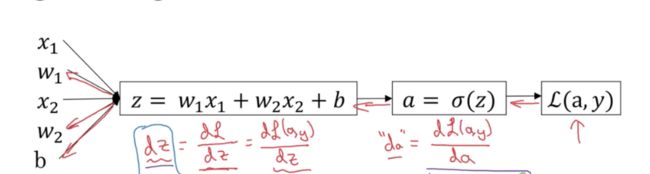
以下给出计算过程:
da= d L ( a , y ) d a = d [ − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) ] d a = d [ − ( y ln ( a ) + ( 1 − y ) ln ( 1 − a ) ) ] d a = − a y + 1 − y 1 − a \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}a}=\frac{\mathrm{d}[-(y\log (a)+(1-y)\log (1-a))]}{\mathrm{d}a}=\frac{\mathrm{d}[-(y\ln (a)+(1-y)\ln(1-a))]}{\mathrm{d}a}=-\frac{a}{y}+\frac{1-y}{1-a} dadL(a,y)=dad[−(ylog(a)+(1−y)log(1−a))]=dad[−(yln(a)+(1−y)ln(1−a))]=−ya+1−a1−y
dz= d L ( a , y ) d z = d L ( a , y ) d a d a d z = d [ 1 1 + e − z ] d z × ( − a y + 1 − y 1 − a ) = e − z ( 1 + e − z ) 2 = ( 1 − a ) × a × ( − a y + 1 − y 1 − a ) = a − y \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}z}=\frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}a}\frac{\mathrm{d}a}{\mathrm{d}z}=\frac{\mathrm{d}[\frac{1}{1+e^{-z}}]}{\mathrm{d}z}\times (-\frac{a}{y}+\frac{1-y}{1-a})=\frac{e^{-z}}{(1+e^{-z})^2}=(1-a)\times a\times (-\frac{a}{y}+\frac{1-y}{1-a})=a-y dzdL(a,y)=dadL(a,y)dzda=dzd[1+e−z1]×(−ya+1−a1−y)=(1+e−z)2e−z=(1−a)×a×(−ya+1−a1−y)=a−y
还记得我们的目标吗?我们的目标是!求 w w w和 b b b!
dw1= d L ( a , y ) d w 1 \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}w_1} dw1dL(a,y)= d L ( a , y ) d a d a d z d z d w 1 \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}a}\frac{\mathrm{d}a}{\mathrm{d}z}\frac{\mathrm{d}z}{\mathrm{d}w_1} dadL(a,y)dzdadw1dz=dz x 1 x_1 x1= x 1 ( a − y ) x_1(a-y) x1(a−y)
dw2= d L ( a , y ) d w 2 \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}w_2} dw2dL(a,y)= d L ( a , y ) d a d a d z d z d w 2 \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}a}\frac{\mathrm{d}a}{\mathrm{d}z}\frac{\mathrm{d}z}{\mathrm{d}w_2} dadL(a,y)dzdadw2dz=dz x 2 x_2 x2= x 2 ( a − y ) x_2(a-y) x2(a−y)
db= d L ( a , y ) d b d a d z d z d b \frac{\mathrm{d}\mathcal{L}(a,y)}{\mathrm{d}b}\frac{\mathrm{d}a}{\mathrm{d}z}\frac{\mathrm{d}z}{\mathrm{d}b} dbdL(a,y)dzdadbdz=dz= a − y a-y a−y
ps:这里的 l o g ( a ) log(a) log(a)就是 l n a lna lna的意思,估计老师习惯使用python中的代码表达方式?
梯度下降:
w 1 : = w 1 − α w_1:=w_1-\alpha w1:=w1−αdw1
w 2 : = w 2 − α w_2:=w_2-\alpha w2:=w2−αdw2
b : = b − α b:=b-\alpha b:=b−αdb
3.2假设有m个训练样本:
首先,让我们时刻记住有关于成本函数 J ( w , b ) \mathcal{J}(w,b) J(w,b)的定义:
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ i , y i ) \mathcal{J}(w,b)=\frac{1}{m}\sum\limits_{i=1}^{m}\mathcal{L}(\hat{y}^i,y^i) J(w,b)=m1i=1∑mL(y^i,yi)
还记得我们的目标吗?我们的目标是!求 w w w和 b b b!
此时
dw1= d J ( a , y ) d w 1 \frac{\mathrm{d}\mathcal{J}(a,y)}{\mathrm{d}w_1} dw1dJ(a,y) , dw2= d J ( a , y ) d w 2 \frac{\mathrm{d}\mathcal{J}(a,y)}{\mathrm{d}w_2} dw2dJ(a,y) , db= d J ( a , y ) d b \frac{\mathrm{d}\mathcal{J}(a,y)}{\mathrm{d}b} dbdJ(a,y)
那么在算法中应该如何实现呢?伪代码如下所示:
J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
3.3向量化
在上面的伪代码中我们可以看到,需要很多很多for循环才可以实现训练,但是显式地使用for循环的时间开销很大,在实际的代码编写中应尽量使用向量化的代码,可以极大减少时间开销。
链接: numpy的参考文档
向量化的逻辑回归实现:
假设有 m m m个样本:
此时 X = [ ∣ ∣ ∣ ∣ x ( 1 ) x ( 2 ) … x ( m ) ∣ ∣ ∣ ∣ ] , X ∈ R n x × m X= \left[ \begin{array}{} | & | & | & |\\\\ x^{(1)} & x^{(2)}& \dots & x^{(m)} \\\\ | & | & | & |\\\\ \end{array}\right], X\in \mathbb{R}^{nx\times m} X=⎣ ⎡∣x(1)∣∣x(2)∣∣…∣∣x(m)∣⎦ ⎤,X∈Rnx×m
Y = [ y ( 1 ) y ( 2 ) … y ( m ) ] , Y ∈ R 1 × m Y= \left[ \begin{array}{} y^{(1)} & y^{(2)} & \dots &y^{(m)} \end{array}\right], Y\in \mathbb{R}^{1 \times m} Y=[y(1)y(2)…y(m)],Y∈R1×m
Z = [ z ( 1 ) z ( 2 ) … z ( m ) ] , Z ∈ R 1 × n x Z= \left[ \begin{array}{} z^{(1)} & z^{(2)} & \dots &z^{(m)} \end{array}\right], Z\in \mathbb{R}^{1\times nx} Z=[z(1)z(2)…z(m)],Z∈R1×nx
w ∈ R n x × 1 , b ∈ R w\in \mathbb{R}^{nx\times 1},b\in \mathbb{R} w∈Rnx×1,b∈R
B = [ b , b , … , b ] , B ∈ R 1 × m B=[b,b,\dots,b],B\in\mathbb{R}^{1\times m} B=[b,b,…,b],B∈R1×m
此时逻辑回归写作:
Z = w T X + B Z=w^TX+B Z=wTX+B
A = σ ( Z ) A=\sigma(Z) A=σ(Z)
d z = A − Y \mathrm{d}z= A-Y dz=A−Y
d w = 1 m × X × d z T \mathrm{d}w=\frac{1}{m}\times X\times \mathrm{d}z^T dw=m1×X×dzT
d b = 1 m ∑ i = 1 m d z ( i ) \mathrm{d}b=\frac{1}{m}\sum\limits_{i=1}^{m}\mathrm{d}z^{(i)} db=m1i=1∑mdz(i)
更新:
w : = w − α d w w:=w-\alpha \mathrm{d}w w:=w−αdw
b : = b − α d b b:=b-\alpha \mathrm{d}b b:=b−αdb
代码写作:
for iter in range(1000):\\1000次梯度下降
Z=np.dot(w.T,X)+b
A=sigmoid(Z)
dZ=A-Y
dw=np.dot(X,dZ.T)/m
db=np.sum(dZ)/m
3.4广播
播提供了一种向量化数组操作的方法,是重要的NumPy抽象
使用广播替代显示的for循环可以减少代码运行时间
链接: numpy广播
广播操作的注意事项:
- 用矩阵不要用数组
也就是不要用np.random.randn(3),而是用np.random.randn(3,1) - 尽量用列向量
也就是不要用np.random.randn(1,3),而是用np.random.randn(3,1) - 使用
.shap,.assert,.reshap来确保矩阵形状
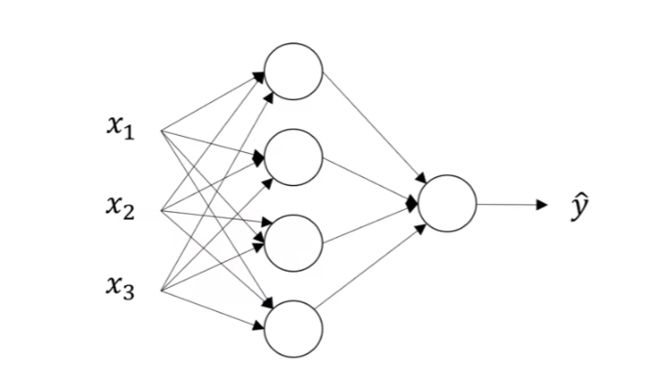
4、 神经网络
这是一个简单的神经网络示意图,只有一个训练样本。
一个圈圈表示:

其中:
x 1 x_1 x1是一个数, w 1 w_1 w1是一个数
x = [ x 1 x 2 x 3 ] ∈ R 3 × 1 x= \left[ \begin{array}{} x_1 \\ x_2 \\ x_3\\ \end{array}\right] \in \mathbb{R}^{3\times 1} x=⎣ ⎡x1x2x3⎦ ⎤∈R3×1, w 1 [ 1 ] = [ x 1 x 2 x 3 ] ∈ R 3 × 1 w_1^{[1]}= \left[ \begin{array}{} x_1 \\ x_2 \\ x_3\\ \end{array}\right] \in \mathbb{R}^{3\times 1} w1[1]=⎣ ⎡x1x2x3⎦ ⎤∈R3×1
z i [ j ] z_i^{[j]} zi[j]上面的j表示所在层数,下面的i表示是该层的第几个节点
w [ 1 ] = [ w 1 [ 1 ] T w 2 [ 1 ] T w 3 [ 1 ] T w 4 [ 1 ] T ] ∈ R 4 × 3 w^{[1]}=\left[ \begin{array}{} w_1^{[1]T} \\ w_2^{[1]T} \\ w_3^{[1]T}\\ w_4^{[1]T}\\ \end{array}\right] \in \mathbb{R}^{4\times 3} w[1]=⎣ ⎡w1[1]Tw2[1]Tw3[1]Tw4[1]T⎦ ⎤∈R4×3
b [ 1 ] = [ b 1 [ 1 ] T b 2 [ 1 ] T b 3 [ 1 ] T b 4 [ 1 ] T ] ∈ R 4 × 1 b^{[1]}=\left[ \begin{array}{} b_1^{[1]T} \\ b_2^{[1]T} \\ b_3^{[1]T}\\ b_4^{[1]T}\\ \end{array}\right] \in \mathbb{R}^{4\times 1} b[1]=⎣ ⎡b1[1]Tb2[1]Tb3[1]Tb4[1]T⎦ ⎤∈R4×1
a [ 1 ] = [ a 1 [ 1 ] T a 2 [ 1 ] T a 3 [ 1 ] T a 4 [ 1 ] T ] ∈ R 4 × 1 a^{[1]}=\left[ \begin{array}{} a_1^{[1]T} \\ a_2^{[1]T} \\ a_3^{[1]T}\\ a_4^{[1]T}\\ \end{array}\right] \in \mathbb{R}^{4\times 1} a[1]=⎣ ⎡a1[1]Ta2[1]Ta3[1]Ta4[1]T⎦ ⎤∈R4×1
z [ 1 ] = [ b 1 [ 1 ] T b 2 [ 1 ] T b 3 [ 1 ] T b 4 [ 1 ] T ] ∈ R 4 × 1 z^{[1]}=\left[ \begin{array}{} b_1^{[1]T} \\ b_2^{[1]T} \\ b_3^{[1]T}\\ b_4^{[1]T}\\ \end{array}\right] \in \mathbb{R}^{4\times 1} z[1]=⎣ ⎡b1[1]Tb2[1]Tb3[1]Tb4[1]T⎦ ⎤∈R4×1
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z_1^{[1]}=w_1^{[1]T}x+b_1^{[1]},a_1^{[1]}=\sigma(z_1^{[1]}) z1[1]=w1[1]Tx+b1[1],a1[1]=σ(z1[1])
z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) z_2^{[1]}=w_2^{[1]T}x+b_2^{[1]},a_2^{[1]}=\sigma(z_2^{[1]}) z2[1]=w2[1]Tx+b2[1],a2[1]=σ(z2[1])
z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] ) z_3^{[1]}=w_3^{[1]T}x+b_3^{[1]},a_3^{[1]}=\sigma(z_3^{[1]}) z3[1]=w3[1]Tx+b3[1],a3[1]=σ(z3[1])
z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] ) z_4^{[1]}=w_4^{[1]T}x+b_4^{[1]},a_4^{[1]}=\sigma(z_4^{[1]}) z4[1]=w4[1]Tx+b4[1],a4[1]=σ(z4[1])
由此可以推出:
z [ 1 ] = w [ 1 ] x + b [ 1 ] z^{[1]}=w^{[1]}x+b^{[1]} z[1]=w[1]x+b[1]
a [ 1 ] = σ ( z [ 1 ] ) a^{[1]}=\sigma(z^{[1]}) a[1]=σ(z[1])
z [ 2 ] = w [ 2 ] a [ 2 ] + b [ 2 ] z^{[2]}=w^{[2]}a^{[2]}+b^{[2]} z[2]=w[2]a[2]+b[2]
a [ 2 ] = σ ( z [ 2 ] ) a^{[2]}=\sigma(z^{[2]}) a[2]=σ(z[2])
当有多个 m m m的时候
Z [ 1 ] = w [ 1 ] X + b [ 1 ] Z^{[1]}=w^{[1]}X+b^{[1]} Z[1]=w[1]X+b[1]
其中
X = [ x [ 1 ] , x [ 2 ] , … , x [ m ] ] ∈ R 3 × m X=[x^{[1]},x^{[2]},\dots,x^{[m]}] \in \mathbb{R}^{3\times m} X=[x[1],x[2],…,x[m]]∈R3×m
Z [ 1 ] = [ z [ 1 ] ( 1 ) , z [ 1 ] ( 2 ) , … , z [ 1 ] ( m ) ] ∈ R 4 × m Z^{[1]}=[z^{[1](1)},z^{[1](2)},\dots,z^{[1](m)}] \in \mathbb{R}^{4\times m} Z[1]=[z[1](1),z[1](2),…,z[1](m)]∈R4×m
z [ i ] ( j ) z^{[i](j)} z[i](j)表示第i层第j个样本
A [ 1 ] = [ a [ 1 ] ( 1 ) , a [ 1 ] ( 2 ) , … , a [ 1 ] ( m ) ] ∈ R 4 × m A^{[1]}=[a^{[1](1)},a^{[1](2)},\dots,a^{[1](m)}] \in \mathbb{R}^{4\times m} A[1]=[a[1](1),a[1](2),…,a[1](m)]∈R4×m
由此可以推出
Z [ 1 ] = w [ 1 ] X + b [ 1 ] Z^{[1]}=w^{[1]}X+b^{[1]} Z[1]=w[1]X+b[1]
A [ 1 ] = g [ 1 ] ( Z [ 1 ] ) A^{[1]}=g^{[1]}(Z^{[1]}) A[1]=g[1](Z[1])
Z [ 2 ] = w [ 2 ] X + b [ 2 ] Z^{[2]}=w^{[2]}X+b^{[2]} Z[2]=w[2]X+b[2]
A [ 2 ] = g [ 2 ] ( Z [ 2 ] ) = σ ( Z [ 2 ] ) A^{[2]}=g^{[2]}(Z^{[2]})=\sigma(Z^{[2]}) A[2]=g[2](Z[2])=σ(Z[2])
5、激活函数
5.1 常用激活函数
sigmoid : σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1
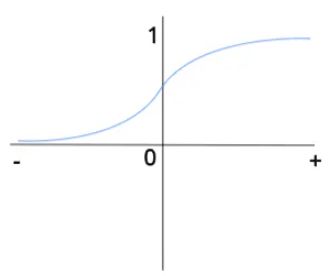
tanh: t a n h ( z ) = e z − e − z e z + e − z tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} tanh(z)=ez+e−zez−e−z
tanh就是sigmoid的平移,比起后者有数据中心化的优点
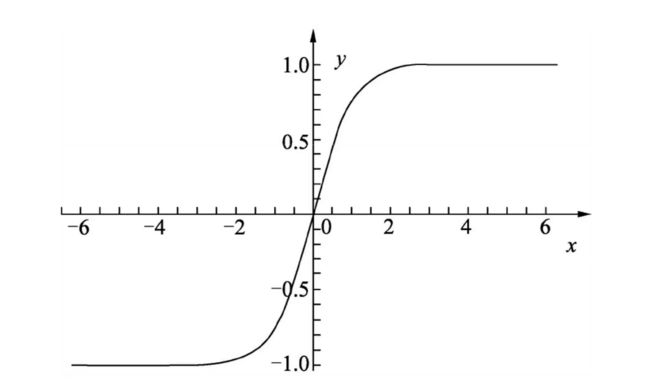
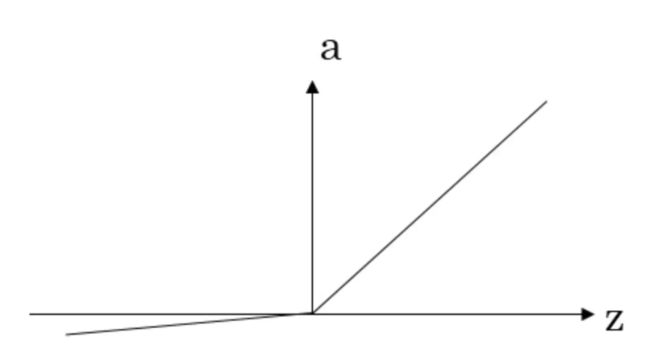
Relu : R e l u ( z ) = m a x ( 0 , z ) Relu(z)=max(0,z) Relu(z)=max(0,z)

Leaky Relu : L e a k y R e l u ( z ) = m a x ( 0.01 z , z ) LeakyRelu(z)=max(0.01z,z) LeakyRelu(z)=max(0.01z,z)
这个0.01的值可以是任意较小的值
5.2 经验
经验:
1、隐藏层用tanh或relu,别用sigmoid,输出层用sigmoid(因为输出的标签一般在0~1之间)
2、但在实际的实验中还是都试试,哪个效果好用哪个
5.3 为什么要用激活函数
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机。
补充:为什么要随机初始化,不随机初始化则同一层的每个节点的计算结果都相同,那么有很多的节点就没有意义。
6、神经网络的梯度下降法
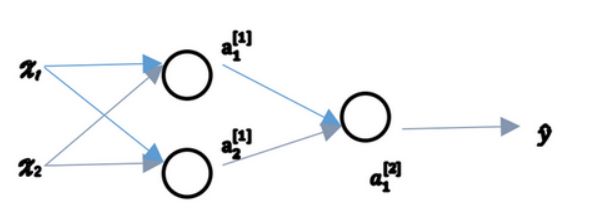
以两层神经网络举例:
参数:
输入特征: n [ 0 ] = n x 个 n^{[0]}=nx个 n[0]=nx个
隐藏单元: n [ 1 ] n^{[1]} n[1]个
输出单元: n [ 2 ] n^{[2]} n[2]个
w [ 1 ] ∈ R n [ 1 ] × n [ 0 ] w^{[1]}\in\mathbb{R}^{n^{[1]}\times n^{[0]}} w[1]∈Rn[1]×n[0]
b [ 1 ] ∈ R n [ 1 ] × 1 b^{[1]}\in\mathbb{R}^{n^{[1]}\times 1} b[1]∈Rn[1]×1
w [ 2 ] ∈ R n [ 2 ] × n [ 1 ] w^{[2]}\in\mathbb{R}^{n^{[2]}\times n^{[1]}} w[2]∈Rn[2]×n[1]
b [ 2 ] ∈ R n [ 2 ] × 1 b^{[2]}\in\mathbb{R}^{n^{[2]}\times 1} b[2]∈Rn[2]×1
y ^ = a [ 2 ] \hat{y}=a^{[2]} y^=a[2]
cost function:
J = ( w [ 1 ] , b [ 1 ] , w [ 2 ] , b [ 2 ] ) = 1 m ∑ i = 1 m ( y ^ , y ) J=(w^{[1]},b^{[1]},w^{[2]},b^{[2]})=\frac{1}{m}\sum\limits_{i=1}^{m}(\hat{y},y) J=(w[1],b[1],w[2],b[2])=m1i=1∑m(y^,y)
正向传播:
Z [ 1 ] = w [ 1 ] X + b [ 1 ] Z^{[1]}=w^{[1]}X+b^{[1]} Z[1]=w[1]X+b[1]阿萨
A [ 1 ] = g [ 1 ] ( Z [ 1 ] ) A^{[1]}=g^{[1]}(Z^{[1]}) A[1]=g[1](Z[1])
Z [ 2123234556789897 / ∗ / ∗ 12345678454556235678856123564879787 ] = w [ 2 ] X + b [ 2 ] Z^{[2123234556789897/*/*12345678454556235678856123564879787]}=w^{[2]}X+b^{[2]} Z[2123234556789897/∗/∗12345678454556235678856123564879787]=w[2]X+b[2]
A [ 2 ] = g [ 2 ] ( Z [ 2 ] ) = σ ( Z [ 2 ] ) A^{[2]}=g^{[2]}(Z^{[2]})=\sigma(Z^{[2]}) A[2]=g[2](Z[2])=σ(Z[2])
反向传播:
d z [ 2 ] = A [ 2 ] − Y dz^{[2]}=A^{[2]}-Y dz[2]=A[2]−Y
d w [ 2 ] = 1 m d z [ 2 ] A [ 1 ] T dw^{[2]}=\frac{1}{m}dz^{[2]}A^{[1]T} dw[2]=m1dz[2]A[1]T
d b [ 2 ] = 1 m db^{[2]}=\frac{1}{m} db[2]=m1np.sum( d z [ 2 ] dz^{[2]} dz[2],axis=1,keepdims=True)
d z [ 1 ] = W [ 2 ] T d z [ 2 ] × g [ 1 ] ′ ( z [ 1 ] ) dz^{[1]}=W^{[2]T}dz^{[2]}\times g^{[1]'}(z^{[1]}) dz[1]=W[2]Tdz[2]×g[1]′(z[1])
d w [ 1 ] = 1 m d z [ 1 ] X T dw^{[1]}=\frac{1}{m}dz^{[1]}X^T dw[1]=m1dz[1]XT
d b [ 1 ] = 1 m db^{[1]}=\frac{1}{m} db[1]=m1np.sum( d z [ 1 ] dz^{[1]} dz[1],axis=1,keepdims=True)
随机初始化
- w [ 1 ] = w^{[1]}= w[1]=
np.random.randn((2,2))∗ 0.01 *0.01 ∗0.01
(w不可以为0,0.01是权重,权重小一点更可以适应于之前提到的激活函数) - b [ 1 ] = b^{[1]}= b[1]=
np.zero((2,1))
(b可以为0) - w [ 2 ] = w^{[2]}= w[2]=
np.random.randn((1,2))∗ 0.01 *0.01 ∗0.01 - b [ 2 ] = 0 b^{[2]}=0 b[2]=0
7、深层神经网络
数层数时:层数=隐层数+输出层
z [ l ] = w [ l ] a [ l − 1 ] + b [ l ] z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]} z[l]=w[l]a[l−1]+b[l]
a [ l ] = g [ l ] ( z [ l ] ) a^{[l]}=g^{[l]}(z^{[l]}) a[l]=g[l](z[l])
7.1 核对矩阵的维数
d w [ l ] , w [ l ] ∈ R n [ l ] × n [ l − 1 ] dw^{[l]},w^{[l]}\in \mathbb{R}^{n^{[l]}\times n^{[l-1]}} dw[l],w[l]∈Rn[l]×n[l−1]
d b [ l ] , b [ l ] ∈ R n [ l ] × 1 db^{[l]},b^{[l]}\in \mathbb{R}^{n^{[l]}\times 1} db[l],b[l]∈Rn[l]×1
Z [ l ] , A [ l ] ∈ R n [ l ] × m Z^{[l]},A^{[l]}\in \mathbb{R}^{n^{[l]}\times m} Z[l],A[l]∈Rn[l]×m
d z [ l ] , d a [ l ] ∈ R n [ l ] × m dz^{[l]},da^{[l]}\in \mathbb{R}^{n^{[l]}\times m} dz[l],da[l]∈Rn[l]×m
注意: A [ 0 ] = X A^{[0]}=X A[0]=X
7.2 前向和反向传播
前向:
Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} Z[l]=W[l]A[l−1]+b[l]
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]}=g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
反向:
d z [ l ] = d a [ l ] × g [ l ] ′ ( Z [ l ] ) dz^{[l]}=da^{[l]}\times g^{[l]'}(Z^{[l]}) dz[l]=da[l]×g[l]′(Z[l])
d w [ l ] = 1 m d z [ l ] × A [ l − 1 ] T dw^{[l]}=\frac{1}{m}dz^{[l]}\times A^{[l-1]T} dw[l]=m1dz[l]×A[l−1]T
d b [ l ] = 1 m db^{[l]}=\frac{1}{m} db[l]=m1np.sum( d z [ l ] dz^{[l]} dz[l],axis=1,keepdims=True)
d a [ l − 1 ] = w [ l ] T × d z [ l ] da^{[l-1]}=w^{[l]T}\times dz^{[l]} da[l−1]=w[l]T×dz[l]