本次实验使用paddle+LeNet5卷积神经网络实现,实现识别手写数字功能。
首先,先说明本次神经网络的细节。Lenet-5神经网络基本结构如下图所示:
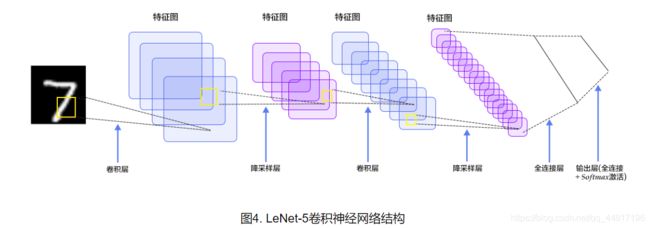
这里,我设定:
| 卷积层1 |
|
| 输入图片大小 |
28×28×1 |
| 卷积核大小 |
5×5 |
| 卷积核数量 |
20 |
| 步长 |
1 |
| 激活函数 |
relu |
| 输出大小 |
24×24×20 |
| 池化层1 |
|
| 输入 |
24×24×20 |
| 池大小 |
2×2 |
| 步长 |
2 |
| 输出大小 |
12×12×20 |
| 卷积层2 |
|
| 输入大小 |
12×12×20 |
| 卷积核大小 |
5×5 |
| 卷积核数量 |
20 |
| 步长 |
1 |
| 激活函数 |
relu |
| 输出大小 |
8×8×20 |
| 池化层2 |
|
| 输入 |
8×8×20 |
| 池大小 |
2×2 |
| 步长 |
2 |
| 输出大小 |
4×4×20 |
| 全连接层 |
|
| 输入 |
4×4×20 |
| 大小 |
10 |
| 激活函数 |
softmax |
到此,就确定好网络结构了。
下面是代码:
import paddle as paddle
import paddle.fluid as fluid
import matplotlib.pyplot as plt
import numpy as np
batch_size = 128 #设置每次获取的条数
buf_size = batch_size*100 #设置缓存条数
#获取数据载入内存的地址
train_reader = paddle.batch(paddle.reader.shuffle(paddle.dataset.mnist.train(), buf_size=buf_size), batch_size=batch_size)#训练数据地址
test_reader = paddle.batch(paddle.reader.shuffle(paddle.dataset.mnist.test(), buf_size=buf_size), batch_size=batch_size)#测试数据地址
#获取数据载入内存的地址
#建立神经网络结构
def convolutional_neural_network(img):#传入图片
#卷积层1+池化层1
conv_pool_1 = fluid.nets.simple_img_conv_pool(input=img, filter_size=5, num_filters=20, pool_size=2, pool_stride=2, act="relu")
#卷积层2+池化层2
conv_pool_2 = fluid.nets.simple_img_conv_pool(input=conv_pool_1, filter_size=5, num_filters=20, pool_size=2, pool_stride=2, act="relu")
#全连接层
prediction = fluid.layers.fc(input=conv_pool_2, size=10, act="softmax")
return prediction#返回结果
#建立神经网络结构
#创建img、label张量
#name的‘img’表示张量img,输入的照片大小shape要为28*28,而且是灰度图,因此为[1, 28, 28]
img = fluid.layers.data(name='img', shape=[1, 28, 28], dtype='float32')
label = fluid.layers.data(name='label', shape=[1], dtype='int64')#name的‘y’表示张量y,shape为1是因为得到的结果应该是0~9之间的一个数字
#创建img、label张量
#得到神经网络结构
predict = convolutional_neural_network(img)
#得到神经网络结构
#定义损失函数,此处用的是交叉熵
cost = fluid.layers.cross_entropy(input=predict, label=label)#建立交叉熵,标签是label
avg_cost = fluid.layers.mean(cost)#定义平均值
#定义损失函数
accuracy = fluid.layers.accuracy(input=predict, label=label)#定义精确度
#建立优化方法,这里用的是随机梯度下降法
optimizer = fluid.optimizer.Adam(learning_rate=0.001)#learning_rate表示学习速率,太低或太高都不能很好训练出好的分类器
optimizer.minimize(avg_cost)#优化准则是让交叉熵的均值(avg_cost)达到最小(minimize)
#建立优化方法
#分配内存、创建执行器、初始化
place = fluid.CPUPlace()#分配内存
exe = fluid.Executor(place)#定义执行器
exe.run(fluid.default_startup_program())#初始化,fluid.default_startup_program()表示默认初始化函数
#分配内存、创建执行器、初始化
#创建数值数据转换成img、label的特殊类型的数据类型转换器
feeder = fluid.DataFeeder(place=place, feed_list=[img, label])#投喂格式为[img, label],意味着第列表或者数组的第一个元素赋值给img,第二个元素赋值给label
#创建数值数据转换成img、label的特殊类型的数据类型转换器
#训练
print("training begin!")
train_costs = []#保存训练中的所有样本的交叉熵,用于作图,方便观察多次训练中交叉熵的变化趋势
train_accuracys = []#保存训练中的所有样本的精确度,用于作图,方便观察多次训练中精确度的变化趋势
times = []#保存训练累积的的数据量,以便后期作为每一次训练的MSE指标的横坐标轴的数据
time = 0#表示已经累积的训练的数据量
for i in range(5):#训练循环:5次
for index, data in enumerate(train_reader()):#根据train_reader保存的地址拿出数据下标以及数据,每次拿出batch_size条数据
#通过执行器执行fluid.default_main_program(),这是默认的训练函数,feed=feeder.feed(data)表示赋值给[img,label]的数据,fetch_list=[avg_cost, accuracy]表示优化参数是交叉熵的均值以及精确度
train_cost, train_accuracy = exe.run(program=fluid.default_main_program(), feed=feeder.feed(data), fetch_list=[avg_cost, accuracy])
train_costs.append(train_cost[0])#train_costs每次保存每个样本的交叉熵
train_accuracys.append(train_accuracy[0])#train_accuracys每次保存每个样本的精确度
time=time+batch_size
times.append(time)
# test_costs = []
# test_accuracys = []
for index, data in enumerate(test_reader()):#根据test_reader保存的地址拿出数据下标以及数据,每次拿出batch_size条数据
#通过执行器执行fluid.default_main_program(),这是默认的训练函数,feed=feeder.feed(data)表示赋值给[img,label]的数据,fetch_list=[avg_cost, accuracy]表示优化参数是交叉熵的均值以及精确度
test_cost,test_accuracy =exe.run(program=fluid.default_main_program(), feed=feeder.feed(data), fetch_list=[avg_cost, accuracy])
# test_costs.append(test_cost[0])
# test_accuracys.append(test_accuracy[0])
print("training over!")
#训练
#保存训练好的分类器、数据、执行器
inference_path = "d:/first_CNN"
fluid.io.save_inference_model(inference_path, ['img'], [predict], exe)
#保存训练好的分类器、数据、执行器
#画出交叉熵、精确度随着训练数据量增加而变化的图像
plt.plot(times, train_costs, "r-", label="train_cost")
plt.plot(times, train_accuracys, "g--", label="train_accuracy")
plt.xlabel("numOfData")
plt.ylabel("cost&accuracy")
plt.legend(loc="best")
plt.savefig("d:/result")
plt.show()
#画出交叉熵、精确度随着训练数据量增加而变化的图像
# print("test_avg_cost is:",sum(test_costs)/len(test_costs),"/ntest_avg_acc is:",sum(test_accuracys)/len(test_accuracys))
#创建预测执行器
infer_exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()
#创建预测执行器
infer_results = []#保存根据信息预测出来的数据(预测手写的数字的值)
trues = []#保存实际数据(这里指的是实际手写数字的值)
with fluid.scope_guard(inference_scope):
#根据保存的分类器路径以及预测执行器,创建出用来预测的分类模型,得到分类器、字段名以及模型的所有输出变量
[inference_program, feed_target_names, fetch_targets] = fluid.io.load_inference_model(inference_path, infer_exe)
#创建infer_reader张量,指向实际房价的内存空间,且导入150条
infer_reader = paddle.batch(paddle.dataset.mnist.test(), batch_size=150)
#导入数据
test_data = next(infer_reader())#迭代器,用于把数据导入变量
test_x = np.array([data[0].reshape(1,28,28) for data in test_data]).astype("float32")
test_y = np.array([data[1] for data in test_data]).astype("int64")
#导入数据
#预测
result = infer_exe.run(inference_program, feed={feed_target_names[0]:np.array(test_x)}, fetch_list=fetch_targets)
#预测
acc=0#定义保存预测对的数量的变量
print("inference result:")
for i, val in enumerate(result[0]):
index = np.argmax(val)#找出最大概率的下标
print(i,":",index)
infer_results.append(index)
print("true :")
for i, val in enumerate(test_y):
print(i,":",val)
trues.append(val)
for i in range(len(infer_results)):#比对预测值和实际值,得到共预测对的次数acc
if infer_results[i]==trues[i]:
acc=acc+1
# print("MSE is:",mean_squared_error(infer_results,trues))#对比实际值与预测值,算出均方差(MSE)
# print("infer_acc is:",accuracy_score(infer_results,trues))
print("acc is%0.3f"%(acc/len(infer_results)))#打印出精确度
由于训练循环为5次,因此每次运行时间大概需要数分钟时间。
但运行结束,即能得到交叉熵、精确率随训练样本量增加而变化的图像以及测试的精确率:
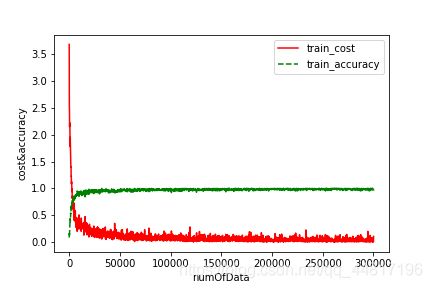
交叉熵、精确率随训练样本量增加而变化图

测试精确率图
| 精确率 |
大小 |
| 5次运行结果 |
0.993、1.000、0.993、0.993、0.993 |
由于偶然性,得到的精确率基本在0.99到1之间


