paddle手写数字识别解析(多方法)
paddle手写数字识别解析多方法
-
- 项目一
- 项目二
- 项目三
- 项目四
-
- 作者简介
项目传送门
如有不对请及时指出,非常感谢!
项目一
基于PaddlePaddle2.0-构建线性回归模型
理论可以看原文,非常详细,而且很细节(太菜了看不懂)
下面对代码解析和白话理解!
import numpy # 导入第三方库
num_inputs=2
num_examples=500
true_w=[1.2,2.5]
true_b=6.8
features = numpy.random.normal(0,1,(num_examples, num_inputs)).astype('float32') # 从正态(高斯)分布中抽取随机样本。
labels = features[:,0]*true_w[0]+features[:,1]*true_w[1]+true_b # 对正态数据进行加权处理
labels = labels + numpy.random.normal(0,0.001,labels.shape[0]) # 添加ε
labels = labels.astype('float32') # 转换数据为float32
labels = numpy.expand_dims(labels,axis=-1) #注意:需要在最后增加一个维度
print(labels.shape)
(500, 1)
print('features大小:', features.shape)
print('features[:,0]小:', features[:,0].shape)
features大小: (500, 2)
features[:,0]小: (500,)
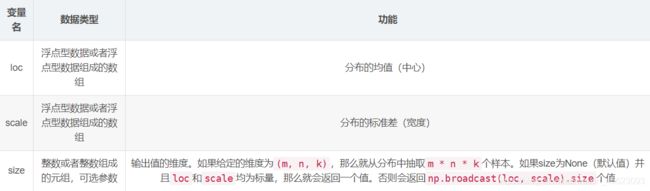
numpy.random.normal函数
numpy.random.normal(loc=0.0, scale=1.0, size=None)
从正态(高斯)分布中抽取随机样本。
import paddle # 导入第三方库
train_data=paddle.to_tensor(features) # 训练集转换为paddle Tensor
y_true=paddle.to_tensor(labels) # 测试集转换为paddle Tensor
model=paddle.nn.Linear(in_features=2, out_features=1) # 定义线性网络
paddle.nn.Linear(in_features, out_features, weight_attr=None, bias_attr=None, name=None):线性变换层-输出 官方文档传送门
# 查看网络
paddle.summary(model, (2,))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Linear-1 [[2]] [1] 3
===========================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
---------------------------------------------------------------------------
{'total_params': 3, 'trainable_params': 3}
# 随机梯度下降算法的优化器
sgd_optimizer=paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())
# loss计算
mse_loss=paddle.nn.MSELoss()
for i in range(5000): # 设置500个epoch
y_predict = model(train_data) # 训练集喂进模型
loss=mse_loss(y_predict, y_true) # 计算loss
loss.backward() # 反向传播
# 优化器进行优化
sgd_optimizer.step()
sgd_optimizer.clear_grad()
print(model.weight.numpy()) # 输出w的值
print(model.bias.numpy()) # 输出b的值
print(loss.numpy()) # 输出loss
[[1.1999037]
[2.4999018]]
[6.799708]
[1.0670032e-06]
设定w1 = 1.2 ,w2 = 2.5 ,b = 6.8
实际w1 = 1.99, w2 = 2.499,b = 6.799
效果比较好,拟合程度高
项目二
基于PaddlePaddle2.0-构建softmax分类器
理论可以看原文,非常详细,而且很细节(太菜了看不懂)
下面对代码解析和白话理解!
paddle.vision.datasets.MNIST MNIST 数据集 官方api传送门
import paddle
train_dataset=paddle.vision.datasets.MNIST(mode="train", backend="cv2") # 训练数据集
test_dataset=paddle.vision.datasets.MNIST(mode="test", backend="cv2") # 测试数据集
标签:就是这个图片的内容的一个结果,多半是数字属于自己定义的
print(train_dataset[0][0].shape) # 显示第一张图的大小
print(train_dataset[0][1]) # 查看第一张图的标签
print(train_dataset[0][0]) # 查看第一张图
(28, 28)
[5]
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 3. 18.
18. 18. 126. 136. 175. 26. 166. 255. 247. 127. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 30. 36. 94. 154. 170. 253.
253. 253. 253. 253. 225. 172. 253. 242. 195. 64. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 49. 238. 253. 253. 253. 253. 253.
253. 253. 253. 251. 93. 82. 82. 56. 39. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 18. 219. 253. 253. 253. 253. 253.
198. 182. 247. 241. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 80. 156. 107. 253. 253. 205.
11. 0. 43. 154. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 14. 1. 154. 253. 90.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 139. 253. 190.
2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 11. 190. 253.
70. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 35. 241.
225. 160. 108. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 81.
240. 253. 253. 119. 25. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
45. 186. 253. 253. 150. 27. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 16. 93. 252. 253. 187. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 249. 253. 249. 64. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
46. 130. 183. 253. 253. 207. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 39. 148.
229. 253. 253. 253. 250. 182. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 24. 114. 221. 253.
253. 253. 253. 201. 78. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 23. 66. 213. 253. 253. 253.
253. 198. 81. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 18. 171. 219. 253. 253. 253. 253. 195.
80. 9. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 55. 172. 226. 253. 253. 253. 253. 244. 133. 11.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 136. 253. 253. 253. 212. 135. 132. 16. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
import matplotlib.pyplot as plt
train_data0,train_label0=train_dataset[1][0],train_dataset[1][1] # 导出第二张图
train_data0=train_data0.reshape([28,28]) # 对第二张图进行转换
plt.figure(figsize=(5,5))
plt.imshow(train_data0,cmap=plt.cm.binary) # 显示图片
paddle.nn.Sequential(*layers):顺序容器。子Layer将按构造函数参数的顺序添加到此容器中。传递给构造函数的参数可以Layers或可迭代的name Layer元组。
paddle.nn.Flatten(start_axis=1, stop_axis=- 1):它实现将一个连续维度的Tensor展平成一维Tensor
里面第一层输入的数据是1,28,28的矩阵 经过数据压缩以后得到的是1,748的矩阵(1是标签,748是一维的图像)
导入线性层输入是748的数据输出是10
linear=paddle.nn.Sequential(
paddle.nn.Flatten(),#将[1,28,28]形状的图片数据改变形状为[1,784]
paddle.nn.Linear(784,10)
)
#利用paddlepaddle2的高阶功能,可以大幅减少训练和测试的代码量
model=paddle.Model(linear)
# 查看网络
model.summary((1, 28, 28))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Flatten-2 [[1, 28, 28]] [1, 784] 0
Linear-3 [[1, 784]] [1, 10] 7,850
===========================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.03
Estimated Total Size (MB): 0.04
---------------------------------------------------------------------------
{'total_params': 7850, 'trainable_params': 7850}
paddle.Modle.prepare(optimizer=None, loss_function=None, metrics=None):用于配置模型所需的部件,比如优化器、损失函数和评价指标。
paddle.optimizer.Adam:Adam优化器,能够利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
paddle.nn.CrossEntropyLoss:该OP计算输入input和标签label间的交叉熵损失 ,它结合了 LogSoftmax 和 NLLLoss 的OP计算,可用于训练一个 n 类分类器。分类器
paddle.metric.Accuracy:计算准确率(accuracy)
paddle.Modle.fit:训练模型
evaluate(eval_data, batch_size=1, log_freq=10, verbose=2, num_workers=0, callbacks=None):在输入数据上,评估模型的损失函数值和评估指标.
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(), # 交叉熵损失函数。线性模型+该损失函数,即softmax分类器。
paddle.metric.Accuracy(topk=(1,2)))
model.fit(train_dataset, # 训练数据集
epochs=2, # 训练的总轮次
batch_size=64, # 训练使用的批大小
verbose=1) # 日志展示形式
model.evaluate(test_dataset,batch_size=64,verbose=1) # 评估
The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/2
step 938/938 [==============================] - loss: 6.2703 - acc_top1: 0.8861 - acc_top2: 0.9578 - 3ms/step loss: 2.4789 - acc_top1: 0.8855 - acc
Epoch 2/2
step 938/938 [==============================] - loss: 2.5008 - acc_top1: 0.8862 - acc_top2: 0.9589 - 3ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.2525 - acc_top1: 0.8896 - acc_top2: 0.9564 - 2ms/step
Eval samples: 10000
{'loss': [0.25250664], 'acc_top1': 0.8896, 'acc_top2': 0.9564}
模型在测试集上的top1准确率达到: 0.8896, top2准确率达到: 0.9564
项目三
基于PaddlePaddle2.0-构建多层感知机模型
理论可以看原文,非常详细,而且很细节(太菜了看不懂)
下面对代码解析和白话理解!
# 导入第三方库
import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import ToTensor
#导入数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", transform=ToTensor())
val_dataset=paddle.vision.datasets.MNIST(mode="test", transform=ToTensor())
#定义模型
class MLPModel(paddle.nn.Layer): # 继承paddle.nn.Layer类
def __init__(self):
super(MLPModel, self).__init__()
self.flatten=paddle.nn.Flatten() # 数据拉直
self.hidden=paddle.nn.Linear(in_features=784,out_features=128) # 线性输入784输出128
self.output=paddle.nn.Linear(in_features=128,out_features=10) # 线性输入128输出10
def forward(self, x):
x=self.flatten(x) # 拉直
x=self.hidden(x) # 经过隐藏层(线性层1)
x=F.relu(x) # 经过激活层
x=self.output(x) # 经过输出层
return x
model=paddle.Model(MLPModel()) # 实例化模型
# 查看网络
model.summary((1, 28, 28))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Flatten-9 [[1, 28, 28]] [1, 784] 0
Linear-2 [[1, 784]] [1, 128] 100,480
Linear-3 [[1, 128]] [1, 10] 1,290
===========================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.39
Estimated Total Size (MB): 0.40
---------------------------------------------------------------------------
{'total_params': 101770, 'trainable_params': 101770}
model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(),
paddle.metric.Accuracy())
model.fit(train_dataset,
val_dataset,
epochs=5,
batch_size=64,
verbose=1)
The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/5
step 938/938 [==============================] - loss: 0.1415 - acc: 0.9516 - 20ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.1010 - acc: 0.9603 - 18ms/step
Eval samples: 10000
Epoch 2/5
step 938/938 [==============================] - loss: 0.0513 - acc: 0.9695 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0100 - acc: 0.9707 - 19ms/step
Eval samples: 10000
Epoch 3/5
step 938/938 [==============================] - loss: 0.0277 - acc: 0.9783 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0137 - acc: 0.9739 - 19ms/step
Eval samples: 10000
Epoch 4/5
step 938/938 [==============================] - loss: 0.0104 - acc: 0.9828 - 20ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0061 - acc: 0.9766 - 19ms/step
Eval samples: 10000
Epoch 5/5
step 938/938 [==============================] - loss: 0.0913 - acc: 0.9863 - 20ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 5.5464e-04 - acc: 0.9776 - 19ms/step
Eval samples: 10000
# 模型评估,根据prepare接口配置的loss和metric进行返回
result = model.evaluate(val_dataset,verbose=1)
print(result)
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 10000/10000 [==============================] - loss: 3.0994e-06 - acc: 0.9776 - 2ms/step
Eval samples: 10000
{'loss': [3.0994463e-06], 'acc': 0.9776}
测试集上的分类准确率达到:0.9776
项目四
基于PaddlePaddle2.0-构建卷积网络-LeNet5
理论可以看原文,非常详细,而且很细节(太菜了看不懂)
下面对代码解析和白话理解!
import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import Compose, Normalize
# 数据处理(归一化)(把0-255的归一到-1~1)
transform = Compose([Normalize(mean=[127.5],
std=[127.5],
data_format='CHW')])
#导入MNIST数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", transform=transform)
val_dataset=paddle.vision.datasets.MNIST(mode="test", transform=transform)
#定义模型
class LeNetModel(paddle.nn.Layer):
def __init__(self):
super(LeNetModel, self).__init__()
# 创建卷积和池化层块,每个卷积层后面接着2x2的池化层
#卷积层L1
self.conv1 = paddle.nn.Conv2D(in_channels=1,
out_channels=6,
kernel_size=5,
stride=1)
#池化层L2
self.pool1 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2)
#卷积层L3
self.conv2 = paddle.nn.Conv2D(in_channels=6,
out_channels=16,
kernel_size=5,
stride=1)
#池化层L4
self.pool2 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2)
#线性层L5
self.fc1=paddle.nn.Linear(256,120)
#线性层L6
self.fc2=paddle.nn.Linear(120,84)
#线性层L7
self.fc3=paddle.nn.Linear(84,10)
#正向传播过程
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.pool1(x)
x = F.relu(x)
x = self.conv2(x)
x = self.pool2(x)
x = paddle.flatten(x, start_axis=1,stop_axis=-1)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
out = self.fc3(x)
return out
model=paddle.Model(LeNetModel())
print(train_dataset[0][0].shape)
(1, 28, 28)
# 查看网络
model.summary((1, 1, 28, 28))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Conv2D-3 [[1, 1, 28, 28]] [1, 6, 24, 24] 156
MaxPool2D-3 [[1, 6, 24, 24]] [1, 6, 12, 12] 0
Conv2D-4 [[1, 6, 12, 12]] [1, 16, 8, 8] 2,416
MaxPool2D-4 [[1, 16, 8, 8]] [1, 16, 4, 4] 0
Linear-7 [[1, 256]] [1, 120] 30,840
Linear-8 [[1, 120]] [1, 84] 10,164
Linear-9 [[1, 84]] [1, 10] 850
===========================================================================
Total params: 44,426
Trainable params: 44,426
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.04
Params size (MB): 0.17
Estimated Total Size (MB): 0.22
---------------------------------------------------------------------------
{'total_params': 44426, 'trainable_params': 44426}
model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(),
paddle.metric.Accuracy())
model.fit(train_dataset,
val_dataset,
epochs=5,
batch_size=64,
verbose=1)
The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/5
step 938/938 [==============================] - loss: 0.0166 - acc: 0.9680 - 18ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0015 - acc: 0.9735 - 9ms/step
Eval samples: 10000
Epoch 2/5
step 938/938 [==============================] - loss: 0.0098 - acc: 0.9829 - 18ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0014 - acc: 0.9844 - 9ms/step
Eval samples: 10000
Epoch 3/5
step 938/938 [==============================] - loss: 0.0223 - acc: 0.9878 - 19ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0382 - acc: 0.9851 - 9ms/step
Eval samples: 10000
Epoch 4/5
step 938/938 [==============================] - loss: 0.0056 - acc: 0.9905 - 18ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 1.7806e-04 - acc: 0.9850 - 9ms/step
Eval samples: 10000
Epoch 5/5
step 938/938 [==============================] - loss: 0.0133 - acc: 0.9928 - 18ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 4.5182e-04 - acc: 0.9848 - 9ms/step
Eval samples: 10000
# 模型评估,根据prepare接口配置的loss和metric进行返回
result = model.evaluate(val_dataset,verbose=1)
print(result)
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 10000/10000 [==============================] - loss: 5.9605e-07 - acc: 0.9848 - 3ms/step
Eval samples: 10000
{'loss': [5.960466e-07], 'acc': 0.9848}
测试集上的分类准确率达到:0.9848
作者简介
作者:三岁
经历:自学python,现在混迹于paddle社区,希望和大家一起从基础走起,一起学习Paddle
csdn地址:https://blog.csdn.net/weixin_45623093/article/list/3
我在AI Studio上获得黄金等级,点亮7个徽章,来互关呀~ https://aistudio.baidu.com/aistudio/personalcenter/thirdview/284366
传说中的飞桨社区最差代码人,让我们一起努力!
记住:三岁出品必是精品 (不要脸系列)
