头歌平台 --- 机器学习 --- 高斯混合聚类
第1关:高斯混合聚类的核心思想
- 任务描述
- 相关知识
- 高斯混合分布
- 高斯混合聚类的核心思想
- 编程要求
- 测试说明
任务描述
本关任务:根据本节课所学知识完成本关所设置的选择题。
相关知识
为了完成本关任务,你需要掌握:
- 高斯混合分布;
- 高斯混合聚类的核心思想。
高斯混合分布
高斯混合聚类认为数据集中样本的产生过程是由高斯混合分布所给出的。那什么是高斯混合分布呢?
其实很简单,以下面三个图为例:白色的样本点由高斯分布 A 产生、蓝色的样本点由高斯分布 B 产生、灰色的样本点由高斯分布 C 产生。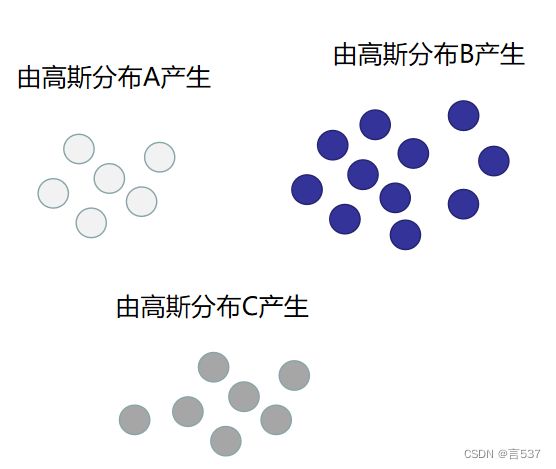
如果仅仅想用一个分布来描述这 3 个高斯分布的话,我们下意识地可能会觉得如果我的分布如下图中红色部分所示,就相当于用一个分布描述了 3 个高斯分布。
上图中红色的分布其实就是高斯混合分布。高斯混合分布其实就是多个高斯分布的带权线性加和。例如上图中红色的分布等于0.2*高斯分布A+0.5*高斯分布B+0.3*高斯分布C。
现在我们对高斯混合分布有了一定的感官上的认识,下面我们给出高斯混合分布的数学定义。设pM(x)为样本x所服从的概率密度函数(高斯混合分布的概率密度函数),则有:
pM(x)=i=1∑kαi∗p(x∣μi,Σi)
并有:
∑kαi=1,αi>0
其中αi表示第i个高斯分布的系数,p(x∣μi,Σi)为均值向量为μi,协方差矩阵为Σi的高斯分布。
所以在使用高斯混合聚类时,对于样本的产生过程有这样的假设:
-
首先,根据α1,α2,...,αk定义的先验分布选择高斯分布,其中αi为选择第i个高斯分布的概率(这也是所有α的和为1的原因)。
-
然后,根据被选择的混合成分的概率密度函数进行采样,从而生成相应的样本。
高斯混合聚类的核心思想
现在对样本集D={x1,x2,...,xm}使用高斯混合聚类划分成k个簇。高斯混合聚类会怎样想呢?其实很简单,如果能分别计算出x1属于1号簇的概率,x1属于2号簇的概率,...,xk属于k号簇的概率。接着将概率最大的簇作为聚类结果就好了。同样,样本集中的其他样本也如法炮制,就能实现对样本集的聚类。
那么接下来的问题就是怎样计算这个概率?
想要计算这个概率,可以令随机变量zj∈{1,2,...,k}表示样本xi是从1到k这k个高斯分布中的哪个高斯分布通过采样所得到的(假如z1=2表示x1这个样本属于第2个高斯分布,也就是说x1这个样本属于2号簇)。
有了zj这个随机变量后,就可以使用贝叶斯公式将pM(zj=i∣xj)(即xj属于第i个高斯分布的概率)计算出来了。
pM(zj=i∣xj)=pM(xj)P(zj=i)∗pM(xj∣zj=i)=∑l=1kαl∗p(xj∣μl,Σl)αi∗p(xj∣μi,Σi)
为了方便描述,我们不妨将pM(zj=i∣xj)记成τji。所以当高斯混合分布已知时,高斯混合聚类将会把样本集D划分为k个簇,每个样本xj的簇标记λj以如下方式确定:
λj=argmaxi∈{1,2,..,k}τji
编程要求
根据本关所学习到的知识,完成所有选择题。
测试说明
略
开始你的任务吧,祝你成功!
第2关:实现高斯混合聚类
- 任务描述
- 相关知识
- 高斯混合聚类算法的流程
- 编程要求
- 测试说明
任务描述
本关任务:用 python 实现高斯混合聚类算法。请不要修改 Begin-End 段之外的代码。
相关知识
为了完成本关任务,你需要掌握高斯混合聚类算法的流程
高斯混合聚类算法的流程
在上一关中已经介绍了高斯混合聚类算法的核心思想,并知道τji与αi,μi,Σi有关。所以高斯混合聚类算法的训练过程就是找到合适的αi,μi,Σi的过程。在高斯混合聚类算法中通常使用 EM 算法来估计这些参数。
EM 算法的 E 步比较简单,就是根据当前的αi,μi,Σi计算出τji。麻烦的是 M 步, M 步中需要知道怎样更新αi,μi,Σi。所以我们不妨简单地推导一下。
假设有一个包含m条样本的数据集D,那么似然函数L(D)如下:
L(D)=j=1∏mpM(xj)
则其对数似然函数LL(D)如下:
LL(D)=i=1∑mln(i=1∑kαi∗p(xj∣μi,Σi))
为了使得LL(D)最大化,则需要分别计算偏导,并使得偏导为$$0 $$。因此计算结果如下:
μi=∑j=1mτji∑j=1mτjixj
Σi=∑j=1mτji∑j=1mτji(xj−μi)(xj−ui)T
αi=m1i=1∑mτji
所以 EM 算法的 M 步就是根据上面的式子更新参数。
最后总结一下高斯混合聚类算法的流程。
- 初始化参数;
- EM 算法更新参数;
- 根据高斯混合分布确定簇的划分。
编程要求
根据提示,在右侧编辑器补充 Begin-End 段中的代码,完成 fit 函数和 predict 函数。fit 函数需要完成的功能是根据高斯混合聚类算法的训练流程将参数分别保存至 self.alpha, self.mu, self.sigma 中。predict 函数需要完成的功能是对数据集进行聚类,并将聚类结果返回。
提示:计算p(x∣μi,Σi)可以使用如下代码:
from scipy.stats import multivariate_normal'''计算data在均值向量为mu,协方差矩阵为sigma的高斯分布下的概率'''p = multivariate_normal(mean=mu, cov=sigma).pdf(data)
测试说明
平台会对你编写的代码进行测试,你只需完成 fit 函数和 predict 函数即可,聚类结果的 FM 指数高于 0.9 视为过关。
测试输入: 预期输出:你的 FM 指数高于 0.9!
开始你的任务吧,祝你成功!
import numpy as np
from scipy.stats import multivariate_normal
import numpy as np
def multiGaussian(x,mu,sigma):
return 1/((2*np.pi)*pow(np.linalg.det(sigma),0.5))*np.exp(-0.5*(x-mu).dot(np.linalg.pinv(sigma)).dot((x-mu).T))
def computeGamma(X,mu,sigma,alpha,multiGaussian):
n_samples=X.shape[0]
n_clusters=len(alpha)
gamma=np.zeros((n_samples,n_clusters))
p=np.zeros(n_clusters)
g=np.zeros(n_clusters)
for i in range(n_samples):
for j in range(n_clusters):
p[j]=multiGaussian(X[i],mu[j],sigma[j])
g[j]=alpha[j]*p[j]
for k in range(n_clusters):
gamma[i,k]=g[k]/np.sum(g)
return gamma
class GMM(object):
def __init__(self, n_components, max_iter=100):
'''
构造函数
:param n_components: 想要划分成几个簇,类型为int
:param max_iter: EM的最大迭代次数
'''
self.n_components = n_components
self.ITER = max_iter
def fit(self, train_data):
'''
训练,将模型参数分别保存至self.alpha,self.mu,self.sigma中
:param train_data: 训练数据集,类型为ndarray
:return: 无返回
'''
n_samples,n_features=train_data.shape
mu=train_data[np.random.choice(range(n_samples),self.n_components )]
alpha=np.ones(self.n_components )/self.n_components
sigma=np.full((self.n_components ,n_features,n_features),np.diag(np.full(n_features,0.1)))
for i in range(self.ITER):
gamma=computeGamma(train_data,mu,sigma,alpha,multiGaussian)
alpha=np.sum(gamma,axis=0)/n_samples
for i in range(self.n_components ):
mu[i]=np.sum(train_data*gamma[:,i].reshape((n_samples,1)),axis=0)/np.sum(gamma,axis=0)[i]
sigma[i]=0
for j in range(n_samples):
sigma[i]+=(train_data[j].reshape((1,n_features))-mu[i]).T.dot((train_data[j]-mu[i]).reshape((1,n_features)))*gamma[j,i]
sigma[i]=sigma[i]/np.sum(gamma,axis=0)[i]
self.mu=mu
self.sigma=sigma
self.alpha=alpha
def predict(self, test_data):
'''
预测,根据训练好的模型参数将test_data进行划分。
注意:划分的标签的取值范围为[0,self.n_components-1],即若self.n_components为3,则划分的标签的可能取值为0,1,2。
:param test_data: 测试集数据,类型为ndarray
:return: 划分结果,类型为你ndarray
'''
#********* Begin *********#
pred=computeGamma(test_data,self.mu,self.sigma,self.alpha,multiGaussian)
results=np.argmax(pred,axis=1)
return results
#********* End *********#
第3关:图像分割
- 任务描述
- 相关知识
- 聚类与图像分割
- 图像的基础操作
- 如何使用 GaussianMixture
- 编程要求
- 测试说明
任务描述
本关任务:编写一个程序对图像进行分割。
原图如下:
分割图像如下:
相关知识
为了完成本关任务,你需要掌握:
-
聚类与图像分割;
-
图像的基础操作;
-
如何使用 GaussianMixture。
聚类与图像分割
图像分割非常好理解,如上面的图所示,就是将图像划分成若干个不同的部分(分割结果可以看出将原图划分成了 3 个部分:道路、树林、天空)。
那么图像分割怎样和聚类扯上关系呢?很简单,我们知道一副彩色图像是由多个像素点组成的。若把每个像素点看成是一个样本的话,我们就可以通过聚类的方式给每个像素点打上簇标记(比如 0,1,2)。然后再根据簇标记将像素点设置成想要的颜色(比如簇标记为 0 的设置成黄色,簇标记为 1 的设置成绿色,簇标记为 2 的设置成蓝色),然后可视化出来就能得到图像分割的效果。
那么怎样将一副图像转换成我们通常想要的类似表格的数据呢?也很简单,一副彩色图像是由多个像素点组成的,而一个像素点一般是由 R,G,B 三个通道组成的。那么我们可以把每一个像素点看成是数据集中的一个样本,每个样本包含 3 个特征( RGB 三个通道的值)。所以如果一副彩色图的高是 200,宽是 300。则该图可以看成是一个 60000 行,3 列的数据集。有了我们喜闻乐见的表格数据后,就可以将数据传递给聚类算法进行聚类了。
如果你对数字图像处理中的阈值化感兴趣,可以 点这里 学习怎样用另一种思来实现图像分割。
图像的基础操作
我们可以使用 PIL 来对图像进行操作。如果你想读取一幅图或者保存一副图,代码如下:
from PIL import Image# 读取road.jpg到im变量中im = Image.open('road.jpg')# 将im保存为new_road.jpgim.save('new_road.jpg')
值得注意的是,当使用 open 函数读取到图像后,我们不能直接将图像传给 sklearn 的聚类算法接口。因为此时的 im 不是 ndarray 或者 list ,而且 im 的形状不是喜闻乐见的表格的形状。所以需要进行转换,代码如下:
import numpy as np# 将im转换成ndarrayimg = np.array(im)# 将img变形为[-1, 3]的shape,并保存至img_reshapeimg_reshape = img.reshape(-1, 3)
当聚类算法给出结果后,我们需要根据聚类结果给图像上色,代码如下:
# pred为聚类算法的预测结果,将簇为0的点设置成红色,簇为1的点设置成蓝色img[pred == 0, :] = [255, 0, 0]img[pred == 1, :] = [0, 0, 255]
由于 img 为 ndarray,我们需要将其转成 Image 类型才能使用 save 函数实现保存图片的功能。转换代码如下:
im = Image.fromarray(img.astype('uint8'))
如何使用 GaussianMixture
GaussianMixture 是 sklearn 提供的高斯混合聚类的一个类,该类的构造函数中可以根据实际需要设置很多参数。但常用的参数是 n_components 和 max_iter。其中:
- n_components :想要聚成几个簇,类型为 int;
- max_iter :迭代次数,类型为 int。
使用 GaussianMixture 进行聚类很简单,fit-predict 大法就完事了。代码如下:
# 实例化一个将数据聚成2个簇的高斯混合聚类器gmm = GaussianMixture(2)# 将数据传给fit函数,fit函数会计算出各个高斯分布的参数和响应系数gmm.fit(img_reshape)# 对数据进行聚类,簇标记为0或1(因为gmm对象想要聚成2个簇)pred = gmm.predict(img_reshape)# 图省事可以这样,相当于调用了fit之后调用predictpred = gmm.fit_predict(img_reshape)
编程要求
在右侧编辑器的 begin-end 之间补充代码,你所需要完成的功能是:
-
读取
./step3/image/test.jpg; -
将读取到的图像分割成 3 个部分。其中簇标记为 0 的部分用黄色表示;簇标记为 1 的部分用蓝色表示;簇标记为 2 的部分用绿色表示;
-
将分割后的图像保存至
./step3/dump/result.jpg
测试说明
只需将分割后的图像保存到正确的位置即可,平台内部会计算你的结果与正确答案的差异程度,差异程度小于 10 视为过关。
预期输出:你的分割结果与正确答案的差异度小于 10!
开始你的任务吧,祝你成功!
from PIL import Image
import numpy as np
from sklearn.mixture import GaussianMixture
#******** Begin *********#
im = Image.open('./step3/image/test.jpg')
img = np.array(im)
img_reshape = img.reshape(-1,3)
gmm = GaussianMixture(n_components=3,covariance_type='full')
pred = gmm.fit_predict(img_reshape)
img_reshape[pred == 0, :] = [255,255,0]
img_reshape[pred==1,:] = [0,0,255]
img_reshape[pred==2,:] = [0,255,0]
im = Image.fromarray(img.astype('uint8'))
im.save('./step3/dump/result.jpg')
#********* End *********#



