【机器学习】聚类【Ⅲ】高斯混合模型讲解

主要来自周志华《机器学习》一书，数学推导主要来自简书博主“形式运算”的原创博客，包含自己的理解。
有任何的书写错误、排版错误、概念错误等，希望大家包含指正。

由于字数限制，分成五篇博客。
【机器学习】聚类【Ⅰ】基础知识与距离度量
【机器学习】聚类【Ⅱ】原型聚类经典算法
【机器学习】聚类【Ⅲ】高斯混合模型讲解
【机器学习】聚类【Ⅳ】高斯混合模型数学推导
【机器学习】聚类【Ⅴ】密度聚类与层次聚类

4.6 高斯混合聚类

4.6.1 一元高斯分布

高斯分布（Gaussian distribution），也称正态分布（Normal distribution），又名“常态分布”。若一维随机变量 $x$ 服从一个位置参数为 $\mu$、尺度参数为$\sigma$ 的正态分布，则其概率密度函数为
$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\text{\hspace{1em}(34)}$$
特别地，当 $\mu =0$，$\sigma =1$ 时，正态分布为标准正态分布
$$p(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}\text{\hspace{1em}(35)}$$

4.6.2 多元高斯分布

多元高斯分布亦称为多元正态分布，是单维正态分布向多维的推广。假设 $n$ 维随机变量 $xx=(x_1;x_2;\cdot \cdot \cdot ;x_n)$ 的每一维互不相关且服从正态分布，则其概率密度函数为
$$p(xx)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma \Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(xx-\mu \mu {)}^T{\Sigma \Sigma }^{-1}(xx-\mu \mu )}\text{\hspace{1em}(36)}$$
其中 $\mu \mu$ 是 $n$ 维均值向量，$\Sigma \Sigma$ 是 $n\times n$ 的协方差矩阵。由式 $(36)$ 可看出，高斯分布完全由均值向量 $\mu \mu$ 和协方差矩阵 $\Sigma \Sigma$ 这两个参数确定。为了明确显示高斯分布与相应参数的依赖关系，将概率密度函数记为 $p(xx\mid \mu \mu ,\Sigma \Sigma )$ 。

一元高斯分布到多元高斯分布的推导：

为了区分一元高斯分布和多元高斯分布的概率密度函数，分别用符号 $p()$ 和 $f()$ 表示。

各个维度的均值 $\mu \mu =({\mu }_1;{\mu }_2;\cdot \cdot \cdot ;{\mu }_n)$，方差 $\sigma \sigma =({\sigma }_1;{\sigma }_2;\cdot \cdot \cdot ;{\sigma }_n)$ 。根据联合概率密度公式
$$f(xx)=f(x_1,x_2,\cdot \cdot \cdot ,x_n)=p(x_1)p(x_2)\cdot \cdot \cdot p(x_n)=\frac{1}{(\sqrt{2\pi }{)}^n{\sigma }_1{\sigma }_2\cdot \cdot \cdot {\sigma }_n}{e}^{-\frac{(x_1-{\mu }_1{)}^2}{2{\sigma }_1^2}-\frac{(x_2-{\mu }_2{)}^2}{2{\sigma }_2^2}\cdot \cdot \cdot -\frac{(x_n-{\mu }_n{)}^2}{2{\sigma }_n^2}}\text{\hspace{1em}(37)}$$
令 $z^2=\frac{(x_1-{\mu }_1{)}^2}{2{\sigma }_1^2}+\frac{(x_2-{\mu }_2{)}^2}{2{\sigma }_2^2}+\cdot \cdot \cdot +\frac{(x_n-{\mu }_n{)}^2}{2{\sigma }_n^2}$，${\sigma }_z={\sigma }_1{\sigma }_2\cdot \cdot \cdot {\sigma }_n$，如此将多元高斯分布转换为与一元高斯分布比较接近的形式
$$f(z)=\frac{1}{(\sqrt{2\pi }{)}^n{\sigma }_z}{e}^{-\frac{z^2}{2}}\text{\hspace{1em}(38)}$$
因为多元高斯分布有着很强的几何思想，单纯从代数的角度看待 $z$ 很难看出 $z$ 的概率分布规律，这里需要转换成矩阵形式
$$z^2=z^{T}z=(x_1-{\mu }_1,x_2-{\mu }_2,\cdot \cdot \cdot ,x_n-{\mu }_n)\left(\begin{array}{cccc}\frac{1}{{\sigma }_1^2}& 0& \cdots & 0\\ 0& \frac{1}{{\sigma }_2^2}& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & \frac{1}{{\sigma }_n^2}\end{array}\right)(x_1-{\mu }_1,x_2-{\mu }_2,\cdot \cdot \cdot ,x_n-{\mu }_n{)}^T\text{\hspace{1em}(39)}$$
定义符号
$$\Sigma \Sigma =\left(\begin{array}{cccc}{\sigma }_1^2& 0& \cdots & 0\\ 0& {\sigma }_2^2& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & {\sigma }_n^2\end{array}\right)$$
$\Sigma \Sigma$ 代表变量 $xx$ 的协方差矩阵，$i$ 行 $j$ 列的元素值表示 $x_i$ 与 $xj$ 的协方差。因为现在变量之间是相互独立的，所以只有对角线上（$i=j$）存在元素，其它位置都是 $0$，且 $x_i$ 与它本身的协方差就等于方差。

$\Sigma \Sigma$ 是一个对角阵，根据对角矩阵的性质，若 $\Sigma \Sigma$ 为非奇异阵，则其逆矩阵为

$${\Sigma \Sigma }^{-1}=\left(\begin{array}{cccc}\frac{1}{{\sigma }_1^2}& 0& \cdots & 0\\ 0& \frac{1}{{\sigma }_2^2}& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & \frac{1}{{\sigma }_n^2}\end{array}\right)$$
另外，${\sigma }_z$ 也可以通过 $\Sigma \Sigma$ 表示
$${\sigma }_z=|\Sigma \Sigma {|}^{\frac{1}{2}}={\sigma }_1{\sigma }_2\cdot \cdot \cdot {\sigma }_n\text{\hspace{1em}(40)}$$
式 $(39)$ 可简化为
$$z^{T}z=(xx-\mu \mu {)}^T{\Sigma \Sigma }^{-1}(xx-\mu \mu )\text{\hspace{1em}(41)}$$
将式 $(40)$ 和式 $(41)$ 代回式 $(38)$ 得
$$f(xx)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma \Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(xx-\mu \mu {)}^T{\Sigma \Sigma }^{-1}(xx-\mu \mu )}$$
即等价于式 $(36)$，推导完毕。

4.6.3 单高斯分布模型

单高斯分布模型（Gaussian Single Model，简称 GSM）就是正态分布。因此， GSM 只能用于计算样本属于该模型的概率，设定阈值进而判断样本是否属于该模型。

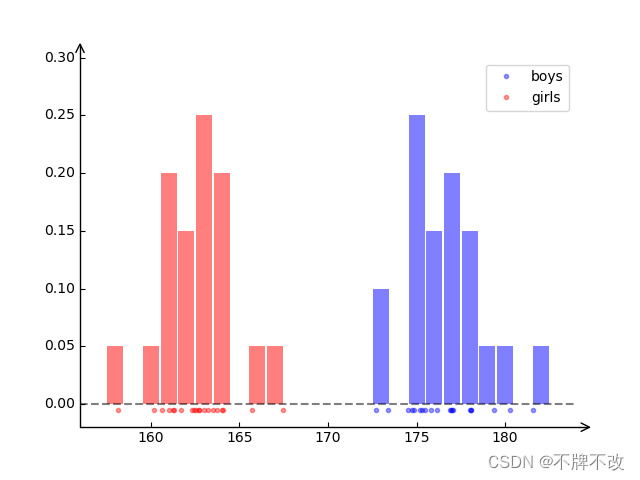
以一维样本为例，假设存在一组男生身高和女生身高如下

男生	176.17	176.89	172.73	180.28	173.41	175.32	178.01	174.51	174.88	175.18	178.10	181.58	177.08	174.76	178.08	175.81	176.96	179.35	175.50	177.02
女生	161.24	162.69	163.51	161.02	162.32	162.53	161.72	160.62	160.16	162.69	162.46	167.46	158.13	163.23	163.74	165.72	164.00	161.31	163.00	164.08

表 3    男女身高

绘制散点图与频次柱状图如图 $6$ 所示。

图 6    男女身高频次柱状图

显然，用一个高斯分布是无法准确表达男生女生身高分布，对于这组数据最起码应该用两个高斯分布来描述。可见，GSM 无法实现多分类，所以引入了混合高斯模型（Gaussian Mixture Model，简称 GMM，也译为 Mixture-of-Gaussian，简称MOG）。

4.6.4 高斯混合模型

可定义高斯混合分布
$$p_{\mathcal{M}}(xx)=\sum _{i=1}^k{\alpha }_i\cdot p(xx\mid {\mu \mu }_i,{\Sigma \Sigma }_i)\text{\hspace{1em}(42)}$$
该分布共由 $k$ 个混合成分组成，每个混合成分对应一个高斯分布。其中 ${\mu \mu }_i$ 与 ${\Sigma \Sigma }_i$ 是第 $i$ 个高斯混合成分的参数，而 ${\alpha }_i>0$ 为相应的“混合系数”（mixture coefficient)，${\sum }_{i=1}^k{\alpha }_i=1$ 。

直观上，高斯混合模型就是将多个高斯分布加权，使模型能够描述满足不同高斯分布的数据。假设男生身高满足 $({\mu }_{boys},{\sigma }_{boys})=(177,2)$，女生身高满足 $({\mu }_{girls},{\sigma }_{girls})=(163,2)$，男生和女生的高斯分布曲线图如图 $7$ 所示。

图 7    男女身高高斯分布曲线

图 $8$ 左图所示为直接将两个分布相加和两个分布带权相加，我们知道男女比例大致为 $1:1$，所以假设权重 ${\alpha }_{boys}={\alpha }_{girls}=\frac{1}{2}$ 。

图 8    高斯混合分布曲线

当满足 ${\sum }_{i=1}^k{\alpha }_i=1$ 时，$p_{\mathcal{M}}(\cdot )$ 也是概率密度函数，即 $\int p_{\mathcal{M}}(xx)dxx=1$ 。

我觉得设定权重且规定权重和为 $1$ 的原因有四点。

第一点是凑概率密度函数，保证积分值为 $1$，更贴近概率模型。

第二点是用权重表示先验概率，即 ${\alpha }_i$ 表示属于（任何）样本属于第 $i$ 个簇的概率，或者说满足第 $i$ 个混合成分分布的概率，如此便可以将高斯混合分布 $p_{\mathcal{M}}(xx,\mu \mu ,\Sigma \Sigma )$ （更详细准确的模型表达形式，其中 $\mu \mu =({\mu \mu }_1,{\mu \mu }_2,\cdot \cdot \cdot ,{\mu \mu }_k)$ ，$\Sigma \Sigma$ 同理）理解为全概率，即将对样本 $xx$ 在参数为 $(\mu \mu ,\Sigma \Sigma )$ 的模型中出现的概率求解问题转化为了在不同混合成分（参数为 $({\mu \mu }_i,{\Sigma \Sigma }_i)$ 的高斯分布）中样本 $xx$ 出现概率求和的简单问题。这样可以认为是对高斯混合分布函数，即式 $(42)$ 的另一种理解。

剩下两点暂时不讲，最后进行说明。

高斯混合分布中的每个混合成分都对应着一个簇，混合成分函数值表示样本属于该簇的概率，那么高斯混合分布函数值就表示样本属于各个簇概率的加权，即样本属于这些簇的概率，或者说样本满足这个模型的概率。

一般是认为高斯混合分布在混合成分足够多的时候可以模拟任何分布。注意这里的关键在于「混合」而不是「高斯」，也就是说，重要的是各个分量之间的位置关系，而不是每个分量的形状。每个混合成分取为高斯，只是因为它的性质比较良好（比如密度函数处处可导），计算也相对简单。另外，根据中心极限定理的推广，可以认为自然界的很多现象都是由无数微小因素的叠加而产生的，而无论这种因素服从何种分布，在大尺度上来观察，其结果都应大致符合正态分布。因此，采用正态分布可能更加合理。

4.6.5 高斯混合模型的 EM 算法

我们知道 EM 算法用于含有隐变量概率模型参数的极大似然估计。存在隐变量可以理解为存在相互依赖关系，比如 $k$-means 聚类使用 EM 算法，因为计算模型参数（均值向量）需要依赖于样本类别的划分（可以理解为隐变量），而样本类别的划分又反过来依赖于模型参数的选取，这就是相互依赖关系，正是因为存在这种关系，所以我们采用 EM 算法迭代更新模型参数和隐变量。

狭义上的隐变量定义在不同书籍或博客中大不一样，但是广义上的隐变量都是指「样本类别的划分结果」，也就是上面描述 EM 算法时提到的。在我们整体把握模型的 EM 算法流程时，将隐变量认为是「样本类别的划分结果」非常有助于理解；但是涉及具体公式时，仍然需要具体问题具体指明。

既然 EM 算法离不开隐变量的计算，那么我们先定义隐变量，即规定如何对样本进行划分。

训练集 $D=\{{xx}_1,{xx}_2,\cdot \cdot \cdot ,{xx}_m\}$ ，令随机变量 $z_j\in \{1,2,\cdot \cdot \cdot ,k\}$ 表示样本 ${xx}_j$ 的高斯混合成分，其取值未知。显然，$z_j$ 的先验概率 $P(z_j=i)$ 对应于 ${\alpha }_i$ $(i=1,2,\cdot \cdot \cdot ,k)$ 。根据贝叶斯定理，$z_j$ 的后验分布对应于
$$\begin{array}{rl}{p}_{\mathcal{M}}(z_j=i\mid {xx}_j)& =\frac{P(z_j=i)\cdot p_{\mathcal{M}}({xx}_j\mid z_j=i)}{p_{\mathcal{M}}({xx}_j)}\\ & =\frac{{\alpha }_i\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^k{\alpha }_l\cdot p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_l)}\end{array}\text{\hspace{1em}(43)}$$

当样本类别已知时， $p_{\mathcal{M}}({xx}_j\mid z_j=i)$ 退化为 $p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)$ ，即确定了样本所属的混合成分，高斯混合分布退化为单高斯分布。

换言之，$p_{\mathcal{M}}(z_j=i\mid {xx}_j)$ 给出了样本 ${xx}_j$ 由第 $i$ 个高斯混合成分生成的后验概率。为方便叙述，将其简记为 ${\gamma }_{ji}$ $(i=1,2,\cdot \cdot \cdot ,k)$ 。

当高斯混合分布式 $(42)$ 已知时，即参数 $(\mu \mu ,\Sigma \Sigma )$ 已知时，高斯混合聚类将把样本集 $D$ 划分为 $k$ 个簇 $\mathcal{C}=\{C_1,C_2,\cdot \cdot \cdot ,C_k\}$，每个样本 ${xx}_j$ 的簇标记 ${\lambda }_j$ 如下确定：
$${\lambda }_j={\mathrm{argmax}}_{i\in \{1,2,\cdot \cdot \cdot ,k\}}{\gamma }_{ji}\text{\hspace{1em}(44)}$$
我们认为后验概率 ${\gamma }_{ji}$ 就是 EM 算法中的隐变量。这主要是因为推导得到的参数更新公式（式 $(47)$、$(48)$ 和 $(51)$）全都可以转换为依赖于后验概率 ${\gamma }_{ji}$ 的形式。

根据式 $(43)$，我们可以通过已知的模型参数 $\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ 计算出隐变量 ${\gamma }_{ji}$ ，对应 EM 算法中的 $\mathrm{E}$ 步。而已知隐变量求解模型参数的 $\mathrm{M}$ 步，给定样本集 $D$，我们采用极大似然估计，即最大化（对数）似然

似然函数可以理解为目标函数或损失函数。

$$\begin{array}{rl}LL(D)& =\ln \left(\prod _{j=1}^m{p}_{\mathcal{M}}({xx}_j)\right)\\ & =\sum _{j=1}^m\ln \left(\sum _{i=1}^k{\alpha }_i\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)\right)\end{array}\text{\hspace{1em}(45)}$$

下面对模型参数更新公式进行推导。

提醒一点，高斯混合分布的模型参数是 $\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ ，即可学习参数，而每个混合成分的参数是 $\{({\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ 。

若模型参数 $\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ 能使式 $(45)$ 最大化，则由 $\frac{\partial LL(D)}{\partial {\mu \mu }_i}=0$ 有
$$\sum _{j=1}^m\frac{{\alpha }_i\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^k{\alpha }_l\cdot p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_l)}({xx}_j-{\mu \mu }_i)=0\text{\hspace{1em}(46)}$$
由式 $(43)$ 以及 ${\gamma }_{ji}=p_{\mathcal{M}}(z_j=i\mid {xx}_j)$，有
$${\mu \mu }_i=\frac{\sum _{j=1}^m{\gamma }_{ji}{xx}_j}{\sum _{j=1}^m{\gamma }_{ji}}\text{\hspace{1em}(47)}$$

另附 ${\mu \mu }_i$ 的求解过程。

即各混合成分的均值可通过样本加权平均来估计，样本权重是每个样本属于该成分的后验概率。类似地，由 $\frac{\partial LL(D)}{\partial {\Sigma \Sigma }_i}=0$ 可得
$${\Sigma \Sigma }_i=\frac{\sum _{j=1}^m{\gamma }_{ji}({xx}_j-{\mu \mu }_i)({xx}_j-{\mu \mu }_i{)}^T}{\sum _{j=1}^m{\gamma }_{ji}}\text{\hspace{1em}(48)}$$

另附 ${\Sigma \Sigma }_i$ 的求解过程。

对于混合系数 ${\alpha }_i$，除了要最大化 $LL(D)$，还需满足 ${\alpha }_i\ge 0$，${\sum }_{i=1}^k{\alpha }_i=1$，考虑 $LL(D)$ 的拉格朗日形式
$$LL(D)+\lambda \left(\sum _{i=1}^k{\alpha }_i-1\right)\text{\hspace{1em}(49)}$$

其中 $\lambda$ 为拉格朗日乘子。由式 $(48)$ 对 ${\alpha }_i$ 的导数为 $0$，有
$$\sum _{j=1}^m\frac{p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^k{\alpha }_l\cdot p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_l)}+\lambda =0\text{\hspace{1em}(50)}$$
式 $(50)$ 两边同乘以 ${\alpha }_i$，对 $k$ 个类别求和，由 ${\sum }_{i=1}^k{\alpha }_i=1$ 有
$$\begin{gathered} \sum _{i=1}^k\sum _{j=1}^m\frac{{\alpha }_i\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^k{\alpha }_l\cdot p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_i)}+\lambda \sum _{i=1}^k{\alpha }_i=0 \\ \sum _{j=1}^m\sum _{i=1}^k\frac{{\alpha }_i\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^k{\alpha }_l\cdot p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_i)}+\lambda =0 \\ m+\lambda =0 \\ \lambda =-m \end{gathered}$$
已知 $\lambda =-m$，式 $(50)$ 两边同乘以 ${\alpha }_i$，有
$${\alpha }_i=\frac{1}{m}\sum _{j=1}^m{\gamma }_{ji}\text{\hspace{1em}(51)}$$

即每个高斯成分的混合系数由样本属于该成分的平均后验概率确定。

这样一来，高斯混合分布的 EM 算法就确定了：在每步迭代中，先根据当前参数和式 $(43)$ 来计算每个样本属于每个高斯成分的后验概率 ${\gamma }_{ji}$ （ $\mathrm{E}$ 步），再根据式 $(47)$、$(48)$ 和 $(51)$ 更新模型参数 $\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ （ $\mathrm{M}$ 步）。

高斯混合聚类算法描述如算法 $3$ 所示。算法第 $1$ 行对高斯混合分布的模型参数进行初始化。然后，在第 $2\sim 12$ 行基于 EM 算法对模型参数进行迭代更新。若 EM 算法的停止条件满足（例如已达到最大迭代轮数，或似然函数 $LL(D)$ 增长很少甚至不再增长），则在第 $14\sim 17$ 行根据高斯混合分布确定簇划分，在第 $18$ 行返回最终结果。

$$\begin{array}{llcccccccccccccccc}\text{输入:}& 样本集D=\{{xx}_1,{xx}_2,,\cdot \cdot \cdot ,{xx}_m\};& & & & & & & & & & & & & & & & \\ & 高斯混合成分个数k;& & & & & & & & & & & & & & & & \\ \text{过程:}& & & & & & & & & & & & & & & & & \end{array}$$

$$\begin{array}{rl}1:& 初始化高斯混合分布的模型参数\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}\\ 2:& \text{repeat}\\ 3:& \text{for}j=1,2,\cdot \cdot \cdot ,m\text{do}\\ 4:& 根据式(43)计算{xx}_j由各混合成分生成的后验概率，即\\ & {\gamma }_{ji}=p_{\mathcal{M}}(z_j=i\mid {xx}_j)(1\le i\le k)\\ 5:& \text{end}\text{for}\\ 6:& \text{for}i=1,2,\cdot \cdot \cdot ,k\text{do}\\ 7:& 计算新均值向量:{\mu \mu }_i^{\prime }=\frac{{\sum }_{j=1}^m{\gamma }_{ji}{xx}_j}{{\sum }_{j=1}^m{\gamma }_{ji}};\\ 8:& 计算新协方差矩阵:{\Sigma \Sigma }_i^{\prime }=\frac{{\sum }_{j=1}^m{\gamma }_{ji}({xx}_j-{\mu \mu }_i)({xx}_j-{\mu \mu }_i{)}^T}{{\sum }_{j=1}^m{\gamma }_{ji}};\\ 9:& 计算新混合系数:{\alpha }_i^{\prime }=\frac{{\sum }_{j=1}^m{\gamma }_{ji}}{m};\\ 10:& \text{end}\text{for}\\ 11:& 将模型参数\{({\alpha }_i,{\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}更新为\{({\alpha }_i^{\prime },{\mu \mu }_i^{\prime },{\Sigma \Sigma }_i^{\prime })\mid 1\le i\le k\}\\ 12:& \text{until}满足停止条件\\ 13:& C_i=\varnothing (1\le i\le k)\\ 14:& \text{for}j=1,2,\cdot \cdot \cdot ,m\text{do}\\ 15:& 根据式(44)确定{xx}_j的簇标记入{\lambda }_j;\\ 16:& 将{xx}_j划入相应的簇:C_{{\lambda }_j}=C_{{\lambda }_j}\bigcup \{{xx}_j\}\\ 17:& \text{end}\text{for}\end{array}$$

$$\begin{array}{lcccccccccccccccccc}\text{输出:}簇划分\mathcal{C}=\{C_1,C_2,\cdot \cdot \cdot ,C_k\}& & & & & & & & & & & & & & & & & & \end{array}$$

算法 3    高斯混合聚类算法

以表 $1$ 的西瓜数据集为例，令高斯混合成分的个数 $k=3$ 。算法开始时，假定将高斯混合分布的模型参数初始化为：${\alpha }_1={\alpha }_2={\alpha }_3=\frac{1}{3}$；${\mu \mu }_1={xx}_6,{\mu \mu }_2={xx}_{22},{\mu \mu }_3={xx}_{27}$；${\Sigma \Sigma }_1={\Sigma \Sigma }_2={\Sigma \Sigma }_3=\left(\begin{array}{cc}0.1& 0.0\\ 0.0& 0.1\end{array}\right)$ 。

在第一轮迭代中，先计算样本由各混合成分生成的后验概率。以 ${xx}_1$ 为例，由式 $(43)$ 算出后验概率 ${\gamma }_{11}=0.219,{\gamma }_{12}=0.404,{\gamma }_{13}=0.377$ 。所有样本的后验概率算完后，得到如下新的模型参数：
$$\begin{gathered} {\alpha }_1^{\prime }=0.361,{\alpha }_2^{\prime }=0.323,{\alpha }_3^{\prime }=0.316 \\ {\mu \mu }_1^{\prime }=(0.491;0.251),{\mu \mu }_2^{\prime }=(0.571;0.281),{\mu \mu }_3^{\prime }=(0.534;0.295) \\ {\Sigma \Sigma }_1^{\prime }=\left(\begin{array}{cc}0.025& 0.004\\ 0.004& 0.016\end{array}\right),{\Sigma \Sigma }_2^{\prime }=\left(\begin{array}{cc}0.023& 0.004\\ 0.004& 0.017\end{array}\right),{\Sigma \Sigma }_1^{\prime }=\left(\begin{array}{cc}0.024& 0.005\\ 0.005& 0.016\end{array}\right) \end{gathered}$$
模型参数更新后，不断重复上述过程，不同轮数之后的聚类结果如图 $9$ 所示。

图 9    高斯混合聚类(k=3)在不同轮数迭代后的聚类结果。其中样本簇 C₁，C₂与C₃中的样本点分别用“○”，“■”与“▲”表示，各高斯混合成分的均值向量用“+”表示。

4.6.6 生成模型

高斯混合模型是一种生成模型，所谓生成模型是指，通过数据集确定模型参数后，可以用于随机生成其他样本的模型。

假设样本的生成过程由高斯混合分布给出：首先，根据 ${\alpha }_1,{\alpha }_2,\cdot \cdot \cdot ,{\alpha }_k$ 定义的先验分布选择高斯混合成分，其中 ${\alpha }_i$ 为选择第 $i$ 个混合成分的概率；然后，根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。

4.6.7 混合系数的意义

先重复一遍上面提到的前两点。

第一点是凑概率密度函数，保证积分值为 $1$，更贴近概率模型。

第二点是用权重表示先验概率，即 ${\alpha }_i$ 表示属于（任何）样本属于第 $i$ 个簇的概率，或者说满足第 $i$ 个混合成分分布的概率，如此便可以将高斯混合分布 $p_{\mathcal{M}}(xx,\mu \mu ,\Sigma \Sigma )$ （更详细准确的模型表达形式，其中 $\mu \mu =({\mu \mu }_1,{\mu \mu }_2,\cdot \cdot \cdot ,{\mu \mu }_k)$ ，$\Sigma \Sigma$ 同理）理解为全概率，即将对样本 $xx$ 在参数为 $(\mu \mu ,\Sigma \Sigma )$ 的模型中出现的概率求解问题转化为了在不同混合成分（参数为 $({\mu \mu }_i,{\Sigma \Sigma }_i)$ 的高斯分布）中样本 $xx$ 出现概率求和的简单问题。这样可以认为是对高斯混合分布函数，即式 $(42)$ 的另一种理解。

第三点是从生成模型的角度来看，当我们引入了先验概率后，生成样本的过程中会先依据先验概率随机选择一个混合成分，再根据混合成分的分布进行采样。如果不引入先验概率，相当于没有提出选择混合分类的方法，或者说选择任何一个混合分类的概率相同，可行但可解释性不如引入先验概率的模型。

第四点，首先明确，即使 ${\sum }_{i=1}^k{\alpha }_i\ne 1$，甚至不定义混合系数，即 ${\alpha }_i=1$ $(1\le i\le k)$ ，都是可行的。下面讨论混合系数全为 $1$ 时的可行性。

当 ${\alpha }_i=1$ $(1\le i\le k)$ 时，高斯混合分布定义为
$$p_{\mathcal{M}}(xx)=\sum _{i=1}^{k}p(xx\mid {\mu \mu }_i,{\Sigma \Sigma }_i)\text{\hspace{1em}(52)}$$

接下来将讨论 ${\alpha }_i=1$ $(1\le i\le k)$ 时的可行性。只要的 EM 算法可行，模型参数就可以更新，模型就是可行的。

• $\mathrm{E}$ 步

  后验概率
  $$p_{\mathcal{M}}(z_j=i\mid {xx}_j)=\frac{P(z_j=i)\cdot p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^{k}p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_l)}\text{\hspace{1em}(53)}$$
  隐变量 $t_{ji}$ 为
  $$t_{ji}=\frac{p_{\mathcal{M}}(z_j=i\mid {xx}_j)}{P(z_j=i)}=\frac{p({xx}_j\mid {\mu \mu }_i,{\Sigma \Sigma }_i)}{\sum _{l=1}^{k}p({xx}_j\mid {\mu \mu }_l,{\Sigma \Sigma }_l)}\text{\hspace{1em}(54)}$$
  根据式 $(54)$ 可以计算出隐变量。

• $\mathrm{M}$ 步

  类似于式 $(47)$ 和 $(48)$ 的推导，可得
  $${\mu \mu }_i=\frac{\sum _{j=1}^m{t}_{ji}{xx}_j}{m}\text{\hspace{1em}(55)}$$

  $${\Sigma \Sigma }_i=\frac{\sum _{j=1}^m{t}_{ji}({xx}_j-{\mu \mu }_i)({xx}_j-{\mu \mu }_i{)}^T}{m}\text{\hspace{1em}(56)}$$

  由于没有混合系数，模型参数只有 $\{({\mu \mu }_i,{\Sigma \Sigma }_i)\mid 1\le i\le k\}$ ，因此不存在更新混合系数的步骤。

观察 EM 算法发现隐变量的计算和模型参数的更新过程都没有问题，说明即使不采用混合系数，高斯混合模型也是可行的。

但是如何对样本进行划分呢？由于我们不知道 $P(z_j=i)$ $(i\le i\le k)$ ，所以虽然能够计算出隐变量 $t_{ji}$，但依然无法根据式 $(54)$ 计算出后验概率 $p_{\mathcal{M}}(z_j=i\mid {xx}_j)$，从而无法对样本进行划分。

以 ${\lambda }_j={\mathrm{argmax}}_{i\in \{1,2,\cdot \cdot \cdot ,k\}}{t}_{ji}$ 作为划分规则是否可以？可以，但是可解释性差。后验概率能明确表达「在已知样本的情况下，样本属于某个分类的概率」，可是 $t_{ji}$ 的含义无法直观理解，也就没有说服性。如果我们想使用后验概率作为划分依据，那么就必须学习先验概率 $P(z_j=i)$ $(i\le i\le k)$ ，如此一来就又变回式 $(42)$ 定义的高斯混合分布了。

以上这四点从可行性和可解释性两个方面对混合系数存在的意义进行说明。对于可解释性，完全可以从更多角度去理解。

4.6.8 与 $k$-means 对比

• 高斯混合模型假设数据点是由具有未知参数的高斯分布的混合生成的，目标是估计高斯分布的参数（$\mu \mu$ 和 $\Sigma \Sigma$），以及来自每个分布的数据点的比例（${\alpha }_i$）；相比之下，$k$-means 聚类不对数据点的潜在分布做出任何假设，只是将数据点划分为 $k$ 个集群，其中每个集群由其质心定义。

• 虽然高斯混合模型更灵活，但它们可能比 $k$-means 更难训练。$k$-means 通常收敛速度更快，因此在运行时是一个重要考虑因素的情况下可能是首选。 一般来说，当数据集较大且聚类分离良好时，$k$-means 会更快、更准确。当数据集较小或聚类分离不充分时，高斯混合模型会更准确。

• 高斯混合模型在簇的形状方面更加灵活，而 $k$-means 仅限于球形簇。

• 高斯混合模型可以处理缺失数据，而 $k$-means 不能。这种差异可以使高斯混合模型在某些应用中更有效，例如具有大量噪声的数据或未明确定义的数据。

• 在 $k$-means方法中使用EM来训练高斯混合模型时对初始值的设置非常敏感。而对比 $k$-means，混合高斯模型有更多的初始条件要设置。实践中不仅初始类中心要指定，而且协方差矩阵和混合系数也要设置。可以运行 $k$-means来生成类中心，并以此作为高斯混合模型的初始条件。