统计机器学习笔记1--AI背景概论,损失函数,风险,,,
摘要
期末来临,平时没怎么整理,听得有些零碎。抽点时间把它从头到尾捋一遍,也方便写综合实验的论文。
文章目录
- 摘要
- 背景
-
- 人工智能(Artificial Intelligence)
- 机器学习
- 数学理解
-
- 常见的损失函数
- 期望损失
-
- 经验风险
- 总结
背景
Q1. 什么是统计机器学习?
人工智能 和 统计学习,机器学习是人工智能的核心。机器学习还包括很流行的深度学习。
人工智能(Artificial Intelligence)
-
定义:研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新兴技术科学。
-
理解:通过模块化人脑,将人脑的功能在机器上实现,做出识别、认知、分析与决策。比如通过实现机器听觉、机器视觉、运动控制、语音识别来是机器具有人类的各类中枢系统。
-
人工智能的三次浪潮:
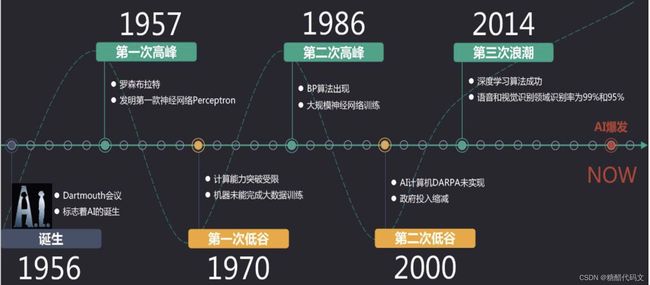
其中,第一次浪潮是由于1957年罗森布莱特发明了感知机,可用于识别图片和文字。过了七年,约瑟夫建立了世界上第一个自然语言对话程序ELIZA,可以通过简单的模式匹配和对话规则与人聊天。在此期间,符号主义占主导地位。核心是知识表示、知识推理、知识运用。接着,由于计算机性能的不足和数据量的严重缺失,导致早期人工智能只能解决少数特定问题,易受干扰,这引发了AI的第一次低谷。80年代引起第二次世界浪潮,这是由于专家系统(是一个具有大量专门知识和经验的程序系统)以及人工神经网络带来了新进展。但由于知识量过多,总结困难,AI迅速进入第二次低谷,此时,台式电脑性能不断提升甚至超过了昂贵的LISP机,科研经费不断被削减。1997年5月11日,IBM的“深蓝”战胜了国际象棋冠军某某外国人,引发热议。直到2011年,多层神经网络为基础的深度学习大幅超越传统算法,被推广到多个应用领域。而后,AI逐渐转向机器人与人结合而成的增强型智能系统。
机器学习
- Tom Mitchell(1998)这么概括机器学习:一个程序被认为能从经验 E 中学习,解决任务 T,达到性能度量值P,当且仅当,有了经验 E 后,经过 P 评判,程序在处理 T 时的性能有所提升。
- 分类:
- 有监督学习(Supervised)
观测数据中同时又有预测变量 X i X_i Xi和响应变量 Y i Y_i Yi。例如:线性回归模型。
其中,当响应变量 Y i Y_i Yi为连续型(定量)变量时,称为回归;当响应变量 Y i Y_i Yi为定性型变量时,称为分类; - 无监督学习(Unsupervised)
观测数据中,没有观测响应变量 Y i Y_i Yi的值。需通过预测变量内部所具有的特征或结构信息来预测Y。 - 半监督学习(Semi-Supervised)
观测数据中,存在少部分带有响应变量 Y i Y_i Yi的观测值。 - 强化学习 (Reinforcement)
略。
数学理解
-
目标:找到一个函数 Y = f ( x ) Y=f(x) Y=f(x),用来进行预测和推断。
-
如何估计该函数:
- 模型:一般分为参数(Parametric)模型和非参数(Non-Parametric)模型。前者需要对模型实现做出一些关于数据的分布以及模型形式的假定,估计模型参数后得到模型。模型参数越多的模型,模型复杂度越高。
- 策略:损失函数(Loss Function)或风险函数(期望损失),用于评价模型的好坏。前者表示一次预测的好坏,后者表示平均意义下模型预测的好坏。
- 算法:确定模型的具体计算步骤。
常见的损失函数
- 0-1损失函数
L ( Y , f ( X ) ^ ) = { 1 , Y ≠ f ( X ) ^ 0 , Y = f ( X ) ^ L(Y,\hat{f(X)})=\left\{ \begin{aligned} 1 & , & Y\neq\hat {f(X)} \\ 0 & , & Y=\hat {f(X)} \end{aligned} \right. L(Y,f(X)^)=⎩⎨⎧10,,Y=f(X)^Y=f(X)^
- 平均损失函数
L ( Y , f ( X ) ^ ) = ( Y − f ^ ( X ) ) 2 L(Y,\hat{f(X)})=(Y-\hat f(X))^2 L(Y,f(X)^)=(Y−f^(X))2 - 绝对损失函数
L ( Y , f ( X ) ^ ) = ∣ Y − f ^ ( X ) ∣ L(Y,\hat{f(X)})=|Y-\hat f(X)| L(Y,f(X)^)=∣Y−f^(X)∣ - 对数似然损失函数
L ( Y , P ( Y ∣ X ) ) = − l o g P ( Y ∣ X ) L(Y,P(Y|X))=-logP(Y|X) L(Y,P(Y∣X))=−logP(Y∣X)
期望损失
损失函数的期望,又称风险函数:
R e x p ( f ^ ) = E p [ L ( Y , f ( X ) ^ ) ] = ∫ z × y L ( Y , f ( X ) ^ ) P ( x , y ) d x d y R_{exp}(\hat f)=E_p[L(Y,\hat {f(X)})]=\int_{z\times y}{L(Y,\hat {f(X)})P(x,y)}dxdy Rexp(f^)=Ep[L(Y,f(X)^)]=∫z×yL(Y,f(X)^)P(x,y)dxdy
但是 P ( x , y ) P(x,y) P(x,y)分布函数,一般不知道。所以有
经验风险
由大数定律来估计期望风险,
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } R e x p ( f ^ ) = 1 N ∑ i = 1 N L ( Y , f ( X ) ^ ) T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\\ R_{exp}(\hat f)=\frac{1}{N}\sum_{i=1}^{N} L(Y,\hat {f(X)}) T={(x1,y1),(x2,y2),...,(xN,yN)}Rexp(f^)=N1i=1∑NL(Y,f(X)^)
上式称为经验风险最小化最优模型。当样本容量过小时,可能会产生过拟合(Overfitting)现象。为此,引入结构风险最小化。即加入正则化项(Regularizer)或惩罚项(Penalty term) J ( f ) J(f) J(f):
R e x p ( f ^ ) = 1 N ∑ i = 1 N L ( Y , f ( X ) ^ ) + λ J ( f ) R_{exp}(\hat f)=\frac{1}{N}\sum_{i=1}^{N} L(Y,\hat {f(X)})+\lambda J(f) Rexp(f^)=N1i=1∑NL(Y,f(X)^)+λJ(f)
总结
本质上,我们要使机器得到一个函数,函数的形式选择多种多样,算法也不尽相同,但都要能实现我们的需求。再通过一些评价指标和精度控制,来不断修正优化我们的模型(参数),得到更好的模型效果,机器也能更好地完成复杂任务。