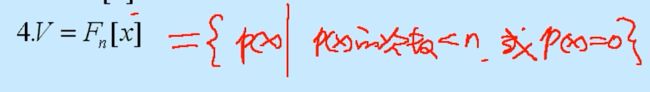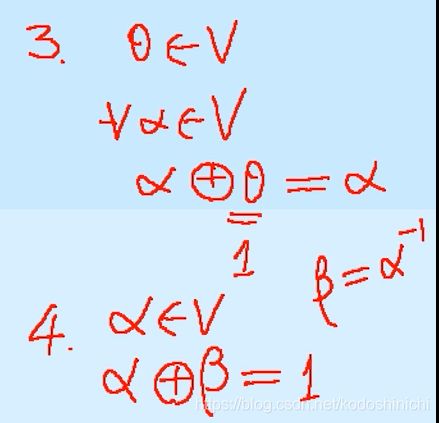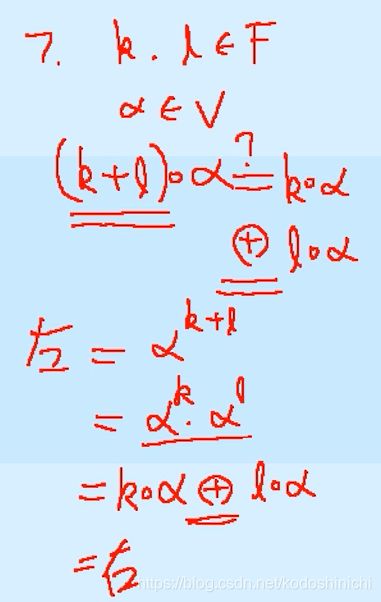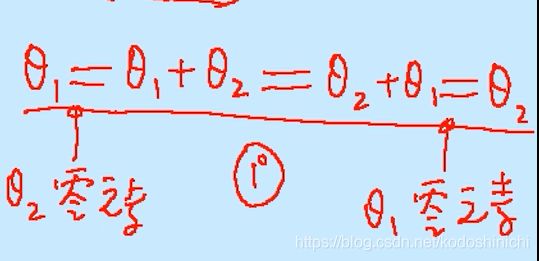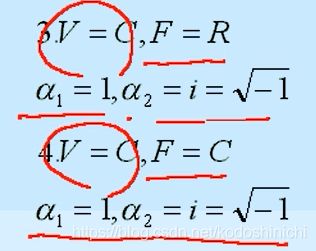【矩阵论】线性空间与线性变换（1）

线性空间与线性变换

---

#1 线性空间的定义

目录

• 线性空间的形式化定义
• 常见的线性空间举例
• 非线性空间反例举例
• 线性空间的性质汇总
• 线性相关性及其结论

在数学中，尤其是代数中，人们常常喜欢把“运算规律相同”的物体归为一类进行讨论，从而就提出了各种各样的【代数系统】的概念。

比较常见的代数系统：群、环、域
线性空间也是其中一个较为常见的代数系统。

1. 线性空间的形式化定义
   ①首先先定义一个集合（代数系统）
   需要一个非空集合和一个数域
   

对于上面定义的集合，在集合上又定义了两个运算（加法和数乘），注意上面的表达还需要满足“封闭性”。也即：集合内的两个元素进行加法和数乘运算的结果也需要在集合中才行。

②再关于上述两种运算定义一些性质

满足下述运算性质的集合就可以成为线性空间，线性空间这个集合内的元素就可以称为向量。

性质1——加法满足交换律
性质2——加法满足结合律
性质3——需要存在零元素
性质4——需要存在负元素
【以上四条性质均为针对加法运算而言】
p.s. 上述的零元素和负元素，均是针对某一集合定义的某一运算而言的，符合相应的定义即可，并不意味着零元素的数值一定是实数0.
性质5——元素1和任意元素的乘积都等于元素本身
性质6——数乘系数的结合性
性质7——数乘运算对系数和具有分配律
性质8——数乘运算对元素和具有分配律
【后四条性质是针对数乘运算而言的】

2. 常见的线性空间举例
   ①数域空间上的n维向量集合——V = Fⁿ

对于这样一个n维向量，既可以理解为行向量，又可以理解为列向量。

②数域空间上的n维方阵集合——V = F^nxn

③系数在数域F中关于x的多项式的全体——V = F[x]

④系数在数域F中关于x的多项式的部分集合——V = Fn[x]

也就是，系数在数域F中关于x的多项式集合中，只有那些次数小于n或者全零多项式才能包含在该集合中。

讲到这个集合的时候可以自己在心里验证一下，在这个系统上定义的数乘和加法运算是否具有封闭性。

⑤V = C，F = R

按照前文中关于线性空间的定义，集合V直接取的就是全体复数，复数的加法一定是满足性质的，而复数也可以和实数进行数乘运算，且运算的结果也具有封闭性、结合性和分配律。

⑥V = C，F = C

同理，复数的加法，复数和复数的乘法同样可以构成一个线性空间。

⑦再来看一个非典型的线性空间例子

指定了相应的元素集合V和数域F，同时为了使这个集合具有线性空间的性质，自己对加法和数乘运算进行了重新定义。

以下会对线性空间的性质进行验证，读者可以体会一下所谓“零元素”和“负元素”为什么是针对具体的集合和运算而言的。

【验证】

性质1和2：数乘的交换律和结合律↔加法的交换律和结合律

性质3：零元素——存在一个θ元素，该元素和任意元素的加法运算得到的为原元素本身
性质4：负元素——存在一个β元素，任意元素和该元素的加法

根据上图的推导，对于我们自己定义的数乘和加法运算而言，零元素是数字1，负元素是某一元素的倒数。

性质7：数乘运算对系数的分配律。
如下图的推导过程，有一个点要记住【自我提醒！！】系数的加法是通常意义上的加法，但是分配之后的加法是定义的加法。

3. 非线性空间反例举例

通常对于非线性空间进行判定时，只需要找到一个反例即可。
而找反例的突破口就是从线性空间的定义和性质两个方面来入手——其一就是要验证加法和数乘运算的封闭性；其二就是要验证线性空间的运算性质是否都满足。

①V = R，F = C

不满足数乘封闭性

②V = R⁺，F = R，通常运算

说明：注明的【通常运算】意味着在该集合上定义的数乘和加法运算就是我们通常意义上所见到的数乘和加法运算。

同样不满足数乘封闭性

4. 线性空间的性质汇总

假设V是数域F上的线性空间，则

①V中的零向量是唯一的

证明思路：在数学中碰到“唯一性”证明都会想到使用反证法，假设存在两个元素θ1和θ2均是零向量，那么最后需要能够推出该两个元素是相等的。
证明的依据就是选用线性空间定义中的几条公理和性质。

利用零元素的性质（任何元素加上零元素都等于它自身），当θ2是零元素的时候，θ1 = θ1+θ2；当θ1是零元素的时候，也有θ2=θ1+θ2，根据等式传递性从而得证θ1 = θ2.

②对于V中的任意一个元素α，α的负元素是唯一的，记为-α

思路讲解（从左到右，从上到下共有7个等号）按照等号的顺序和意义进行说明
等号1：零元素的定义
等号2：负元素的定义（某个元素和其负元素的和等于零元素）
等号3：加法的结合性
等号4：加法的交换性
等号5：负元素的定义（题目假设了β1和β2都是α的负元素）
等号6：加法的交换律
等号7：零元素的定义
最终根据等式可得到β1 = β2

③加法消去律

注意在证明的时候，要始终记得我们所处的背景是线性空间，只定义了两类运算，而且也只有有限的定理可以使用。

证明：等式两边同时加上α的负元素即可。

④向量方程的解

虽然在我们常用的代数系统中解上述方程，只要移项就可以得到相应的解。但是在向量空间这样一个新定义出来的线性系统，我们只定义了数乘和加法运算，不能想当然去解，只能用已知的性质来理解。

理解：两边同时加上α的负元素，就可以得到向量方程的解x = β - α

⑤数乘运算和负运算的可交换性（自己起的名字，非官方）

⑥零元素相关的性质

---

回想一下我们在线性代数这门课程中学习到的有关向量的一些概念，比如线性相/无关，线性组合，无关向量组等等，这些概念的提出本质上就是基于数乘和加法运算。
现在类比我们在实数域范围定义的线性空间，在给定的数乘和加法运算下，我们同样也可以得到相关的概念。

5. 线性相关/无关及其性质

（1）线性相关/线性无关的定义

（2）线性相关性的相关性质

①【一组线性相关的向量，存在某一个向量，可以由其余的向量线性表示出来】

证明与理解
上述结论是一个充要条件，在证明时需要分别从充分性和必要性分别去证明。
<必要性>

因为存在某一个不为零的系数，可以利用前面讨论的线性空间的运算性质，将某个向量对应地进行求解表示。
<充分性>
充分性，就是已知某一个向量可以由其他向量线性表示，那么必然存在一个为1（或者是-1）的系数，就满足“不全部为0的系数”这一条件，故必然是线性相关的。

②线性相关与线性表示的关系

③向量组的极大线性无关性

通过该定理可以说明，任意一个向量组的两个极大线性无关组中应该含有相同个数的向量，向量的个数就被称为向量组的秩

【推论】-反映两个向量组之间的线性关系与向量组的向量个数之间的关系

（3）例题

①证明向量组的线性无关（相关）性

注意，这之后我们讨论的线性空间都是广义的线性空间，比如这一道题中，每一个向量是一个2维方阵

• 对于线性相关性的有关证明，方法论就是先假设存在一系列系数，对向量组中的各个向量进行线性组合结果为0，然后去推导是否所有系数均为0.即，都是根据线性相关和线性无关的定义去判定。
• 上述E11 E12 E21 E22 这四个向量组成的向量组是线性无关的，所以这四个向量均被称作是矩阵单位。

②证明向量组的线性相关性

思路上同，按照定义进行列写再展开，从而将验证多项式向量组是否线性相关的问题 转换成 验证下面这个三阶三次的齐次方程组是否具有非零解。
有非零解，则线性相关。

③不同F和V的取值对于向量组线性相关性的影响

在题3中，因为F = R，所以系数要从F，也即R集合中取，故α1和α2都是线性无关的。

在题4中，因为F = C，所以系数要从C中取，当a = i,b = -1时，aα1+bα2 = 0就成立了，且此时a和b并不是全0，所以此时两个向量是线性相关的。

④数乘和加法的不同定义对于向量组线性相关性的影响

【直接截取的老师的板书，有点凌乱，请见谅】
回顾一下上文中我们自己定义的一个特殊的线性空间，数乘表示乘幂，加法表示乘法的一个线性空间。

当我们按照线性相关的定义书写k1α1+k2α2+…+knαn = 0这样的式子，不仅要注意系数从哪个集合中取，还要注意其中的加法和数乘运算都可能是自己定义出来的。
按照上述的运算，列写的两个向量2和3是线性相关的。