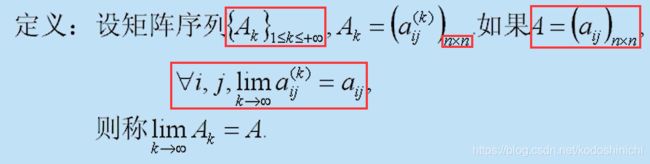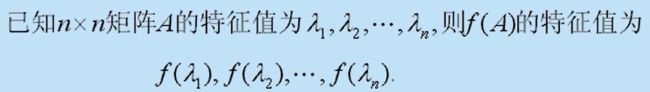【矩阵论】范数和矩阵函数（2）

范数及矩阵函数之收敛性与矩阵函数

定义矩阵的范数是为了讨论矩阵的收敛性。
注：范数和矩阵函数这个系列的（1）（2）等划分是按照章节来的，与视频的分集并不完全一致。

一. 收敛定理

1. 按坐标收敛

2. 按范数收敛

在《【矩阵论】范数和矩阵函数（1）》中我们已经讨论过范数的定义，以及按照范数收敛的定义，如下。

3. 等价性

对于一个矩阵序列来说，按照坐标收敛和按照范数收敛，其二者具有等价的意义。

---

有很多可能的矩阵序列，就我们讨论的意义来说，幂序列和矩阵幂级数是我们最关心的两类矩阵序列。

二. 幂序列

对于给定的方阵A，考虑方阵列{A^k}

1. 定理1

（1）定理描述

（2）定理证明
按照矩阵范数的角度来进行证明，根据矩阵的相容性可以对||A^k||放缩成||A||^k。
因为||A||<1，所以在k→∞的趋近下，该值趋近于O。

2. 定理2

（1）定理描述

一个矩阵序列趋近于O的充要条件是这个矩阵的谱半径小于1.

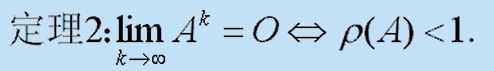
（2）定理证明

[1]：对于任意一个方阵A，存在可逆矩阵P，使得A变成一个Jordan标准形矩阵，从而可以将A的幂乘矩阵用可逆矩阵P和Jordan形矩阵J进行表示。

在《【矩阵论】矩阵的相似标准型（4）》中“一.2.”部分，我们对每个矩阵的Jordan形矩阵的存在性和唯一性进行了讨论。

[2]：求解在k→0时，A^k的逼近趋势；因为P是确定的可逆矩阵，P≠O，只需要验证在k→0时，J^k是否逼近于O。
又因为J是一个分块对角矩阵，根据分块对角矩阵的幂乘运算特性，相当于各个分块元素J_i进行幂乘运算。

[3]：每一个J_i矩阵都是一个Jordan块，是一个上三角矩阵，对其进行幂乘运算，就相当于各个元素进行幂乘运算。
要想J^k→O，则J_i^k(i=1,2…,n)→O，那么J_i^k中的各个元素λ_i^k就应该趋近于零。
每个特征值k次幂乘在k→∞时逼近于0，则特征值的模长应该小于1，从而明晰矩阵A的谱半径小于1.

证毕。

3. 定理3

通过定理1和定理2，不难推测矩阵范数和谱半径之间也一定存在某种关系。

（1）定理描述

（2）定理证明

以下只做简要说明：

对于矩阵A，任取其一个特征值λ_i，则与该特征值相对应的某个特征向量即为η_i，根据特征量的定义有Aη_i = λ_iη_i

对于上述等式，两边同时求矩阵范数，则有**||Aη_i|| =** ||λ_iη_i|| = ||λ_i||·||η_i||
又因为该矩阵范数时相容的，所以根据相容性的定义可得：||Aη_i||≤||A||·||η_i||

因为η_i≠θ(特征向量的要求)，所以**||η_i||>0**，上述不等式两边同时约掉||η_i||
则可得，||λ_i||≤||A||。

因为λ_i是A任取的一个特征值，说明矩阵A任意一个特征值的模长都小于矩阵A的矩阵范数，故ρ(A)≤||A||

---

三. 矩阵幂级数

1. 矩阵幂级数定义及其收敛性

通过矩阵序列（幂级数的部分和）的收敛性来定义矩阵幂级数的收敛性。

2. 定理

---

上文部分以及该系列的第(1)篇文章，都是我们为了讨论矩阵函数及其收敛性所做的准备工作，以下我们将开始讨论矩阵函数。

四. 矩阵函数

1. 矩阵函数的定义

核心要义：通过将函数展开成级数，借助矩阵多项式的运算，把矩阵函数转换成相应的矩阵级数来讨论。

（1）定义描述

（2）常见的矩阵函数

记住重要的矩阵函数，关键在于记住重要的函数级数。
p.s. 以下三个级数的收敛半径都是无穷大，这意味着不论矩阵A的谱半径为多少，其相应的函数e^A,sinA和cosA都是有意义的。

2. Jordan块的函数

根据上述的定义，对于一些简单的或者高阶幂乘有特点的矩阵，可以快速求解其矩阵函数。
但是对于一些更加一般的矩阵，我们也希望找到求解函数的方法。

因为任意一个矩阵都有其对应的Jordan标准形，而且Jordan形也是上三角矩阵，具有一定的特殊性，于是我们从研究Jordan块的函数入手，来解决一般矩阵函数的求解问题。

（1）Jordan块的多项式函数

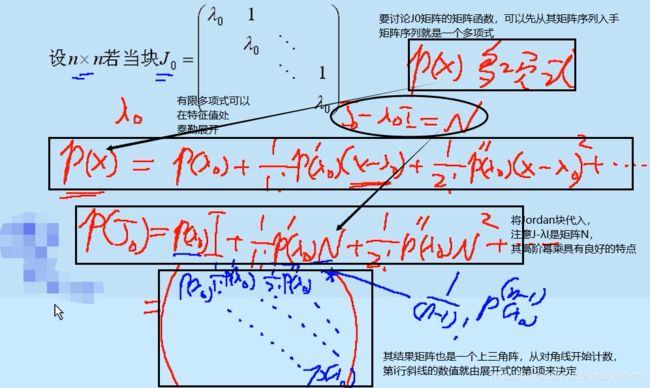
（2）Jordan块的任意解析式函数
先给出结论：上文最后得到的那个矩阵形式，不仅对于多项式函数成立，对于任意解析式函数也有同样的结果。

本质：从多项式函数到任意函数的过渡，可以借助部分和与无穷级数之间的关系。

3. Jordan形矩阵的函数

同样延续上面的思路，得到Jordan形矩阵的函数，就是对矩阵各个对角块上的Jordan块分别代入函数即可。

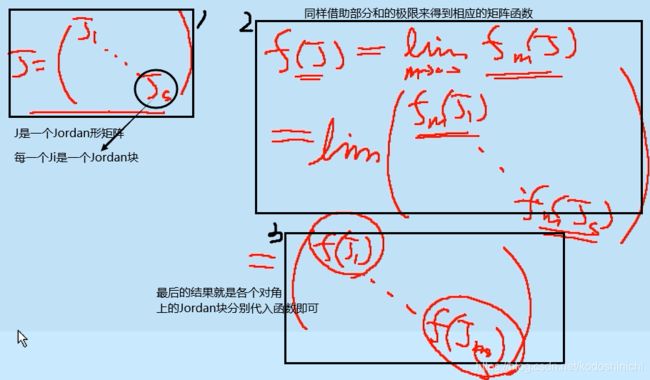
4. 一般矩阵的矩阵函数

在讨论Jordan块和Jordan形矩阵时，我们已经梳理了思路，任何矩阵都有其对应的Jordan形，所以可以把Jordan形的结论应用在一般矩阵的函数求解上。

（1）定理1

【定理证明】
假设现在有一个解析函数f(x) = lim f_m(x)，以及有一个一般矩阵A，且已知P^-1AP = J（J就是A对应的Jordan标准形），即A可以表示成A = PJP^-1；

那么可知f(A) = lim f_m(A) = lim P（f_m(J)）^-1P^-1

因为f_m(x)是个多项式函数，而P矩阵在这里是确定的常量矩阵，所以将A代入f_m(x)相当于只把J代入多项式函数中。

根据极限运算，f(A) = p(lim f_m(J))P^-1 = Pf(J)P^-1

因为P矩阵是关于下标m的不变量，因此关于m求极限的时候，P矩阵可以直接提出不参与极限运算。

（2）定理2

这个定理在线性代数课程中对于多项式函数f已经验证过是成立的，此处只不过将f推广到任意解析式函数。

也可以借助前面的定理来理解，已知f(A) = Pf(J)P^-1，所以f(A)和f(J)肯定是相似的，具有相同的特征值。

而J是Jordan标准形，f(J)依然是上三角矩阵，其主对角线上的元素就是其特征值，而对角线上的元素，也就是将数值代入f函数中计算后得到的结果（根据Jordan块和Jordan标准形的函数可知）。

（3）待定系数法

按照前面将任意矩阵化简成Jordan标准形的思路，虽然可行，但是求解Jordan矩阵和与之对应的变换矩阵计算量太大。
因此，我们有以下名为“待定系数法”的方法

证明：

关于Jordan形和最小多项式的定理细节部分可以参考博文《【矩阵论】矩阵的相似标准型（4）（5）》

基于上述的思路，可能原本函数f是一个形式十分复杂的函数，接下来我们只需要构造一个多项式函数g，满足定理中的若干约束即可。
也就是可设g(x) = a₀+a₁x+…+a_p-1x^p-1，那么按照定理中的约束，即可得到p个方程进行系数求解。
p.s. 这里还要注意p = Σrⁱ-1（也就是最小多项式的总次数-1）

5. 矩阵函数的计算示例

（1）利用定义进行计算（适合高阶幂有特点的矩阵）


（2）Jordan形矩阵的函数计算

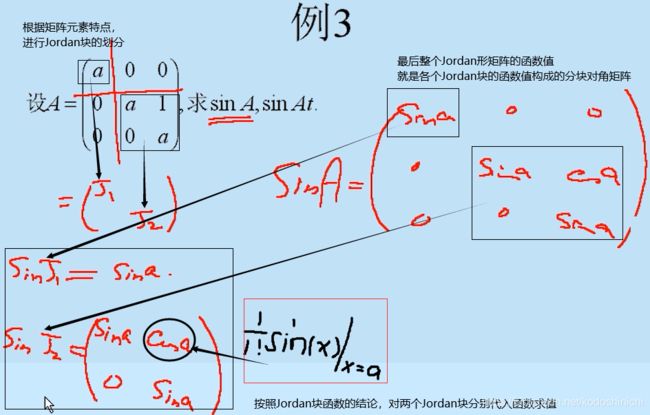
同理，要求解sinAt，相当于解析式函数从sinx变成了sinxt，求解思路完全一致，答案见下方。

（3）一般矩阵的函数计算

要想利用上文讨论的定理，借助Jordan标准形的函数结果来求得一般矩阵的函数，就需要先求解出矩阵A对应的Jordan标准形J以及相应的变换矩阵P。

根据矩阵的特征量信息来确定Jordan标准形的形式，可以参考以下博文，其中有例题讲解。
《【矩阵论】矩阵的相似标准型（4）（5）》

下面使用待定系数法求解一般矩阵的函数值。

【求解过程】
其中当f(A) = e^At时，求解思路与上述一致，只是代入方程组求解出来的系数a和b不同而已，答案应为g(A) = f(A) = (1-t)e^tI+te^tA.

---

五. 矩阵函数的性质

1. 性质描述

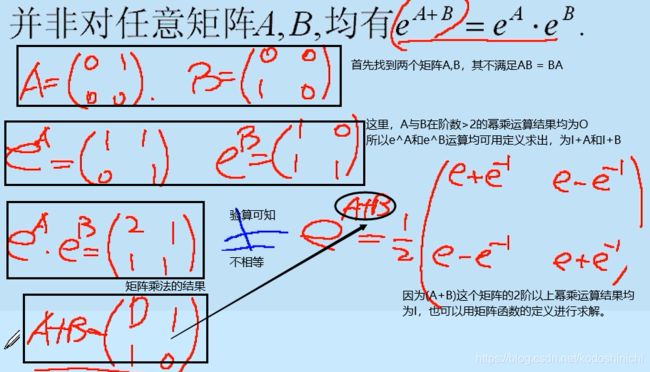
p.s.上图中性质2处的表述应该是“则e^AB = e^BA = e^A+B”,截图时忘记修改，望读者注意。

2. 性质证明
①性质1直接利用矩阵函数的定义，将自然常数e进行级数展开，将零矩阵O代入，即可得到相应结果。

②将e^AB和e^A+B项都分别按照级数展开，然后讨论其中的一般项A^kB^l项的系数，两边都对应相等，所以两个式子也相等。

P.S. 上述证明过程中，能够用组合式来求解某一般项A^kB^l的系数，是使用了二项式定理，而该定理的成立是基于两个项A和B是可交换的。

那么若A和B是不可交换的，我们可以通过举反例来说明此时性质2不再成立。

③在定理描述部分已经进行了证明，参考上上图。

---

应用上述性质，可以简化矩阵函数的计算过程。

【例】矩阵函数的计算