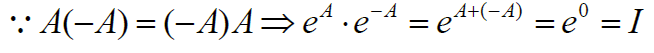【矩阵论】3. 矩阵运算与函数——矩阵函数
10.1 常见解析函数
10.1.1 Taylor级数
引入参数
10.1.2 正弦级数
引入参数
10.1.3 余弦级数
10.1.4 一些约定
a. A为0阵
b. 奇偶性
c. 单位阵
e t I = e t I , s i n ( t I ) = s i n ( t ) I , c o s ( t I ) = c o s ( t ) I e^{tI}=e^tI,sin(tI)=sin(t)I,cos(tI)=cos(t)I etI=etI,sin(tI)=sin(t)I,cos(tI)=cos(t)I
d. 转置穿脱
( e A ) H = e A H (e^{A})^H=e^{A^H} (eA)H=eAH
e. H阵
A H = A , 则 e i A 为 U 阵 , 即 ( e i A ) H = ( e i A ) − 1 , 或 ( e i A ) H e i A = I A H = − A , 则 e A 为 U 阵 , 即 ( e A ) H = ( e A ) − 1 , 或 ( e A ) H e A = I A^H=A,则 e^{iA}为U阵,即 (e^{iA})^H=(e^{iA})^{-1},或(e^{iA})^He^{iA}=I\\ A^H=-A,则 e^{A}为U阵,即 (e^{A})^H=(e^{A})^{-1},或(e^{A})^He^{A}=I AH=A,则eiA为U阵,即(eiA)H=(eiA)−1,或(eiA)HeiA=IAH=−A,则eA为U阵,即(eA)H=(eA)−1,或(eA)HeA=I
10.2 欧拉公式
e x e^x ex 与 c o s x cosx cosx 和 s i n x sinx sinx 的关系
e i A = c o s A + i s i n A , e − A = c o s A − i s i n A , i = − 1 c o s A = 1 2 ( e i A + e − i A ) , s i n A = 1 2 i ( e i A − e − i A ) \begin{aligned} &e^{iA}=cosA+isinA,e^{-A}=cosA-isinA,i=\sqrt{-1}\\ &cosA=\frac{1}{2}(e^{iA}+e^{-iA}),sinA=\frac{1}{2i}(e^{iA-e^{-iA}}) \end{aligned} eiA=cosA+isinA,e−A=cosA−isinA,i=−1cosA=21(eiA+e−iA),sinA=2i1(eiA−e−iA)
引入参数
e i t x = c o s ( t x ) + i s i n ( t x ) , e − i t x = c o s ( t x ) − i s i n ( t x ) e i t A = c o s ( t A ) + i s i n ( t A ) , e − i t A = c o s ( t A ) − i s i n ( t A ) \begin{aligned} e^{itx}=cos(tx)+isin(tx),e^{-itx}=cos(tx)-isin(tx)\\ e^{itA}=cos(tA)+isin(tA),e^{-itA}=cos(tA)-isin(tA) \end{aligned} eitx=cos(tx)+isin(tx),e−itx=cos(tx)−isin(tx)eitA=cos(tA)+isin(tA),e−itA=cos(tA)−isin(tA)
10.3 e A e^A eA
10.3.1 e A e^A eA 运算
a. 交换公式
若 A B = B A 可 交 换 , 则 有 交 换 公 式 e A ⋅ e B = e A + B = e B ⋅ e A 若 A B ≠ B A , 则 交 换 公 式 不 成 立 若AB=BA可交换,则有交换公式e^A\cdot e^B=e^{A+B} =e^B\cdot e^A\\ 若AB\neq BA,则交换公式不成立 若AB=BA可交换,则有交换公式eA⋅eB=eA+B=eB⋅eA若AB=BA,则交换公式不成立
若满足交换公式,则有
( A + B ) 2 = A 2 + 2 A B + B 2 ( A + B ) 3 = A 3 + 3 A 2 B + 3 A B 2 + B 3 \begin{aligned} &(A+B)^2=A^2+2AB+B^2\\ &(A+B)^3=A^3+3A^2B+3AB^2+B^3 \end{aligned} (A+B)2=A2+2AB+B2(A+B)3=A3+3A2B+3AB2+B3
SP
e A ⋅ e − A = e − A e A = I e^A\cdot e^{-A}=e^{-A}e^A=I eA⋅e−A=e−AeA=I
b. 可逆公式
任一方阵A都有 e A e^A eA 可逆,且 ( e A ) − 1 = e − A (e^A)^{-1}=e^{-A} (eA)−1=e−A
引入参数
( e t A ) − 1 = e − t A (e^{tA})^{-1}=e^{-tA} (etA)−1=e−tA ,且 e t A e − t A = I e^{tA}e^{-tA}=I etAe−tA=I
eg:证明 s i n 2 A + c o s 2 A = I sin^2A+cos^2A=I sin2A+cos2A=I
由 欧 拉 公 式 c o s A = 1 2 ( e i A + e − i A ) , s i n A = 1 2 i ( e i A − e − i A ) , c o s 2 A = 1 4 ( e 2 i A + 2 e i A − i A + e − 2 i A ) = 1 4 ( e 2 i A + 2 e 0 + e − 2 i A ) , s i n 2 A = − 1 4 ( e 2 i A − 2 e 0 + e − 2 i A ) s i n 2 A + c o s 2 A = 1 2 e 0 + 1 2 e 0 = I \begin{aligned} &由欧拉公式 cosA=\frac{1}{2}(e^{iA}+e^{-iA}),sinA=\frac{1}{2i}(e^{iA}-e^{-iA}),\\ &cos^2A=\frac{1}{4}(e^{2iA}+2e^{iA-iA}+e^{-2iA})=\frac{1}{4}(e^{2iA}+2e^0+e^{-2iA}),sin^2A=-\frac{1}{4}(e^{2iA}-2e^0+e^{-2iA})\\ &sin^2A+cos^2A=\frac{1}{2}e^0+\frac{1}{2}e^0=I \end{aligned} 由欧拉公式cosA=21(eiA+e−iA),sinA=2i1(eiA−e−iA),cos2A=41(e2iA+2eiA−iA+e−2iA)=41(e2iA+2e0+e−2iA),sin2A=−41(e2iA−2e0+e−2iA)sin2A+cos2A=21e0+21e0=I
10.3.2 e A e^A eA 特根公式
设方阵A特根 λ ( A ) = { λ 1 , ⋯ , λ n } \lambda(A)=\{\lambda_1,\cdots,\lambda_n\} λ(A)={λ1,⋯,λn} ,则 e A e^A eA 特根为 λ ( e A ) = { e λ 1 , e λ 2 , ⋯ , e λ n } \lambda(e^A)=\{e^{\lambda_1},e^{\lambda_2},\cdots,e^{\lambda_n}\} λ(eA)={eλ1,eλ2,⋯,eλn}
10.3.3 e A e^A eA 行列式
令 n 阶 方 阵 A = ( a i j ) , 则 f ( A ) = e A 的 行 列 式 为 : ∣ e A ∣ = ∏ e λ ( A ) = e ∑ λ i = e t r ( A ) 由 行 列 式 可 知 e t r ( A ) ≠ 0 , 所 以 e A 一 定 可 逆 \begin{aligned} &令n阶方阵A=(a_{ij}),则f(A)=e^A的行列式为:\\ &\vert e^A\vert=\prod e^{\lambda(A)} = e^{\sum \lambda_i}=e^{tr(A)}\\ &由行列式可知 e^{tr(A)} \neq 0,所以e^A一定可逆 \end{aligned} 令n阶方阵A=(aij),则f(A)=eA的行列式为:∣eA∣=∏eλ(A)=e∑λi=etr(A)由行列式可知etr(A)=0,所以eA一定可逆
10.3.4 一些特殊矩阵 e A e^A eA 可求
a. 幂等阵
若 A 2 = A A^2=A A2=A ,则有 e i A = I + ( e t − 1 ) A e^{iA}=I+(e^t-1)A eiA=I+(et−1)A
第一列与第二列每个元素绝对值差1的,很有可能是幂等阵
eg
A 2 = ( 1 0 1 0 ) ( 1 0 1 0 ) = ( 1 0 1 0 ) = A , B 2 = ( 1 0 − 1 0 ) ( 1 0 − 1 0 ) = ( 1 0 − 1 0 ) = B 为 幂 等 阵 可 知 e t A = I + t A + ( t A ) 2 2 ! + ( t A ) 3 3 ! + ⋯ + ( t A ) n n ! = I + [ t + ( t ) 2 2 ! + ( t ) 3 3 ! + ⋯ + ( t ) n n ! ] A = I + ( e t − 1 ) A 同 理 , 可 得 e t B = I + ( e t − 1 ) B \begin{aligned} &A^2=\left( \begin{matrix} 1&0\\1&0 \end{matrix} \right)\left( \begin{matrix} 1&0\\1&0 \end{matrix} \right)=\left( \begin{matrix} 1&0\\1&0 \end{matrix} \right)=A,B^2=\left( \begin{matrix} 1&0\\-1&0 \end{matrix} \right)\left( \begin{matrix} 1&0\\-1&0 \end{matrix} \right)=\left( \begin{matrix} 1&0\\-1&0 \end{matrix} \right)=B为幂等阵\\ &可知 e^{tA}=I+tA+\frac{(tA)^2}{2!}+\frac{(tA)^3}{3!}+\cdots+\frac{(tA)^n}{n!}=I+[t+\frac{(t)^2}{2!}+\frac{(t)^3}{3!}+\cdots+\frac{(t)^n}{n!}]A\\ &=I+(e^t-1)A\\ &同理,可得e^{tB}=I+(e^t-1)B \end{aligned} A2=(1100)(1100)=(1100)=A,B2=(1−100)(1−100)=(1−100)=B为幂等阵可知etA=I+tA+2!(tA)2+3!(tA)3+⋯+n!(tA)n=I+[t+2!(t)2+3!(t)3+⋯+n!(t)n]A=I+(et−1)A同理,可得etB=I+(et−1)B
A 2 = A , 则 e A = I + ( e t − 1 ) A = ( 1 0 0 1 ) + ( e t − 1 ) ( 2 − 2 1 − 1 ) = ( e t − 1 − 2 e t + 2 e t − 1 2 − e t ) \begin{aligned} A^2=A,则e^A=I+(e^t-1)A=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)+(e^t-1)\left( \begin{matrix} 2&-2\\1&-1 \end{matrix} \right)=\left( \begin{matrix} e^t-1&-2e^t+2\\e^t-1&2-e^t \end{matrix} \right) \end{aligned} A2=A,则eA=I+(et−1)A=(1001)+(et−1)(21−2−1)=(et−1et−1−2et+22−et)
b. 对角阵
对角阵 D = ( λ 1 ⋱ λ n ) D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right) D=⎝⎛λ1⋱λn⎠⎞ ,则 f ( D ) = ( f ( λ 1 ) ⋱ f ( λ n ) ) f(D)=\left(\begin{matrix}f(\lambda_1)&&\\&\ddots&\\&&f(\lambda_n)\end{matrix}\right) f(D)=⎝⎛f(λ1)⋱f(λn)⎠⎞
令函数 f ( x ) = e t A ( t 为 参 数 ) = ∑ k = 0 ∞ ( t x ) k k ! f(x)=e^{tA}(t为参数)=\sum_{k=0}\limits^\infty\frac{(tx)^k}{k!} f(x)=etA(t为参数)=k=0∑∞k!(tx)k ,则 f ( D ) = e t D = ∑ k = 0 ∞ ( t D ) k k ! f(D)=e^{tD}=\sum_{k=0}\limits^\infty\frac{(tD)^k}{k!} f(D)=etD=k=0∑∞k!(tD)k
sp
D = ( λ 1 ⋱ λ n ) , 则 e t D = ( e t λ 1 ⋱ e t λ n ) \begin{aligned} &D=\left( \begin{matrix} \lambda_1&&\\&\ddots&\\&&\lambda_n \end{matrix} \right),则e^{tD}=\left( \begin{matrix} e^{t\lambda_1}&&\\&\ddots&\\&&e^{t\lambda_n} \end{matrix} \right) \end{aligned} D=⎝⎛λ1⋱λn⎠⎞,则etD=⎝⎛etλ1⋱etλn⎠⎞
eg
∵ A + B = ( 2 0 ) 为 对 角 阵 ⇒ e A + B = ( e 2 e 0 ) = ( e 2 1 ) \begin{aligned} \because A+B=\left( \begin{matrix} 2&\\&0 \end{matrix} \right)为对角阵\Rightarrow e^{A+B}=\left( \begin{matrix} e^2&\\&e^0 \end{matrix} \right)=\left( \begin{matrix} e^2&\\&1 \end{matrix} \right) \end{aligned} ∵A+B=(20)为对角阵⇒eA+B=(e2e0)=(e21)
c. 单阵
单阵A有谱分解
A = λ 1 G 1 + ⋯ + λ k G k , 且 f ( A ) = f ( λ 1 ) G 1 + ⋯ + f ( λ k ) G k , 其 中 f ( x ) = c 0 + c 1 + x + ⋯ + c k x k + ⋯ A=\lambda_1G_1+\cdots+\lambda_kG_k,且f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k,\\ 其中f(x)=c_0+c_1+x+\cdots+c_kx^k+\cdots A=λ1G1+⋯+λkGk,且f(A)=f(λ1)G1+⋯+f(λk)Gk,其中f(x)=c0+c1+x+⋯+ckxk+⋯
计 算 可 得 λ ( A ) = { i , − i } , A 是 单 阵 , 对 于 任 意 解 析 函 数 f ( x ) 有 谱 公 式 : f ( A ) = f ( i ) G 1 + f ( − i ) G 2 其 中 , G 1 = A − λ 2 I λ 1 − λ 2 = 1 2 i ( i 1 − 1 i ) , G 2 = A − λ 1 I λ 2 − λ 1 = − 1 2 i ( − i 1 − 1 − i ) = 1 2 i ( i − 1 1 i ) 令 f ( x ) = e t x , 则 f ( i ) = e t i , f ( − i ) = e − t i ∴ e t A = e t i G 1 + e − t i G 2 = e t i 2 i ( i 1 − 1 i ) + e − t i 2 i ( i − 1 1 i ) = ( e t i + e − t i 2 e t i − e − t i 2 i − e t i − e − t i 2 i e t i + e − t i 2 ) = ( c o s t s i n t − s i n t c o s t ) \begin{aligned} &计算可得\lambda(A)=\{i,-i\},A是单阵,对于任意解析函数f(x)有谱公式:f(A)=f(i)G_1+f(-i)G_2\\ &其中,G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{2i}\left( \begin{matrix} i&1\\-1&i \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=-\frac{1}{2i}\left( \begin{matrix} -i&1\\-1&-i \end{matrix} \right)=\frac{1}{2i}\left( \begin{matrix} i&-1\\1&i \end{matrix} \right)\\ &令f(x)=e^{tx},则f(i)=e^{ti},f(-i)=e^{^{-ti}}\\ &\therefore e^{tA}=e^{ti}G_1+e^{-ti}G_2=\frac{e^{ti}}{2i}\left( \begin{matrix} i&1\\-1&i \end{matrix} \right)+\frac{e^{-ti}}{2i}\left( \begin{matrix} i&-1\\1&i \end{matrix} \right)=\left( \begin{matrix} \frac{e^{ti}+e^{-ti}}{2}&\frac{e^{ti}-e^{-ti}}{2i}\\ -\frac{e^{ti}-e^{-ti}}{2i}&\frac{e^{ti}+e^{-ti}}{2} \end{matrix} \right)=\left( \begin{matrix} cost&sint\\-sint&cost \end{matrix} \right) \end{aligned} 计算可得λ(A)={i,−i},A是单阵,对于任意解析函数f(x)有谱公式:f(A)=f(i)G1+f(−i)G2其中,G1=λ1−λ2A−λ2I=2i1(i−11i),G2=λ2−λ1A−λ1I=−2i1(−i−11−i)=2i1(i1−1i)令f(x)=etx,则f(i)=eti,f(−i)=e−ti∴etA=etiG1+e−tiG2=2ieti(i−11i)+2ie−ti(i1−1i)=(2eti+e−ti−2ieti−e−ti2ieti−e−ti2eti+e−ti)=(cost−sintsintcost)
A 是 行 和 矩 阵 , 故 λ ( A ) = { 5 , t r ( A ) − 5 } = { 5 , − 2 } , A 有 两 个 互 异 特 征 根 , 故 A 为 单 阵 , 有 谱 分 解 f ( A ) = f ( 5 ) G 1 + f ( − 2 ) G 2 , 其 中 G 1 = A − λ 2 I λ 1 − λ 2 = 1 7 ( 3 4 3 4 ) , G 2 = I − G 1 = 1 7 ( 4 − 4 − 3 3 ) 令 f ( x ) = e t x , 则 f ( 5 ) = e 5 t , f ( − 2 ) = e − 2 t ∴ e t A = e 5 t G 1 + e − 2 t G 2 = e 5 t 7 ( 3 4 3 4 ) + e − 2 t 7 ( 4 − 4 − 3 3 ) = 1 7 ( 3 e 5 t + 4 e − 2 t 4 e 5 t − 4 e − 2 t 3 e 5 t + 4 e − 2 t 4 e 5 t − 4 e − 2 t ) ∣ e t A ∣ = e t r ( t A ) = e 3 t ( e ( t A ) ) − 1 = e − t A , 即 将 t 替 换 为 − t 即 可 , e − t A = 1 7 ( 3 e − 5 t + 4 e 2 t 4 e − 5 t − 4 e 2 t 3 e − 5 t + 4 e 2 t 4 e − 5 t − 4 e 2 t ) \begin{aligned} &A是行和矩阵,故\lambda(A)=\{5,tr(A)-5\}=\{5,-2\},A有两个互异特征根,故A为单阵,有谱分解\\ &f(A)=f(5)G_1+f(-2)G_2,其中G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{7}\left( \begin{matrix} 3&4\\3&4 \end{matrix} \right),G_2=I-G_1=\frac{1}{7}\left( \begin{matrix} 4&-4\\-3&3 \end{matrix} \right)\\ &令f(x)=e^{tx},则f(5)=e^{5t},f(-2)=e^{-2t}\\ &\therefore e^{tA}=e^{5t}G_1+e^{-2t}G_2=\frac{e^{5t}}{7}\left( \begin{matrix} 3&4\\3&4 \end{matrix} \right)+\frac{e^{-2t}}{7}\left( \begin{matrix} 4&-4\\-3&3 \end{matrix} \right)=\frac{1}{7}\left( \begin{matrix} 3e^{5t}+4e^{-2t}&4e^{5t}-4e^{-2t}\\ 3e^{5t}+4e^{-2t}&4e^{5t}-4e^{-2t}\\ \end{matrix} \right)\\ &\vert e^{tA}\vert=e^{tr(tA)}=e^{3t}\\ &(e^{(tA)})^{-1}=e^{-tA},即将t替换为-t即可,e^{-tA}=\frac{1}{7}\left( \begin{matrix} 3e^{-5t}+4e^{2t}&4e^{-5t}-4e^{2t}\\ 3e^{-5t}+4e^{2t}&4e^{-5t}-4e^{2t}\\ \end{matrix} \right) \end{aligned} A是行和矩阵,故λ(A)={5,tr(A)−5}={5,−2},A有两个互异特征根,故A为单阵,有谱分解f(A)=f(5)G1+f(−2)G2,其中G1=λ1−λ2A−λ2I=71(3344),G2=I−G1=71(4−3−43)令f(x)=etx,则f(5)=e5t,f(−2)=e−2t∴etA=e5tG1+e−2tG2=7e5t(3344)+7e−2t(4−3−43)=71(3e5t+4e−2t3e5t+4e−2t4e5t−4e−2t4e5t−4e−2t)∣etA∣=etr(tA)=e3t(e(tA))−1=e−tA,即将t替换为−t即可,e−tA=71(3e−5t+4e2t3e−5t+4e2t4e−5t−4e2t4e−5t−4e2t)
通 过 特 征 方 程 ∣ A − λ I ∣ 计 算 得 λ ( A ) = { − 2 , 1 , 1 } , 且 A − I = ( 3 6 0 − 3 − 6 0 − 3 − 6 0 ) , r ( A − I ) = 3 − 2 = 1 ∴ A 为 单 阵 , 有 谱 分 解 f ( A ) = f ( 1 ) G 1 + f ( − 2 ) G 2 令 f ( x ) = e t x , f ( 1 ) = e t , f ( − 2 ) = e − 2 t , G 1 = A − λ 2 I λ 1 − λ 2 = 1 3 ( A + 2 I ) = ( 2 2 0 − 1 − 1 0 − 1 − 2 1 ) , G 2 = I − G 1 = ( − 1 − 2 0 1 2 0 1 2 0 ) 代 入 得 e t A = e t G 1 + e − 2 t G 2 = e t ( 2 2 0 − 1 − 1 0 − 1 − 2 1 ) + e − 2 t ( − 1 − 2 0 1 2 0 1 2 0 ) = ( 2 e t − e − 2 t 2 e t − 2 e − 2 t 0 e − 2 t − e − t 2 e − 2 t − e t 0 e − 2 t − e t 2 e − 2 t − 2 e t e t ) 令 t = 1 , 可 得 e A = ( 2 e − e − 2 2 e − 2 e − 2 0 e − 2 − e − 1 2 e − 2 − e 0 e − 2 − e 2 e − 2 − 2 e e ) ∣ e A ∣ = e t r ( A ) = e 0 = 1 \begin{aligned} &通过特征方程\vert A-\lambda I\vert计算得\lambda(A)=\{-2,1,1\},且A-I=\left( \begin{matrix} 3&6&0\\-3&-6&0\\-3&-6&0 \end{matrix} \right),r(A-I)=3-2=1\\ &\therefore A为单阵,有谱分解 f(A)=f(1)G_1+f(-2)G_2\\ &令f(x)=e^{tx},f(1)=e^{t},f(-2)=e^{-2t},G_1=\frac{A-\lambda_2 I}{\lambda_1-\lambda_2}=\frac{1}{3}(A+2I)=\left( \begin{matrix} 2&2&0\\-1&-1&0\\-1&-2&1 \end{matrix} \right),G_2=I-G_1=\left( \begin{matrix} -1&-2&0\\1&2&0\\1&2&0 \end{matrix} \right)\\ &代入得e^{tA}=e^tG_1+e^{-2t}G_2=e^t\left( \begin{matrix} 2&2&0\\-1&-1&0\\-1&-2&1 \end{matrix} \right)+e^{-2t}\left( \begin{matrix} -1&-2&0\\1&2&0\\1&2&0 \end{matrix} \right)=\left( \begin{matrix} 2e^t-e^{-2t}&2e^t-2e^{-2t}&0\\ e^{-2t}-e^{-t}&2e^{-2t}-e^t&0\\ e^{-2t}-e^t&2e^{-2t}-2e^t&e^t \end{matrix} \right)\\ &令t=1,可得e^A=\left( \begin{matrix} 2e-e^{-2}&2e-2e^{-2}&0\\ e^{-2}-e^{-1}&2e^{-2}-e&0\\ e^{-2}-e&2e^{-2}-2e&e \end{matrix} \right)\\ &\vert e^A\vert = e^{tr(A)}=e^{0}=1 \end{aligned} 通过特征方程∣A−λI∣计算得λ(A)={−2,1,1},且A−I=⎝⎛3−3−36−6−6000⎠⎞,r(A−I)=3−2=1∴A为单阵,有谱分解f(A)=f(1)G1+f(−2)G2令f(x)=etx,f(1)=et,f(−2)=e−2t,G1=λ1−λ2A−λ2I=31(A+2I)=⎝⎛2−1−12−1−2001⎠⎞,G2=I−G1=⎝⎛−111−222000⎠⎞代入得etA=etG1+e−2tG2=et⎝⎛2−1−12−1−2001⎠⎞+e−2t⎝⎛−111−222000⎠⎞=⎝⎛2et−e−2te−2t−e−te−2t−et2et−2e−2t2e−2t−et2e−2t−2et00et⎠⎞令t=1,可得eA=⎝⎛2e−e−2e−2−e−1e−2−e2e−2e−22e−2−e2e−2−2e00e⎠⎞∣eA∣=etr(A)=e0=1
d. 幂0阵
A k = 0 A^k=0 Ak=0 ,则A为幂0阵
( 1 ) A 2 = ( 1 − 1 1 − 1 ) ( 1 − 1 1 − 1 ) = 0 , 由 幂 等 公 式 A 2 = 0 , 则 e t A = I + t A + A 2 2 ! + ⋯ = I + t A + 0 + ⋯ = I + t A = ( 1 + t − t t 1 − t ) s i n ( t A ) = t A − ( t A ) 3 3 ! + ⋯ = t A = ( t − t t − t ) c o s ( t A ) = I − t 2 A 2 2 ! = I = ( 1 0 0 1 ) t = − t 时 , 可 得 ( e t A ) − 1 = e ( − t ) A = ( 1 − t t − t 1 + t ) \begin{aligned} &(1)\\ &A^2=\left( \begin{matrix} 1&-1\\1&-1 \end{matrix} \right)\left( \begin{matrix} 1&-1\\1&-1 \end{matrix} \right)=0,由幂等公式A^2=0,则\\ &e^{tA}=I+tA+\frac{A^2}{2!}+\cdots=I+tA+0+\cdots=I+tA=\left( \begin{matrix} 1+t&-t\\t&1-t \end{matrix} \right)\\ &sin(tA)=tA-\frac{(tA)^3}{3!}+\cdots=tA=\left( \begin{matrix} t&-t\\t&-t \end{matrix} \right)\\ &cos(tA)=I-\frac{t^2A^2}{2!}=I=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)\\ &t=-t时,可得(e^{tA})^{-1}=e^{(-t)A}=\left( \begin{matrix} 1-t&t\\-t&1+t \end{matrix} \right) \end{aligned} (1)A2=(11−1−1)(11−1−1)=0,由幂等公式A2=0,则etA=I+tA+2!A2+⋯=I+tA+0+⋯=I+tA=(1+tt−t1−t)sin(tA)=tA−3!(tA)3+⋯=tA=(tt−t−t)cos(tA)=I−2!t2A2=I=(1001)t=−t时,可得(etA)−1=e(−t)A=(1−t−tt1+t)