跟我一起学PyTorch-04:神经网络
本节从神经网络的发展着手,依次介绍激活函数、前向算法、损失函数、反向传播算法以及PyTorch中的数据处理,最后使用PyTorch解决一个iris数据集上的多分类问题。通过本节的学习,我们将对整个神经网络的流程有一个比较全面的认识。
1.神经元与神经网络
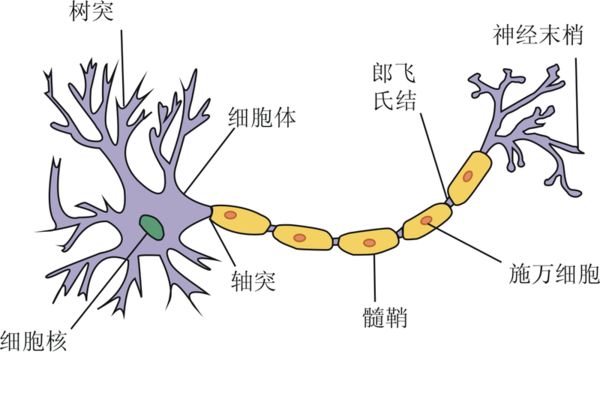
神经元最早是生物学上的概念,它是人脑中的最基本单元。人脑中含有大量的神经元,米粒大小的脑组织中就包含超过10000个神经元,不同的神经元之间相互连接,每个神经元与其他的神经元平均有6000个连接。一个神经元接收其他神经元传递过来的信息,通过某种方式处理后再传递给其他神经元。下图就是生物神经元的示意图。
一个神经元由细胞核、树突、轴突和轴突末梢等组成。其中树突有很多条,且含有不同的权重,主要用来接收从其他神经元传来的信息;接收到的信息在细胞整合后产生新的信息传递给其他神经元;而轴突只有一条,轴突末端有许多神经末梢,可以给其他神经元传递信息。神经末梢跟其他神经元的树突连接,从而传递信号,这个链接的位置在生物学上叫做“突触”。
在对人脑工作机理研究的基础上,1943年McCulloch和Pitts参考了生物神经元的结构,最早提出了人工神经元模型,即MP神经元模型。MP神经元从外部或者其他神经元接受输入信息,通过特定的计算得到输出结果。如下图所示,输入X1,X2,对应权重w1,w2,偏置b,通过加权求和代入f(z)函数中,得到输出Y。这个函数f(z)就是激活函数。人工神经元是人工神经网络中最基本的单元。
MP模型虽然简单,但却是构建神经网络的基础。神经网络(Neural Network,NN)是人工神经网络(Artificial Neural Network,ANN)的简称,由很多神经元组成。神经网络是对人脑工作机制的一种模仿。在MP模型中,权重的值都是预先设置的,因此不能学习。1949年Hebb提出了Hebb学习率,认为人脑神经细胞的突触上的强度是可以变化的。于是研究者开始考虑使用调整权值的方法来让机器学习。
1958年,Rosenblatt提出了由两层(输入层和输出层)神经元组成的神经网络,名叫“感知机”,如下图所示。从结构上,感知机把神经元中的输入变成了单独的神经元,成为输入单元。与神经元模型不同,感知机中的权重是通过训练得到的。感知机类似一个逻辑回归模型,可以做线性分类任务,是首个可以学习的人工神经网络。这为后面的学习算法奠定了基础,可以说感知机是神经网络的基石。但由于它只有一层功能神经单元,因此学习能力非常有限。Minsky在1969年出版了一本名为“Perceptron”的书,使用数学方法详细地证明了感知机的弱点,尤其是感知机对XOP(异或)这样的简单分类任务都无法解决。
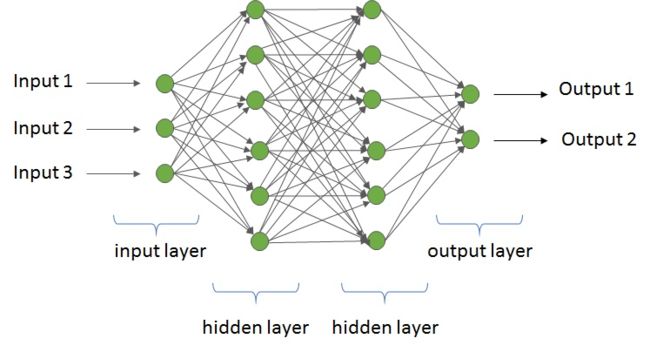
感知机是前馈神经网络的一种,前馈神经网络实最早起也是最简单的一种人工神经网络。前馈神经网络包含多个神经元,被安排在不同的层,即输入层、隐含层、输出层,其中隐含层的个数有0个或多个。在前馈神经网络中,信息在神经元上的传播方向只有一个——向前,即从输入层经过隐含层到达 输出层,神经元之间没有循环结构。感知机就是没有隐含层的前馈神经网络。拥有一个或多个隐含层的前馈神经网络称为“多层感知机”(Multi Layer Perceotron,MLP),如下图所示。
多层感知机可以很好地解决非线性可分问题,我们通常将多层感知机这样的多层结构称为神经网络。
所谓神经网络的训练或者学习,其主要目的就是通过学习算法得到神经网络解决指定问题所需的参数。这里的参数包括各层神经元之间的连接权重以及偏置等。参数的确定需要神经网络通过训练样本和学习算法来迭代找到最优参数组合。说起神经网络的学习算法,不得不提其中最杰出、最成功的代表——反向传播算法。
2.激活函数
前面提到过在神经元中,输入信息通过一个非线性函数y=f(x)产生输出,这个函数决定哪些信息保留以传递给后面的神经元,这个函数就是激活函数(Activation Function),又被称为非线性函数(Nonlinearity Function),对于给定的输入,激活函数执行固定的数学运算得到输出结果,根据输出结果控制输入信息的保留程度。
激活函数要具有以下性质:
- 非线性:当激活函数是线性时,一个两层的神经网络基本上就可以表达所有的函数了,恒等函数f(x)=x不满足这个条件,如果MLP中使用恒等激活函数,那么整个神经网络跟单层的神经网络是等价的。为什么需要非线性呢?因为线性的叠加还是线性,而线性函数的表达能力有限,只能做线性可分的任务。对于线性不可分的更复杂的问题,比如说playground上的一些问题,线性不可分,所以需要用到非线性激活函数。
- 连续可微性:在训练神经网络的过程中,使用到了梯度下降,所以连续可微性是必要的。ReLU虽然不连续,但是也同样适合做激活函数。
- 值域是有限的:激活函数的值域是有限的时候,基于梯度下降的训练过程才能越来越稳定,因为特征表示受有限值的影响更加有效。
- 单调性:激活函数是单调的时候,单层的神经网络才能保证是凸函数。
- 具有单调导数的光滑函数:在某些情况下,这些已经被证明可以更好地概括。对这些性质的论证表名,这种激活函数与奥卡姆剃刀原理(简单有效原理)更加一致。
- 函数值和输入近似相等:满足这个条件的激活函数,当权重初始化成很小的随机数时,神经网络的训练将会很高效,如果不满足这个条件则需要很小心的初始化神经网络权重。
下面介绍几种常见的激活函数:Sigmoid、Tanh、Hard Tanh、ReLU、Softmax、LogSoftmax等。
1.Sigmoid
Sigmoid是一种很常用的非线性函数,其公式如下:
f ( x ) = δ ( x ) = 1 1 + e − x f(x)=\delta(x)=\frac{1}{1+e^{-x}} f(x)=δ(x)=1+e−x1
因其形状像S,又称S函数,将输入变量映射到(0,1)之间,对于特别大的输入,其输出结果是1;对于特别小的输入,其输出结果是0。早期在各类任务中应用广泛,但是现在只在某些特定的场合使用,因为它有自身的缺点:
- 梯度消失:从图形上可以看出,但输入变量特别大或者特别小的时候,函数曲线变化趋于平缓,也就是说函数的梯度变得越来越小,直到接近于0。这会导致经过神经元的信息很少。
- 非0均值:输出值不是0均值的,这样在后面的神经元上将得到非0均值的输入。如果进入神经元的数据时正的,在反向传播中权重上的梯度也永远是正的。这会导致权重梯度的更新呈现锯齿形态,这是不可取的。通过batch的权重和可能最终会得到不同的符号,可以得到缓解。比起梯度消息,这个问题不那么严重。
- 计算量大:因为其函数求导涉及除法,在神经网络的反向传播求梯度时,计算量很大。
PyTorch中Sigmoid的定义为torch.nn.Sigmoid,对输入的每个元素执行Sigmoid函数,输出的维度和输入的维度相同:
>>> import torch
>>> import torch.nn as nn
>>> import torch.autograd as autograd
>>> input_data = autograd.Variable(torch.randn(2))
>>> print(input_data)
tensor([-0.3765, 1.1710])
>>> m = nn.Sigmoid()
>>> print(m(input_data))
tensor([0.4070, 0.7633])
2.Tanh
Tanh是一个双曲三角函数,其公式如下:
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
从图像上可以看出,Tanh与Sigmoid不同,它将输入变量映射到(-1,1)之间,它是Sigmoid函数经过简单的变换得到的:
t a n h ( x ) = 2 δ ( 2 x ) − 1 tanh(x)=2\delta(2x)-1 tanh(x)=2δ(2x)−1
Tanh是0均值的,这一点要比Sigmoid好,所以实际应用中效果也会比Sigmoid好,但是它仍然没有解决梯度消失的问题,这点可以从图像上很清楚地看出来。
PyTorch中Tanh的定义:torch.nn.Tanh。输出的维度和输入的维度也是相同的:
>>> input_data = autograd.Variable(torch.randn(2))
>>> print(input_data)
tensor([ 0.5413, -0.8901])
>>> Tanh = nn.Tanh()
>>> print(Tanh(input_data))
tensor([ 0.4940, -0.7114])
注意:由于梯度消失的原因,不推荐在隐含层使用Sigmoid和Tanh函数,但是可以在输出层使用;如果有必要使用它们的时候,记住:Tanh要比Sigmoid好,因为Tanh是0均值的。
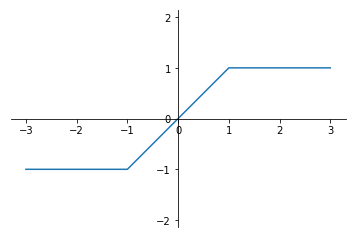
3.Hard Tanh
和Tanh类似,Hard Tanh同样把输入变量映射到(-1,1)之间,不同的是,映射的时候不再是通过公式计算,而是通过给定的阈值直接到达最终结果。标准的Hard Tanh把所有大于1的输入变成1,所有小于-1的输入变成-1,其他的输入不变:
KaTeX parse error: Unknown column alignment: * at position 39: … \begin{array}{*̲*lr**} …
PyTorch中Hard Tanh支持指定阈值min_val和max_val,以改变输出的最小值和最大值,比如说对于f=Hardtanh(-2,2)的输出,所有大于2的输入的输出都是2,所有小于-2的输入的输出都是-2,其他原样输出。
>>> input_data = autograd.Variable(torch.randn(2))
>>> print(input_data)
tensor([ 0.2704, -1.3050])
>>> Hardtanh = nn.Hardtanh()
>>> print(Hardtanh(input_data))
tensor([ 0.2704, -1.0000])
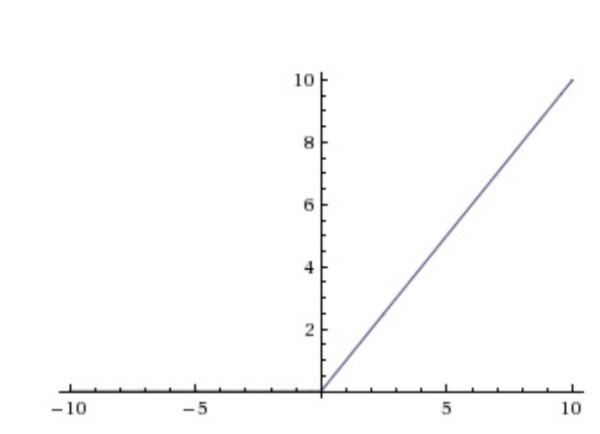
4.ReLU
线性整流函数(Rectified Linear Unit,ReLU)又称为修正线性单元。ReLU是一个分段函数,其公式如下:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
ReLU做的事情很简单,大于0的数原样输出,小于0的数输出0。ReLU在0点处虽然连续不可导,但是也同样适合做激励函数。
ReLU的优点如下:
- 相对于Sigmoid、Tanh而言,ReLU更简单,只需要设置一个阈值就可以计算结果,不用复杂的运算。
- ReLU在随机梯度下降的训练中收敛会更快,原因是ReLU是非饱和的(non-saturating)。
ReLU在很多任务中都有出色的表现,是目前应用广泛的激活函数。但是它也不是十分完美的:ReLU单元很脆弱,以至于在训练过程中可能出现死亡现象,即经过一段时间的训练,一些神经元不再具有有效性,只会输出0,特别是使用较大的学习率的时候。如果发生这种情况,神经元的梯度将永远是0,不利于训练。
一个很大的梯度流过ReLU神经元,权重更新后,神经元就不会再对任何数据有效,如果这样,经过这个点的梯度将永远是0。也就是说,在训练过程中,ReLU单元会不可逆的死亡。如果学习率设置得太高,网络中会有40%可能是死亡的,即整个训练数据集中没有激活的神经元。设置一个合适的学习率可以减少这种情况的发生。
PyTorch中的ReLU函数有一个inplace参数,用于选择是否进行覆盖运算,默认为False。在PyTorch中应用ReLU:
>>> input_data = autograd.Variable(torch.randn(2))
>>> print(input_data)
tensor([ 0.8689, -1.1169])
>>> ReLU = nn.ReLU()
>>> print(ReLU(input_data))
tensor([0.8689, 0.0000])
ReLU的成功应用是在生物学的研究上。生物学研究表明:生物神经不是对所有的外界信息都做出反应,而是部分,即对一部分信息进行忽略,对应于输入信息小于0的情况。
5.ReLU的扩展
为了解决ReLU函数存在的问题,研究者提出了在ReLU基础上的优化方案。在基于ReLU的扩展中,主要思路是当输入是小于0的值时,不再一味地输出0,而是通过一个很小的斜率α的直线方程计算结果,根据α取值的不同可以分为以下几种方案。
(1)Leaky ReLU
使用参数α决定泄露(leak)的程度,就是输入值小于0时直线的斜率,α是固定的取值,而且很小,一般取值为0.01。这样可以保证在输入信息小于0的时候也有信息通过神经元,神经元不至于死亡。
Leaky ReLU函数公式为:
KaTeX parse error: Unknown column alignment: * at position 42: … \begin{array}{*̲*lr**} …
其中,α是一个很小的常数,比如α=0.01。
在PyTorch中,Leaky ReLU有两个参数:
- negative_slope:控制负斜率的角度,即公式中的alpha,默认值是1e-2。
- inplace:选择是否进行覆盖运算,默认值为False。
(2)Parametric ReLU
对于输入的每一个元素运用函数PReLU(x)=max(0,x)+α*min(0,x),这里的α是自学习的参数。当不带参数的调用时,nn.PReLU()在所有输入通道中使用同样的参数α;如果用nn.PReLU(nChannels)调用,α将应用到每个输入:
KaTeX parse error: Unknown column alignment: * at position 51: … \begin{array}{*̲*lr**} …
(3)Randomized ReLU
这是Leaky ReLU的random版本,即参数α是随机产生的,RReLU是在Kaggle的NDSB比赛中首次被提出的,其核心思想就是:在训练过程中,α是从一个高斯分布U(l,u)中随机生成的,然后在测试过程中进行修正。
以上三种ReLU扩展的比较:(这里的a_i就是α)
- ReLU,对小于0部分,直接置为0;
- Leaky ReLU,对小于0部分,进行这样的转换:y_i=a_i * x_i ,它的a_i是固定的;
- PReLU中的a_i 根据数据变化而变化;
- RReLU中的a_i是一个在一个给定的范围内随机抽取的值,这个值在测试环节就会固定下来。
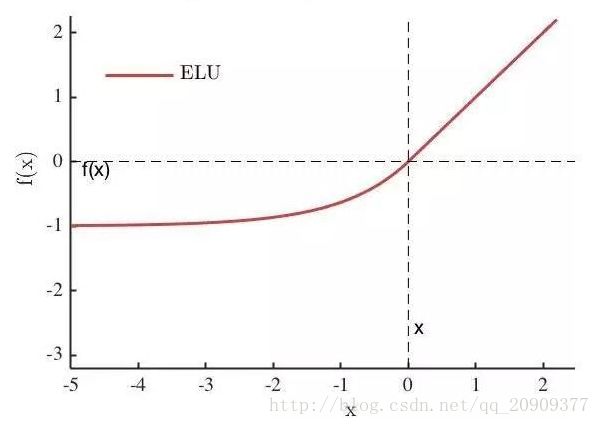
(4)Exponential Linear Unit(ELU)
这是一个新的激活函数,效果比所有的ReLU的变形都要好,训练用的时间少,而且测试指标高。
KaTeX parse error: Unknown column alignment: * at position 55: … \begin{array}{*̲*lr**} …
关于ELU中参数α的选择,通常设置为1,当然也可以在实际应用中尝试其他的值,而且整个函数是平滑的,在x=0会加速梯度下降,因为在x=0处不用跳跃。
其缺点是,因为使用了指数,计算比ReLU系列的计算速度慢,但是训练时收敛快。
(5)Maxout
Maxout是Ian J.Goodfellow在2013年提出的。Maxout和Dropout结合后,在MNIST、CIFAR-10、CIFAR-100、SVHN这4个数据集上都取得了start-of-art的识别率。前面介绍的激活函数都是作用于输入信息的一个元素,输入信息之间是无关的。Maxout单元不是作用于每个元素的函数g(x),而是将x划分成具有k个值的组,然后输出其中一组最大的元素。Maxout有很强的拟合能力,在足够多隐藏层的情况下可以拟合任意的凸函数。
它具有ReLU函数的优点(不会饱和,计算简单),却没有ReLU函数的缺点(容易死亡),它的唯一缺点就是每个神经元都有k个权重,导致权重的总数大大增加。
PyTorch中还没有Maxout的实现,如果想尝试使用,可以参考一下PyTorch在GitHub上的一个例子。
6.Softmax
Softmax函数又称为归一化指数函数,是Sigmoid函数的一种推广。它能将一个含有任意实数的 K K K维向量 z z z压缩到另一个 K K K维向量 σ ( z ) \sigma(z) σ(z)中,返回的是每个互斥输出类别上的概率分布,使得每个元素的范围都在(0,1)之间,并且所有元素的和为1。公式如下:
f ( x i ) = e x p ( x i ) ∑ j e x p ( x j ) f(x_i)=\frac{exp(x_i)}{\sum_{j}exp(x_j)} f(xi)=∑jexp(xj)exp(xi)
跟数学中的max函数相比,max函数取一组数中的最大值,这样会导致较小的值永远不会被取到。Softmax很自然地表示具有K个可能值的离散随机变量的概率分布,所以可以用作一种开关,其中越大的数概率也就越大,Softmax和Maxout一样不是作用于单个神经网络中的每个x值,对n维输入张量运用Softmax函数,将张量的每个元素缩放到(0,1)之间,并且各个输出的和为1。Softmax一般用在网络的输出层,比如在多分类的输出值表示属于每个种类的概率。
PyTorch中关于Softmax的定义:
class torch.nn.Softmax(dim=None)
它接收一个dim参数,以指定计算Softmax的维度,在给定的维度上各个输出的和为1。例如:如果输入的是一个二维张量,dim=0时,表示按列计算Softmax值,每一列上的和为1;dim=1表示按行计算Softmax值,每一行上的和为1。使用Softmax必须显式给出dim,否则结果不确定。
在PyTorch中应用Softmax激活函数:
>>> input_data = autograd.Variable(torch.randn(2,3))
>>> print(input_data)
tensor([[-0.3776, 0.6697, 0.7186],
[-1.0892, 0.1614, 1.2264]])
>>> Softmax = nn.Softmax(dim=1)
>>> print(Softmax(input_data))
tensor([[0.1461, 0.4165, 0.4374],
[0.0684, 0.2388, 0.6928]])
7.LogSoftmax
在应用Softmax函数前,对输入应用对数函数,就是LogSoftmax,公式如下:
f ( x i ) = l o g e x p ( x i ) ∑ j e x p ( x j ) f(x_i)=log\frac{exp(x_i)}{\sum_{j}exp(x_j)} f(xi)=log∑jexp(xj)exp(xi)
PyTorch中的定义同样接受一个dim参数,含义和用法跟Softmax相同,这里不再赘述。
PyTorch中更多的预定义激活函数详见PyTorch的官方文档。
3.前向算法
当我们使用前馈神经网络接收输入 x x x,并产生输出 y ^ \hat y y^时,信息通过网络向前流动。输入 x x x提供初始信息,向输出的方向传播到每一层的神经元,并跟相应的权重做运算,最终产生输出 y ^ \hat y y^,这个过程称为前向传播(Forward Propagation)。
下面结合图示详细说明前向传播过程。
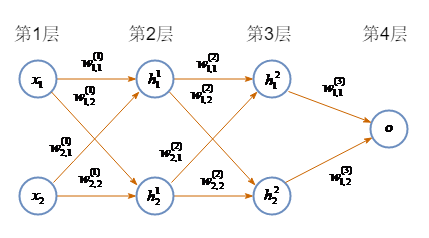
上图所示是一个只有4层的神经网络,其中第1层为输入层,第4层为输出层,第2层和第3层为隐含层。 x 1 x_1 x1和 x 2 x_2 x2是输入层中的两个神经元, h i k h_{i}^{k} hik表示第 k k k个隐含层中的第 i i i个神经元, w i , j ( l ) w_{i,j}^{(l)} wi,j(l)表示第 l l l层中第 i i i个神经元到第 l + 1 l+1 l+1层中第 j j j个神经元的权重,箭头表示信息传播方向,即输入层——>隐含层——>输出层。
前向传播过程中 h 1 1 h_{1}^{1} h11的值为所有输入到该神经元的信息和相应连接上权重的加权求和。公式为:
z h 1 1 = x 1 ∗ w 1 , 1 ( 1 ) + x 2 ∗ w 2 , 1 ( 1 ) + b 1 z_{h_{1}^{1}}=x_1 * w_{1,1}^{(1)} + x_2 * w_{2,1}^{(1)} + b_1 zh11=x1∗w1,1(1)+x2∗w2,1(1)+b1
z h 2 1 = x 1 ∗ w 1 , 2 ( 1 ) + x 2 ∗ w 2 , 2 ( 1 ) + b 2 z_{h_{2}^{1}}=x_1 * w_{1,2}^{(1)} + x_2 * w_{2,2}^{(1)} + b_2 zh21=x1∗w1,2(1)+x2∗w2,2(1)+b2
其中, b b b为偏置项。这样就得到了隐含层中神经元的多元输入信息 z h 1 1 z_{h_{1}^{1}} zh11和 z h 2 1 z_{h_{2}^{1}} zh21,随后将多元输入通过激活函数 f f f得到各个神经元的输出值 y h 1 1 y_{h_{1}^{1}} yh11和 y h 2 1 y_{h_{2}^{1}} yh21:
y h 1 1 = f ( z h 1 1 ) y_{h_{1}^{1}}=f(z_{h_{1}^{1}}) yh11=f(zh11)
y h 2 1 = f ( z h 2 1 ) y_{h_{2}^{1}}=f(z_{h_{2}^{1}}) yh21=f(zh21)
y h 1 1 y_{h_{1}^{1}} yh11为第1个隐含层中神经元 h 1 1 h_{1}^{1} h11的输出值,随着信息在网络中传播,它同时也是第2个隐含层的输入信息,例如此时 h 1 2 h_1^2 h12的输入信息为 y h 1 1 y_{h_{1}^{1}} yh11和 y h 2 1 y_{h_{2}^{1}} yh21。按照这个过程,直到得到最终输出层神经元的值 y o y_o yo,这就完成了一次完整的前向传播过程。
前向传播是预测的过程,对每一个训练集中的实例,通过神经网络计算每一层的输出,最终得到整个网络的输出,这个输出与真实值的差别可以评估当前参数集的好坏,然后从神经网络结果中的最后一个隐含层计算,每一层对整体的误差“贡献”了多少,这个过程就是反向传播了。前向算法通过网络中的每个层和激活函数最终产生输出。在训练过程中,前向传播可以持续向前,直到产生一个标量代价函数 J ( θ ) J(\theta) J(θ)。
前向传播算法描述如下:
Require:网络深度,1
Require: W ( i ) , i ∈ { 1 , . . . , l } W^{(i)},i \in { \{ 1,...,l \} } W(i),i∈{1,...,l},模型权重矩阵
Require: b ( i ) , i ∈ { 1 , . . . , l } b^{(i)},i \in { \{ 1,...,l \} } b(i),i∈{1,...,l},模型偏置参数
Require: x x x,程序的输入
Require: y y y,目标输出
h ( 0 ) = x h^{(0)}=x h(0)=x
for k = 1 , . . . , l k=1,...,l k=1,...,l do
a ( k ) = b ( k ) + W ( k ) h ( k − 1 ) a^{(k)}=b^{(k)}+W^{(k)}h^{(k-1)} a(k)=b(k)+W(k)h(k−1)
h ( k ) = f ( a ( k ) ) h^{(k)}=f(a^{(k)}) h(k)=f(a(k))
End for
y ^ = h ( l ) \hat y=h^{(l)} y^=h(l)
J ( θ ) = L ( y ^ , y ) + λ Ω ( θ ) J(\theta)=L(\hat y, y) + \lambda \Omega(\theta) J(θ)=L(y^,y)+λΩ(θ)
4.损失函数
本小节我们来介绍损失函数。首先介绍损失函数的概念,然后介绍损失函数在回归问题和分类问题上的应用,最后介绍PyTorch中常用的一些损失函数。
1.损失函数的概念
损失函数(Loss Function)又称为代价函数或成本函数(Cost Function),是一个非负的实数函数,通常用 L L L表示。损失函数用来量化在训练过程中,网络输出和真实目标间的差距。损失函数是神经网络中特殊的层。在前向算法中,每个输入信息在网络中流动,最终到达输出层,产生预测值 y ^ \hat y y^。然后对数据集中所有的预测误差求平均,这个平均误差反映神经网络的好坏情况。确定神经网络最佳状态相当于寻找使损失最小的神经网络参数。这样一来,损失函数的出现使网络的训练变成一个优化问题。神经网络的参数很多,在大多数情况下很难通过分析来确定,但是可以利用优化算法近似地求解,例如利用梯度下降方法求解最值。
这里需要强调的一点是,损失函数的值仅跟网络中权重 w w w和偏置 b b b有关。在给定的神经网络中特定的数据集下,网络的损失完全依赖于网络的状态,也就是参数 w w w和 b b b。 w w w和 b b b的变化会导致网络的输出变化,从而影响网络的损失。所以前向过程中方程可以写成 h ( x ) w , b = y ^ h(x)_{w,b}=\hat y h(x)w,b=y^,即在 w w w和 b b b条件下对于输入 x x x网络的输出是 y ^ \hat y y^。
在一定程度上可以说损失函数越小,模型越好。为什么这么说呢?因为 L L L的均值称为经验风险函数,但是并不是经验风险函数越小越好,比如模型复杂度过高会产生过拟合现象,这个时候经验风险是很小的,可过拟合的模型并不是我们想要的结果。这里需要引入另外一个概念:正则化。正则化也叫结构风险,用来表示模型的复杂度。我们把经验风险和结构风险的和称为目标函数。神经网络训练的最终目标就是寻找最佳的参数,使目标函数最下。后面我们会对正则化展开详细的讨论。
下面介绍一下常用的损失函数。损失函数根据用途通常可以分成两类:一类是用于回归问题,另一类是用于分类问题。
2.回归问题
在回归问题中常用的损失函数是均方差(Mean Squared Error,MSE)损失,回归中的输出是一个实数值,这里采用的平方损失函数类似于线性回归中的最小二乘法。对于每个输入实例都只有一个输出值,把所有输入实例预测值和真实值间的误差求平方,然后求平均,公式如下:
L ( W , b ) = 1 2 N ∑ i = 1 N ( y ^ i − y i ) 2 L(W,b)=\frac{1}{2N}\sum_{i=1}^{N}(\hat y_i-y_i)^2 L(W,b)=2N1i=1∑N(y^i−yi)2
其中, y ^ i \hat y_i y^i是第 i i i个输入的预测值, y i y_i yi是第 i i i个输入的真实值, N N N为输入集中的个数。对于多输入的个数,MSE公式为:
L ( W , b ) = 1 2 N M ∑ i = 1 N ∑ j = 1 M ( y ^ i j − y i j ) 2 L(W,b)=\frac{1}{2NM}\sum_{i=1}^{N}\sum_{j=1}^{M}(\hat y_{ij}-y_{ij})^2 L(W,b)=2NM1i=1∑Nj=1∑M(y^ij−yij)2
其中, j j j表示输出中的第 j j j个值,大多时候会在前面乘以1/2,这样可以与平方项求导得出来的2约掉,方便后续计算。
MSE在回归中应用很广泛,但是它对异常值很敏感,在特定的任务中有时不需要考虑异常值(比如股票的选择中需要考虑异常值,但是在买房的时候就不需要过多考虑),这时就需要损失函数更关注中位数而不是平均数。这时可以选择平均绝对误差(Mean Absolute Error,MAE),公式如下:
L ( W , b ) = 1 N M ∑ i = 1 N ∑ j = 1 M ∣ y ^ i j − y i j ∣ L(W,b)=\frac{1}{NM}\sum_{i=1}^{N}\sum_{j=1}^{M}|\hat y_{ij}-y_{ij}| L(W,b)=NM1i=1∑Nj=1∑M∣y^ij−yij∣
MAE为数据集上所有误差绝对值的平均数。
3.分类问题
神经网络可以解决分类问题,即判断输入属于哪个类别,例如一张图片是猫还是狗,收到的邮件是否是垃圾邮件等。还有一种分类问题,我们的神经网络模型预测值往往不是特定的类别,而是属于某一个类别的概率,比如前面提到的垃圾邮件问题,神经网络的输出结果为20%可能是垃圾邮件,80%可能不是垃圾邮件。接下来介绍一下分类问题中常用的损失函数。
对于0-1分类问题,可以使用铰链损失(Hinge Loss),1表示属于某一类别,0表示不属于该类别。大多用-1和1代替0和1,这时铰链损失的公式如下:
L ( W , b ) = 1 N ∑ i = 1 N m a x ( 0 , 1 − y i × y ^ ) L(W,b)=\frac{1}{N}\sum_{i=1}^{N}max(0,1-y_i \times \hat y) L(W,b)=N1i=1∑Nmax(0,1−yi×y^)
Hinge Loss只可以解决二分类问题,对于多分类问题,可以把问题转化为二分类来解决:对于N分类任务,每次只考虑是否属于某一特定的类别,把问题转化成N个二分类问题。
对于前面提到的预测属于某一类别的概率的问题,可以使用负对数似然损失函数(Negative Log Likelihood Loss Function)。接下来举例说明一下负对数似然函数。为了叙述方便,这里同样使用二分类问题为例,区别是这里的二分类问题不是硬分类问题,而是要预测属于某一类别的概率,用 h ( x i ) h(x_i) h(xi)和 1 − h ( x i ) 1-h(x_i) 1−h(xi)表示给定输入 x i x_i xi的输出,即属于某一类别的概率,用 W W W和 b b b表示网络权重和偏置,公式为:
P ( y i = 1 ∣ x i ; W , b ) = h W , b ( x i ) P(y_i=1|x_i;W,b)=h_{W,b}(x_i) P(yi=1∣xi;W,b)=hW,b(xi)
P ( y i = 0 ∣ x i ; W , b ) = 1 − h W , b ( x i ) P(y_i=0|x_i;W,b)=1-h_{W,b}(x_i) P(yi=0∣xi;W,b)=1−hW,b(xi)
上面两个式子可以整合在一起:
P ( y i ∣ x i ; W , b ) = ( h W , b ( x i ) ) y i × ( 1 − h W , b ( x i ) ) 1 − y i P(yi|x_i;W,b)=(h_{W,b}(x_i))^{y_i} \times (1-h_{W,b}(x_i))^{1-y_i} P(yi∣xi;W,b)=(hW,b(xi))yi×(1−hW,b(xi))1−yi
所以损失函数可以写成:
L ( W , b ) = ∏ i = 1 N y ^ y i × ( 1 − y ^ i ) 1 − y i L(W,b)=\prod_{i=1}^{N}{\hat y}^{y_i} \times (1-\hat y_i)^{1-y_i} L(W,b)=i=1∏Ny^yi×(1−y^i)1−yi
为了计算方便,利用对数函数把乘积的形式变成求和,因为对数函数是单调的,取对数函数的最大化和取负对数函数的最小化是等价的,就得出了负对数似然损失函数的公式:
L ( W , b ) = − ∑ i = 1 N ( y i × l o g y ^ i + ( 1 − y i ) × l o g ( 1 − y ^ i ) ) L(W,b)=-\sum_{i=1}^{N}(y_i \times log{\hat y_i} + (1-y_i) \times log{(1-\hat y_i)}) L(W,b)=−i=1∑N(yi×logy^i+(1−yi)×log(1−y^i))
我们把问题从二分类扩展到多分类上,用one-hot编码表示类别的预测结果:属于该类别的为1,其他的全为0,公式如下:
L ( W , b ) = − ∑ i = 1 N ∑ j = 1 M y i , j × l o g y ^ i L(W,b)=-\sum_{i=1}^{N}\sum_{j=1}^{M}y_{i,j} \times log{\hat y_i} L(W,b)=−i=1∑Nj=1∑Myi,j×logy^i
从形式上看这个函数恰好是交叉熵的形式,因此负对数似然损失函数又叫做交叉熵损失函数(Cross Entropy Loss Function)。交叉熵是不确定性信息的一种度量,在这里交叉熵用来衡量我们学习到的 y ^ \hat y y^和真实目标值 y y y的不确定性。对于所有的输入 x x x,如果每个结果越接近目标值,也就是 h a t y hat y haty和 y y y的误差越小,则交叉熵越小;反之,输出结果距离目标值越远,则交叉熵越大。
4.PyTorch中常用的损失函数
前面从损失函数的理论层面做了一些简单介绍,在PyTorch中已经对常用的损失函数做好了封装,在系统中直接调用相应的损失函数即可。接下来介绍常用的损失函数在PyTorch中的实现。
(1)MSELoss
PyTorch中MSELoss的定义:
class torch.nn.MSELoss(size_average=True, reduce=True)
参数含义:
- size_average:True表示此时的损失是每个minibatch的平均;False表示此时的损失是对每个minibatch的求和,默认为True。这个属性只有当reduce为True时才生效。
- reduce:默认为True,此时损失会根据size_average参数的值计算每个minibatch的平均或者求和;如果设置为False,则忽略size_average参数的值,直接返回每个元素的损失。
使用方法举例:
>>> loss = nn.MSELoss()
>>> input = autograd.Variable(torch.randn(3,5),requires_grad=True)
>>> target = sutograd.Variable(torch.randn(3,5))
>>> output = loss(input,target)
>>> output.backward()
(2)L1Loss
L1Loss即前面提到的MAE,在PyTorch中的定义为:
class torch.nn.L1Loss(size_average=True, reduce=True)
参数含义和MSE的一样。
(3)BCELoss
BCELoss用在二分类问题中,PyTorch中的定义为:
class torch.nn.BCELoss(weight=None, size_average=True)
参数含义:
-weight:指定batch中每个元素的Loss权重,必须是一个长度和batch相等的Tensor
-size_average:True表示此时的损失是每个minibatch的平均;False表示此时的损失是对每个minibatch的求和,默认为True。
在使用BCELoss时,需要注意的是,每个目标值( y ^ i \hat y_i y^i)都要求在(0,1)之间,可以在网络最后一层使用Sigmoid函数达到这个要求。
示例:
>>> m = nn.Sigmoid()
>>> loss = nn.BCELoss()
>>> input = autograd.Variable(torch.randn(3), requires_grad=True)
>>> target = autograd.Variable(torch.FloatTensor(3).random_(2))
>>> output = loss(m(input), target) # 前向输出时使用Sigmoid函数
>>> output.backward()
(4)BCEWithLogitsLoss
BCEWithLogitsLoss在PyTorch中的定义为:
class torch.nn.BCEWithLogitsLoss(weight=None,size_average=True)
BCEWithLogitsLoss同样使用在二分类任务中,参数含义和BCELoss相同。与BCELoss不同的是,它把Sigmoid函数集成到函数中,在实际应用中比Sigmoid层加BCELoss层再数值上更加稳定,因为把两个层合并时可以使用LogSumExp的优势来保证数值的稳定性。
(5)NLLLoss
NLLLoss使用在多分类任务中的负对数似然损失函数,我们用C表示多分类任务中类别的个数,用N表示minibatch,则NLLLoss的输入必须是(N,C)的二维Tensor,即数据集中每个实例对应每个类别的对数概率,可以在网络最后一层应用LogSoftmax层来实现。PyTorch中NLLLoss的定义为:
class torch.nn.NLLLoss(weight=None,size_average=True,ignore_index=-100,reduce=True)
参数含义:
- size_average和reduce,和前面介绍的一样。
- weight:可以指定一个一维的Tensor,用来设置每个类别的权重。若用C来表示类别的个数,则Tensor的长度就是C。当训练集不平衡时该参数十分有用。
-ignore_index:可以设置一个被忽略值,使这个值不会影响到输入的梯度计算。当size_average为True时,loss的平均值也会忽略该值。
这里要特别说明一点:输出根据reduce而定,如果reduce为True则输出为一个标量,如果reduce为False则输出为一个长度为N的Tensor。
(6)CrossEntropyLoss
CrossEntropyLoss同样是多分类任务的交叉熵损失函数,前面提到,在NLLLoss的输出层要应用一个LogSoftmax函数,CrossEntropyLoss就是LogSoftmax和NLLLoss的组合。可以使用NLLLoss的任务都可以使用CrossEntropyLoss,而且更简洁,PyTorch中的定义为:
class torch.nn.CrossEntropyLoss(weight=None,size_average=True,ignore_index=-100,reduce=True)
参数含义和NLLLoss完全相同。
以上几种损失函数是PyTorch中最常用的几种,更多损失函数可以参考PyTorch官网损失函数模块。
5.反向传播算法
前向算法中,需要W参与运算,W是网络中各个连接上的权重,这个值需要在训练过程中确定,在传统的机器学习方法(如逻辑回归)中,可以通过梯度下降来确定权重的调整。逻辑回归可以看做是没有隐含层的神经网络,但是在多元感知机中如何获取隐含层的权重是很困难的,我们能做的是计算输出层的误差更新参数,但在隐含层误差是不存在的。虽然无法直接获取隐含层的权重,但是我们知道在权重变化后输出误差的变化,那么能否通过实际输出值和期望输出值间的差异来间接调整权重呢?预测值和真实值之间的差别可以评估输出层的误差,然后根据输出层的误差,计算在最后一个隐含层中的每个神经元对输出层误差影响了多少,最后一层隐含层的误差又由其前一层隐含层计算得出。如此类推,直到输入层。这就是反向传播(BackPropagation,BP)算法的基本思想。
反向传播算法是1986年由Rumelhart和McCelland为首的科研小组提出的。反向传播基于梯度下降策略,是链式求导法则的一个应用,以目标的负梯度方向对参数进行调整。这是一场以误差(Error)为主导的反向传播运动,旨在得到最优的全局参数矩阵,进而将多层神经网络应用到分类或者回归任务中去。
反向传播算法的原理及详细推导过程请参考博客《反向传播算法(过程及公式推导)》。感谢原创,作者是个大牛!
在具体的应用中,成熟的深度学习工具包都完成了对这些操作的封装。PyTorch封装了这一系列复杂的计算,前面提到过PyTorch中所有的神经网络的核心是autograd自动求导包。这里结合反向传播进行说明。
torch.autograd包的核心是Variable类,它封装了Tensor支持的所有操作,在程序中一旦完成了前向的运算,就可以直接调用.backward()方法,这时候所有的梯度计算会自动进行。如果Variable是标量的形式(只有一个元素),你不必指定任何参数给backward()函数。不过,如果它有更多的元素,就需要去指定一个和Variable形状匹配的grad_variables参数,用来保存相关Variable的梯度。
PyTorch中海油一个针对自动求导的实现类:Function。Variable和Function是相互联系的,并且它们构建了一个非循环的图,编码了一个完整的计算历史信息。每一个Variable都有一个.grad_fn属性,引用一个已经创建的Function。
PyTorch中反向传播的例子:
import torch
from torch.autograd import Variable
x = Variable(torch.ones(2,2),requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
out.backward()
6.数据处理类
我们要使用的数据需要转换成PyTorch能够处理的格式。PyTorch中提供了torch.utils.data.Dataset类对数据进行封装,是所有要加载的数据集的父类。在定义Dataset的子类时,需要重载两个函数:len_和_getitem。其中,_len_返回数据集的大小;_getitem_实现数据集的下标索引。
在创建DataLoader时会判断_getitem_返回值的数据类型,然后用不同的分支把数据转换成相应的张量。因此,_getitem_返回值的数据类型可选择范围很多。比如图像可以选择numpy.array类型,标记可以选择int类型。
现在有了由数据文件生成的结构数据,那么怎么在训练时提供batch数据呢?PyTorch提供了生成batch数据的类。PyTorch用类torch.utils.data.DataLoader加载数据,并对数据进行采样,生成batch迭代器。
class torch.utils.data.DataLoader(dataset, batch_size=1, shuffle=False, sampler=None, batch_sampler=None, num_workers=0, collate_fn=, pin_memory=False, drop_last=False)
参数含义:
- dataset:Dataset类型,指定要加载的数据
- batch_size:指定每个batch加载多少个样本,默认为1
- shuffle:指定是否在每个epoch中对数据进行打乱
- sampler:从数据集中采样的策略
-batch_sampler:批量采样策略,一次返回一批指标
-num_works:加载数据时使用多少子进程。默认值为0,表示只在主进程中加载数据
-collate_fn:定义函数来合并样本以形成一个mini-batch- pin_memory:如果为True,此时数据加载器会将张量复制到CUDA固定内存中,然后返回它们
-drop_last:如果为True,最后一个不完整的batch将被丢弃
7.示例:单层神经网络实现
本节使用神经网络在iris数据集的多分类示例来说明神经网络的整个流程。一般的神经网络训练包括几个重要的步骤:数据准备,初始化权重,激活函数,前向计算,损失函数,计算损失,反向传播,更新参数,直到收敛或者达到终止条件。
import torch
from torch import sigmoid
import torch.nn.functional as F
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from torch.autograd import Variable
from torch.optim import SGD
N_FEATURE = 4
N_HIDDEN = 5
N_OUTPUT = 4
N_ITERS = 1000
LR = 0.5
# 判断GPU是否可用
use_cuda = torch.cuda.is_available()
print("use_cuda: ",use_cuda)
# 加载数据集
iris = load_iris()
print(iris.keys())
# 数据预处理
x = iris['data']
y = iris['target']
print('x.shape: ',x.shape)
print('y.shape: ',y.shape)
print(y)
x = torch.FloatTensor(x)
y = torch.LongTensor(y)
x = Variable(x)
y = Variable(y)
# 定义神经网络类,继承自torch.nn.Module
class Net(torch.nn.Module):
# 定义构造函数
def __init__(self,n_feature, n_hidden, n_output):
super(Net,self).__init__()
# 定义隐含层
self.hidden = torch.nn.Linear(n_feature,n_hidden)
# 定义输出层
self.predict = torch.nn.Linear(n_hidden,n_output)
# 定义前向传播
def forward(self,x):
# 计算隐含层,激活函数为sigmoid
x = sigmoid(self.hidden(x))
# 计算输出层,激活函数为log_softmax(多分类)
out = F.log_softmax(self.predict(x),dim=1)
return out
# 定义神经网络实例
net = Net(n_feature=N_FEATURE,n_hidden=N_HIDDEN,n_output=N_OUTPUT)
print(net)
# 如果GPU可用,把数据和模型都转到GPU上计算;CPU时调用.cpu()即可
if use_cuda:
x = x.cuda()
y = y.cuda()
net = net.cuda()
# 定义神经网络优化器:这里使用随机梯度下降SGD,学习率lr=0.5
optimizer = SGD(net.parameters(),lr=LR)
# 开始训练神经网络
px,py = [],[]
for i in range(N_ITERS):
# 数据集传入网络前向计算预测值
prediction = net(x)
# 计算损失
loss = F.nll_loss(prediction,y)
# 清除网络状态
optimizer.zero_grad()
# 误差反向传播
loss.backward()
# 更新参数
optimizer.step()
# 打印并记录当前的index和loss
print(i," loss: ",loss.item())
px.append(i)
py.append(loss.item())
plt.figure(figsize=(6,4),dpi=144)
plt.plot(px,py,'r-',lw=1)
plt.yticks([x * 0.1 for x in range(16)])
plt.show()
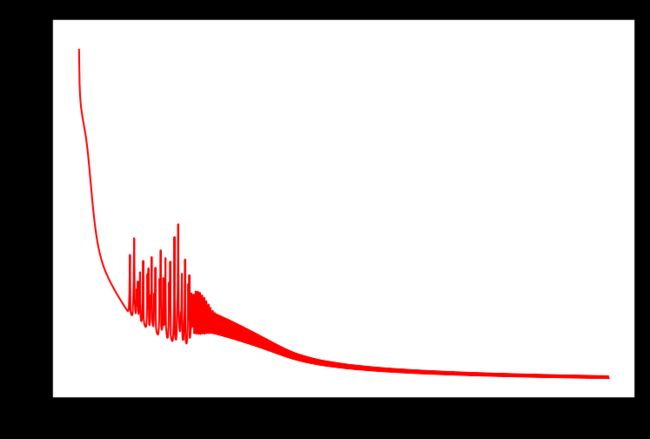
代码输出如下:
use_cuda: True
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
x.shape: (150, 4)
y.shape: (150,)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Net(
(hidden): Linear(in_features=4, out_features=5, bias=True)
(predict): Linear(in_features=5, out_features=4, bias=True)
)
0 loss: 1.3780320882797241
1 loss: 1.244009017944336
2 loss: 1.1953575611114502
3 loss: 1.1671373844146729
4 loss: 1.147063136100769
5 loss: 1.1312648057937622
6 loss: 1.1179096698760986
7 loss: 1.10591721534729
8 loss: 1.0945632457733154
9 loss: 1.0833168029785156
10 loss: 1.0717663764953613
……
990 loss: 0.08581560850143433
991 loss: 0.0774485245347023
992 loss: 0.08574181795120239
993 loss: 0.07738661766052246
994 loss: 0.08566807955503464
995 loss: 0.07732491940259933
996 loss: 0.08559456467628479
997 loss: 0.07726352661848068
998 loss: 0.08552153408527374
999 loss: 0.0772024393081665
训练过程中损失的变化如下图所示: