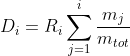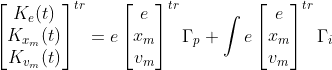空间机器人在轨任务的制导、导航与控制:综述与展望
空间机器人在轨任务的制导、导航与控制:综述与展望
On the guidance, navigation and control of in-orbit space robotic missions: A survey and prospective vision
作者:Borna Monazzah Moghaddam, Robin Chhabra
Acta Astronautica (2021)
摘要:
在第一部分,本文概述了用于执行在轨机器人任务的空间操纵器的制导、导航和控制(GNC)方法,包括但不限于在轨服务(on-orbit sevicving)、卫星\卫星站组装(satellite/station assembly)、探测外星物体(probing extra-terrestrial objects)和空间碎片减缓(space debris mitigation)。本文简要介绍了一些空间任务的概念,讨论了空间机器人是最实用和通用的解决方案之一。一个在轨机器人任务的共同阶段被确定为:近距离交会(close-range rendezvous),姿态同步(attitude synchronization),目标识别(target identification),机械手部署(manipulator deployment),捕获(capture),如果需要,捕获后机动(post-capture maneuvers)。对每个阶段提出或适用的重要GNC方法进行了广泛的审查。本文重点研究了用于姿态同步、机械臂部署和捕获阶段的GNC方法,特别是用于自由漂浮(free-floating)和自由飞行(free-flying)两种工作状态的GNC方法。空间机械臂系统的运动学和动力学是为了帮助统一不同GNC方法背后的主要思想。使用本文提供的统一符号、比较表和讨论,研究人员可以比较各种GNC方法,并为下一代空间机器人GNC系统做出贡献。此外,这项调查还帮助技术用户了解在轨机器人任务,并为特定应用选择合适的GNC技术。本文的第二部分介绍了两种新兴的基于强化学习和几何力学的控制方案,它们是空间机器人系统GNC中有前途的研究方向。讨论了实现这些技术对在轨机器人任务GNC的好处。一项关于影响空间机械臂的环境扰动及其对长期自主的威胁的独家研究总结了这篇文章。
1.简介
最近主要的国际太空探索计划旨在回答有关人类的基本问题,例如:“地球以外是否有生命?”,“在太阳系中,能源和材料的替代来源是什么?”,“宇宙对人类生存的威胁是什么?”。这些项目主要集中在通过载人或机器人任务访问我们最近的天体邻居,即月球和火星。阿波罗计划中的载人登月任务被认为是航天工业历史上的一个转折点。月球地球物理研究是通过在其轨道上放置ARTEMIS和月球侦察轨道器,或在其表面放置月球车和玉兔来进行的。苏联第一个登陆器发送到火星表面(火星2、3和6),其次是许多成功的国家航空和宇宙航行局(NASA)在火星探索计划,例如,火星机器包括Spirit号、Opportunity号、Sojourno号、Curiosity号、和 landers号包括Viking号和Pathfinder号,寻找生命迹象,并为未来的载人任务检查火星环境。除了探索太空,人类也用星座卫星在地球轨道以促进电信和地理空间定位(GPS、Glonass和BaiDou),或从一个完美的角度来研究地球(哥白尼、铱卫星),观察宇宙(詹姆斯·韦伯和开普勒望远镜),并证明和测试我们进一步探索太阳系的能力。在我们最令人印象深刻的合作成就中,包括美国宇航局、俄罗斯航天局(ROSCOSMOS)、欧洲航天局(ESA)、日本宇宙航空研究开发机构(JAXA)和澳大利亚航天局在内的许多国家和公司都为建设国际空间站(ISS)作出了贡献。最初的目标是研究微重力和外层空间环境对人体和人造技术的影响。在更雄心勃勃的尝试中,Cassini号被送往土星及其卫星,以揭开它们的地球物理和大气的奥秘。欧洲航天局的“Rosetta”任务能够通过复杂的行星轨道机动拦截一颗小行星并在其上着陆。最后,Voyager1号和2号宇宙飞船已经到达了我们太阳系的边缘,这是迄今为止任何人造物体所到达的最远距离。
先进的机器人技术是任何可持续空间探索和开发计划的组成部分。空间机器人系统不仅是完成空间任务的关键使能技术,而且也是维持现有空间基础设施以确保卫星系统(如电信、地球\宇宙观测、全球导航系统、军事监视、天气预报、等等),并在低地球轨道之外建造新的卫星。空间机器人的作用特别重要,因为它们在敌对的和部分已知的外层空间环境中不知疲倦地和具有成本效益地工作,而不危及人类生命。
与轨道飞行器和深空飞行器建立遥测连接是一个主要问题。由于不可避免的通信延迟,不可能总是从地面站实时遥控它们。另一方面,让人类操作员长时间停留在轨道上或远离地球表面,在逻辑上、经济上、有时在道德上都是不可行的。因此,空间任务(特别是涉及处理地球或其他行星轨道上的物体的任务)极大地受益于弹性和智能自主机器人系统,它们有能力做出局部决策。这推动了用于太空探索和开发的自主机器人系统的蓬勃发展,其中最突出的是空间机械臂[1]。在20世纪80年代,一些研究人员和组织开始研究在航天器上为轨道服务任务整合机器人操纵器的想法[2,3]。对遥操作机器人在太空中的可能应用进行了研究。1986年,美国国家航空航天局(NASA)开发了一种机器人概念,用于将空间站的轨道替换单元转移到其附近[5]的轨道服务车。
空间机器人的一个直接用途是通过卫星在轨服务(OOS)来维护空间资产。各机构开始对卫星进行补充燃料(re-fuel)、维修(repair)、服务(service)(部分更换)、重新入轨(re-orbit)或退役(retire)的方法,特别是在地球同步赤道轨道(GEO)系统中,因为该系统拥有大量卫星。空间领域参与者的另一个主要担忧是,让停用的卫星不受控制地留在地球轨道上可能产生的破坏性影响。太空碎片会造成级联碰撞灾难,威胁航天器和卫星的安全。这种灾难以唐纳德·j·凯斯勒(Donald J. Kessler)的名字命名,他在1978年首次警告了这一现象。世界各地的研究人员开始提出合适的方法来捕捉、操纵或处理这些轨道物体。其中一种减缓方法是用网捕捉碎片或用绳索拖拽碎片。其中发展的方法是使用单根或分支系链[8],动量交换束缚绳[9],缆索牵引绳[10 12],粘弹性绳[13]和电动绳[14]。离子束将碎片推出轨道[15]、通过鱼叉捕获碎片[16,17]、抓钩系统[18]和拖动增强装置[19]是其他碎片减缓方法的例子。与此同时,其他研究人员也在致力于为在轨卫星提供服务、加油和维修,以使旧卫星继续运行。一个服务解决方案需要与目标卫星对接,该任务首先在日本的机器人卫星ETS-VII[20](工程测试卫星VII如图1[21]所示)上进行了试验。
最近人们对观测、研究、采样甚至采矿小行星的兴趣的增长,也为研究人员提出自主机器人系统以实现空间资本化提供了机会。在Hayabusa号和Hayabusa-2号任务中,日本航天局在微重力环境下成功地使用了机器人小行星采样器[22 25]。源光谱释义资源安全风化层辨认探测器(OSIRIS-REx,图2)是美国宇航局的一个机器人任务,通过机器人手臂[26],以连续起飞(TAG)轨道前往近地小行星Bennu,收集样本。近地小行星回收任务(ARM)结合了机器人和人类探索来捕获深空的非合作小行星并将其带回地球[27]。非合作目标,而不是合作目标,是一个空间物体,不是主动控制,以方便机器人航天器对接和操纵。小行星也可能对地球上的生命构成威胁。利用自主解决方案对具有潜在破坏性的小行星进行在轨操纵或偏转的行星防御机制,已成为空间机器人领域研究人员的另一个主要担忧。这些方法包括:离子束使小行星[15]偏离轨道,一个巨大的引力牵引器(利用相互引力来操纵小行星的轨道)[28],通过镜子[29]、太阳光羽[30]和控制与物体[31]的碰撞来偏离轨道。
在减少碎片(mitigate debris)、使小行星偏转(deflect asteriods)、采集小行星样本(sample asteroids)、修复或给在轨系统加燃料(repair or refuel on-orbit system)等方面,最显著的建议之一是使用自主空间操纵器系统。这些系统目前通过远程操作用于对接和处理有效载荷[32,33]。关于地面和空间机械臂系统有大量的背景知识(如图3所示的国际空间站[34]上的Canadarm2)。与其他方法不同的是,空间机械臂提供对目标行为的可预测控制,更重要的是,它们被认为是执行各种空间任务的通用解决方案。空间机械臂系统由安装在航天器上的机械臂组成。该基地航天器拥有卫星的所有组件,如推进器、姿态确定和控制系统(ADCS)、电子、遥测和其他子系统。它的有效载荷,即机械臂,将一直收回,直到卫星进入轨道并在后期部署为止。在轨空间机器人任务分为6个阶段:(i) 机动中的近距离会合和近距离接近;(ii) 目标识别;(iii) 必要时与目标的姿态同步;(iv) 机械臂部署;(v) 捕获; (vi) 捕获后机动。
卫星、仪器或整个空间站的在轨组装和维护是空间操纵器的另一个应用领域。其中最著名的是Candarm2(也被称为空间站遥控操纵系统或简称SSRMS),它是由加拿大航天局(CSA)和Macdonald Dettwiler and Associates (MDA)(遥感通信公司)开发的,用来帮助捕获来的船员舱和有效载荷,组装国际空间站,协助航天员进行舱外活动(EVA)[34],如图3所示。Canadarm2是Canadarm1(也称为航天飞机遥控操纵系统或简称SRMS)的继任者,在航天飞机上操作,以促进其与有效载荷和国际空间站的对接、部署和交互。一个不太为人所知的(但绝非低影响)是Dextre(也被称为特殊目的灵巧操作器或简称SPDM),一个与Canadarm2一起的两臂远程操作机器人,是国际空间站[35]上的移动服务系统(MBS)的一部分。Dextre是另一个加拿大制造的机器人,用于国际空间站的修复操作,否则需要宇航员的EVA[36]。空间机械臂应用的自然进展将是在深空探测任务中部署它们,用于组装和维护未来近地轨道以外的空间站。加拿大的下一代空间机械臂将被送往月球轨道,以协助探索和建立一个永久的月球门户,与美国宇航局合作。一个艺术家描绘的这个机械手的早期设计,设想由CSA提出,是在图4可视化。
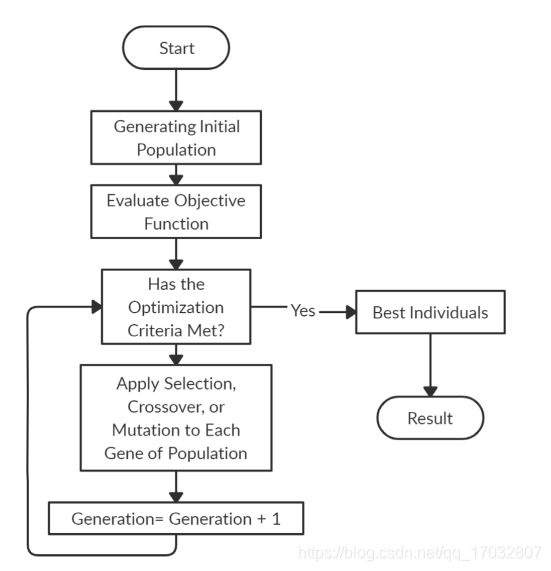
本文综述了航天器机械臂系统在轨机器人任务各个阶段的制导、导航和控制(GNC)方法。机器人系统通过三个主要步骤来规划和执行任务:(i) 估计它们的当前状态和它们的环境交互作用(导航);(ii) 根据任务要求和系统当前状态(制导)生成一组期望状态;(iii) 计算\施加控制输入给系统以遵循期望状态(控制)[37]。GNC方法以一种统一的方式提出,以提供一个系统的比较基础,并列出它们的功能和缺点。这使得研究人员和技术用户能够对在轨机器人任务的不同阶段进行GNC方法的比较和选择。第2节解释了任务、它们之间的相互作用以及每个阶段提议的GNC方法。第3节基于旋量理论和多体系统的欧拉拉格朗日方程,对耦合航天器机械臂系统的运动学和动力学进行了简单的表述。开发的表示法将在整个论文中使用,以呈现GNC方法背后的主要思想。在第4节中,讨论了在手臂展开之前采用的同步技术及其各自的优缺点。在自由浮动或自由飞行操作制度的手臂控制GNC方法在第5节中进行了彻底的研究。最优,自适应,鲁棒,变分和案例特定的控制器报告,制定和解释在这一节。第6节解释了捕获阶段和捕获后机动的GNC方法。第7节介绍了两种可以显著改善航天器操纵系统GNC的新方法,即强化学习和几何力学。最后,在第8节中讨论了轨道环境中的干扰及其在GNC设计中的意义。图5显示了本文的信息流。本流程图说明了在轨机器人任务的上述各个阶段,并对每个阶段的操作模式进行了分解,并对不同模式下常用和专用的GNC方法进行了分类。在图表的右边列出了两个被调查的GNC技术家族的潜在贡献。
2、在轨机器人任务阶段
一种安装在航天器上的在轨道环境中运动的机器人机械臂(以下也称空间机械臂(space manipulator)、航天器机械臂(spacecraft-manipulator)或追逐机械臂系统(chaser-manipulator system))是一种在不同空间物体附近执行空间任务的引人注目的通用解决方案。在开始执行任务之前,空间机械臂位于一个停车轨道或一个空间站。它必须进行轨道机动,以移动到目标轨道,并与目标进行远距离交会。在这个尺度下,会合意味着到达距离目标[38]几公里的地方。
2.1 近距离交会机动
在机械手开始任何操作,如捕获(capturing)、靠泊(berthing)、修理(repairing)、升级(upgrading)、装配(assembling)等之前,跟踪航天器必须到达目标附近,进行交会,并与目标[39]同步其轨道运动。假设对接装置同时考虑了平移和旋转的相对运动,设计了跟踪器与合作或非合作目标对接的轨迹。Wei等人利用鲁棒滑模控制研究了追击器与非合作目标交会时的姿态和位置耦合控制问题。使用非线性模型预测控制[41]在两个阶段计划与一个翻滚的目标对接:(i) 在接近目标时,用进入锥调整追猎器;(ii) 在进入锥体内执行精确对接操作。算法基于Glidescope方法也提出了自主交会对接轨道目标Nolet和Miller通过对ISS[42]上SHPERES微卫星的多种GNC算法进行集成和测试,以估计另一个目标的状态,规划路径和控制跟踪运动[43]。与未控制卫星交会的最优路径规划算法构成了另一类已被深入研究的控制方案。Boyarko的方法是一个例子,解决了最小时间和最小能量集合问题的追逐者与一个翻滚的目标,以实现零相对位置和速度[45]。
2.1.1 对接目标
在不同的环境中,如行星旅行(planetary travel)、轨道站保持(orbital stationkeeping)和在较小天体上着陆(landing on smaller celestial bodies)等,轨道交会的基本技术有着丰富的背景。最著名的对接操作是由美国和俄罗斯为国际空间站和和平号等轨道空间站设计的空间项目。在他们的方法中,俄罗斯自动化了对接过程,这现在被认为是轨道机器人任务[46]的必要条件。这个问题已经通过不同的方法解决,从使用一个简单的闭环PID控制器或基于模型(Clohessy Wiltshire along Euler equation)制导和控制律[21]到应用更先进的自适应,最优或鲁棒控制方案。在这个问题中表达相对线性动力学的主要形式是通过Clohessy Wiltshire方程,这是一个圆形轨道上的相对线性运动在一阶近似的简化:
其中,
,
方程在目标坐标系中表示,![]() 是相对线性位置对目标,
是相对线性位置对目标,![]() 是两个的相对速度,n是平均轨道角速度,
是两个的相对速度,n是平均轨道角速度,![]() 是交会的持续时间,
是交会的持续时间,![]() 为灵敏度矩阵,下标0表示初始条件。相对姿态动力学的主要表示形式是欧拉方程:
为灵敏度矩阵,下标0表示初始条件。相对姿态动力学的主要表示形式是欧拉方程:
这里,![]() 是追逐者和目标在其身体坐标系中的惯性矩阵,
是追逐者和目标在其身体坐标系中的惯性矩阵,![]() 是同一坐标系下追逐者和目标的身体角速度,
是同一坐标系下追逐者和目标的身体角速度,![]() 是控制转矩并且
是控制转矩并且![]() 是机体坐标系的外部扰动。Xing和Parvez[47]提出了另一种确定追击者和目标在追击者坐标系中的相对动力学的方法:
是机体坐标系的外部扰动。Xing和Parvez[47]提出了另一种确定追击者和目标在追击者坐标系中的相对动力学的方法:
其中
![]() ,
,![]() 。
。
相对角速度形式为:
![]()
参数在它们各自的身体坐标系中表示。矩阵![]() 目标和追逐者坐标系之间的相对旋转(上标tr表示一个矩阵的转置)。同样,
目标和追逐者坐标系之间的相对旋转(上标tr表示一个矩阵的转置)。同样,![]() 是在追踪坐标系中表示的施加于追踪飞行器的总外力。
是在追踪坐标系中表示的施加于追踪飞行器的总外力。
优化方法可以与这些方程[48]结合使用,例如一般Bolza型成本函数[49]的形式![]() 并以速度限制的形式对成本参数[49]进行了现实约束
并以速度限制的形式对成本参数[49]进行了现实约束![]() 并且命令扭矩
并且命令扭矩![]() 。这里
。这里![]() 是成本函数加权参数,
是成本函数加权参数,![]() 是作动的长度和
是作动的长度和![]() 是追逐者的线速度。
是追逐者的线速度。
2.1.2 接近安全距离
各种在轨机器人任务包括追击机动,在一个安全距离与目标交会而不对接。在这个距离上,追猎者调查目标,以便计划进一步接近[50]运动,例如,通过估计相对轨道元素。在确定接近方向后,追踪者移动到目标附近(几米的距离),从那里机器人将执行最后阶段的捕获或操作[51]。一些视觉识别也可以在这个近距离会合[52]处进行。Rems, Risse和Benninghoff[53,54]为德国航空航天中心(DLR)航天器设计了一个GNC系统,在15米处开始近距离交会。当接近目标时,系统使用它的视觉能力(包括一个CCD相机,一个光飞时间相机和一个激光雷达传感器)来估计目标的姿态,保持目标在视线中并与之对齐。识别继续到8米的距离,在那里操作设备被部署。追逐者也在这个范围绕目标[55]飞行以识别接近方向,然后靠近(3米)以使目标在手臂到达。
2.2 目标识别
实时估计目标的运动和惯性特性是规划手臂的无碰撞路径和无损伤操纵目标的必要条件。当目标是非合作的时候,这个任务通常通过图像处理和基于模型的预测来完成。当为轨道上的运行卫星提供服务(例如机器人加燃料、对接或修理)时,这个阶段就不那么重要了,因为物体的运动和惯性参数是相对已知的。目标识别最简单的方法之一是使用基准标记[56]来识别目标上若干点的位置,这可以提供估算相对方向的几何手段。估计目标姿态和运动的最主要的技术是卡尔曼滤波(KF)[57]。最近,研究人员引入了三维视觉数据处理技术[58]进行识别,例如迭代最近点(ICP)算法[59]。其他更复杂的方法也被研究过,比如由Qureshi等人设计的认知控制系统[60],它结合了低水平(详细)特征跟踪和高水平推理,利用有限的信息进行更可靠的运动估计。
在某些轨道机器人操作中必须识别的目标的另一个特征是抓取或对接点,机械手将其锁定或对接到目标上。此类接触操作的例子包括清除碎片(debris removal)、加油(refueling)、对接(docking)和组装(assembly)。如果目标是合作的,这一点是先验的;然而,对于没有对接口的非协作目标,需要确定适当的抓取点。如Nenchev和Yoshida的研究中所讨论的,应该考虑的最重要的标准是使冲击时臂侧和目标侧的接触力和力矩最小化。他们利用反作用力零空间,通过感知末端执行器上的外力并估计它们对不同追逐器组件的影响来实现这一最小化。另一个识别标准是确保抓取点始终保持在跟踪机械手系统的视线范围内。第二个最值得注意的准则是,在整个手臂机动过程中必须估计抓取点的运动并更新其位置,因为末端执行器必须在手臂展开阶段结束时匹配抓取点的位置和速度。
2.2.1 视觉识别
视觉工具主要用于远程目标识别,特别是在轨机器人任务中。摄像机通常安装在跟踪航天器和末端执行器上,以确定目标的状态和特性[62]。Aghili等人的一个例子是利用带有3D视觉数据的ICP[63]。在他们的工作[63 66]中,他们集成了视觉系统,一个用动态状态估计器和最优控制方法来辅助近距离交会阶段的自主估计。利用冗余的方法,他们提出了一种在恶劣光照条件下获取3D图像的鲁棒方法。为此,他们使用了一种特殊的相机在一个单独的工作[65]。该方法结合三角测量、激光雷达传感器数据和基于模型的跟踪来获取目标的姿态和运动的视觉数据。作为扩展,他们后来添加了自适应扩展卡尔曼滤波器(EKF)来预测目标相对于跟踪航天器的相对平移和旋转运动[67]。这种状态和惯性估计器在有遮挡摄像机的情况下的性能也得到了验证[68]。
Shademan[69]提出了视觉伺服系统,该系统对目标模型和标定参数(摄像机的光学和构型参数)中的不确定性具有鲁棒性,能够处理在恶劣光照条件下表现良好的未知目标。该算法采用鲁棒M-估计器来确定描述运动的雅可比矩阵。W. Xu[70]提出了一种综合几何方法来估计目标的几何和状态使用立体视觉测量安装在手臂和跟踪航天器,而它与目标会合。Yazdkhasti还讨论了基于视觉的相对导航算法,以识别未知和翻滚的目标,并接近它[71]。Fourie等人对基于视觉的导航系统的性能进行了实验评估,用于自由漂浮目标的自主识别[72]。G. Arantes在他的论文[73]中讨论了一种使用KF进行序列状态估计的实时姿态和运动估计的视觉方法,并结合了一个单目摄像机系统。上述基于模型的方法不依赖于目标上的标记,适用于协同目标和非协同目标的识别。Oumer在他的论文中提出了一种鲁棒的基于特征的识别方法,通过在所有可见部分上合并点向运动模型,即使在缺乏足够特征的情况下,也能对目标的运动进行估计[74]。该方法消除了一些处理相机阳光反射的常见方法或依赖于激光雷达等重型传感器的复杂性。Shi和Ulric应用主成分分析(广泛用于数据处理)来估计邻近机动中未知卫星的位姿[75]。例如,e.Deorbit是一个最近的任务概念,它包含了跟踪和最小化位置误差的视觉伺服[76]。
2.2.2 卡尔曼滤波的使用
卡尔曼滤波器及其扩展形式是一种强大的估计工具,广泛应用于机器人系统在未知环境下的制导、导航和控制。F. Aghili的几篇论文[77]集中于使用激光视觉和KF来估计翻滚物体的运动,并跟踪其上的抓取点。卡尔曼滤波还可以与其他估计方法相结合以提高精度。Al-Isawi和Sasiadek[78]使用自适应无迹卡尔曼滤波器(AUKF)估计目标的动态状态,同时通过单应性方法提取特征点,采用ICP技术寻找质量中心,并结合模糊逻辑自适应控制来抑制干扰。自适应KF不仅可以帮助估计目标的状态,还可以估计其参数[79],如惯性矩、质心和旋转,以及主轴。该滤波器可以增强视觉识别系统,即使在视觉遮挡的情况下也能提供估计[68]。摄影测量法是与增强KF一起使用的另一种识别方法[80]。Zarei和Malaek[81]探讨了利用多个航天器进行目标识别的概念。他们提出了一种无迹的KF,以结合从卫星距离图像数据协调网络收集到的信息[882 84]。最近,Cavenago利用微分代数(DA)技术开发了无迹和扩展KF,用于姿态估计和接触检测目的[85]。
2.3 姿态同步
在近距离交会阶段,跟踪器与目标的相对直线运动是同步的。为了防止对接机构的损坏,对接航天器必须去除任何相对于目标的方向和角运动[86]。即使在其他机器人任务中,例如,一个机械手应该与目标接触,在追逐者和目标之间进行姿态同步有多个优势[87]:(i) 保持视线和协助目标识别;(ii) 简化手臂末端执行器的运动规划通过消除需要追逐的目标; (iii) 提高接触/对接性能通过减少接触力;(iv) 相比有完全驱动基础减少所需![]() (88、89)。这种同步在捕捉、解滚、对接或修复大型高速目标(如EnviSat脱轨[86])等任务中尤为重要。
(88、89)。这种同步在捕捉、解滚、对接或修复大型高速目标(如EnviSat脱轨[86])等任务中尤为重要。
2.4 机械手的部署
在轨机器人任务的主要阶段包括:从制动位置部署和自动运动控制机器人手臂,以达到目标的抓住点。这一阶段的挑战包括:(i) 避免碰撞与任何目标的一部分,追逐者或其他对象[41];(ii) 减少末端执行器之间的接触力[90]和目标到达抓点;(iii) 可靠地跟踪目标上的不同特性;(iv) 优化燃料/功耗[91];(v) 优化操作的时间[79,92]; (vi) 拒绝外部干扰效应[93,94];(vii) 考虑手臂和跟踪航天器的耦合动力学[95];(viii) 保持与控制站的遥测链接[96];(ix) 保持目标抓取点的视线。
机械手部署阶段的执行主要有两种方法:(i) 保持基地航天器静止;(ii) 让基地自由漂浮。前者的优点是与地面站保持更好的遥测连接,并面临一个相对容易的运动规划问题。机载AOCS系统可以保持基地卫星的方向不变[97,98],也可以利用副臂[95]补偿主臂运动引起的扰动。自由浮动的场景需要一个低![]() 但复杂控制臂的运动影响的位置和姿态基础[99]。在这种情况下,转移到基地卫星的反应和干扰通常应该进行补偿[100,101],或者可以设计一个二次机动[100],使基地回到其初始姿态并重新建立遥测链路。当计划保持跟踪器运动与目标同步时,必须提出一个并行的基端执行器控制[102]。
但复杂控制臂的运动影响的位置和姿态基础[99]。在这种情况下,转移到基地卫星的反应和干扰通常应该进行补偿[100,101],或者可以设计一个二次机动[100],使基地回到其初始姿态并重新建立遥测链路。当计划保持跟踪器运动与目标同步时,必须提出一个并行的基端执行器控制[102]。
2.5 捕获
在轨机器人任务的关键时刻是末端执行器在抓取点与目标接触的时刻。对由此产生的接触力进行补偿是这一阶段的主要挑战[103]。由于这些力是接触对方的相对速度的函数,在前一阶段,一个精确的运动规划者将这种相对速度降低到接近于零[90]是有利的。在最佳情况下,这些接触力在捕获时仍会出现[104];然而,防止它们伤害机器人系统或目标是至关重要的。研究人员要么在机械臂的运动规划中考虑影响[105],以最小化接触反作用力,要么在追逐机械臂系统处于最终配置以承受接触时设计末端执行器阻抗[106]。
2.6 捕获后作动
在捕获后阶段,将目标和追踪器置于相对配置中,以促进实现在轨机器人操作的主要目标,无论是修复(例如更换部件)[107]、加燃料[108]、结构组装[109]、重新在轨[110]或减少碎片[111]。在这个阶段的任务包括:(i) 重新翻滚或调整目标相对于追逐者的位置[112](例如通过把它的角动量转移到追逐器的补偿装置[113]), (ii) 定位和重新配置追逐-机械臂系统为最终任务目标做准备并建立遥测连接;(iii) 调整或僵直手臂[114]。捕获后机动的选择高度依赖于捕获阶段的规划[115116]。捕获后,追逐飞行器和目标要么像一个统一的动力物体[117],要么即使它们不严格连接,也具有显著耦合的动力学[118]。根据目标部分已知柔性部件的动力学特性[119][120]这一事实要求设计捕获后机动,用于联合系统的参数识别[121,122]。在进行系统辨识时,必须保证追逐机械手目标系统的稳定性和安全性[123]。
3. 航天器-机械臂系统运动学与动力学
航天器机械臂系统最好表示为由理想关节连接的刚体组成的多体系统。获得一个简单而又有几何意义的系统模型是至关重要的,它能够包括空间机械臂的区别特征。其中一个特性是拥有一个自由移动的6自由度(DoF)基座(航天器),从而在航天器和手臂之间产生耦合动力学[124]。基地航天器附着在一个或多个臂上,每一个臂上都有以刚体链为模型的多个连杆。最后一个连杆通常是用于操作目标的末端执行器。已经提出了许多形式来建模多体系统,其中用于运动学的旋量理论[125]和用于动力学的哈密顿/拉格朗日公式[126,127]由于其强大的几何基础而特别具有优势。本文采用旋量理论和拉格朗日公式对航天器机械臂系统的运动学和动力学进行了简要描述,为统一各种GNC方法的表述奠定了基础。在后面的部分中,将描述基于此公式的更高级的模型,这些模型添加了一些细微差别,或采用了适合捕捉系统的某些属性的全新方法。
在文献中,空间机械臂系统通常被建模为通过单自由度关节相互连接的刚体分支(如图6所示)。在空间机械臂的运动学和动力学分析中,始终假定为该模型。惯性坐标系和末端执行器由퐼分别标记![]() 。身体1,由
。身体1,由![]() 标记,是在各个方向自由移动的宇宙飞船,他的状态向量用
标记,是在各个方向自由移动的宇宙飞船,他的状态向量用![]() 表示。机械手是假定为具有n自由度的并且状态向量为
表示。机械手是假定为具有n自由度的并且状态向量为![]() ,空间机械臂系统的状态是通过向量
,空间机械臂系统的状态是通过向量![]() 定义。相对躯体i,对躯体j的姿态可以用齐次变换:
定义。相对躯体i,对躯体j的姿态可以用齐次变换:
其中
![]() 是躯体i和躯体j之间的相对姿态,
是躯体i和躯体j之间的相对姿态,![]() 是从躯体j到躯体i的位移并且前上标j表示该向量在躯体j的坐标系中表示,描述末端执行器相对于惯性坐标系的位置和姿态的正运动学映射为:
是从躯体j到躯体i的位移并且前上标j表示该向量在躯体j的坐标系中表示,描述末端执行器相对于惯性坐标系的位置和姿态的正运动学映射为:
![]()
每个变换都依赖于描述两个相互连接的物体之间相对位姿的关节参数,这是一个基座的向量![]() 和机械手的第i个关节
和机械手的第i个关节![]() ;因此,
;因此,![]() 。
。
一个相对扭转![]() 描述在惯性坐标系中的第i个物体相对于第物体的无限小相对运动。雅可比
描述在惯性坐标系中的第i个物体相对于第物体的无限小相对运动。雅可比![]() 是在惯性坐标系下,由机械手关节的速度和基座的速度到末端执行器速度对应的相对扭转
是在惯性坐标系下,由机械手关节的速度和基座的速度到末端执行器速度对应的相对扭转![]() 的映射,其形式如下[125]:
的映射,其形式如下[125]:
![]()
其中,![]() ,如果将基体速度视为基体瞬时扭转,并且
,如果将基体速度视为基体瞬时扭转,并且![]() 由列
由列![]() 组成,
组成,
在这里任意齐次变换![]() ,伴随算子
,伴随算子![]() 被定义为:
被定义为:
其中上标和下标分别表示从一个向量到相应的斜对称矩阵及其逆矩阵的映射。注意,当上标或者下标等于0或n指的是基体(b)或末端执行器(ee)。每物体相对于惯性坐标系的相对扭转,并在惯性坐标系中表示,然后由下式给出:
![]()
使用基体速度和阐明航天器机械臂的运动学的解释方法,系统的动力学可以通过拉格朗日方法表示为:
这里,![]() 是一个6×6的质量矩阵,其对应于在系统配置
是一个6×6的质量矩阵,其对应于在系统配置![]() 时整个宇宙飞船机械手系统,
时整个宇宙飞船机械手系统,![]() 是n×n的广义质量矩阵对应的机械臂,并且
是n×n的广义质量矩阵对应的机械臂,并且![]() 是个6×n的矩阵代表了基体和机械臂之间的耦合的惯性。质量矩阵定义如下:
是个6×n的矩阵代表了基体和机械臂之间的耦合的惯性。质量矩阵定义如下:
其中,![]() 是一个躯体l的常惯性矩阵,定义在其自身坐标系中。
是一个躯体l的常惯性矩阵,定义在其自身坐标系中。![]() 表示矩阵
表示矩阵![]() 的第j列,
的第j列,![]() 表示矩阵
表示矩阵![]() 的第i行第j列元素。
的第i行第j列元素。![]() 分别为基体航天器和第个机械臂连杆对应的雅可比矩阵的矩阵块,表示在惯性坐标系中。
分别为基体航天器和第个机械臂连杆对应的雅可比矩阵的矩阵块,表示在惯性坐标系中。
同样,分块![]() 和
和![]() 分别是科氏力和离心力的矩阵对应于整个系统和机械手。科里奥利耦合和离心作用被
分别是科氏力和离心力的矩阵对应于整个系统和机械手。科里奥利耦合和离心作用被![]() 描述。设M为所有质量矩阵的集合和C为科里奥利和离心矩阵块的集合。C矩阵的元素被定义为:
描述。设M为所有质量矩阵的集合和C为科里奥利和离心矩阵块的集合。C矩阵的元素被定义为:
其中,![]() 是向量
是向量![]() 的第k个元素。向量
的第k个元素。向量![]() 为基体和机械手自由度对应的势能,分别为:
为基体和机械手自由度对应的势能,分别为:
其中,![]() 是作用于系统的外势场。
是作用于系统的外势场。![]() 和
和![]() 分别为基座和机械臂中控制方向的集合。最后,向量
分别为基座和机械臂中控制方向的集合。最后,向量![]() 和
和![]() 分别表示基座和机械手的控制输入。
分别表示基座和机械手的控制输入。
4. GNC用于姿态同步
如2.3节所述,角度运动同步的优势有以下几个原因:增强目标识别(enhanced target identification)[86],改进手臂轨迹规划(improved arm trajectory planning)[87]和控制,实现无损伤接触(performing demagefree)和燃料节约(fuel conservation)[88,89]。Colmenarejo及其合作者对机器人在轨操作中的线性\角运动同步进行了广泛的讨论[87]。他们提出了3种场景:(i) 在整个手臂操作过程中保持跟踪器在选定抓取点前静止;(ii) 通过使跟踪器绕目标的旋转轴被动旋转,使末端执行器相对于抓取点保持静止;(iii) 只保持跟踪器在轨道(非旋转)坐标系中静止,并主动控制机械手运动以跟踪抓取点。在第一个场景中,追捕者必须方法目标对其自旋轴,然后在遵循把握点这将导致最复杂的手臂运动,但需要最高![]() 。该方法最适用于快速旋转目标。第二种情况的手臂运动稍微复杂一些,但燃料消耗更少。这种方法最适用于具有固定旋转轴的缓慢旋转目标。第三种情况需要最复杂的手臂控制,由于需要可能的循环运动,它可能比前一种情况需要更多的能量,特别是当目标快速旋转时。这种方法对静止目标最有效。第一个方案的GNC方法已在[89128]中开发出来。Welsh和Subbarao开发了一种自适应控制算法,将同步过程分解为两个线性和旋转阶段:(i) 沿着目标对接点的方向,在追逐器和目标之间保持一个安全的相对线性位置;(ii) 重新定位跟踪航天器的姿态,以对准机载机器人设备与恒定的相对位置矢量对齐[89]。他们后来设计了一个能抵抗环境干扰的非线性控制器来完成上述的同步任务[88]。在这项工作中,他们利用一个虚拟参考目标来指挥所需的跟踪姿态。同样,Yan-wei和leping开发了一种两阶段6自由度同步过程,采用了一种对内部不确定性具有鲁棒性的自适应控制方法,其具体目的是减少手臂的操作时间[128]。
。该方法最适用于快速旋转目标。第二种情况的手臂运动稍微复杂一些,但燃料消耗更少。这种方法最适用于具有固定旋转轴的缓慢旋转目标。第三种情况需要最复杂的手臂控制,由于需要可能的循环运动,它可能比前一种情况需要更多的能量,特别是当目标快速旋转时。这种方法对静止目标最有效。第一个方案的GNC方法已在[89128]中开发出来。Welsh和Subbarao开发了一种自适应控制算法,将同步过程分解为两个线性和旋转阶段:(i) 沿着目标对接点的方向,在追逐器和目标之间保持一个安全的相对线性位置;(ii) 重新定位跟踪航天器的姿态,以对准机载机器人设备与恒定的相对位置矢量对齐[89]。他们后来设计了一个能抵抗环境干扰的非线性控制器来完成上述的同步任务[88]。在这项工作中,他们利用一个虚拟参考目标来指挥所需的跟踪姿态。同样,Yan-wei和leping开发了一种两阶段6自由度同步过程,采用了一种对内部不确定性具有鲁棒性的自适应控制方法,其具体目的是减少手臂的操作时间[128]。
虽然没有明确地集中在追逐者机械臂系统上,但在在轨对接和卫星编队飞行的姿态同步方面有大量的工作[129,130],这些工作可以扩展到其他在轨机器人任务。Wang, Hadaegh和Lu[131]证明了即使是一个简单的PID控制器也能够协调多个自由漂浮卫星的相对姿态和直线运动。机器人航天器的姿态同步必须对系统辨识和环境干扰产生的不确定性具有弹性。Li和Kumar[132]提出了一种集中滑模控制,用于编队飞行场景中的跟踪任务,其中卫星跟踪一个主航天器,模糊自适应控制器考虑了系统的不确定性。Wu, Wang和Poh[133]也采用滑模控制结构来分散控制问题,并在存在不确定性的情况下分别同步多个航天器编队飞行的姿态。由非线性反馈控制逻辑和补偿器组成的复合控制律被An、Lu和Ren[134]证明了用于对接姿态同步的鲁棒性。Chung, Ahsun和Slotine[135]提出了一种振荡器相位和拉格朗日量的分散跟踪控制律,实现了航天器编队姿态和线性运动的并行非线性控制。这种能力尤其有利于捕获任务处理复杂的翻滚运动的目标,需要飞行和轴向同步。
还研究了在轨服务任务中对接的姿态同步问题。例如,Subbarao和McDonald利用多传感器融合导航技术来规划交会对接[136]。Subbarao和Welsh提出了自适应同步,以在对接或捕获自由漂浮的航天器时保持相对位置和适当方向[88]。Yun-hai等人开发了一种自适应跟踪控制,在非合作目标OOS时实现跟踪器姿态与目标姿态的同步[137]。Xueyan, Zhang和Wei还设计了一种基于终端滑模控制方法的对接翻滚目标的姿态同步控制律[138]。Lu, Geng和Shan的工作提出了一种通过鲁棒最优滑模控制方案实现对翻滚轨道物体自主对接的过程[139]。
5. GNC用于手臂控制
如第2.4节所述,手臂运动的GNC是在轨机器人任务研究的核心焦点之一。不能独立于航天器的运动来研究机械臂的运动。针对这种耦合系统的轨迹规划已经得到了广泛的研究[140 142]。由于轨道跟踪任务的鲁棒性和稳定性在在轨任务中至关重要,因此闭环控制系统也得到了深入的研究[143 145]。在这一阶段,追逐者臂系统的初始配置和速度由追赶器在交会或同步阶段结束时的终端状态所决定[137,139]。此外,末端相对条件,即末端执行器在捕获点的位置,由识别阶段指定[68,69,79,146]。同时,基体航天器与手臂之间的耦合动力学[147]以及环境影响[143]是手臂GNC中考虑的主要因素。
任务策划者要么主动保持基地卫星站在整个手臂运动(自由飞行场景(free-flying scenario))[148],要么为基地分配一个预先设计的被动或主动轨道[149],要么允许基地自由移动(自由浮动场景(free-floating scenario))[97]。在文献中,对自由飞行和自由漂浮场景的研究最多。固定基地需要解决站位保持问题[87],而另一方面,自由漂浮的航天器手臂引入了非完整臂轨迹规划[118]和控制的挑战。科学界的共识是,当末端执行器与目标接触时,ADCS系统应该关闭,以避免控制系统的任何意外响应。因此,总是有必要为机器人系统规划一个自由漂浮的场景。在自由漂浮的情况下,文献中讨论的主要问题是最小化由手臂运动引起的对基地航天器的干扰。然而,在自由飞行系统中,主要的问题是在保持遥测链路稳定的同时尽量减少功率消耗[91]。由于手臂动力学的非完整性,如动力学奇点[150,151]和平滑避障的需要[152,153],也可能带来其它挑战。当广义雅可比矩阵[154](见第5.1.2节)变为奇异时,就会出现动态奇异。Tchon, Respondek和Ratajczak利用控制仿射系统描述的非完整机器人的正规奇异形式解决了这个问题[151]。在任务概念层面上,设计一种能够适应各种任务的航天器臂系统是理想的。重构(Reconfiguration)、模块化(modularity)[155,156]、变结构控制(variational-structure control)[40,157]、鲁棒性和适应性(robustness and adaptability)[158 160],或使用多个机械手(multiple manipulators)[161]可以满足这一需求。Aghili等人提出了一种可重构手臂,该手臂具有多个被动关节,可锁定在特定构型中[155,156]。挑战可能来自追逐臂系统及其环境中的不确定性,例如,目标模型中的不确定性[121],机器人系统或目标中的未计算弹性行为[162,163],以及外部和内部扰动[164,165]。因此,能够处理不确定性的先进控制方法,如自适应、鲁棒和滑模控制器[166 168]在航天器机械臂系统的文献中得到了广泛的研究。表1收集了本节中介绍的GNC方法背后的核心思想,并比较了它们的性能。
5.1 基体飞船在自由浮动
自由漂浮空间机器人的控制比自由飞行机器人更复杂,因为其基座是非驱动的6自由度[171]。这是一个数学问题,类似于多体系统中某些关节失去驱动能力[172]。一方面,非驱动为系统的轨迹规划和控制带来了挑战,另一方面,它可以利用内部耦合和系统的可控程度开发节能控制策略[173]。航天器与目标质心之间的初始相对位置是另一个通常被忽略的因素,由于整个航天器臂系统在轨道框架内的质心是静止的(除非考虑干扰),因此在路径规划中成为关键因素[175]。基于第3节的公式动力学,描述自由漂浮航天器臂系统运动的一般动力学方程不包括对基地的任何应用控制命令。在文献中,通常忽略任何势的局部效应,如重力和地球磁场,而不考虑扰动。因此,空间臂系统的动力学方程可以改写为
由于假设系统不受外力/力矩作用,系统在惯性坐标系下的总动量守恒:
通常的做法是保持动量为零:
![]()
在零动量系统中,基座的姿态依赖于机械手关节所走的路径。将臂从一个起始配置带到一个结束配置的两种不同路径可能导致不同的卫星姿态[176]。然而,一些研究人员,如Seweryn和Sasiadek,发展了轨迹优化方法,其考虑到基地航天器的非零角动量或作用在其上的外力[177,178]。在手臂的控制和轨迹规划中感兴趣的特性主要是末端执行器的绝对角速度和线速度。
在各种研究工作中,已经探讨了自由漂浮空间机械臂路径规划的挑战。Ulrich和其合作者将简单反馈控制器(如PID逻辑)的轨迹跟踪能力与更先进的控制方法(如自适应控制方案)进行了比较[158]。在自由漂浮机器人的控制中,一个常见的解决难题是如何处理作用在基体航天器上的反应[124]。自适应和鲁棒控制器为解决不必要的基运动问题提供了强有力的手段[179]。Dimitrov研究了由于基座和机械手动力学之间的耦合而产生的几个问题,专门用于规划无反应的手臂机动。他引入了完整分布控制,将偏置角动量和分布动量控制用于捕获后规划[147]。AlIsawi使用自适应无迹KF和单应矩阵来估计目标的未知惯性和姿态,他提出了一种自适应模糊逻辑系统来控制自由漂浮的航天器手臂系统[78]。在下面的章节中,将研究自由浮动系统的轨迹规划和控制的几个解决方案。
5.1.1 优化控制
在一个最优控制策略中,命令信号的选择使选择的性质最优,同时使所描述的系统通过空间机械臂动力学方程中从一个起始条件![]() 到最后一个条件
到最后一个条件![]() [180]。考虑的成本函数通常是一个依赖于状态轨迹和系统的控制输入的函数[181,182]:
[180]。考虑的成本函数通常是一个依赖于状态轨迹和系统的控制输入的函数[181,182]:
其根据动力学优化
成本或性能指标包括两个部分:(i) 一个端点成本![]() 依赖于边界条件的轨迹;(ii) 一个积分项成本包括拉格朗日
依赖于边界条件的轨迹;(ii) 一个积分项成本包括拉格朗日![]() ,其取决于状态和控制命令的演变[183]。运行时间、燃料成本、基体扰动和路径长度是空间机器人控制中常见的成本函数。
,其取决于状态和控制命令的演变[183]。运行时间、燃料成本、基体扰动和路径长度是空间机器人控制中常见的成本函数。
在Aghili等人的一系列工作中,提出了前抓和后抓机动的最优控制公式[119,184]。成本函数的提出旨在减少操作的时间![]() ,手臂末端执行器的线性运动在基体飞船坐标系(
,手臂末端执行器的线性运动在基体飞船坐标系(![]() ),控制命令(
),控制命令(![]() )和燃料成本[118185]:
)和燃料成本[118185]:
其中,![]() 是末端执行器相对于的位置,并在基本航天器坐标系中表示。
是末端执行器相对于的位置,并在基本航天器坐标系中表示。
这个公式产生最优控制信号为:
其中![]() 的演变规律为:
的演变规律为:
由微分方程得到最优轨迹:
粒子群优化(PSO)是另一种常用的在轨机器人任务优化技术[95,186]。粒子群是一组优化向量[112,187],每个向量包含性能参数,如燃料成本和关节运动参数[187,188],然后经过一系列小规模的优化步骤。成本函数的一种选择是根据手臂运动对航天器施加的扰动,这种扰动需要耗费额外的燃料并造成遥测链路的损失。在Zhang等人的研究中,通过粒子群算法进行轨迹优化,以最小化对基地航天器的干扰[186]。在Xu提出的另一种方法中,采用遗传算法(GA)来寻找同时控制手臂和基体的最优路径[70,189]。另一个使用遗传算法的例子可以在Huang, Chen和Xu的工作中看到[190],该工作生成了对基体施加最小干扰的最优轨迹。当采用柔性连杆来利用其非线性行为或更好地模拟手臂时(见5.6节),系统会引入不必要的弹性振动,而这种振动通常应该被最小化[162]。Jankovich和Kirchner在其非线性轨迹优化技术中通过正交配置方法利用基体和手臂之间的耦合来最小化系统的总角动量[191]。
另一种最优控制技术,基于Piazzi和Visioli的工作[192],旨在找到最小化关节速度和基体方位(急动)的二阶导数的手臂路径。这种方法的优点,区别于其他最优控制技术,在于其生成的轨迹与人体运动的相似性,并且它对振动体现出了弹性。该方法中的成本函数被定义为系统中需要最小化的总跳动。这种方法考虑的轨迹是分段连续曲线,通常用每个自由度的多项式来表示。
在早期的尝试中,DeSilva也提出了一种基于加速度和加速度限制的轨迹规划器[193],利用了空间机械臂的冗余性。可以应用各种优化技术来提高该策略的性能。急动度也可以是多目标优化中的部分性能指标[194]。急动度最小化已经被Huang[195,196]引入以提高基于遗传的最优控制的效率。GA优化(类似于PSO)遵循图7所示的过程。
5.1.2 广义雅可比矩阵与反应零空间
一些开创性的运动基机械手控制方法引入了Yoshida和Umetani[154]首先提出的广义雅可比矩阵(GJM)[197]的概念。他们进一步分析和测试了该工具,鼓励许多其他研究人员将其用于运动学、动力学和控制分析[198]。自由浮动系统通常被认为是最初在放松,在这种方法中动量保持常数为零,也就是说,动量方程中const=0。因此,
![]()
带入扭转公式:
![]()
和GJM
![]()
当系统动量为零时,该雅可比矩阵将关节运动与末端执行器运动直接联系起来。Nenchev和Yoshida后来通过引入偏置角动量方法对该方法进行了改进,该方法基于在规划手臂轨迹时最小化基本运动[199]。他们也使用相同的视点来缩小后捕捉的基本运动[61,200]。GJM的概念也可以用来分析运动基机械手的工作空间。Yoshida和Umetani使用了从GJM公式中提取的保证工作空间(GWS)来测试和证明他们的方法的适用性[201,202]。
引入反应零空间(RNS)作为确定关节速度的工具,使作用在基底[20]上的反应最小。将机械手的状态进行划分,以利用系统的冗余性和RNS所产生的1维度分布的可积性,在基上引入零反作用轨迹[203]。引起零反应的关节加速度有以下形式:
![]()
其中,![]() 是矩阵A的伪逆,
是矩阵A的伪逆,![]() 是投影的零空间
是投影的零空间![]() ,而
,而![]() 是一个任意的向量。Kaigom使用时变多项式来张成RNS的一组基,并在这个空间中表示关节速度。然后他使用约束粒子群优化方法来寻找最优的联合轨迹[95]。Nenchev等人开发了一种用于安装在柔性基上的机械臂工作空间路径跟踪的复合控制器,例如利用RNS避免对柔性基的干扰[204]。许多控制技术建立在上述方法的基础上,以利用它们的简化公式。例如,采用基于遗传算法的优化来解决系统的非完整性[189],引入了利用系统冗余性的最优解[203 205],提出了一种用于空间机械臂系统的数字控制方案[206],控制技术被建议将机器人概念解决方案扩展到安装在柔性基础结构上的机械臂[207]或并联或协调工作的多个机械臂[208]。
是一个任意的向量。Kaigom使用时变多项式来张成RNS的一组基,并在这个空间中表示关节速度。然后他使用约束粒子群优化方法来寻找最优的联合轨迹[95]。Nenchev等人开发了一种用于安装在柔性基上的机械臂工作空间路径跟踪的复合控制器,例如利用RNS避免对柔性基的干扰[204]。许多控制技术建立在上述方法的基础上,以利用它们的简化公式。例如,采用基于遗传算法的优化来解决系统的非完整性[189],引入了利用系统冗余性的最优解[203 205],提出了一种用于空间机械臂系统的数字控制方案[206],控制技术被建议将机器人概念解决方案扩展到安装在柔性基础结构上的机械臂[207]或并联或协调工作的多个机械臂[208]。
5.1.3 虚拟机械手的方法
Vafa和Dubowsky首先提出了虚拟机械臂(VM)的概念[99],作为一种分析方法来研究基体航天器和机械臂之间耦合的退化动力学效应。虚拟机是一种假想的固定基机械臂,动态等效于安装在航天器上的手臂。由于它是固定的底座,传统的方法可以用来分析自由漂浮物体上的手臂的动态行为或为这种系统设计控制器[209]。手臂、底座和有效载荷的运动学可以用虚拟机械臂的运动来表示[210]。虚拟机以航天器机械臂系统的质心(CoM)为基础。如果没有外力作用于该系统,则有可能将惯性系置于系统的CoM处,因此VM的基底保持静止。这个静止点被称为虚拟地面(VG)[99]:
其中,![]() 显示第i根连杆的CoM的矢量位置而
显示第i根连杆的CoM的矢量位置而![]() 是基体的,
是基体的,![]() 代表第i根连杆的质量而
代表第i根连杆的质量而![]() 是基体的,
是基体的,![]() 是VG的位置矢量。虚拟臂的第一个关节是一个球关节,它代表了基体卫星的方位,其余的关节与真实的手臂对应。虚拟机的每个转动关节都有一个与实际机械臂中等效关节平行的旋转轴,并旋转相同的角度[211]。每个连杆的VM,由向量
是VG的位置矢量。虚拟臂的第一个关节是一个球关节,它代表了基体卫星的方位,其余的关节与真实的手臂对应。虚拟机的每个转动关节都有一个与实际机械臂中等效关节平行的旋转轴,并旋转相同的角度[211]。每个连杆的VM,由向量![]() 定义:
定义:
![]()
其中,
其中,![]() 是第i个连杆的CoM到下一个关节的向量,
是第i个连杆的CoM到下一个关节的向量,![]() 是从同一个关节到下一个连杆的CoM的向量,如图8所示。
是从同一个关节到下一个连杆的CoM的向量,如图8所示。
因此,VM的关节的位置不同于真正的手臂,但是末端执行器的位置在VM总是与实际末端执行器的位置一致(![]() )[210]。
)[210]。
![]()
Dubowsky和Papadopoulos利用虚拟机械臂的概念设计了简化相空间的线性控制器[172],并研究了自由漂浮空间机械臂的动态奇异性[150]。Parlaktuna和Ozkan利用虚拟机械臂概念开发了一种自由漂浮空间机械臂关节空间的自适应控制方法[212]。虚拟机械臂对于经验测试特别有用,因为它有助于建立一个与自由漂浮机器人模拟器等价的固定基机器人模拟器[213]。Torres和Dubowsky利用虚拟机械臂的概念来开发扰动图[100]。他们提出了一种计算效率高的手臂路径规划方法,利用机械臂冗余最小化对基地航天器的干扰[214]。他们还展示了这种方法产生路径规划和控制策略的能力,以最大限度地减少手臂与其移动底座之间动态耦合的负面影响[101]。他们开发了一个二维臂的图形表示,显示了导致基地航天器在关节构型空间的每个点上产生最大或最小扰动的运动。利用式(32),航天器姿态的微小变化可以表示为微小机械臂关节运动的函数。由于航天器的姿态在一般情况下具有较高的重要性,因此研究人员主要关注航天器的微小姿态变化。Dubowsky解的结果也可以作为更精确、更繁琐的数值方法的初始点[214]。他还将该方法从两自由度扩展到多关节系统[100,215]。在增强扰动映射中,存在对航天器的扰动始终为零或最小的路径。该图用于在扰动图中找到零扰动路径或避免高扰动区域的路径[100](图9)。
5.2 基体航天器受控(自由飞行)
自由飞行的航天器手臂系统不是固定在地面上,但他们的方向是通过控制力矩陀螺仪,动量轮和推进器等手段保持控制。一个值得注意的早期概念是用于操纵轨道上其它物体的自由飞行机器人ROBIN,它是由Bronez和Clarke为国际空间站[5]开发的。另一个值得注意的自由飞行的例子是由日本NSADA设计的工程测试卫星VII (ETS-VII),它携带一个六自由度的手臂,作为几种GNC方法的测试平台[176]。这样的系统不再是欠驱动的。但是,它需要额外的燃料来保持遥测联系和抑制干扰。其动力学模型除了手臂控制输入外,还包含了基本控制力,总动量不再是恒定的。航天器要么通过一个完全在线的AOCS系统控制,要么只补偿基体上的小扰动。Ellery研究了单臂自由飞行航天器的运动学和动力学及其基体上的扰动[124]。Huang等人利用具有在线AOCS的自由飞行航天器的静止基座,以类似于固定基座机器人的方式为其机械臂设计离散轨迹规划器[97]。Rybus和Seweryn研究了自由漂浮和自由飞行航天器手臂系统之间的差异[98],研究了轨迹优化[216],应用Bezier曲线避免奇异[92],以及两种情况下的捕获机动[98]。带有一些非驱动关节的自由飞行系统仍然可以被控制和稳定[217]。Aghili等人提出、设计并建模了用于在轨服务的受控航天器上可重构的6自由度机械臂[156]。他们提出的手臂通过锁定和解锁特定的圆柱形关节来改变配置[155],以匹配捕获任务的各个阶段的要求,即:(i) 延长伸展,(ii) 改善避障,(iii) 从发射配置切换到部署配置[218]。他们还通过仿真进一步证明了该设计的性能。
5.2.1 优化控制
优化技术也被用于自由飞行航天器机械臂的控制[216]。Lampariello结合了非线性优化和查表来寻找最优控制,该最优控制对应于代表机械手总机械能的成本函数[219]:
临近关节极限,除了是问题的约束,也可以包括在成本函数中[148]。Aghili设计了一个协调最优控制器,用于捕获非合作目标的机器人任务的捕获前和捕获后阶段,在控制基础航天器的同时生成最优手臂轨迹[118,184]。Seddaoui和Saaj开发了一种使用遗传算法的自由飞行航天器机械臂系统的最优路径规划算法,该算法利用航天器的受控运动来提高手臂运动的安全性[220]。
5.3 多臂的使用
机械臂的运动可用于控制基体航天器的方向或抑制干扰。这个想法的根源可以追溯到Vafa和Dubowsky的提议,计划手臂的循环运动来重新定位基地航天器[99],利用基地和手臂之间的耦合效应。K. Yamada验证了这个想法,证明了基体航天器的方位可以在特定的方向上改变,通过让手臂通过特定的轨迹[221,222]。Suzuki和Nakamura利用双向方法扩展了这一思想,仅通过驱动9自由度航天器机械臂的6自由度来解决非完整路径规划问题[223]。Schulz讨论了一种特殊的情况,即当基地卫星通过特定的v形轨迹接近目标时,通过手臂的运动来确定基地卫星的方向,而无需执行循环运动[224]。利用这一想法的一种方法是使用安装在单个航天器上的多支手臂,用一只手臂同时执行一项任务,用另一只手臂控制基座不必要的运动[225]。Moosavian和Papadopoulos给出了安装在基地航天器上的N臂的自由漂浮机器人的一般动力学方程为[226]:
其中,![]() 是第k条机械臂的第j个躯体的雅可比,
是第k条机械臂的第j个躯体的雅可比,![]() 是第k条机械臂的连杆数。
是第k条机械臂的连杆数。![]() 是第k条机械臂的第j个躯体的外力[226]。这样,
是第k条机械臂的第j个躯体的外力[226]。这样,![]() 必须包括所有手臂的自由度。Yoshida等人开发了多臂航天器的广义雅可比矩阵:
必须包括所有手臂的自由度。Yoshida等人开发了多臂航天器的广义雅可比矩阵:
![]()
其中,![]() 是第k条手臂的GJM,
是第k条手臂的GJM,![]() 是第k条手臂的机械臂雅可比,
是第k条手臂的机械臂雅可比,![]() 是基体运动对第k个末端执行器速度的贡献的雅可比矩阵。尽管
是基体运动对第k个末端执行器速度的贡献的雅可比矩阵。尽管![]() 只是第k条机械臂中关节参数的函数,但是
只是第k条机械臂中关节参数的函数,但是![]() 包括其他手臂对底座的影响从而对第k个末端执行器运动的影响。Yoshida等人基于该GJM公式的转矩优化控制方法[227],开发了一个稳定机械臂控制器[228]。Moosavian和Papadopoulos多臂机系统的运动学进行了分析,提出了两种不同的方法制定其相关的运动学,并且得到了第k条手臂的第i个连杆的相对于关节的速度雅可比矩阵[229]。他们提出了两种不同的基于模型的控制器和一种基于转置雅可比矩阵的方法[161],用于同步多个手臂的运动,从而同时最小化基座上的干扰并达到目标。基于PD控制器的第k个末端执行器位姿误差
包括其他手臂对底座的影响从而对第k个末端执行器运动的影响。Yoshida等人基于该GJM公式的转矩优化控制方法[227],开发了一个稳定机械臂控制器[228]。Moosavian和Papadopoulos多臂机系统的运动学进行了分析,提出了两种不同的方法制定其相关的运动学,并且得到了第k条手臂的第i个连杆的相对于关节的速度雅可比矩阵[229]。他们提出了两种不同的基于模型的控制器和一种基于转置雅可比矩阵的方法[161],用于同步多个手臂的运动,从而同时最小化基座上的干扰并达到目标。基于PD控制器的第k个末端执行器位姿误差![]() ,转置雅可比矩阵方法简单地使用GJM生成控制命令[230]
,转置雅可比矩阵方法简单地使用GJM生成控制命令[230]
![]()
其正定矩阵![]() 分别包括比例增益和导数增益。
分别包括比例增益和导数增益。
多臂也可以协调控制以协同执行一项任务[231]。GNC方法已被开发用于使固定底座多臂机器人协调地处理目标[232],跟踪轨迹[233],绕过复杂的环境约束[234],在装配过程中匹配零件并控制对目标施加的力[235]。在空间机器人领域,Zhao等人开发了一种基于计算力矩法和GJM的零内力协调控制器来抑制自由漂浮欠驱动航天器机械臂系统的基体扰动[236]。Yoshida等人研究了空间机器人中多臂的协调控制[228],发展了稳定臂的概念。当主臂接近目标时,Huang利用副臂来平衡航天器[237,238]。另一方面,Shi等人在存在不确定性的情况下,控制空间机器人的双臂捕获单个浮动目标[239]。根据任务的不同,多臂机械手可以从中央决策单元[240]、主从位置\力控制器[241]或去中心化控制逻辑[232,242]中获益。Yoshida等人比较了安装在航天器上的双臂的单独控制和协调控制[208]。双臂自动协调控制的实用性已由Zhou[243]进行了实验验证。
5.4 自适应控制
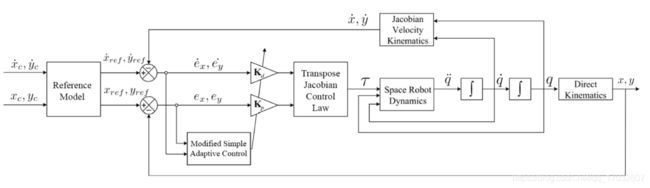
自适应控制方案由于具有根据外部和内部变化进行自我调整的能力,在应对未知环境和非合作目标时非常有利。Walker利用自适应控制器来实现稳定,尽管航天器机械臂系统的动态和惯性参数存在不确定性[244]。Wang和Hanlei在自适应逆动力学研究中引入了广义动力学回归器,以考虑未知参数或参数变化引起的非线性[245]。Wee等人通过自适应逻辑通过动量积分获得参数估计,演示了自适应控制方法同时控制自由漂浮航天器和6自由度手臂的轨迹的能力[246]。Ulrich和Shi证明了一种自适应控制器能够在不需要在线估计的情况下处理大惯性不确定性[247]。Ulrich等人也开发了一种基于无源输出反馈的自适应控制律,以提高航天器手臂系统路径规划器的稳定性和鲁棒性[248]。较简单的自适应控制逻辑被证明是控制空间机械臂的有效方法,尽管它们很简单[249]。Ulrich等人用如图10所示的配置评估了一个简单的自适应控制器的性能[168]。自适应控制器操作的基础上调整控制增益的基础上收到的反馈,从动态系统的输出。Ulrich等人提出了一种基于输出反馈转置雅可比矩阵控制律的直接自适应控制(DAC)[168](图10)
![]()
其中为末端执行器位置误差。一个由Ulrich为其改进的简单自适应控制器(MSAC)提出的自适应逻辑是[168]
![]()
和
其中,![]() 是控制设计师设计的控制参数,
是控制设计师设计的控制参数,![]() 是小的正调节系数用于防止控制增益的积分项发散[168]。另一种常见的自适应控制方法,称为模型参考
是小的正调节系数用于防止控制增益的积分项发散[168]。另一种常见的自适应控制方法,称为模型参考
自适应控制(MRAC),包括一个参考模型,并将模型的输出![]() 和一个标量参考模型输入信号
和一个标量参考模型输入信号![]() 合并到整体控制信号中[250]
合并到整体控制信号中[250]
控制增益通过
其中,![]() 和
和![]() 都是控制参数,并且
都是控制参数,并且![]() 分别为误差、系统模型输出和模型输入对应的增益[250]。
分别为误差、系统模型输出和模型输入对应的增益[250]。
Cao和Silva在具有柔性关节和连杆的空间机器人路径规划中使用神经网络辅助他们的自适应控制器[251]。闭环自适应控制需要一个带有可靠状态估计的感觉系统。Ulrich和Sasiadek将EKF与自适应控制器耦合[252],针对关节处具有弹性不确定性的机械臂开发了自适应反馈前馈控制器[159]。他们演示了直接自适应模糊控制跟踪模型和真实空间机器人之间误差的适应能力[253]。Sasiadek和Green也应用模糊逻辑系统来适应柔性连杆机器人转置雅可比控制器的增益[254]。李振宇提出了一种基于虚拟机和最小二乘估计技术的未知质量属性自由漂浮空间机器人自整定自适应控制方案[255]。Shibli, Su和Aghili开发了一种基于自由飞行空间机械臂逆动力学的自适应控制器来执行接触操作[256]。
5.5 滑模控制
变结构/混合型控制器能够根据系统的变化在控制律的增益集之间切换,从而产生对扰动和不确定性的弹性[257]。最著名的非线性变结构控制是滑模控制(SMC)[258]。SMC利用状态反馈将系统从初始状态驱动到状态空间中的滑动面,并通过始终指向滑动面的开关控制输入使系统保持在滑动面附近的窄带内[258]。与滑动面相切的平滑控制输入保证了系统在平衡点处的稳定性。滑动面的选择和将系统推向滑动面的控制逻辑决定了控制器的行为。SMC,最近被研究用于空间机器人的应用,在控制非线性系统和固定基机器人手臂的文献中得到了广泛的讨论[259]。Lin, Zhu和Cai提出了一种基于SMC的混合控制器,将欠驱动2-DoF机器人机械臂系统分解为两个子滑动面[260]。Ashrafioun和Erwin开发了一种欠驱动多体系统的滑模控制方法,将滑动面定义为驱动和非驱动状态跟踪误差的线性组合[261]。他们将由式(17)[261]定义的自由漂浮空间机械臂系统动力学重新安排为
其中,![]() 包括离心和科里奥利效应,以及保守力和非保守力。求解加速度,并将滑移面s定义为为驱动状态
包括离心和科里奥利效应,以及保守力和非保守力。求解加速度,并将滑移面s定义为为驱动状态![]() 、未激励状态
、未激励状态![]() 的跟踪误差以及它们导数的线性组合:
的跟踪误差以及它们导数的线性组合:
![]()
则提出以下控制律:
此处,![]() 是决定滑动面的控制器参数,
是决定滑动面的控制器参数,![]() 表示模型参数
表示模型参数![]() 的估计,Ashrafioun和Erwin定义的一些广义质量矩阵和力向量[261]。添加
的估计,Ashrafioun和Erwin定义的一些广义质量矩阵和力向量[261]。添加![]() 作为积极推动系统向滑动表面的抖振控制输入。
作为积极推动系统向滑动表面的抖振控制输入。
SMC仍然是航天器机械臂系统控制的一个有待开发但很有前途的方法。Yinghong和Shijie针对特定形式的三自由度关节空间机器人开发了一种分散自适应SMC,每个关节上都安装了控制力矩陀螺[262]。Arisoy和Bayrakceken展示了空间机器人高阶滑模控制的优点,将其应用于单连杆柔性漂浮机器人手臂[263],以利用SMC在无期望阻尼的弹性行为方面的鲁棒性。Guo和Chen开发了一种鲁棒末端滑模控制,可以同时控制航天器及其手臂末端执行器[164]。Lu等人利用终端SMC的概念进行开发:(i) 有一个翻滚目标的追踪飞船的姿态同步轨迹控制器[138];(ii) 近距离鲁棒最优姿态匹配控制[139];(iii) 直接对接目标[40]的耦合位置和方位控制。Saaj和Bandyopudhyay[157,166]开发了一种易于实现的滑模控制器,用于使用多速率输出样本的离散系统。他们证明了这种系统的切换函数和控制律可以直接从控制命令的输出样本中得到。
5.6 考虑到手臂的灵活性
使刚体多体系统的动力学模型更接近现实的一个步骤是考虑刚体[265]或关节的柔韧性。Spong[266]建立的具有柔性关节的机械臂动力学公式已被研究人员广泛应用[267]:
其中,K是关节的常对角刚度矩阵,![]() 为执行器轴对应的旋转角度矢量。输入命令向量
为执行器轴对应的旋转角度矢量。输入命令向量![]() 进入弹性关节的耦合动力学[267]:
进入弹性关节的耦合动力学[267]:
![]()
其中,![]() 由执行器的惯性组成。识别物体的弹性特性本身就是一项复杂的任务[268]。Kumar通过键合图模型控制了两自由度追逐臂系统的轨迹,该系统建模为两根欧拉伯努利梁[269]。Ulrich和Sasiadek[249]通过柔性系数的三阶多项式建模他们的柔性航天器手臂系统。他们还研究了四种控制方法处理柔性关节机器人手臂的能力[267]:(i) Slotine and Li (SLI)控制,由PD控制器和全动力学前馈补偿项组成[270];(ii) SLI的Spong展开,称为奇异摄动控制[271];(iii) Brogliato, Ortega and Lozano提出的非线性反步控制方法[272],(iv) PD控制。Murotsu研究了柔性对自由飞行系统控制的影响,并分类了几种路径规划方法,包括使用:(i) 当地的PD控制;(ii)一个虚拟刚性机械手;(iii) 伪加速度控制解决;(iv) 一个线性二次高斯(LQG)控制应用于手臂动力学的模态配方;(v) 复合伪分辨加速度控制;(vi) 使连杆处振动最小的模态控制[273]。Nanos综合了谐波齿轮机构的连杆柔度和关节弹性的影响,并在关节处引入了等效刚度[274]。Dubanchnet在他的博士论文中推导了柔性机械臂的动力学模型、路径规划和闭环控制方案,并通过硬件在环实验证明了他提出的方法的鲁棒性[275]。自适应和学习方案,如神经网络特别有利于控制具有柔性连杆机构的机器人,因为他们的复杂和往往不可预测的动态行为。Newton和Xu实现了一种递归神经网络结构来提高空间机械臂的控制性能,并将他们的结果与简单的PID控制器进行了比较[276]。
由执行器的惯性组成。识别物体的弹性特性本身就是一项复杂的任务[268]。Kumar通过键合图模型控制了两自由度追逐臂系统的轨迹,该系统建模为两根欧拉伯努利梁[269]。Ulrich和Sasiadek[249]通过柔性系数的三阶多项式建模他们的柔性航天器手臂系统。他们还研究了四种控制方法处理柔性关节机器人手臂的能力[267]:(i) Slotine and Li (SLI)控制,由PD控制器和全动力学前馈补偿项组成[270];(ii) SLI的Spong展开,称为奇异摄动控制[271];(iii) Brogliato, Ortega and Lozano提出的非线性反步控制方法[272],(iv) PD控制。Murotsu研究了柔性对自由飞行系统控制的影响,并分类了几种路径规划方法,包括使用:(i) 当地的PD控制;(ii)一个虚拟刚性机械手;(iii) 伪加速度控制解决;(iv) 一个线性二次高斯(LQG)控制应用于手臂动力学的模态配方;(v) 复合伪分辨加速度控制;(vi) 使连杆处振动最小的模态控制[273]。Nanos综合了谐波齿轮机构的连杆柔度和关节弹性的影响,并在关节处引入了等效刚度[274]。Dubanchnet在他的博士论文中推导了柔性机械臂的动力学模型、路径规划和闭环控制方案,并通过硬件在环实验证明了他提出的方法的鲁棒性[275]。自适应和学习方案,如神经网络特别有利于控制具有柔性连杆机构的机器人,因为他们的复杂和往往不可预测的动态行为。Newton和Xu实现了一种递归神经网络结构来提高空间机械臂的控制性能,并将他们的结果与简单的PID控制器进行了比较[276]。
5.7 鲁棒控制
在轨道上控制航天器手臂系统时,抗内外扰动的鲁棒性是至关重要的,因为轻微的偏差可能损坏系统或目标,在剧烈的情况下可能导致碰撞和产生碎片[277]。虽然机械手路径规划的鲁棒性在文献中是一个反复出现的目标,但直接鲁棒控制器并不常用。Aghili和Su通过使用激光扫描仪和IMU,应用ICP和AKF算法设计了一个鲁棒的相对导航系统,该系统被证明对恶劣的光照条件[59]具有鲁棒性。Dor和Tsiotras研究了ORB-SLAM在非合作交会问题中的应用,证明了其对航天器旋转扰动扰动位姿估计的鲁棒性[278]。许多滑模和自适应控制器也展示了抗干扰能力[139,279]。鲁棒控制方案通常是最优控制的一种形式,其目标函数代表了干扰和不确定性对输出的影响。非线![]() 和
和![]() 控制器的鲁棒性是众所周知的对内部和外部干扰的健壮[143]。
控制器的鲁棒性是众所周知的对内部和外部干扰的健壮[143]。![]() 控制器是由Johansson在1994年开发的基于二次优化运动控制[280]及其改进版拒绝干扰则由chen等人提出[165]。该方法在一个固定底座的机器人手臂上进行了测试[165],并用于空天和航天器的姿态控制,因为它们面临相当大的外部扰动[281,282]。
控制器是由Johansson在1994年开发的基于二次优化运动控制[280]及其改进版拒绝干扰则由chen等人提出[165]。该方法在一个固定底座的机器人手臂上进行了测试[165],并用于空天和航天器的姿态控制,因为它们面临相当大的外部扰动[281,282]。![]() 是一种最佳的控制方案,控制器设计的无穷范数限制干扰对系统输出的影响。最近已经尝试使用
是一种最佳的控制方案,控制器设计的无穷范数限制干扰对系统输出的影响。最近已经尝试使用![]() 和
和![]() 方法组合来控制柔性关节机械手[283],以防止执行器饱和。Saaj和Seddaoui进行的仿真验证了基于非线性
方法组合来控制柔性关节机械手[283],以防止执行器饱和。Saaj和Seddaoui进行的仿真验证了基于非线性![]() 方案的前馈\反馈联合补偿的手臂和航天器基座并行控制的鲁棒性和稳定性[264]。他们还展示了在OOS任务中线性控制器的能力,如PID、前馈和LQR方法[284]。图11显示了它们的控制架构。
方案的前馈\反馈联合补偿的手臂和航天器基座并行控制的鲁棒性和稳定性[264]。他们还展示了在OOS任务中线性控制器的能力,如PID、前馈和LQR方法[284]。图11显示了它们的控制架构。
在最近的一项研究中,他们也提出了一个健壮的![]() 控制律补偿扰动效应在空间机械臂操作,其存在内部动态耦合,质量变化,外部干扰[143]:
控制律补偿扰动效应在空间机械臂操作,其存在内部动态耦合,质量变化,外部干扰[143]:
其中,B是一个输入矩阵,R和![]() 为优化过程中满足Riccati方程的调优矩阵。像之前一样,
为优化过程中满足Riccati方程的调优矩阵。像之前一样,![]() 分别为基体和机械手的跟踪误差。
分别为基体和机械手的跟踪误差。
其中,K和Q都是权重函数,![]() 为衰减水平,这是由Cholesky因子分解得到的对R的约束[143]。
为衰减水平,这是由Cholesky因子分解得到的对R的约束[143]。
Siquera并发控制器的鲁棒性进行了比较研究使用![]() 和
和![]() 方案,他们的组合,
方案,他们的组合,![]() -综合的方法应用于驱动系统[285]。这一比较证明
-综合的方法应用于驱动系统[285]。这一比较证明![]() -综合是最健壮的方法,同时也是计算代价最高的方法,而
-综合是最健壮的方法,同时也是计算代价最高的方法,而![]() 是最不健壮的控制方法。
是最不健壮的控制方法。![]() 控制的另一个鲁棒性能演示是由Lee和Mavroidis,他们通过LQR方法合成了
控制的另一个鲁棒性能演示是由Lee和Mavroidis,他们通过LQR方法合成了![]() 控制,以拒绝处理柔性载荷引起的扰动[286]。Dabuchnet等人利用PD控制器实现了一个固定的
控制,以拒绝处理柔性载荷引起的扰动[286]。Dabuchnet等人利用PD控制器实现了一个固定的![]() 逻辑,用于在跟踪目标上的抓住点时拒绝干扰[287]。
逻辑,用于在跟踪目标上的抓住点时拒绝干扰[287]。
6. GNC的抓取和抓取后
当末端执行器撞击目标时,手臂将经历一个重要的反作用力,该反作用力也被转移到追踪航天器上。这种反应的不良影响应尽量减少或控制。除捕获后阶段外,追击器与目标作为统一的动力对象,其惯性等动力参数的确定是必需的。机动应计划好调整目标的方向、扭转目标、移动目标或减轻目标的影响。如果目标是非合作的,通常的第一步是阻尼目标的运动,以稳定系统的轨迹和避免任何碰撞。
6.1 捕获阶段的GNC注意事项
在处理冲击时的反作用力有两种常见的方法:(i) 通过力控制方法或结构阻尼来吸收冲击;(ii) 通过适当选择接触点和精心设计的预冲击轨迹来最小化冲击力。Yoshida等人提出的阻抗控制就是前者方法的一个例子,该方法用于捕获和控制非控制目标的动力学[106]。它结合了一个分析质量-弹簧-阻尼模型,使冲击力最小化,并提供了一个保持接触或将目标推开的标准[106]。Yoshida等人利用虚拟的质量和接触点的弹簧,制定了两个自由漂浮体之间的接触动力学[90]。弹簧常数(阻抗)是机械臂结构的一个函数,它将被调整以在接触点引入所需的阻抗。可以规划预冲击配置,使冲击不会改变机器人的角动量[200]。Nenchev和Yoshida研究了将最小冲击动量传递到基体的冲力方向[200]。他们扩展了这些发现,并使用RNS来促进捕获后机动中的手臂控制[288]。Cheng、Tianxi和Yang引入了一种基于动态抓取面积概念的抓取策略,研究了抓取控制参数和质量分布的影响[105]。通过实验,他们表明,通过仔细调整控制参数,同时考虑手臂的冲击速度,可以显著降低反作用力。由于手臂的弹性自由度受到冲击,因此在捕捉瞬间连杆的弹性特性变得至关重要。Liu, Wu和Lu研究了两种柔性臂在捕获后的控制和不控制情况下的弹性行为[104]。
6.2 捕获后系统辨识
当操纵非合作目标时,在线参数识别是至关重要的,因为:(i) 目标的准确动态特性事先不知道;(ii) 撞击可能导致目标变形;(iii) 捕获后跟踪器和目标的运动是耦合的。识别程序通常基于追逐器的运动或末端执行器和目标之间的扭矩\力。目标模型的不准确性往往导致捕获后立即出现意外的翻滚运动,导致控制器性能不佳。在线自适应技术已被提出,以减少这些不准确性的影响。Abiko利用自适应控制律中力和动量之间的耦合,将目标的运动转移到追逐器上的动量轮上[121]。Murotsu等人提出了另一种方法,在只驱动机械臂的一个关节时,利用动量守恒来识别追逐器-臂-目标这系统的耦合动力学和惯性张量[117]。将系统划分为三个刚体,通过将追击臂-目标的总线动量和角动量设为零,形成目标惯性参数(10个变量)与目标线速度和捕获前追击臂角动量可测参数(6个变量)之间的(线性)关系。通常,用于识别的基本方程是静不定的,需要多个数据集或多个手臂连接的移动来执行识别。Murotsu在同一研究方向上讨论了另一种方法,包括使用牛顿-欧拉方程来估计系统参数[117]。Rackl提出了一种基于力矩的抓后识别方法,该方法不需要知道基本加速度[122]。Nguyen和Sharf提出了一个临时识别逻辑和一个自适应无反应控制器,以最小化捕获和捕获后识别之间的过渡过程中不确定性的不利影响[123](见图12)。
6.3 捕获后控制
捕获阶段对整个跟踪目标系统的动力学特性有一定的影响。Cyril等人通过使用撞击模型来识别两个物体的广义速度的变化,制定了捕获前后的整体系统动力学[116]。他们还研究了手臂灵活性对冲击平滑度、捕获后动力学和控制性能的影响程度[115]。许多捕获前方法适用于捕获后控制。具体来说,自适应控制律可以通过纠正目标模型估计中的不确定性而具有优势[289]。例如,Nenchev和Yoshida提出了预捕获中用于干扰最小化的相同反应零空间概念来分析冲击的动力学[61]。Yoshida和Dimitrov提出了关节空间的正交分解来分析捕获后的行为,将不需要的目标运动转移到跟踪器的AOCS中,并执行捕获后的运动规划[113]。他们还提出了在空间机器人系统中预加载偏动量的概念,以增强捕获和捕获后行为[113]。在失去推进器或执行器的情况下使用的可重构控制逻辑,在机器人系统与未知目标统一后,也能够在模型不确定性的情况下提供全局渐近稳定性[178]。 Nishida和Yoshikawa开发了一种联合虚拟深度控制方法来制动目标并减轻追逐器的冲击负荷[290]。他们还提出了一种联合顺应性控制,并在末端执行器中添加缓冲,以减少冲击带来的不良影响[291]。Sharf等人开发了两种固化技术来重新分配捕获后翻滚目标的动量:比例积分控制和冗余分辨率控制[114]。
6.4 阻抗控制
当涉及接触时,利用基于力的控制方案代替基于状态的控制器是特别有益的。这些方法包括阻抗控制、导纳控制或顺应控制。控制中的顺应性在这一步骤中是至关重要的,因为大的力量可以破坏缓解过程。因此,Hirano、Kato和Saito提出了一种基于顺应控制的在线鲁棒路径规划算法,用于特别处理大型翻滚目标[292]。阻抗控制是一种常用的方法来抑制非合作目标的不希望的运动[293]。它包括在关节处增加弹簧和阻尼器等动力元件来控制臂所遇到的力[110](见图13)。
接触通常被建模为其自身的阻抗。Uyama, Yoshida, Nakanishi和Nakaoga提出了一种基于阻抗的接触控制算法,该算法调整阻抗参数以获得理想的阻尼和恢复系数(航天器和目标的最终相对速度与初始相对速度的比值)[294]。阻抗控制律定义为
![]()
其中,![]() 为接触力,M\C和K是阻抗控制的质量系数,阻尼系数和刚度系数,
为接触力,M\C和K是阻抗控制的质量系数,阻尼系数和刚度系数,![]() 和
和![]() 是末端执行器和目标上抓取点相对于轨道惯性坐标系的位置,并在轨道惯性坐标系表示。通过Palma和Seweryn进行的新模拟,已经证明了柔度控制处理接触动力学的实际优势[295]。Moosavian、Rastegari和Papadopoulos也研究过使用多臂阻抗控制来控制单个目标。
是末端执行器和目标上抓取点相对于轨道惯性坐标系的位置,并在轨道惯性坐标系表示。通过Palma和Seweryn进行的新模拟,已经证明了柔度控制处理接触动力学的实际优势[295]。Moosavian、Rastegari和Papadopoulos也研究过使用多臂阻抗控制来控制单个目标。
6.5 目标的灵活性
不仅追逐者-机械臂系统的结构柔性,目标对象的结构柔性也影响着追逐者-目标的系统的整体动力学,这在捕获时刻和捕获后机动中都是至关重要的。Ishijima等人[163]研究了使用自由飞行操纵柔性空间结构,采用模态主动阻尼控制律抑制不必要的振动,并通过追尾推进器操纵有效载荷,类似于刚体。空间机械臂处理柔性目标的另一个例子发生在装配任务中。Boning和Dubowsky提出由一组空间机器人在轨道上组装大型空间结构[297]。这使得机器人团队的动力学建模和协同控制变得非常复杂,因为在装配过程中会激发各种结构的柔性模态。Gasparri和Pisculli提出了当空间机器人配备两个柔性臂与柔性目标交互时,捕获和捕获后阶段的两种最优柔性补偿方法[120]。
6.6 最优控制
与捕捉前阶段相似,捕捉后运动规划中也可能存在一定的优化条件。在这种情况下,目标动力学通常被描述为自由浮动刚体动力学(欧拉方程)[119]。目标通常是使目标卫星静止,并考虑扭矩限制![]() ,在最短时间内将其移动到特定位置。正如Aghili所建议的那样,下面的为反翻滚机动的成本函数应该被最小化[118,119]
,在最短时间内将其移动到特定位置。正如Aghili所建议的那样,下面的为反翻滚机动的成本函数应该被最小化[118,119]
受下列条件限制:![]() 。然后最优控制理论规定时间最优转矩(
。然后最优控制理论规定时间最优转矩(![]() )为:
)为:
其中,![]() 满足:
满足:
他们最近将捕获前最优控制方法进一步扩展到捕获后翻滚目标的应用[298]。Wang等[112]也提出了一种基于二次Bezier曲线和自适应粒子群优化算法的最优解离被捕获目标的策略。
7. GNC技术的展望
在本节中,基于强化学习和几何力学的两类新兴控制方法进行了研究,并简要探讨了它们在空间机器人系统GNC中的应用。在后续小节中强调了每种方法在增强现有GNC系统或解决其缺点方面的能力。
7.1 强化学习
长期的自主要求在为空间机器人设计的GNC技术中纳入机器智能,以适应其物理组件、环境或任务要求的变化[299]。人工智能(AI)为GNC设计提供了另一种方法,包括基于目标的规划、自我\环境感知、学习\训练、推理、模式识别和适应性任务执行[300]。融合人工智能和机器人的主要目标之一是通过学习来优化自主水平,学习提供了预测未来的能力,无论是在规划任务还是与周围环境的互动中。机器学习(ML)是目前人工智能和自主研发的核心。机器学习的三种主流,即有监督、无监督和强化学习,最后一种是最适合GNC应用的。强化学习(RL)通常用于机器人自适应控制律,以拒绝建模缺陷或干扰。RL被纳入各种控制方案,包括自适应、鲁棒或简单PID,以提高地面机器人手臂的轨迹规划和控制性能[301 303]。最初,对自然界中最佳行为的观察激发了对RL的研究,作为一种从环境交互作用中学习的计算手段。这些互动包括从奖励或惩罚的角度评估所采取行动的质量。RL技术可以在策略之外工作,并开发自己的系统\环境模型[304],这使得它们在处理未知或变化环境、缺乏全面的自我模型或面临大量内部或外部干扰的系统中具有吸引力。最近,一个完全在虚拟环境中训练的基于RL控制逻辑的机器人成功迁移到物理世界[305]。在虚拟环境中进行训练不仅可以更快、更安全,而且可以使控制策略对系统辨识中的建模误差和不确定性具有更大的弹性[306]。基于模型的RL包括对建模偏差敏感的规划[307]。RL也可以改善非线性系统的闭环控制性能,正如Bhasin在他的论文[308]中所研究的那样。他开发了一个鲁棒自适应控制器与动作评价架构,可以处理干扰。Senda等人通过RL改进了空间机器人模拟器的在线性能和计算效率[309]。考虑到许多OOS任务对自主性的需求和非合作目标的未知性质,RL可以显著提高现有控制方案的性能,以改善轨道服务航天器的GNC。现有的RL算法还没有准备好在空间系统中实际实现[310]。尽管空间系统的资源有限,但无模型的RL方法需要大量的探索性试验来找到最优策略。此外,当前的RL算法通常在低维动力学系统中工作得更好,如果不仔细调整,它们可能会将机器人系统推入不稳定区域或不安全接触[310]。因此,一种实用的学习方法必须建立在能够捕获空间机器人系统的模块化、约束、环境相互作用和非线性的模型的基础上。虽然学习在硬件与真实环境交互时提供了最好的结果,但出于安全原因,学习过程还应该涉及一些仿真方面[311],以避免对机器人和我们在轨道上的资产造成灾难性的伤害。表2总结了强化学习为在轨机器人任务的不同阶段开发先进GNC技术提供的可用工具。
| GNC方法 | 潜在应用 | 优点 | 缺点 |
| Q-Learning | -识别轨道扰动; -识别不确定空间机械臂预捕获; -捕获后阶段识别目标; |
-作为其他RL方法的基础; -实时识别不确定系统; -拒绝噪音和干扰; -实现机器人自我评估; |
-多次试验; -适用于离散系统模型; -可能导致不安全的系统配置; |
| 随机路线图 |
-无碰撞臂路径规划; -最小扰动臂路径规划; -并行航天器/机械臂路径规划; |
-计算效率高; -与离散学习方法和控制器兼容; -避免动态障碍物; -适应不断变化的环境; |
-产生次优轨迹; -生成不连续的命令; |
| 小脑模型算术计算机 | -类似于PRM方法 | -与离散学习方法和控制器兼容; -相对于连续和完整的网格算法,需要较少的探索; |
-粗略估计系统; -在环境的不同部分表现不均匀; -实时性能较慢; |
| 评价器 | -促进空间机械臂的增强自适应控制; -在捕获后阶段实时调整控制器; -实时识别目标; -拒绝手臂的GNC轨道干扰; |
-直接适用于连续空间机械臂控制; -实时适应和识别环境和不确定性; |
-计算密集; -需要复杂的硬件和测试; |
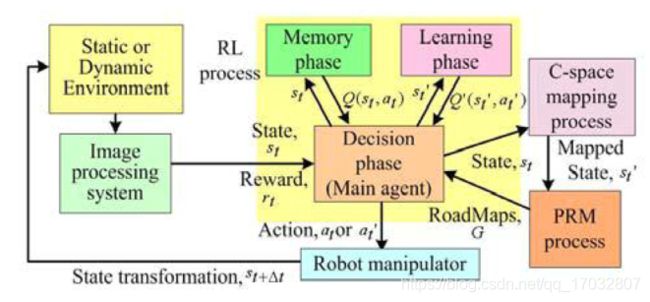
7.1.1 路径规划
虽然基于RL的控制器通常使用环境的离散模型,称为马尔可夫决策过程(MDP),但它们可以通过以下方式得到连续的问题:(i) 便于通过概率路线图(PRM)[312,313]或小脑模型算法计算机(CMAC)[314,315]离散化的机器人配置空间的路径规划;(ii) 行为-评价算法[316]。行为-评价方法将在第7.1.4节中进一步讨论。臂的构型空间被表示为笛卡尔空间,例如,图14中有两个关节的平面固定基臂是二维笛卡尔空间。在周围环境中观察到的障碍物可以映射到构形空间[312]。如果这个映射是完整的,RL可以为任何期望的起点和终点生成无碰撞的路径[317]。
如前所述,RL可以与其他路径规划方法融合,如PRM[313](图15)。
在预处理阶段,PRM在配置空间的允许区域中生成一组随机点,这些点被称为节点或里程表。在查询阶段,这些节点通过腿连接起来形成一个网格,称为路线图(RM),机器人可以在其中导航而不碰撞障碍物。图14描绘了映射到其构型空间的2-DoF固定基臂的工作空间。然后将构型空间离散化,生成的节点形成RM。然后在该RM中生成一个全局半最优路径[312]。该方法生成的路径可能不是全局最优路径,但它是一个很好的近似,有利于减少计算量。结果表明,该方法适用于GNC系统的实时应用。学习或优化算法,如RL[312]和Q-learning[318],通常与PRM[315,319]相结合。RL过程中的一个智能体在一个价值为![]() 的确定状态
的确定状态![]() 选择一个行动
选择一个行动![]() 与行为价值
与行为价值![]() 的概率
的概率![]() 就引出了下一个状态
就引出了下一个状态![]() 。它从目标状态和动作中观察奖励
。它从目标状态和动作中观察奖励![]() ,并在环境中重复相同的过程。经过几个周期从开始到终端状态和更新的值根据观察到的奖励,该算法收敛于最优策略
,并在环境中重复相同的过程。经过几个周期从开始到终端状态和更新的值根据观察到的奖励,该算法收敛于最优策略![]() 以通过环境指导系统。状态s是手臂的某种配置,其状态值为V。函数V通过动作值Q的预期值更新,该值用于在状态s中执行的不同操作,策略为
以通过环境指导系统。状态s是手臂的某种配置,其状态值为V。函数V通过动作值Q的预期值更新,该值用于在状态s中执行的不同操作,策略为![]() 。然后,通过在特定状态s下选择某个动作a[320],通过期望返回的和来更新函数。
。然后,通过在特定状态s下选择某个动作a[320],通过期望返回的和来更新函数。
![]()
![]()
其中,![]() (返回)表示步骤t后按照
(返回)表示步骤t后按照![]() 政策累计奖励。不同的RL算法对V、Q使用不同的更新规则和各自的学习方法。Park等人研究了不同的RL方法,如Monte-Carlo、Q-learning、simple Temporal Difference (TD)和Dynamic Programming (DP),用于手臂路径规划,并建议Q-learning在网格勘探和开发中的平衡行为[312]。它们结合图像处理来观察变化的环境、障碍物和工作空间,形成一个PRM。Q-learning agent在PRM中控制手臂的运动,评估其状态,学习并更新控制逻辑。Q-learning在学习阶段使用以下公式更新其行动价值。
政策累计奖励。不同的RL算法对V、Q使用不同的更新规则和各自的学习方法。Park等人研究了不同的RL方法,如Monte-Carlo、Q-learning、simple Temporal Difference (TD)和Dynamic Programming (DP),用于手臂路径规划,并建议Q-learning在网格勘探和开发中的平衡行为[312]。它们结合图像处理来观察变化的环境、障碍物和工作空间,形成一个PRM。Q-learning agent在PRM中控制手臂的运动,评估其状态,学习并更新控制逻辑。Q-learning在学习阶段使用以下公式更新其行动价值。
![]()
其中下标t为时间步t的参数,![]() 为折现因子,定义算法展望未来的程度,
为折现因子,定义算法展望未来的程度,![]() 为学习率。通常,Q-learning代理会根据-贪婪策略移动,但会根据每个节点上的实际最佳路径(贪婪解决方案)更新Q,在大多数情况下遵循最优路径(利用)的同时确保对环境的探索。在-贪婪策略中,智能体以(1−)×100%的次数遵循最优路径,以×100%的次数随机探索环境。
为学习率。通常,Q-learning代理会根据-贪婪策略移动,但会根据每个节点上的实际最佳路径(贪婪解决方案)更新Q,在大多数情况下遵循最优路径(利用)的同时确保对环境的探索。在-贪婪策略中,智能体以(1−)×100%的次数遵循最优路径,以×100%的次数随机探索环境。
7.1.2 系统和环境识别
强化学习算法可以生成MDP或连续模型来捕获系统或环境的行为。即使是离线方法(不是实时的),如蒙特卡罗,也可以合并数据集聚合(DAgger)算法来识别周围环境[321,322]。不完全可观测的环境也可以通过部分可观测的Markov决策过程来估计,这证明了通过在线自适应控制可以实现最优行为[323]。与模型预测控制相比,RL在不需要预先确定模型的在线系统估计中显示了强大的性能[301]。Hwang, Tan和Tsai证明了RL可以捕获环境中的非线性,并通过构建和调整神经网络有效地将其线性化[324]。他们还证明了该方法的系统模型独立性和在控制系统时进行估计的能力[324]。Fisac等人在在线学习逻辑中加入了对环境的离线粗略估计,以确保算法在学习系统时的安全性[325]。基于模型的识别技术包括由RL匹配和调整的预定义模型,以表示环境。Ross和Bagnel开发并实现了一种使用基于在线模型的RL的系统辨识方法,以实现对未知环境的接近最优控制策略[322]。Pane提供了另一种使用RL和动作-评价逻辑的在线系统识别方法,用于物理特性随时间不可预测地变化的机器人[326]。基于RL的控制器可以同时识别系统模型,间接控制它,适应系统\环境的变化,优化成本函数[323]。目标识别是在轨机器人任务的另一个阶段,可以从RL方法中显著获益[317]。
7.1.3 移动机器人的应用
RL和动作-评价学习算法,由于能够排除建模缺陷、噪声和外部干扰,在移动机器人系统的自治应用中表现出了潜力[327,328]。这已经通过模拟和真实实验得到了证实[329]。Ostefaw等人利用受扰动漫游者穿越路径的记录信息,生成了基于学习的非线性模型预测控制律[303,330]。Mihelich利用RL参与者来评估不均匀的环境,通过从预定义集中选择增益来调整腿式机器人的鲁棒控制器[331]。Bernstein等人利用任务空间的可分解性,将任务空间分解为弱耦合的独立环境模型,提高了自主行星漫游者控制器的实时决策性能[332]。基于学习的车辆控制器已经证明了能够自主地考虑外部干扰、输入非线性和模型不确定性[333]。
7.1.4 机器人自评估与自适应控制
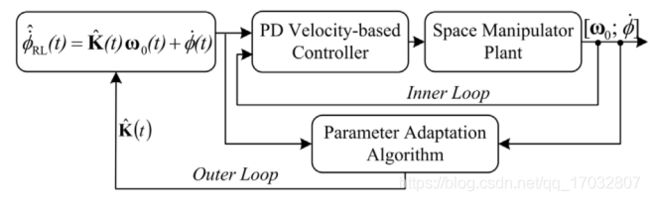
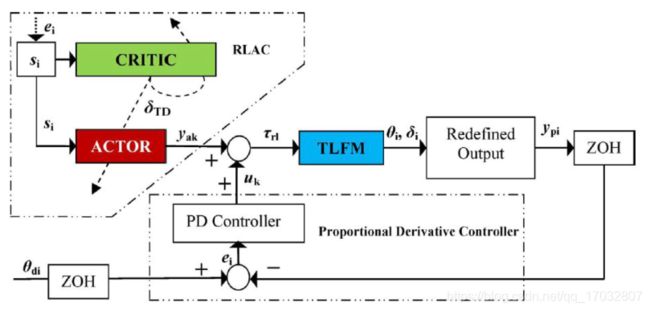
基于时间差异的方法可以被认为是评估其环境模型并更新其估计的诊断方法,与蒙特卡罗方法相反,蒙特卡罗方法需要等待一个完整的事件完成来更新他们的模型。动作-评价控制器可以使用关联搜索网络(ASN)来评估他们对机器人动力学的理解[334],确保对建模误差的鲁棒性。Eski等人通过实验研究了人工神经网络分析机械臂操作故障的能力[335]。动作-评价逻辑可以增强另一个控制器,以评估其性能并在整个操作过程中对其进行调优。Pradhan和Subudhi开发了一种用于柔性手臂的自适应控制器,并对其性能进行了评估[336]。他们控制一个非最小相位,欠驱动的可变有效载荷系统。行动者批评逻辑和最小二乘适性跟踪自适应记忆方法可以通过跟踪错误的来源并将不希望的动态行为与其原因联系起来,从而促进自我评估过程[336]。
图16显示了如何在PD控制器上添加一个动作-评价以适应双连杆柔性机械臂的动态变化[336]。动态输出被更新,并通过一个零阶保持器以兼容在线连接到控制器。控制器的动作-评价部分能够使时域差分误差![]() 最小化
最小化
![]()
这是一个预测错误。这里,向量![]() 是智能体回归量,W是智能体的矩阵控制器权值[336]。自适应神经控制是另一种适用于空间机械臂的基于人工智能的RL控制器。控制动作可以由神经网络产生,模型的精度可以由一个评价器来评估,这可以捕获非线性效应[337]。
是智能体回归量,W是智能体的矩阵控制器权值[336]。自适应神经控制是另一种适用于空间机械臂的基于人工智能的RL控制器。控制动作可以由神经网络产生,模型的精度可以由一个评价器来评估,这可以捕获非线性效应[337]。
Macnab和D Eleuterio在自适应控制器中加入了人工神经网络和CMAC,通过在线更新控制逻辑中的权值来提高性能,同时保持稳定性[338]。Lin针对不确定模型的机器人采用了另一种RL自适应控制器,其中包括一个智能体来收集固定增益控制器的信号,一个评估控制器的自适应评价器和一个模糊动作产生元件[339]。采用RL的机械手的自适应控制器也能够直接识别有效载荷的变化,并相应地调整控制器[340]。该概念可用于类似的空间机械臂,并评估控制器模型中的误差。
7.2 几何力学与控制
几何力学是应用数学的一个分支,研究非线性动力系统在其构形流形上的有可能也可能不表现出李群结构。该方法扩展了微分几何中的工具,以一种无坐标的方式处理这样的复杂系统。位形流形Q包括系统的所有可能的位形,相空间由表达动力学所需的状态组成。例如,拉格朗日系统可以用其构型和速度,切丛的元素TQ,根据构型及其共轭动量定义了哈密顿方程,余切丛T*Q等方式来描述。因此,正则系统的动力学是相空间上的向量场,其积分曲线代表了系统的时间演化[341]。对于刚性航天器机械手系统,系统的位形流形是n+6维度的,它对构成该系统的刚体之间所有允许的相对变换的集合是微分同态的,该系统具有李群结构。。
由Marsden和Wein- stein[342]和K. Meyer[343]提出的减少非线性系统相空间及其相关动力学的思想是几何力学的核心。还原可以通过克服欠驱动[344]、处理非完整性[345]、启用并发控制、允许控制律之间切换[346]来改进GNC方法,这些在空间机械臂的GNC中都是至关重要的。特别是在接近操作中,这些自由浮动系统是欠驱动和非完整的,因为存在一个非驱动的基础导致动量守恒。他们必须同时控制末端执行器和基地,以重新建立遥测链路完成任务执行。由于在轨空间机器人的操作包含几个阶段,它们可以从平滑切换控制策略中获益[347]。研究人员已经能够通过利用机器人[348 350]、车辆[351]、机械手[352]、无人机[353]和多体系统[341]的几何特性,证明上述优点适用于现实生活中的机械系统。Müller和Terze提供了几何建模和控制在多体系统中的潜在应用的广泛概述[341]。表3总结了几何力学提供的方法,这些方法有助于为在轨机器人任务的不同阶段发展先进的GNC技术。
| GNC方法 | 潜在应用 | 优点 | 缺点 |
| 动力学还原 | -包括自由浮动状态下的非零动量; -在预捕获阶段生成并行机械手/基本运动的轨迹; -利用捕获后阶段的重建方程设计适应规律; -在减少相空间中执行部分反馈线性化; |
-消除对航天器非驱动自由度的依赖; -处理空间机械臂运动的非完整控制问题;-提供鲁棒的感官噪音在减少航天器的自由度; -提供准确的分析平台; |
-具有挑战性的实现; -易于建模的不确定性,由于减少动力学的复杂性; -不适用于外部干扰系统和自由飞行; |
| 优化控制 | -捕获前阶段的非完整路径规划和最优控制; -为姿态同步阶段提供最优制导律; -提供最佳的轨道环境接近; |
-严格执行变异演算,产生创新的解决方案; -处理空间机器人的非完整和欠驱动性质; |
-具有挑战性的实施; -对系统/目标不确定性或轨道干扰不够稳健; -数值上繁琐; |
| 几何部分反馈线性化 | -在捕获前阶段同时控制基座和末端执行器; -研究预捕获阶段零动态和相对稳定性; |
-提供奇点分析工具; -处理非完整和欠驱动系统; -处理流形上的输出; |
-具有挑战性的实施; -需要精确的系统模型; |
| 几何鲁棒自适应控制 | -在预捕获阶段手臂末端执行器控制中拒绝外部干扰; -捕获后阶段识别目标并提供全局自适应控制律; |
-通过流形上的积分提高数值稳定性; -去除不必要的奇异点由于参数化; |
-具有挑战性的实现; -瞬态太慢; |
7.2.1 对称性和动力学还原
几何物体的对称群是物体保持不变的所有变换的群[354]。动力系统,对称性的作用被定义为一个李群G系统的相空间,使动态向量场不变的。如果系统受到约束,李群作用也将保持系统的约束。基于Noether定理,Hamilton原理中的作用泛函的任何连续对称性都对应于沿系统轨迹的一个守恒量,称为动量映射[355]。在对称性存在的情况下,通过对对称群进行商运算,可以使用微分几何技术将系统的运动方程正式投影到其相空间的子流形上[356]。例如,通过将多体系统的相空间缩小为系统形状空间的余切丛,可以消除多体系统由于动量守恒(不一定为零)而产生的琐碎行为。对称约简过程可以分为三个步骤:(i) 将动力学限制到相空间的一个受约束的子流形;(ii) 用群作用对受约束的子流形进行商运算;(iii)用余切集识别商流形[358]。这种方法在非完整约束和无约束力学系统中是常见的。
辛约简定理[342]对Hamiltonian和Lagrangian系统的多种约简方法的统一产生了历史性的影响,如经典的Routh方法和拉格朗日系统的循环参数约简[359,360]。利用余切丛的辛结构和泊松结构,已经发展了许多约简理论,如[361 363]中报道的哈密顿系统的约简理论和[364 366]中报道的拉格朗日系统的约简理论。对于具有非完整约束的系统,其动力学是通过Lagrange-d’Alembert方程或Hamilton-d‘Alembert方程来表述的,用对称性进行简化可以追溯到Chaplygin[367]的工作。他消除了Lagrange-d’Alembert方程中的Lagrange乘子,用系统的循环参数表示了一个简化相空间中的非完整系统。他的结果被Koiler推广到包括还原过程中的非交换群行为[368]。对于具有对称性的非完整系统的其他约化理论,已用哈密顿或拉格朗日形式进行过报道。在[345]中引入了一种以定义非完整连接和非完整动量图为中心的简化方法。由van der Schaft和Maschke[369]的一篇论文演变而来的[362]也解释了使用泊松几何的类似方法。具有对称性的非完整系统的其他简化形式可以追溯到Bates和Śniatycki[370]、gaybalmaz和Yoshimura[371]以及Ohsawa等人[372]的著作中。Chhabra等人讨论了一个几何方法来简化具有多个非完整关节的多体系统的Hamilton-d’Alembert方程[357]。他们还提出了一类具有仿射非完整约束的对称力学系统的动力学约简的几何方法[358]。他们的方法统一了现有的Chaplygin系统(气体模型)和对称动量守恒哈密顿系统的约简程序,它们通常有不同的约简程序。
动态系统的简化对于研究系统的固有行为以及设计GNC系统是很有帮助的。Sreenath提出了保持角动量的控制律,利用系统动力学的辛约简[373]。他在此基础上进一步发展了反馈控制律,用于基体再定位[374]。Chen在Sreenath研究零动量空间开链多体系统的基础上,提出了一种基于多周期关节运动路径规划方法的非光滑控制反馈律[375]。Koon在他的博士论文中执行了Lagrangian约简来提出最优控制律,并将这种约简方法与其辛(哈密顿)对应物进行了比较[376]。Shen、Schneider和Bloch在多体系统的形状空间中引入了一种非线性路径规划和控制方法,该方法通过减少零角动量下的动力学来实现[377]。他们通过形状变化规划系统轨迹,分析其可控性[378,379],并进一步开发其在非完整系统中实现的控制器[380]。相空间的动态缩减允许机器人通过利用对称性产生精确的可行运动来产生激进和快速的运动[381]。四旋翼无人机、潜水器和其他类型的机器人也受益于具有执行侵略性机动的能力[344]。Huang提出了一种非线性控制算法,利用SO(3)的几何特性作为无人机的位形流形,设计了一个能够执行侵略性机动、抑制干扰、快速纠正误差和精确定位的控制器[353]。Cortes等人从仿射连接控制系统的角度研究了具有对称性和非完整约束的欠驱动机械系统的控制[382]。
通过对称性进行动态简化的一个好处是降低了计算负担,从而允许具有较低计算能力的设备来控制系统。Avizzano为Clavel delta并联机器人开发了一种控制方法,采用了一系列几何简化,以减少数学上复杂问题的计算负荷[348]。模型预测和基于RL的控制器也可以受益于减少过程的较低的计算负担。以李群SO(3)为模型的刚体姿态可以通过模型预测控制具有较高的计算效率,避免欧拉角奇异,优化能量消耗和拒绝扰动[383]。
除对称约简外,常用的约简方法还有截断法、约基法、适当正交分解等。虽然这些方法限制了模型的精度,但它们允许研究人员在更小的空间中提出GNC方法。
7.2.2 几何路径规划
无论是一个复杂的航天器-机械臂系统、还是一个轮式移动机器人或任何其他形式的具有对称和非完整约束的动力系统,路径规划者可以受益于几何力学提供的改进性能或新的控制能力。Hussein和Bloch利用仿射连接理论、导航函数方法和拉格朗日乘子法来规划一类具有非完整约束的欠驱动系统的次最优轨迹以避免障碍物[384]。他们还研究了有限时间内具有位形流形SE(3)的刚体群的约束最优轨迹跟踪[385]。Shammas等人分析并生成了混合机械系统的步态,该系统的运动同时受一组非完整约束和一个守恒的广义动量控制。通过适当地求助于几何力学,他们能够表明所得到的运动有两个部分:几何贡献和动态贡献[386,387]。最近,基于运动学习策略的智能和高效的自主导航技术已经被引入用于车辆控制目的的深度学习[388],并在室内运动控制和避障方面表现出良好的性能。
7.2.3 线型控制
几何工具可用于闭环控制[389]以提高效率,提高控制逻辑处理欠驱动系统的能力[217],有助于统一完整约束和非完整约束[362],并为空间机械臂等复杂系统引入新的控制算法[390]。许多机器人系统是欠驱动的,控制输入通常通过机器人的内部自由度进行。尽管这些系统控制起来相对复杂,但可以提出几何技术来保证它们在某些流形上的可控性[391]。一个不受AOCS系统主动控制的自由漂浮空间机器人是一个欠驱动系统。Chen和Mukherjee证明,对于零动量系统,如果机械手中的非驱动关节有制动器,那么整个系统可以在收敛到期望终点的同时完全停止[217]。同时,如果驱动自由度超过非驱动自由度,且两组状态之间存在强耦合,则系统可以稳定在任何期望的配置,而无需航天器驱动。Viswanathan针对几个欠驱动动力系统[344]提出了一种集成GNC逻辑,这些系统以SE(3)为模型,采用离散Lagrange-d’Alembert方程以李群变分积分器的形式建模。将该方法应用于欠驱动无人机的实际应用中。欠驱动无人机器人系统,如轮式车辆,可以利用控制拉格朗日系统的几何控制技术[392],利用李群指数坐标,并在减少的相空间中使用对数反馈,实现自平衡能力。柔性系统本身也是欠驱动的,可以受益于几何控制律。Taha[351]研究了具有2个作动器的欠驱动3自由度扑动板的控制问题,结合几何控制和平均理论稳定系统。
7.2.4 非完整力学和控制
由于自由浮动机械臂动力学方程的动量守恒,产生了非完整约束。Boltzmann Hamel方程是在李群上推导这种系统模型的一个样本方法[393]。它在准坐标中描述了系统的动力学,因此能够包括所有完整和非完整关节[394]。Duindam和Stramigioli推导了全局位形流形上的非完整多体系统的这些方程,而不是其局部坐标[395]。因此,它们能够避免控制设计中由于坐标分配而产生的不真实奇异,并生成具有一般完整或非完整关节的多体系统的方程组。Hussein和Bloch论证了在非完整系统的最优控制中使用仿射连接公式的优点[384]。它们最小化了欠驱动、非完整轮式机器人的控制输入。他们没有把系统的对称性纳入他们的公式中。olfatis-saber在他的博士论文中探讨了具有对称性的欠驱动完整和非完整拉格朗日力学系统的简化[396],并为它们发展了非线性控制方法。他在约相空间中使用反馈线性化来发展控制律[397]。不过,他只考虑交换对称群,而不研究非零动量系统。Grizzle以olfatis-saber的工作为基础,表明具有一个循环非驱动状态的平面机器人总是可以局部控制[398]。Chhabra和Emami开发了一种非完整多体系统的两阶动力学约简方法,重点讨论了一类在对称群作用下不变的分布[357]。在此过程中,他们考虑了多自由度关节,并使用了chaplygin和辛约简定理。在另一项工作中,他们也提出了一种具有完整关节和恒动量的多体系统的简化方法[399]。非零动量守恒是由第一个关节的相对构型流形的对称群作用引起的,辛约简可以用来表示系统在简化流形中的行为。该研究导致了第一个统一的输出跟踪控制结构的欠驱动,具有对称约束的机器人基于反馈线性化在减少相空间[400]。该控制在空间机械臂和漫游车系统中实现。Muralidharan对球形机器人实施了基于几何的非线性控制[350],以实现强可及性和小范围局部可控性。他证明了具有几乎全局吸引域的位置和姿态控制器的渐近稳定性。Khadem等人对非完整针转向控制器进行了几何简化,设计了一种两步控制方案,用于在稳定流形上移动针,该流形对应于插入和收回针[401]。Martinez和Cortes证明,通过拉格朗日简化机器人系统,运动概念自然地出现在最优控制问题中[384,402]。
7.2.5 先进的几何控制
正如Nakamura和Mukherjee[223]所研究的,仅使用关节的驱动就可以同时控制基体航天器和手臂的运动。Tortopidis和Papadopoulos开发了一种具有非完整约束的欠交流自由漂浮航天器机械臂并行解析路径规划逻辑[171]。受控拉格朗日法(Controlled Lagrangian Method, CLM),又称能量成形法,通常通过对输入能量和外部力函数进行成形来稳定拉格朗日系统[392]。Tashakory结合了CLM来控制臂动机器人[403]。Wee等人[246]论证了一种自适应运动控制逻辑,该逻辑使用参数估计律来寻找系统的未知参数,利用其几何物理特性,强调动量积分的使用。最近,在空间机器人处理样本(行星探测车)、卫星\碎片(OOS)甚至整个岩石物体(小行星采矿)的各个领域中,温和抓取方法越来越受欢迎[404]。包笼抓是最近开发的用于OOS任务的概念,使用蛇形欠驱动软臂轻轻地包围并捕获目标物体[405,406]。基于共形几何代数(CGA)的控制器在欠驱动仿蛇机器人中得到了广泛的应用,这些仿蛇机器人对笼式抓取具有重要意义。Hrdina使用Clifford代数(CGA的特殊应用)来解决欠驱动n连杆蛇形机器人的局部能控性问题[407]。他开发了一个三连杆蛇型机器人的控制方案,并证明了CGA简化了模型修改[349]。他还利用微分几何工具解决了三连杆蛇型机器人的局部可控性问题。此外,Navart和Matousek[408]演示了CGA(特别是5-D CGA)控制模拟三连杆机器人的能力。Guo等人[409]开发了一种蛇形机器人正反向引导运动规划方法。他们将Hamilton Jacobi Bellman方程结合在一个最优控制器中,并对其运动进行动力学减少,从而能够控制一条欠驱动的蛇。另一个抓握的想法是使用一系列中空末端执行器来固定不能抓握的物体的两端[410]。
8. 对环境干扰的鲁棒性
GNC系统负责规划和控制手臂和基本运动必须能够补偿系统中的不确定性和外部干扰。前者的例子是测量和执行器模型的不确定性[411,412],以及系统总动量(假定为守恒)中的缓慢漂移[413]。后者包括太阳辐射压力(Solar Radiation Pressure, SRP)、空气动力阻力(aerodynamic drag)、高阶引力效应(high order gravitational)和其他轨道扰动。SRP是航天器控制和设计文献中研究最深入的轨道扰动之一[414]。忽略这些扰动的影响将导致受控航天器机械臂系统偏离其预期行为[93]。在控制器设计中,手臂在底座上的耦合效应有时也被视为扰动源[101]。在运动方程中,由位场引起的重力和磁场扰动出现在![]() 矩阵中,而SRP (
矩阵中,而SRP (![]() )和拖动效应(
)和拖动效应(![]() )作为输入力输入在方程的右侧。
)作为输入力输入在方程的右侧。
8.1 轨道扰动源
太阳辐射压力是一种在地球同步轨道和较高高度轨道上最有效的相对知名的力,它是由来自太阳的光子对航天器的机体和面板的影响造成的。它取决于物体暴露在太阳下的横截面,因此,它不是一个均匀的力。然而,它会导致航天器轨道位置和更重要的是姿态的改变[415]。SRP的影响可以通过下面的方程来体现[416]:
其中,S是SRP暴露表面的面积,E是太阳辐照度,![]() 辐射的入射角,
辐射的入射角,![]() 是光在真空中的传播速度,
是光在真空中的传播速度,![]() 是镜面反射入射辐射的比例,这个力体现在表面S的法向为
是镜面反射入射辐射的比例,这个力体现在表面S的法向为![]() 和切线方向
和切线方向![]() 。虽然SRP在短期内影响不大,但在长期运行中,它会引起控制器行为的明显扰动[94]。轨道扰动可能包括由于地球扁率或其质量的非均匀分布而产生的高阶非线性引力效应[417]。一种表示高阶引力扰动的方法是通过球谐[418,419],其给出的引力势为
。虽然SRP在短期内影响不大,但在长期运行中,它会引起控制器行为的明显扰动[94]。轨道扰动可能包括由于地球扁率或其质量的非均匀分布而产生的高阶非线性引力效应[417]。一种表示高阶引力扰动的方法是通过球谐[418,419],其给出的引力势为
其中,![]() 为地球引力常数,
为地球引力常数,![]() 是到地心的距离,
是到地心的距离,![]() 是地球的参考半径,
是地球的参考半径,![]() 是地心共纬度,
是地心共纬度,![]() 是经度,
是经度,![]() 是完全归一化的,无单位的球谐系数度和阶,
是完全归一化的,无单位的球谐系数度和阶,![]() 为n自由度m阶完全归一化关联Legendre函数。
为n自由度m阶完全归一化关联Legendre函数。
在轨道环境中,特别是在LEO中,对任何机器人系统最主要的扰动之一是重力梯度力矩(![]() ),它在附着于系统的CoM的体坐标系中以以下形式出现:
),它在附着于系统的CoM的体坐标系中以以下形式出现:
其中,![]() 是轨道系轴在物体坐标系中的矢量表示,
是轨道系轴在物体坐标系中的矢量表示,![]() 是为航天器-机械臂系统关于其CoM的锁定惯量矩阵。撞击目标时的接触力,特别是在非合作目标[420]和小行星重定向[111]的情况下,是另一个主要的扰动源,可以估计如[296],必须由控制器加以纠正。
是为航天器-机械臂系统关于其CoM的锁定惯量矩阵。撞击目标时的接触力,特别是在非合作目标[420]和小行星重定向[111]的情况下,是另一个主要的扰动源,可以估计如[296],必须由控制器加以纠正。
恶劣的外太空环境(特别是磁暴[421])的磁干扰也是将任何系统送入轨道的不需要的外力的另一种来源,无论是单个卫星还是空间操纵器系统[422]。磁势,类似于重力扰动,已经用球谐子来表示[422]。在近地轨道上,阻力扰动也可能是相当大的,其日益增长的影响可能导致航天器操纵器系统状态的剧烈变化。
当忽略干扰时,航天器机械臂系统的CoM在轨道坐标系中被认为是固定的或匀速运动的,这是一个不准确的轨道实际系统模型。这些影响往往被忽ADCS系统通常被认为是活跃的。然而,对于以自由漂浮模式运行的完全自主机器人系统,需要同时控制基体\机械手运动和在敏感目标附近的GNC系统,应考虑干扰效应。航天器机械臂系统的研究很少考虑扰动[177,423]和不确定性的影响,在其动态规划GNC设计中。与简单的线性时不变反馈系统相比,自适应控制方法通常包含干扰以显示其鲁棒性和有效性[261]。
8.2 抑制干扰的控制方法
轨道扰动,如SRP、重力梯度(gravity)、空气动力阻力(aerodynamic drag )、磁力(magnetics)等,是最小的,经常被忽略[93]。目前大量可用的控制方法都是通过直接反馈控制方案[424]或专门设计用于抑制干扰[59]的最优控制器来处理机器人操作过程中的干扰。Rybus, Seweryn和Sasiadek所采用的最优控制方法(extended GJM)具有考虑外力的能力[177]。非线性控制器具有主动抵制外部对空间机械臂轨迹跟踪性能不利影响的潜力[353]。CMAC算法,如第7.1节所示,可以促进对不确定动力学的航天器的鲁棒控制[282]。基于SMC的控制器,由于其结构变化以响应意外干扰和建模缺陷,有望为在轨自由漂浮物提供鲁棒控制性能[425]。鲁棒控制器如![]() 、
、![]() 和
和![]() -合成是最有效的非线性控制器的一些提示位置跟踪柔性航天器[426, 427]。在识别阶段,考虑到外层空间的恶劣照明条件,鲁棒性甚至很重要。Aghili和Parsa使用视觉系统稳健地估计轨道目标的状态[57,67]。虽然它们包括了轨道力学的一些方面,以便进行更准确的估计,但它们没有包括环境扰动对目标动力学的任何影响。
-合成是最有效的非线性控制器的一些提示位置跟踪柔性航天器[426, 427]。在识别阶段,考虑到外层空间的恶劣照明条件,鲁棒性甚至很重要。Aghili和Parsa使用视觉系统稳健地估计轨道目标的状态[57,67]。虽然它们包括了轨道力学的一些方面,以便进行更准确的估计,但它们没有包括环境扰动对目标动力学的任何影响。
9. 结论
轨道任务,包括在轨服务、卫星\站的组装、探测外星物体和减缓空间碎片,经常作为空间探索和开发方案的一部分进行。这些任务在遥远和敌对的外层空间环境中执行,可以提供通用和自主的技术解决方案的空间操纵器大大有利于这些任务。本文件由两个部分组成,其重点是讨论在轨道任务中部署的空间机械臂的制导、导航和控制系统的作用。
在第一部分中,确定了在轨机器人任务的共同阶段,并对每个阶段开发的各类GNC方法进行了广泛的回顾。提出了一种航天器机械臂系统的运动学和动力学公式,以统一已报道的GNC方法的符号。这提供了关于GNC解决方案的不同系列的比较讨论,这些解决方案在每个部分的开始部分被总结在多个表中。本文重点研究了用于姿态同步、机械臂展开和捕获阶段的GNC方法,特别是用于空间机械臂自由漂浮和自由飞行两种工作状态的GNC方法。自由漂浮系统需要补偿由于臂的运动引起的对基地航天器的干扰反应。本文详细讨论了许多评估和处理此类扰动的GNC技术,如GJM、RNS、扰动映射和最优控制。自由飞行系统使用一个单独的控制通道来保持基地航天器的静止,因此,它们的手臂GNC只能集中于末端执行器运动的控制。然而,基础控制可能导致相当大的燃料消耗,并可能将系统推向不稳定的区域。还研究了用于自由飞行系统的GNC技术,其中大多数与用于自由漂浮系统的GNC技术性质相似。外层空间环境和轨道目标的部分已知性质要求采用适应性强和稳健的GNC方法。各种自适应、鲁棒、变结构和其他不确定性\干扰拒绝GNC技术得到了广泛的回顾。手臂、关节或目标的柔性对GNC系统的性能有不可忽视的影响,这在文献中得到了广泛的研究。这种影响将在本文的某些部分单独讨论。要想抓住目标,需要事先进行大量细致的计划。据报道,GNC方法计划的前抓轨要么是最小化冲击力,要么是最大化末端执行器顺应性,以吸收冲击。类似地,后抓GNC技术已经被设计用来抑制未知的,不需要的翻滚运动的目标。
在本文的第二部分,作者对自主在轨机器人GNC系统的未来发展进行了详细的展望,并深入探讨了人工智能和几何力学的应用。列举了空间机器人可能应用或不应用的各种现有方法,并讨论了它们在空间机械臂GNC中的潜在应用。报道了每种方法在在轨机器人任务GNC中克服障碍的能力,说明了它们在简化、加强或数值增强GNC程序方面的优点。论文最后对轨道扰动及其对空间机器人系统长期自治的风险进行了单独讨论。
竞争利益声明:
作者声明,他们没有已知的相互竞争的经济利益或个人关系,可能已经影响了本文报告的工作。
参考文献:
[1] A. Flores-Abad, O. Ma, K. Pham, S. Ulrich, A review of space robotics technologies for on-orbit servicing, Prog. Aerosp. Sci. 68 (2014) 1 26.
[2] A. Meintel, Remote orbital servicing system concept, in: Satellite Services Workshop, NASA Johnson Space Center, Houston, TX, 1982, 1982.
[3] C.M. Hinds, Satellite servicing, 1982, Google Patents, US Patent 4, 349, 837.
[4] D.L. Akin, M. Minsky, E. Thiel, C. Kurtzman, Space applications of automation, robotics and machine intelligence systems (ARAMIS), phase 2. volume 1: Telepresence technology base development, Technical Report, Massachusetts Inst. of Tech.; Space Systems Lab., NASA, 1983.
[5] M. Bronez, M. Clarke, A. Quinn, Requirements development for a free-flying robot the robin", in: International Conference on Robotics and Automation, 7-10 April 1986, San Francisco, California, USA, 1986.
[6] W. Xu, B. Liang, B. Li, Y. Xu, A universal on-orbit servicing system used in the geostationary orbit, Adv. Space Res. 48 (1) (2011) 95 119.
[7] D.J. Kessler, B.G. Cour-Palais, Collision frequency of artificial satellites: The creation of a debris belt, J. Geophys. Res. Space Phys. 83 (A6) (1978) 2637 2646.
[8] K. Hovell, S. Ulrich, Attitude stabilization of an unknown and spinning target spacecraft using a visco-elastic tether, in: 13th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, Netherlands, 11 May 2015, 2015, pp. 1 8.
[9] E.J. van der Heide, M. Kruijff, Tethers and debris mitigation, Acta Astronaut. (ISSN: 0094-5765) 48 (5) (2001) 503 516.
[10] V. Aslanov, V. Yudintsev, Dynamics of large space debris removal using tethered space tug, Acta Astronaut. 91 (2013) 149 156.
[11] V.S. Aslanov, V.V. Yudintsev, Behavior of tethered debris with flexible appendages, Acta Astronaut. 104 (1) (2014) 91 98.
[12] V.S. Aslanov, V.V. Yudintsev, The motion of tethered tug debris system with fuel residuals, Adv. Space Res. 56 (7) (2015) 1493 1501.
[13] K. Hovell, S. Ulrich, Attitude stabilization of an uncooperative spacecraft in an orbital environment using visco-elastic tethers, in: AIAA Guidance, Navigation, and Control Conference, San Diego, California, USA, 4-8 January 2016, 2016, p. 0641.
[14] S. Kawamoto, Y. Ohkawa, S. Kitamura, S. ichiro Nishida, Strategy for active debris removal using electrodynamic tether, Trans. Japan Soc. Aeronaut. Space Sci. Space Technol. Japan 7 (ists26) (2009).
[15] C. Bombardelli, J. Peláez, Ion beam shepherd for asteroid deflection, J. Guid. Control Dyn. 34 (4) (2011) 1270 1272.
[16] J. Reed, S. Barraclough, Development of harpoon system for capturing space debris, in: 6th European Conference on Space Debris, Darmstadt, Germany, 22-25 April 2013, in: ESA Special Publication, vol. 723, 2013, p. 174.
[17] R. Dudziak, S. Tuttle, S. Barraclough, Harpoon technology development for the active removal of space debris, Adv. Space Res. 56 (3) (2015) 509 527.
[18] J. Reed, J. Busquets, C. White, Grappling system for capturing heavy space debris, in: 2nd European Workshop on Active Debris Removal, 18 June 2012, Centre National d Etudes Spatiales Paris, France, 2012, pp. 18 19.
[19] L. Visagie, V. Lappas, S. Erb, Drag sails for space debris mitigation, Acta Astronaut. (ISSN: 0094-5765) 109 (2015) 65 75.
[20] K. Yoshida, Engineering test satellite VII flight experiments for space robot dynamics and control: theories on laboratory test beds ten years ago, now in orbit, Int. J. Robot. Res. 22 (5) (2003) 321 335.
[21] I. Kawano, M. Mokuno, T. Kasai, T. Suzuki, Result of autonomous rendezvous docking experiment of engineering test satellite-VII, J. Spacecr. Rockets 38 (1) (2001) 105 111.
[22] J. Kawaguchi, A. Fujiwara, T. Uesugi, Hayabusa Its technology and science accomplishment summary and hayabusa-2, Acta Astronaut. 62 (10 11) (2008) 639 647.
[23] Y. Tsuda, T. Saiki, F. Terui, S. Nakazawa, M. Yoshikawa, S.-i. Watanabe, H.P. Team, Hayabusa2 mission status: Landing, roving and cratering on asteroid ryugu, Acta Astronaut. 171 (2020) 42 54.
[24] T. Yamaguchi, T. Saiki, S. Tanaka, Y. Takei, T. Okada, T. Takahashi, Y. Tsuda, Hayabusa2-ryugu proximity operation planning and landing site selection, Acta Astronaut. 151 (2018) 217 227.
[25] F. Terui, N. Ogawa, G. Ono, S. Yasuda, T. Masuda, K. Matsushima, T. Saiki, Y. Tsuda, Guidance, navigation, and control of hayabusa2 touchdown operations, Astrodynamics 4 (4) (2020) 393 409.
[26] A. May, B. Sutter, T. Linn, B. Bierhaus, K. Berry, R. Mink, OSIRIS-REx touch- and-go (TAG) mission design for asteroid sample collection, 65th International Astronautical Congress; September 29, 2014 - October 03, 2014; Toronto; Canada, 2014.
[27] J.R. Brophy, B. Muirhead, Near-earth asteroid retrieval mission (arm) study, in: 33rd International Electric Propulsion Conference, Washington, DC, October 6 10, 2013, 2013.
[28] E.T. Lu, S.G. Love, Gravitational tractor for towing asteroids, Nature 438 (7065) (2005) 177.
[29] M. Vasile, C.A. Maddock, On the deflection of asteroids with mirrors, Celestial Mech. Dynam. Astronom. 107 (1 2) (2010) 265 284.
[30] A. Gibbings, M. Vasile, I. Watson, J.-M. Hopkins, D. Burns, Experimental analysis of laser ablated plumes for asteroid deflection and exploitation, Acta Astronaut. 90 (1) (2013) 85 97.
[31] M. Vasile, C. Colombo, Optimal impact strategies for asteroid deflection, J. Guid. Control Dyn. 31 (4) (2008) 858 872.
[32] D. King, Space servicing: past, present and future, in: The 6th International Symposium on Artificial Intelligence and Robotics & Automation in Space: I- SAIRAS, Canadian Space Agency, St-Hubert, Quebec, Canada, 18-22 June 2001, 2001, pp. 18 22.
[33] B.A. Aikenhead, R.G. Daniell, F.M. Davis, Canadarm and the space shuttle, J. Vacuum Sci. Technol. Vacuum Surf. Films 1 (2) (1983) 126 132.
[34] G. Gibbs, S. Sachdev, Canada and the international space station program: overview and status, Acta Astronaut. 51 (1 9) (2002) 591 600.
[35] E. Coleshill, L. Oshinowo, R. Rembala, B. Bina, D. Rey, S. Sindelar, Dextre: Improving maintenance operations on the international space station, Acta Astronaut. 64 (9 10) (2009) 869 874.
[36] V. Abbasi, B. Azria, E. Tabarah, V. Menon, E. Phillips, M. Bedirian, Improved 7-DOF control of ISS robotic manipulators, in: Space OPS 2004 Conference, 17 - 21 May 2004 Montreal, Quebec, Canada, 2004, p. 407.
[37] F. Kendoul, Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems, J. Field Robotics 29 (2) (2012) 315 378.
[38] I. Rekleitis, E. Martin, G. Rouleau, R. L Archevêque, K. Parsa, E. Dupuis, Autonomous capture of a tumbling satellite, J. Field Robotics 24 (4) (2007) 275 296.
[39] J. Padial, M. Hammond, S. Augenstein, S.M. Rock, Tumbling target reconstruc- tion and pose estimation through fusion of monocular vision and sparse-pattern range data, in: International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Hamburg, Germany, 13-15 Sept. 2012, IEEE, 2012, pp. 419 425.
[40] W. Lu, Y. Geng, X. Chen, F. Zhang, Relative position and attitude coupled control for autonomous docking with a tumbling target, Int. J. Control Autom. 4 (4) (2011) 1 22.
[41] H. Park, R. Zappulla, C. Zagaris, J. Virgili-Llop, M. Romano, Nonlinear model predictive control for spacecraft rendezvous and docking with a rotating target, Adv. Astron. Sci. 160 (May) (2017) 1135 1148.
[42] S. Nolet, E. Kong, D.W. Miller, Design of an algorithm for autonomous docking with a freely tumbling target, in: SPIE 5799 Modeling, Simulation, and Verification of Space-Based Systems II, Orlando, Florida, United States, 19 May 2005, 5799, International Society for Optics and Photonics, 2005, pp. 123 134.
[43] S. Nolet, Development of a guidance, navigation and control architecture and validation process enabling autonomous docking to a tumbling satellite (Ph.D. thesis), Massachusetts Institute of Technology, 2007.
[44] J. Michael, K. Chudej, M. Gerdts, J. Pannek, Optimal rendezvous path planning to an uncontrolled tumbling target, IFAC Proc. Vol. 46 (19) (2013) 347 352.
[45] G. Boyarko, O. Yakimenko, M. Romano, Optimal rendezvous trajectories of a controlled spacecraft and a tumbling object, J. Guid. Control Dyn. (ISSN: 0731-5090) 34 (4) (2011) 1239 1252,
[46] D.C. Woffinden, D.K. Geller, Navigating the road to autonomous orbital rendezvous, J. Spacecr. Rockets 44 (4) (2007) 898 909.
[47] G. Xing, S. Parvez, Relative attitude kinematics & dynamics equations and its applications to spacecraft attitude state capture and tracking in large angle slewing maneuvers, in: Space Control Conference, 13 April 1999, 1999, p. 105.
[48] J. Michael, K. Chudej, J. Pannek, Modelling and optimal control of a docking maneuver with an uncontrolled satellite, IFAC Proc. Vol, 45 (2) (2012) 1135 1140.
[49] J. Michael, K. Chudej, M. Gerdts, J. Pannek, Optimal rendezvous path planning to an uncontrolled tumbling target, IFAC Proc. Vol. 46 (19) (2013) 347 352.
[50] H. Benninghoff, T. Boge, F. Rems, Autonomous navigation for on-orbit servicing, KI - Künst. Intell. (ISSN: 1610-1987) 28 (2) (2014) 77 83.
[51] J. Virgili-Llop, C. Zagaris, R.I. Zappulla, A. Bradstreet, M. Romano, Convex optimization for proximity maneuvering of a spacecraft with a robotic manipu- lator, in: Proceedings of the 27th AAS/AIAA Spaceflight Mechanics Meeting, San Antonio, TX, Feb. 6-9, 2017. (Advances in the Astronautical Sciences, Volume 160, 2017, pp. 1059-1078).
[52] F. Rems, J. Moreno Gonzalez, T. Boge, S. Tuttas, U. Stilla, Fast initial pose estimation of spacecraft from lidar point cloud data, in: 13th Symposium on Advanced Space Technologies in Robotics and Automation, 11-13 May 2015, Nordwijk, Netherlands., 2015.
[53] F. Rems, E. Risse, H. Benninghoff, Rendezvous GNC-system for autonomous orbital servicing of uncooperative targets, in: Proceedings of the 10th Interna- tional ESA Conference on Guidance, Navigation and Control Systems, Salzburg, Austria, 29 May - 2 June 2017, 2017.
[54] H. Benninghoff, T. Boge, F. Rems, Autonomous navigation for on-orbit servicing, KI-Künst. Intell. 28 (2) (2014) 77 83.
[55] D. Fourie, B. Tweddle, S. Ulrich, A. Saenz Otero, Vision-based relative naviga- tion and control for autonomous spacecraft inspection of an unknown object, in: AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, 15 Aug 2013, 2013, p. 4759.
[56] M. Fiala, Artag fiducial marker system applied to vision based spacecraft docking, in: Intl. Conf. Intelligent Robots and Systems (IROS) 2005 Workshop on Robot Vision for Space Applications, 2 August 2005, Edmonton, Alberta, Canada, 2005, pp. 35 40.
[57] F. Aghili, K. Parsa, An adaptive Kalman filter for motion esitmation/prediction of a free-falling space object using laser-vision data with uncertain inertial and noise characteristics, in: AIAA Guidance, Navigation and Control Conference and Exhibit, 18 - 21 August 2008, Honolulu, Hawaii, 2008, p. 7317.
[58] F. Aghili, Automated rendezvous & docking (aR&D) without impact using a reliable 3D vision system, in: AIAA Guidance, Navigation, and Control Conference, 2 - 5 August 2010, Toronto, Ontario, Canada, 2010, p. 7602.
[59] F. Aghili, C.-Y. Su, Robust relative navigation by integration of ICP and adaptive Kalman filter using laser scanner and IMU, IEEE/ASME Trans. Mech. 21 (4) (2016) 2015 2026.
[60] F.Z. Qureshi, D. Terzopoulos, P. Jasiobedzki, A cognitive vision system for space robotics, in: Proceedings of the ECCV 2004 Workshop on Applications of Computer Vision, Prague, 16 May 2004, 2004, pp. 120 128.
[61] D.N. Nenchev, K. Yoshida, Impact analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse, IEEE Trans. Robot. Autom. 15 (3) (1999) 548 557.
[62] P. Jasiobedski, M. Greenspan, G. Roth, Pose determination and tracking for autonomous satellite capture, National Research Council of Canada, 2001.
[63] F. Aghili, M. Kuryllo, G. Okouneva, C. English, Fault-tolerant position/attitude estimation of free-floating space objects using a laser range sensor, IEEE Sens. J. 11 (1) (2011) 176 185.
[64] F. Aghili, M. Kuryllo, G. Okouneva, C. English, Robust vision-based pose estima- tion of moving objects for automated rendezvous & docking, in: International Conference on Mechatronics and Automation, Xi an, China, 4-7 Aug. 2010, IEEE, 2010, pp. 305 311.
[65] S. Ruel, C. English, M. Anctil, J. Daly, C. Smith, S. Zhu, Real-time 3D vision solution for on-orbit autonomous rendezvous and docking, in: Proceedings of SPIE 6220, Spaceborne Sensors III, Orlando (Kissimmee), Florida, United States, 19 May 2006, Vol. 6220, 2006, 622009.
[66] F. Aghili, M. Kuryllo, G. Okouneva, C. English, Fault-tolerant pose estima- tion of space objects, in: International Conference on Advanced Intelligent Mechatronics, Montreal, on, Canada, 6-9 July 2010, IEEE, 2010, pp. 947 954.
[67] F. Aghili, K. Parsa, Motion and parameter estimation of space objects using laser-vision data, J. Guid. Control Dyn. 32 (2) (2009) 538 550.
[68] F. Aghili, K. Parsa, E. Martin, Robotic docking of a free-falling space object with occluded visual condition, in: Proc. Int. Symp. Artificial Intell. Robot. Automat. in Space (I-SAIRAS), Hollywood, USA February 26 - 29, 2008, 2008.
[69] A. Shademan, A.-m. Farahmand, M. Jägersand, Robust Uncalibrated Visual Servoing for Autonomous On-Orbit-Servicing, in: Proceedings of the I-SAIRAS, Sapporo, Japan August 29 - September 1, 2010.
[70] W. Xu, B. Liang, C. Li, W. Qiang, Y. Xu, K.K. Lee, Non-holonomic path planning of space robot based on genetic algorithm, in: International Conference on Robotics and Biomimetics, Kunming, China, 17-20 Dec. 2006, IEEE, 2006, pp. 1471 1476.
[71] S. Yazdkhasti, S. Ulrich, J.Z. Sasiadek, Laboratory experimentation of stereo vision-based relative navigation with unknown spinning spacecraft, in: 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 24-27 Aug. 2015, IEEE, 2015, pp. 180 185.
[72] D. Fourie, B.E. Tweddle, S. Ulrich, A. Saenz-Otero, Flight results of vision-based navigation for autonomous spacecraft inspection of unknown objects, J. Spacecr. Rockets 51 (6) (2014) 2016 2026.
[73] G.J. Arantes, Rendezvous with a non-cooperating target (Ph.D. thesis), Universität Bremen, 2011.
[74] N.W. Oumer, Visual tracking and motion estimation for an on-orbit servicing of a satellite, (Ph.D. thesis), Universität Osnabrück, 2016.
[75] J.-F. Shi, S. Ulrich, S. Ruel, Spacecraft pose estimation using principal com- ponent analysis and a monocular camera, in: AIAA Guidance, Navigation, and Control Conference, Grapevine, Texas, 9 - 13 January 2017, 2017, p. 1034.
[76] S. Jaekel, R. Lampariello, W. Rackl, M. De Stefano, A.M. Giordano, O. Porges, M. Pietras, N. Oumer, B. Brunner, J. Ratti, et al., Design and operational elements of the robotic subsystem for the e. deorbit debris removal mission, Front. Robot. AI 5 (2018) 100.
[77] F. Aghili, A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics, IEEE Trans. Robotics 28 (3) (2012) 634 649.
[78] M. Al-isawi, J. Sasiadek, Guidance and control of a robot capturing an uncooperative space target, J. Intell. Robot. Syst. (2018). [79] F. Aghili, K. Parsa, An adaptive vision system for guidance of a robotic manipulator to capture a tumbling satellite with unknown dynamics, in: International Conference on Intelligent Robots and Systems, Nice, France, 22-26 Sept. 2008, IEEE, 2008, pp. 3064 3071.
[80] G. Dong, Z.H. Zhu, Autonomous robotic capture of non-cooperative target by adaptive extended Kalman filter based visual servo, Acta Astronaut. 122 (2016) 209 218.
[81] M. Zarei-Jalalabadi, S.M.-B. Malaek, Motion estimation of uncooperative space objects: A case of multi-platform fusion, Adv. Space Res. 62 (9) (2018) 2665 2678.
[82] M. Zarei-Jalalabadi, S.M.-B. Malaek, Modification of unscented Kalman filter using a set of scaling parameters, IET Signal Process. 12 (4) (2017) 471 480.
[83] M. Zarei-Jalalabadi, S.M. Malaek, S.S. Kia, A track-to-track fusion method for tracks with unknown correlations, IEEE Control Syst. Lett. 2 (2) (2017) 189 194.
[84] M. Zarei-Jalalabadi, S.M.-B. Malaek, Practical method to predict an upper bound for minimum variance track-to-track fusion, IET Signal Process. 11 (8) (2017) 961 968.
[85] F. Cavenago, Towards safe and reliable on-orbit autonomous operations with manipulators (Ph.D. thesis), Politecnico di Milano, 2020.
[86] T.V. Peters, Formation flying guidance for space debris observation, manipula- tion and capture, in: Astrodynamics Network AstroNet-II, Springer, 2016, pp. 225 239.
[87] P. Colmenarejo, G. Binet, L. Strippoli, T. Peters, M. Graziano, GNC aspects for active debris removal, in: Proceedings of the EuroGNC 2013, 2nd CEAS Specialist Conference on Guidance, Navigation & Control, Delft, Netherlands, 10-12 April 2013, 2013.
[88] K. Subbarao, S.J. Welsh, Nonlinear control of motion synchronization for satellite proximity operations, J. Guid. Control Dyn. 31 (5) (2008) 1284 1294.
[89] S. Welsh, K. Subbarao, Adaptive synchronization and control of free flying robots for capture of dynamic free-floating spacecrafts, in: AIAA/AAS Astro- dynamics Specialist Conference and Exhibit, Providence, Rhode Island, 16 - 19 August 2004, 2004, p. 5298.
[90] K. Yoshida, H. Nakanishi, H. Ueno, N. Inaba, T. Nishimaki, M. Oda, Dynamics and control for robotic capture of a non-cooperative satellite, in: Proc. I-SAIRAS, Nara, Japan, May 19 - 23, 2003, Vol. 3, pp. 1 8.
[91] S. Dubowsky, E. Papadopoulos, The kinematics, dynamics, and control of free- flying and free-floating space robotic systems, IEEE Trans. Robot. Autom. 9 (5) (1993) 531 543.
[92] T. Rybus, K. Seweryn, J.Z. Sźsiadek, Application of trajectory optimization method for a space manipulator with four degrees of freedom, in: 13th Interna- tional Conference on Informatics in Control, Automation and Robotics, Lisboa, Portugal, 29 -31 July 2016, SciTePress-Science and Technology Publications, Lda, 2016, pp. 92 101.
[93] A. Ellery, Tutorial review on space manipulators for space debris mitigation, Robotics 8 (2) (2019) 34.
[94] N. Ives, The effect of solar radiation pressure on the attitude control of an artificial earth satellite, London: Her Majesty s Stationary Office, 1963.
[95] E.G. Kaigom, T.J. Jung, J. Roßmann, Optimal motion planning of a space robot with base disturbance minimization, in: 11th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, the Netherlands, 12 - 15 April 2011, 2011, pp. 1 6.
[96] N. Inaba, M. Oda, Autonomous satellite capture by a space robot: world first on-orbit experiment on a Japanese robot satellite ETS-vii, in: ICRA. Millennium Conference. International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24 April 2000, 2, 2000, pp. 1169 1174 vol.2.
[97] P. Huang, Y. Xu, B. Liang, Tracking trajectory planning of space manipulator for capturing operation, Int. J. Adv. Robot. Syst. 3 (3) (2006) 31.
[98] T. Rybus, K. Seweryn, Manipulator trajectories during orbital servicing mission: numerical simulations and experiments on microgravity simulator, in: Progress in Flight Dynamics, Guidance, Navigation, and Control Volume 10, 10, EDP Sciences, 2018, pp. 239 264.
[99] Z. Vafa, S. Dubowsky, On the dynamics of manipulators in space using the virtual manipulator approach, in: International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March-3 April 1987, 4, IEEE, 1987, pp. 579 585.
[100] M.A. Torres, S. Dubowsky, Minimizing spacecraft attitude disturbances in space manipulator systems, J. Guid. Control Dyn. 15 (4) (1992) 1010 1017.
[101] S. Dubowsky, M.A. Torres, Path planning for space manipulators to mini- mize spacecraft attitude disturbances, in: International Conference on Robotics and Automation, Sacramento, CA, USA, 9-11 April 1991, IEEE, 1991, pp. 2522 2528.
[102] R. Chhabra, A unified geometric framework for kinematics, dynamics and concurrent control of free-base, open-chain multi-body systems with holonomic and nonholonomic constraints (Ph.D. thesis), University of Toronto, 2014.
[103] H. Nagamatsu, T. Kubota, I. Nakatani, Capture strategy for retrieval of a tumbling satellite by a space robotic manipulator, in: International Conference on Robotics and Automation, Minneapolis, MN, USA, 22-28 April 1996, 1, IEEE, 1996, pp. 70 75.
[104] S. Liu, L. Wu, Z. Lu, Impact dynamics and control of a flexible dual-arm space robot capturing an object, Appl. Math. Comput. 185 (2) (2007) 1149 1159.
[105] W. Cheng, L. Tianxi, Z. Yang, Grasping strategy in space robot capturing floating target, Chin. J. Aeronaut. 23 (5) (2010) 591 598.
[106] K. Yoshida, H. Nakanishi, Impedance matching in capturing a satellite by a space robot, in: International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453), Las Vegas, NV, USA, 27-31 Oct. 2003, 4, IEEE, 2003, pp. 3059 3064.
[107] P.J. Staritz, S. Skaff, C. Urmson, W. Whittaker, Skyworker: a robot for assembly, inspection and maintenance of large scale orbital facilities, in: ICRA. Interna- tional Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, South Korea, South Korea, 21-26 May 2001, 4, IEEE, 2001, pp. 4180 4185.
[108] P. Tsiotras, A. De Nailly, Comparison between peer-to-peer and single-spacecraft refueling strategies for spacecraft in circular orbits, in: Infotech@ Aerospace, Arlington, Virginia, 26 - 29 September 2005, 2005, p. 7115.
[109] D. Zimpfer, P. Kachmar, S. Tuohy, Autonomous rendezvous, capture and in- space assembly: past, present and future, in: 1st Space Exploration Conference: Continuing the Voyage of Discovery, Orlando, Florida, 30 January 2005 - 01 February 2005, 2005, p. 2523.
[110] K. Yoshida, H. Nakanishi, H. Ueno, N. Inaba, T. Nishimaki, M. Oda, Dynamics, control and impedance matching for robotic capture of a non-cooperative satellite, Adv. Robot. 18 (2) (2004) 175 198.
[111] M. Shan, J. Guo, E. Gill, Review and comparison of active space debris capturing and removal methods, Prog. Aerosp. Sci. 80 (2016) 18 32.
[112] M. Wang, J. Luo, J. Yuan, U. Walter, Detumbling strategy and coordination control of kinematically redundant space robot after capturing a tumbling target, Nonlinear Dynam. (ISSN: 1573-269X) 92 (3) (2018) 1023 1043.
[113] D.N. Dimitrov, K. Yoshida, Momentum distribution in a space manipulator for facilitating the post-impact control, in: International Conference One Intelligent Robots and Systems (IROS)(IEEE Cat. No. 04CH37566), Sendai, Japan, 28 Sept.-2 Oct. 2004, 4, IEEE, 2004, pp. 3345 3350.
[114] I. Sharf, P. Woo, T.-C. Nguyen-Huynh, A. Misra, System rigidization and control for post-capture maneuvering of large space debris, in: Aerospace Conference, Big Sky, MT, USA, 5-12 March 2016, IEEE, 2016, pp. 1 12.
[115] X. Cyril, A.K. Misra, M. Ingham, G.J. Jaar, Postcapture dynamics of a spacecraft-manipulator-payload system, J. Guid. Control Dyn. 23 (1) (2000) 95 100.
[116] X. Cyril, G.J. Jaar, A.K. Misra, The effect of payload impact on the dynamics of a space robot, in: International Conference on Intelligent Robots and Systems (IROS 93), Yokohama, Japan, 26-30 July 1993, 3, IEEE, 1993, pp. 2070 2075.
[117] Y. Murotsu, K. Senda, M. Ozaki, S. Tsujio, Parameter identification of unknown object handled by free-flying space robot, J. Guid. Control Dyn. 17 (3) (1994) 488 494.
[118] F. Aghili, Coordination control of a free-flying manipulator and its base attitude to capture and detumble a noncooperative satellite, in: International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10-15 Oct. 2009, IEEE, 2009, pp. 2365 2372.
[119] F. Aghili, Optimal control of a space manipulator for detumbling of a target satellite, in: International Conference on Robotics and Automation, Kobe, Japan, 12-17 May 2009, IEEE, 2009, pp. 3019 3024.
[120] P. Gasbarri, A. Pisculli, Dynamic/control interactions between flexible orbit- ing space-robot during grasping, docking and post-docking manoeuvres, Acta Astronaut. 110 (2015) 225 238.
[121] S. Abiko, G. Hirzinger, On-line parameter adaptation for a momentum control in the post-grasping of a tumbling target with model uncertainty, in: International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 Oct.-2 Nov. 2007, IEEE, 2007, pp. 847 852.
[122] W. Rackl, R. Lampariello, A. Albu-Schäffer, Parameter identification methods for free-floating space robots with direct torque sensing, in: 19th IFAC Symposium on Automatic Control in Aerospace, Würzburg, Germany, 2-6 September 2013, Vol. 46, (19) Elsevier, 2013, pp. 464 469.
[123] T.C. Nguyen-Huynh, I. Sharf, Adaptive reactionless motion and parameter identification in postcapture of space debris, J. Guid. Control Dyn. 36 (2) (2013) 404 414.
[124] A. Ellery, An engineering approach to the dynamic control of space robotic on-orbit servicers, Proc. Inst. Mech. Eng. Part G 218 (2) (2004) 79 98.
[125] R.M. Murray, Z. Li, S.S. Sastry, S.S. Sastry, A mathematical introduction to robotic manipulation, CRC press, 22 March 1994, 2017.
[126] S. Stramigioli, B. Maschke, C. Bidard, A hamiltonian formulation of the dynamics of spatial mechanisms using lie groups and screw theory, in: Proc. Symposium Commemorating the Legacy, Work and Life of Sir RS Ball, J. Duffy and H. Lipkin Organizers, 9-11 July 2000, University of Cambridge, Cambridge, U.K., 2000.
[127] R. Chhabra, M.R. Emami, A generalized exponential formula for forward and differential kinematics of open-chain multi-body systems, Mech. Mach. Theory 73 (2014) 61 75.
[128] Y.-w. Zhu, L.-p. Yang, 6-DOF synchronization control approach strategy for space robots capture mission, J. Nat. Univ. Defense Technol. 6 (2009).
[129] R. Liu, X. Cao, M. Liu, Finite-time synchronization control of spacecraft formation with network-induced communication delay, IEEE Access 5 (2017) 27242 27253.
[130] E.R. Burnett, H. Schaub, Spacecraft formation and orbit control using attitude- dependent solar radiation pressure, in: International Workshop on Satellite Constellations and Formation Flying, IAF Astrodynamics Committee, Glasgow, Scotland, 16 19 July 2019, 2019.
[131] P. C. Wang, F. Hadaegh, K. Lau, Synchronized formation rotation and attitude control of multiple free-flying spacecraft, J. Guid. Control Dyn. 22 (1) (1999) 28 35.
[132] J. Li, K.D. Kumar, Fault tolerant attitude synchronization control during formation flying, J. Aerosp. Eng. 24 (3) (2010) 251 263.
[133] B. Wu, D. Wang, E.K. Poh, Decentralized sliding-mode control for attitude synchronization in spacecraft formation, Internat. J. Robust Nonlinear Control 23 (11) (2013) 1183 1197.
[134] X.Y. An, W. Lu, Z. Ren, Compound control of attitude synchronization for autonomous docking to a tumbling satellite, in: Appl. Mech. Mater., 394, Trans Tech Publ, 2013, pp. 470 476.
[135] S.-J. Chung, U. Ahsun, J.-J.E. Slotine, Application of synchronization to for- mation flying spacecraft: Lagrangian approach, J. Guid. Control Dyn. 32 (2) (2009) 512 526
[136] K. Subbarao, J. McDonald, Multi-sensor fusion based relative navigation for synchronization and capture of free floating spacecraft, in: AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, 15 - 18 August 2005, 2005, p. 5858.
[137] Y.-H. Geng, W. Lu, X.-Q. Chen, Attitude synchronization control of on-orbit servicing spacecraft with respect to out-of-control target, Harbin Gongye Daxue Xuebao(J. Harbin Inst. Technol.) 44 (1) (2012) 1 6.
[138] A. Xueyan, R. Zhang, L. Wei, Terminal sliding mode control of attitude syn- chronization for autonomous docking to a tumbling satellite, in: International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20-22 Dec. 2013, IEEE, 2013, pp. 2760 2763.
[139] W. Lu, Y.H. Geng, X.W. Shan, Robust optimal sliding mode control for attitude synchronization of autonomous docking to a tumbling target, in: Appl. Mech. Mater., 157, Trans Tech Publ, 2012, pp. 757 761.
[140] P. Huang, Y. Xu, B. Liang, Tracking trajectory planning of space manipulator for capturing operation, Int. J. Adv. Robot. Syst. 3 (3) (2006) 31.
[141] G. Chamitoff, A. Saenz Otero, J. Katz, S. Ulrich, Admissible subspace trajectory optimizer (ASTRO) for autonomous robot operations on the space station, in: AIAA Guidance, Navigation, and Control Conference, National Harbor, Maryland, 13-17 January 2014, 2014, p. 1290.
[142] J.E. King, M. Klingensmith, C.M. Dellin, M.R. Dogar, P. Velagapudi, N.S. Pollard, S.S. Srinivasa, Pregrasp manipulation as trajectory optimization., in: Robotics: Science and Systems, Berlin, Germany, June 24 - June 28, 2013, 2013.
[143] A. Seddaoui, C. Saaj, H infinity control for a controlled floating robotic spacecraft, in: International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS), Madrid, Spain, 3 June 2018, 2018.
[144] S. Parsa, C.M. Saaj, H.R. Daniali, R. Ghaderi, On-orbit servicing: Novel algo- rithms for motion control of robot manipulators, in: Proc. 10th ESA Workshop on Advanced Space Technologies for Robotics and Automation, 11-13 November 2008, Noordwijk, the Netherlands, 2008.
[145] A. Seddaoui, C. Saaj, Optimised collision-free trajectory and controller design for robotic manipulators, in: 14th Symposium on Advanced Space Technologies in Robotics and Automation, 20th - 22nd June 2017, Leiden, Netherlands, 2017.
[146] F. Aghili, K. Parsa, Adaptive motion estimation of a tumbling satellite using laser-vision data with unknown noise characteristics, in: International Confer- ence on Intelligent Robots and Systems, San Diego, CA, USA, 29 Oct.-2 Nov. 2007, IEEE, 2007, pp. 839 846.
[147] D. Dimitrov, Dynamics and Control of Space Manipulators During a Satellite Capturing Operation (Ph.D. thesis), Department of Aerospace Engineering, Tohoku University, 2006.
[148] R. Lampariello, G. Hirzinger, Generating feasible trajectories for autonomous on-orbit grasping of spinning debris in a useful time, in: International Confer- ence on Intelligent Robots and Systems, Tokyo, Japan, 3-7 Nov. 2013, IEEE, 2013, pp. 5652 5659.
[149] V. Muralidharan, M.R. Emami, Rendezvous and attitude synchronization of a space manipulator, J. Astron. Sci. (2019) 1 21.
[150] E. Papadopoulos, S. Dubowsky, Dynamic singularities in free-floating space manipulators, in: Space Robotics: Dynamics and Control, Springer, 1993, pp. 77 100.
[151] K. Tchoń, W. Respondek, J. Ratajczak, Normal forms and configuration sin- gularities of a space manipulator, J. Intell. Robot. Syst. 93 (3 4) (2019) 621 634. [152] E. Papadopoulos, I. Papadimitriou, I. Poulakakis, Polynomial-based obstacle avoidance techniques for nonholonomic mobile manipulator systems, Robot. Auton. Syst. 51 (4) (2005) 229 247.
[153] T. Rybus, Obstacle avoidance in space robotics: Review of major challenges and proposed solutions, Prog. Aerosp. Sci. 101 (2018) 31 48.
[154] Y. Umetani, K. Yoshida, et al., Resolved motion rate control of space manipula- tors with generalized Jacobian matrix, IEEE Trans. Robot. Autom. 5 (3) (1989) 303 314.
[155] F. Aghili, K. Parsa, A reconfigurable robot with lockable cylindrical joints, IEEE Trans. Robot. 25 (4) (2009) 785 797.
[156] F. Aghili, C. Su, Reconfigurable space manipulators for in-orbit servicing and space exploration, in: International Conference on Intelligent Robotics and Applications, 3-5 October 2012, Montreal, QC, Canada, 2012.
[157] B. Bandyopadhyay, V. Thakar, C. Saaj, S. Janardhanan, Algorithm for comput- ing sliding mode control and switching surface from output samples, in: Proc. 8th IEEE Variable Structure Systems Workshop, Vilanova I la Geltru, Spain, Sep 6 - 8, 2004, Vol. 31.
[158] S. Ulrich, J.Z. Sasiadek, On the simple adaptive control of flexible-joint space manipulators with uncertainties, in: Aerospace Robotics II, Springer, 2015, pp. 13 23.
[159] S. Ulrich, J.Z. Sasiadek, I. Barkana, Nonlinear adaptive output feedback control of flexible-joint space manipulators with joint stiffness uncertainties, J. Guid. Control Dyn. 37 (6) (2014) 1961 1975.
[160] J.Z. Sasiadek, R. Srinivasan, Dynamic modeling and adaptive control of a single-link flexible manipulator, J. Guid. Control Dyn. 12 (6) (1989) 838 844.
[161] E. Papadopoulos, S.A.A. Moosavian, Dynamics and control of space free-flyers with multiple manipulators, Adv. Robot. 9 (6) (1994) 603 624.
[162] B. Pond, I. Sharf, Motion planning for flexible manipulators, in: International Conference on Systems, Man and Cybernetics. Intelligent Systems for the 21st Century, Vancouver, BC, Canada, 22-25 Oct. 1995, 3, IEEE, 1995, pp. 2103 2108.
[163] Y. Ishijima, D. Tzeranis, S. Dubowsky, The on-orbit maneuvering of large space flexible structures by free-flying robots, in: The 8th International Symposium on Artificial Intelligence, Robotics and Automation in Space, Munich, Germany, 5-8 September 2005, 2005.
[164] Y.-s. Guo, L. Chen, Terminal sliding mode control for coordinated motion of a space rigid manipulator with external disturbance, Appl. Math. Mech. 29 (5) (2008) 583.
[165] B.S. Chen, T.-S. Lee, J.-H. Feng, A nonlinear h infinity control design in robotic systems under parameter perturbation and external disturbance, Internat. J. Control 59 (2) (1994) 439 461.
[166] M.C. Saaj, B. Bandyopadhyay, H. Unbehauen, A new algorithm for discrete- time sliding-mode control using fast output sampling feedback, IEEE Trans. Ind. Electron. 49 (3) (2002) 518 523.
[167] S. Ulrich, J.Z. Sasiadek, Modified simple adaptive control for a two-link space robot, in: Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June-2 July 2010, IEEE, 2010, pp. 3654 3659.
[168] S. Ulrich, D.L. Hayhurst, A. Saenz Otero, D. Miller, I. Barkana, Simple adaptive control for spacecraft proximity operations, in: AIAA Guidance, Navigation, and Control Conference, National Harbor, Maryland, 13-17 January 2014, 2014, p. 1288.
[169] S. Mobayen, F. Tchier, Nonsingular fast terminal sliding-mode stabilizer for a class of uncertain nonlinear systems based on disturbance observer, Sci. Iran. Trans. D 24 (3) (2017) 1410 1418.
[170] X. Xi, S. Mobayen, H. Ren, S. Jafari, Robust finite-time synchronization of a class of chaotic systems via adaptive global sliding mode control, J. Vib. Control 24 (17) (2018) 3842 3854.
[171] I. Tortopidis, E. Papadopoulos, Point-to-point planning: methodologies for underactuated space robots, in: International Conference on Robotics and Automation, Orlando, FL, USA, 15-19 May 2006, IEEE, 2006, pp. 3861 3866.
[172] E.G. Papadopoulos, On the dynamics and control of space manipulators (Ph.D. thesis), Massachusetts Institute of Technology, 1990.
[173] E. Papadopoulos, S. Dubowsky, et al., On the nature of control algorithms for free-floating space manipulators., IEEE Trans. Robot. Autom. 7 (6) (1991) 750 758.
[174] X. Huang, Y. Jia, S. Xu, Path planning of a free-floating space robot based on the degree of controllability, Sci. China Technol. Sci. 60 (2) (2017) 251 263.
[175] X. Zhang, J. Liu, Effective motion planning strategy for space robot capturing targets under consideration of the berth position, Acta Astronaut. 148 (2018) 403 416.
[176] K. Yoshida, Space robot dynamics and control: To orbit, from orbit, and future, in: Robotics Research, Springer, 2000, pp. 449 456.
[177] T. Rybus, K. Seweryn, J.Z. Sasiadek, Trajectory optimization of space manipu- lator with non-zero angular momentum during orbital capture maneuver, in: AIAA Guidance, Navigation, and Control Conference, San Diego, California, USA, 4-8 January 2016, 2016, p. 0885.
[178] P. Huang, M. Wang, Z. Meng, F. Zhang, Z. Liu, H. Chang, Reconfigurable space- craft attitude takeover control in post-capture of target by space manipulators, J. Franklin Inst. B (ISSN: 0016-0032) 353 (9) (2016) 1985 2008.
[179] M.M. Al-Isawi, J.Z. Sasiadek, Guidance and control of a robot capturing an uncooperative space target, J. Intell. Robot. Syst. 93 (3 4) (2019) 713 721.
[180] J. Virgili-Llop, C. Zagaris, R. Zappulla, A. Bradstreet, M. Romano, Labo- ratory experiments on the capture of a tumbling object by a spacecraft manipulator system using a convex-programming-based guidance, in: AAS/AIAA Astrodynamics Specialist Conference, Stevenson, WA, 2017, pp. 21 24.
[181] E. Todorov, Optimal control theory, in: K. Doya, S. Ishii, A. Pouget, R. Rao (Eds.), Bayesian Brain: Probabilistic Approaches to Neural Coding, MIT Press, Cambridge (Massachusetts), 2006, pp. 269 298.
[182] A. Flores-Abad, L. Zhang, Z. Wei, O. Ma, Optimal capture of a tumbling object in orbit using a space manipulator, J. Intell. Robotic Syst. 86 (2) (2017) 199 211.
[183] Y. Nakamura, H. Hanafusa, Optimal redundancy control of robot manipulators, Int. J. Robot. Res. 6 (1) (1987) 32 42.
[184] F. Aghili, Pre-and post-grasping robot motion planning to capture and stabilize a tumbling/drifting free-floater with uncertain dynamics, in: International Conference on Robotics and Automation, Karlsruhe, Germany, 6-10 May 2013, IEEE, 2013, pp. 5461 5468.
[185] F. Aghili, Optimal control for robotic capturing and passivation of a tumbling satellite with unknown dynamics, in: AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii, 18 - 21 August 2008, 2008, p. 7274.
[186] Q. Zhang, L. Ji, D. Zhou, X. Wei, Nonholonomic motion planning for minimizing base disturbances of space manipulators based on multi-swarm PSO, Robotica 35 (4) (2017) 861 875.
[187] M. Wang, J. Luo, U. Walter, Trajectory planning of free-floating space robot using particle swarm optimization (PSO), Acta Astronaut. 112 (2015) 77 88.
[188] W. Xu, C. Li, X. Wang, Y. Liu, B. Liang, Y. Xu, Study on non-holonomic cartesian path planning of a free-floating space robotic system, Adv. Robot. 23 (1 2) (2009) 113 143.
[189] W. Xu, Y. Liu, B. Liang, Y. Xu, C. Li, W. Qiang, Non-holonomic path planning of a free-floating space robotic system using genetic algorithms, Adv. Robot. 22 (4) (2008) 451 476.
[190] P. Huang, K. Chen, Y. Xu, Optimal path planning for minimizing disturbance of space robot, in: 9th International Conference on Control, Automation, Robotics and Vision, Singapore, 5-8 Dec. 2006, IEEE, 2006, pp. 1 6.
[191] M. Jankovic, F. Kirchner, Trajectory generation method for robotic free-floating capture of a non-cooperative, tumbling target, in: Stardust Final Conference: Advances in Asteroids and Space Debris Engineering and Science, February 10, 2018, Springer, 2018, pp. 111 127.
[192] A. Piazzi, A. Visioli, Global minimum-jerk trajectory planning of robot manipulators, IEEE Trans. Ind. Electron. 47 (1) (2000) 140 149.
[193] C. De Silva, Trajectory design for robotic manipulators in space applications, J. Guid. Control Dyn. 14 (3) (1991) 670 674.
[194] Z. Liu, P. Huang, J. Yan, G. Liu, Multi-objective genetic algorithms for trajectory optimization of space manipulator, in: 4th Conference on Industrial Electronics and Applications, Xi an, China, 25-27 May 2009, IEEE, 2009, pp. 2810 2815.
[195] P. Huang, Y. Xu, B. Liang, Global minimum-jerk trajectory planning of space manipulator, Int. J. Control Autom. Syst. 4 (4) (2006) 405 413.
[196] P. Huang, K. Chen, J. Yuan, Y. Xu, Motion trajectory planning of space manip- ulator for joint jerk minimization, in: International Conference on Mechatronics and Automation, Harbin, China, 5-8 Aug. 2007, IEEE, 2007, pp. 3543 3548.
[197] Y. Umetani, K. Yoshida, Continuous path control of space manipulators mounted on OMV, Acta Astronaut. 15 (12) (1987) 981 986.
[198] K. Yoshida, Y. Umetani, Control of space manipulators with generalized Jacobian matrix, in: Space Robotics: Dynamics and Control, Springer, 1993, pp. 165 204.
[199] K. Yoshida, D. Dimitrov, H. Nakanishi, On the capture of tumbling satellite by a space robot, in: International Conference on Intelligent Robots and Systems, Beijing, China, 9-15 Oct. 2006, IEEE, 2006, pp. 4127 4132.
[200] D.N. Nenchev, K. Yoshida, Impact analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse, IEEE Trans. Robot. Autom. 15 (3) (1999) 548 557.
[201] K. Yoshida, Y. Umetani, Control of space free-flying robot, in: 29th Conference on Decision and Control, Honolulu, HI, USA, 5-7 Dec. 1990, IEEE, 1990, pp. 97 102.
[202] Y. Umetani, K. Yoshida, Workspace and manipulability analysis of space manipulator, Trans. Soc. Instrum. Control Eng. 26 (2) (1990) 188 195.
[203] K. Yoshida, K. Hashizume, S. Abiko, Zero reaction maneuver: Flight validation with ETS-vii space robot and extension to kinematically redundant arm, in: Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Vol. 1, IEEE, 2001, pp. 441 446.
[204] D. Nenchev, Y. Umetani, K. Yoshida, Analysis of a redundant free-flying spacecraft/manipulator system, IEEE Trans. Robot. Autom. 8 (1) (1992) 1 6. [205] O.P. Agrawal, Y. Xu, On the global optimum path planning for redundant space manipulators, IEEE Trans. Syst. Man Cybern. 24 (9) (1994) 1306 1316.
[206] Y. Taira, S. Sagara, R. Katoh, Digital adaptive control of space robot manipulators using transpose of generalized Jacobian matrix, in: Interna- tional Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No.00CH37113), Takamatsu, Japan, 31 Oct.-5 Nov. 2000, Vol. 2, 2000, pp. 1553 1558 vol.2.
[207] D.N. Nenchev, K. Yoshida, P. Vichitkulsawat, M. Uchiyama, Reaction null-space control of flexible structure mounted manipulator systems, IEEE Trans. Robot. Autom. 15 (6) (1999) 1011 1023.
[208] K. Yoshida, R. Kurazume, Y. Umetani, Dual arm coordination in space free-flying robot, in: International Conference on Robotics and Automation, Sacramento, California, 9-11 April 1991, IEEE, 1991, pp. 2516 2521.
[209] S. Dubowsky, Z. Vafa, A virtual manipulator model for space robotic systems, Technical Report, NASA, 1987.
[210] Z. Vafa, S. Dubowsky, The kinematics and dynamics of space manipulators: The virtual manipulator approach, Int. J. Robot. Res. 9 (4) (1990) 3 21.
[211] Z. Vafa, S. Dubowsky, On the dynamics of space manipulators using the virtual manipulator, with applications to path planning, in: Space Robotics: Dynamics and Control, Springer, 1993, pp. 45 76.
[212] O. Parlaktuna, M. Ozkan, Adaptive control of free-floating space manipulators using dynamically equivalent manipulator model, Robot. Auton. Syst. 46 (3) (2004) 185 193.
[213] B. Liang, Y. Xu, M. Bergerman, Mapping a space manipulator to a dynamically equivalent manipulator, J. Dyn. Syst. Meas. Control (1998).
[214] M.A. Torres, S. Dubowsky, Path-planning for elastically constrained space manipulator systems, in: International Conference on Robotics and Automation, Atlanta, GA, USA, 2-6 May 1993, IEEE, 1993, pp. 812 817.
[215] A. Madhani, S. Dubowsky, Motion planning of mobile multi-limb robotic systems subject to force and friction constraints, in: International Conference on Robotics and Automation, Nice, France, France, 12-14 May 1992, IEEE, 1992, pp. 233 239.
[216] K. Seweryn, M. Banaszkiewicz, Optimization of the trajectory of a general free-flying manipulator during the rendezvous maneuver, in: AIAA Guidance, Navigation and Control Conference and Exhibit, 2008, p. 7273.
[217] R. Mukherjee, D. Chen, Control of free-flying underactuated space manipulators to equilibrium manifolds, IEEE Trans. Robot. Autom. 9 (5) (1993) 561 570.
[218] P. Merat, F. Aghili, C.Y. Su, Modeling, control and simulation of a 6-DOF reconfigurable space manipulator with lockable cylindrical joints, in: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 8103 LNAI, (PART 2) 2013, pp. 121 131.
[219] R. Lampariello, S. Agrawal, G. Hirzinger, Optimal motion planning for free- flying robots, in: International Conference on Robotics and Automation (Cat. No. 03CH37422), Taipei, Taiwan, 14-19 Sept. 2003, 3, IEEE, 2003, pp. 3029 3035.
[220] A. Seddaoui, C.M. Saaj, Collision-free optimal trajectory for a controlled floating space robot, in: K. Althoefer, J. Konstantinova, K. Zhang (Eds.), Towards Autonomous Robotic Systems, Springer International Publishing, Cham, ISBN: 978-3-030-25332-5, 2019, pp. 248 260.
[221] K. Yamada, Attitude control of space robot by arm motion, J. Guid. Control Dyn. 17 (5) (1994) 1050 1054. [222] K. Yamada, S. Yoshikawa, Y. Fujita, Arm path planning of a space robot with angular momentum, Adv. Robot. 9 (6) (1994) 693 709.
[223] Y. Nakamura, R. Mukherjee, Nonholonomic path planning of space robots via bi-directional approach, in: International Conference on Robotics and Automation, Cincinnati, OH, USA, 13-18 May 1990, IEEE, 1990, pp. 1764 1769.
[224] V. Schulz, R. Longman, H.G. Bock, Computer-aided motion planning for satellite mounted robots, Math. Methods Appl. Sci. 21 (8) (1998) 733 755.
[225] J. Peng, W. Xu, Z. Hu, B. Liang, A. Wu, Modeling and analysis of the multiple dynamic coupling effects of a dual-arm space robotic system, Robotica 38 (6) (2020) 1 20.
[226] S.A.A. Moosavian, E. Papadopoulos, Explicit dynamics of space free-flyers with multiple manipulators via spacemaple, Adv. Robot. 18 (2) (2004) 223 244.
[227] K. Yoshida, R. Kurazume, Y. Umetani, Torque optimization control in space robots with a redundant arm, in: IROS 91. IEEE/RSJ International Workshop on Intelligent Robots and Systems, Osaka, Japan, 3-5 Nov. 1991, IEEE, 1991, pp. 1647 1652.
[228] K. Yoshida, R. Kurazume, Y. Umetani, Coordinated control of multiple manipulators in space robots, J. Robot. Soc. Japan 9 (6) (1991) 718 726.
[229] S.A.A. Moosavian, E. Papadopoulos, On the kinematics of multiple manipulator space free-flyers and their computation, J. Robot. Syst. 15 (4) (1998) 207 216.
[230] E. Papadopoulos, S.A.A. Moosavian, Dynamics and control of multi-arm space robots during chase and capture operations, in: International Conference on Intelligent Robots and Systems (IROS 94), Munich, Germany, 12-16 Sept. 1994, 3, IEEE, 1994, pp. 1554 1561.
[231] T. Tarn, A. Bejczy, X. Yun, Coordinated control of two robot arms, in: International Conference on Robotics and Automation, 7-10 April 1986, San Francisco, CA, USA, USA, 3, IEEE, 1986, pp. 1193 1202.
[232] H. Kawasaki, S. Ueki, S. Ito, Decentralized adaptive coordinated control of multiple robot arms without using a force sensor, Automatica 42 (3) (2006) 481 488.
[233] J.-H. Jean, L.-C. Fu, An adaptive control scheme for coordinated multimanipu- lator systems, IEEE Trans. Robot. Autom. 9 (2) (1993) 226 231.
[234] B. Yao, W. Gao, S. Chan, M. Cheng, VSC coordinated control of two manipulator arms in the presence of environmental constraints, IEEE Trans. Automat. Control 37 (11) (1992) 1806 1812. [235] P. Hsu, Coordinated control of multiple manipulator systems, IEEE Trans. Robot. Autom. 9 (4) (1993) 400 410.
[236] H. Zhao, C. Wang, Z. Guo, Coordinated dynamics control of a free-floating dual-arm space robot, Modern Appl. Sci. 4 (5) (2010) 175.
[237] P. Huang, Y. Xu, B. Liang, Dynamic balance control of multi-arm free-floating space robots, Int. J. Adv. Robot. Syst. 2 (2) (2005) 13.
[238] P. Huang, Y. Xu, B. Liang, Balance control of multi-arm free-floating space robots during capture operation, in: International Conference on Robotics and Biomimetics-ROBIO, 5-9 July 2005, Shatin, China, IEEE, 2005, pp. 398 403.
[239] L. Shi, S. Kayastha, J. Katupitiya, Robust coordinated control of a dual-arm space robot, Acta Astronaut. 138 (2017) 475 489.
[240] S. Hayati, Hybrid position/force control of multi-arm cooperating robots, in: International Conference on Robotics and Automation, 7-10 April 1986, San Francisco, CA, USA, USA, 3, IEEE, 1986, pp. 82 89.
[241] M. Uchiyama, P. Dauchez, Symmetric kinematic formulation and non- master/slave coordinated control of two-arm robots, Adv. Robot. 7 (4) (1992) 361 383.
[242] H. Kawasaki, S. Ito, R.B. Ramli, Adaptive decentralized coordinated control of multiple robot arms, IFAC Proc. Vol. 36 (17) (2003) 387 392.
[243] J. Zhou, X. Ding, Y.Y. Qing, Automatic planning and coordinated control for redundant dual-arm space robot system, Ind. Robot Int. J. (2011).
[244] M.W. Walker, L.-B. Wee, Adaptive control of space-based robot manipulators, IEEE Transactions on Robotics and Automation 7 (6) (1991) 828 835.
[245] H. Wang, On adaptive inverse dynamics for free-floating space manipulators, Robot. Auton. Syst. (ISSN: 0921-8890) 59 (10) (2011) 782 788.
[246] L.B. Wee, M.W. Walker, N.H. McClamroch, An articulated-body model for a free-flying robot and its use for adaptive motion control, IEEE Trans. Robot. Autom. 13 (2) (1997) 264 277.
[247] J.-F. Shi, S. Ulrich, S. Ruel, M. Anctil, Uncooperative spacecraft pose estima- tion using an infrared camera during proximity operations, in: AIAA SPACE Conference and Exposition, Pasadena, California, 31 Aug-2 Sep 2015, 2015, p. 4429.
[248] S. Ulrich, A. Saenz-Otero, I. Barkana, Passivity-based adaptive control of robotic spacecraft for proximity operations under uncertainties, J. Guid. Control Dyn. 39 (6) (2016) 1444 1453.
[249] S. Ulrich, J.Z. Sasiadek, I. Barkana, Modeling and direct adaptive control of a flexible-joint manipulator, J. Guid. Control Dyn. 35 (1) (2012) 25 39.
[250] S. Ulrich, J. Sasiadek, Direct model reference adaptive control of a flexible joint robot, in: AIAA Guidance, Navigation, and Control Conference, 2010, p. 7844.
[251] Y. Cao, C. De Silva, Dynamic modeling and neural-network adaptive control of a deployable manipulator system, J. Guid. Control Dyn. 29 (1) (2006) 192 195.
[252] S. Ulrich, J.Z. Sasiadek, Extended Kalman filtering for flexible joint space robot control, in: American Control Conference, San Francisco, CA, USA, 29 June-1 July 2011, IEEE, 2011, pp. 1021 1026.
[253] S. Ulrich, J.Z. Sasiadek, 16th International Conference on Methods & Models in Automation & Robotics, Miedzyzdroje, Poland, 22-25 Aug. 2011, IEEE, 2011, pp. 290 295.
[254] A. Green, J. Sasiadek, Adaptive control of a flexible robot using fuzzy logic, J. Guid. Control Dyn. 28 (1) (2005) 36 42.
[255] Z. Li, B. Wang, H. Liu, Target capturing control for space robots with unknown mass properties: a self-tuning method based on gyros and cameras, Sensors 16 (9) (2016) 1383.
[256] M. Shibli, C.-Y. Su, F. Aghili, Adaptive inverse dynamics control of a free-flying space robot in contact with a target satellite: A hubble space telescope case, in: Canadian Conference on Electrical and Computer Engineering, Ottawa, Ont., Canada, 7-10 May 2006, IEEE, 2006, pp. 1275 1278.
[257] D.A. Haghighi, S. Mobayen, Design of an adaptive super-twisting decoupled terminal sliding mode control scheme for a class of fourth-order systems, ISA Trans. 75 (2018) 216 225.
[258] V.I. Utkin, Variable structure systems with sliding modes, IEEE Trans. Autom. Control 22 (2) (1977) 212 222.
[259] S. Amirkhani, S. Mobayen, N. Iliaee, O. Boubaker, S.H. Hosseinnia, Fast terminal sliding mode tracking control of nonlinear uncertain mass spring system with experimental verifications, Int. J. Adv. Robot. Syst. 16 (1) (2019) 1729881419828176.
[260] Z. Lin, Q. Zhu, C. Cai, Variable structure control based on sliding mode for a 2-dof underactuated robot manipulator, in: 6th World Congress on Intelligent Control and Automation, Dalian, China, 21-23 June 2006, Vol. 1, 2006, pp. 2029 2033.
[261] H. Ashrafiuon, R.S. Erwin, Sliding mode control of underactuated multibody systems and its application to shape change control, Internat. J. Control 81 (12) (2008) 1849 1858.
[262] Y. Jia, S. Xu, Decentralized adaptive sliding mode control of a space robot actuated by control moment gyroscopes, Chin. J. Aeronaut. 29 (3) (2016) 688 703.
[263] A. Arisoy, M.K. Bayrakceken, S. Basturk, M. Gokasan, O.S. Bogosyan, High order sliding mode control of a space robot manipulator, in: Proceedings of 5th International Conference on Recent Advances in Space Technologies-RAST2011, Istanbal, Turkey, 9-11 June 2011, IEEE, 2011, pp. 833 838.
[264] A. Seddaoui, C.M. Saaj, Combined Nonlinear H infinity Controller for a Controlled-Floating Space Robot, J. Guid. Control Dyn., 1 8.
[265] K. Nanos, E.G. Papadopoulos, Control engineering practice on the dynamics and control of flexible joint space manipulators, Control Eng. Pract. 45 (2015) 230 243.
[266] M.W. Spong, Modeling and control of elastic joint robots, J. Dyn. Syst. Meas. Control 109 (4) (1987) 310 318.
[267] S. Ulrich, J.Z. Sasiadek, Methods of trajectory tracking for flexible joint space manipulators, IFAC Proc. Vol. 44 (1) (2011) 10307 10312.
[268] A. Krzyżak, J.Z. Sasiadek, S. Ulrich, Nonparametric identification of robot flexible joint space manipulator, in: 17th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdrojie, Poland, 27-30 Aug. 2012, IEEE, 2012, pp. 172 177.
[269] A. Kumar, P.M. Pathak, N. Sukavanam, Trajectory control of a two DOF rigid- flexible space robot by a virtual space vehicle, Robot. Auton. Syst. 61 (5) (2013) 473 482.
[270] J.-J. Slotine, L. Weiping, Adaptive manipulator control: A case study, IEEE Trans. Autom. Control 33 (11) (1988) 995 1003.
[271] M.W. Spong, Adaptive control of flexible joint manipulators, Systems Control Lett. 13 (1) (1989) 15 21.
[272] B. Brogliato, R. Ortega, R. Lozano, Global tracking controllers for flexible-joint manipulators: a comparative study, Automatica 31 (7) (1995) 941 956.
[273] Y. Murotsu, S. Tsujio, K. Senda, M. Hayashi, Trajectory control of flexible manipulators on a free-flying space robot, IEEE Control Syst. Mag. 12 (3) (1992) 51 57.
[274] K. Nanos, E.G. Papadopoulos, On the dynamics and control of flexible joint space manipulators, Control Eng. Pract. 45 (2015) 230 243.
[275] V. Dubanchet, Modeling and control of a flexible space robot to capture a tumbling debris (Ph.D. thesis), École Polytechnique de Montréal, 2016.
[276] R.T. Newton, Y. Xu, Neural network control of a space manipulator, IEEE Control Syst. Mag. 13 (6) (1993) 14 22.
[277] C. Li, Adaptive and robust composite control of coordinated motion of space robot system with prismatic joint, in: Proceedings of the 4th World Congress on Intelligent Control and Automation (Cat. No. 02EX527), Vol. 2, IEEE, 2002, pp. 1255 1259.
[278] M. Dor, P. Tsiotras, ORB-SLAM applied to spacecraft non-cooperative ren- dezvous, in: Space Flight Mechanics Meeting, Kissimmee, Florida, 8 12 January 2018, 2018, p. 1963.
[279] S. Abiko, K. Yoshida, Adaptive reaction control for space robotic applications with dynamic model uncertainty, Adv. Robot. 24 (8 9) (2010) 1099 1126.
[280] R. Johansson, Quadratic optimization of motion coordination and control, IEEE Trans. Autom. Control 35 (11) (1990) 1197 1208.
[281] C.-D. Yang, C.-C. Kung, Nonlinear h 8 flight control of general six-degree-of- freedom motions, J. Guid. Control Dyn. 23 (2) (2000) 278 288.
[282] H.-J. Uang, C.-C. Lien, Mixed H2/h infinity PID tracking control design for uncertain spacecraft systems using a cerebellar model articulation controller, IEEE Proc. D 153 (1) (2006) 1 13.
[283] S. Ozgoli, H. Taghirad, Designing and implementation of mixed 퐻 2 /퐻 controller for flexible joint robot to encounter actuator saturation, 2006, Accessed: 27.05.2020, URL: https://aras.kntu.ac.ir/wp-content/uploads/2019/ 07/2006_ICEE_C_FR.pdf.
[284] A. Mohamed, C. Saaj, A. Seddaoui, S. Eckersley, et al., Controlling a non-linear space robot using linear controllers, in: 5th CEAS Conference on Guidance, Navigation and Control (EuroGNC), April 3-5, 2019, Milan, Italy, 2019.
[285] A.A. Siqueira, M.H. Terra, J.Y. Ishihara, T.L. Barbeiro, Underactuated ma- nipulator robot control via 퐻 2 , 퐻 , 퐻 2 /퐻 , and 휇 -synthesis approaches: a comparative study, J. Guidance Control Dyn. 31 (4) (2009) 279 288.
[286] C.J. Lee, C. Mavroidis, Discrete-time LQR and 퐻 2 damping control of flexible payloads using a robot manipulator with a wrist-mounted force/torque sensor, J. Dyn. Syst. Meas. Control (2000).
[287] V. Dubanchet, D. Saussié, D. Alazard, C. Bérard, C. Le Peuvédic, Modeling and control of a space robot for active debris removal, CEAS Space J. 7 (2) (2015) 203 218.
[288] D.N. Nenchev, K. Yoshida, Impact analysis and post-impact motion control issues of a free-floating space robot contacting a tumbling object, in: Interna- tional Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, Belgium, 20-20 May 1998, 1, IEEE, 1998, pp. 913 919.
[289] T.-C. Nguyen-Huynh, I. Sharf, Adaptive reactionless motion for space manipu- lator when capturing an unknown tumbling target, in: International Conference on Robotics and Automation, Shanghai, China, 9-13 May 2011, IEEE, 2011, pp. 4202 4207.
[290] S.-I. Nishida, T. Yoshikawa, Capture and motion braking of space debris by a space robot, in: International Conference on Control, Automation and Systems, Seoul, South Korea, 17-20 Oct. 2007, 2007, pp. 706 711.
[291] S. Nishida, T. Yoshikawa, Space debris capture by a joint compliance controlled robot, in: International Conference on Advanced Intelligent Mechatronics, Kobe, Japan, 20-24 July 2003, 1, 2003, pp. 496 502 vol.1.
[292] D. Hirano, H. Kato, T. Saito, Online path planning and compliance control of space robot for capturing tumbling large object, in: 2018 IEEE/RSJ Interna- tional Conference on Intelligent Robots and Systems (IROS), IEEE, 2018, pp. 2909 2916.
[293] N. Uyama, D. Hirano, H. Nakanishi, K. Nagaoka, K. Yoshida, Impedance- based contact control of a free-flying space robot with respect to coefficient of restitution, in: 2011 IEEE/SICE International Symposium on System Integration (SII), IEEE, 2011, pp. 1196 1201.
[294] N. Uyama, H. Nakanishi, K. Nagaoka, K. Yoshida, Impedance-based contact control of a free-flying space robot with a compliant wrist for non-cooperative satellite capture, in: International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7-12 Oct. 2012, 2012, pp. 4477 4482.
[295] P. Palma, K. Seweryn, Space robot equipped with compliant linear actuator on end effector: simulations results, in: Photonics Applications in Astronomy, Com- munications, Industry, and High-Energy Physics Experiments, Wilga, Poland, 6 November2019, 11176, International Society for Optics and Photonics, 2019, p. 111763H.
[296] S.A.A. Moosavian, R. Rastegari, E. Papadopoulos, Multiple impedance control for space free-flying robots, J. Guid. Control Dyn. 28 (5) (2005) 939 947.
[297] P. Boning, S. Dubowsky, Coordinated control of space robot teams for the on- orbit construction of large flexible space structures, Adv. Robot. 24 (3) (2010) 303 323.
[298] F. Aghili, Optimal trajectories and robot control for detumbling a non-cooperative satellite, J. Guid. Control Dyn. 43 (5) (2020) 981 988.
[299] A. Nanjangud, P. Blacker, S. Bandyopadhyay, Y. Gao, Robotics and AI-enabled on-orbit operations with future generation of small satellites, Proc. IEEE 106 (3) (2018) 429 439.
[300] J.A. Perez, F. Deligianni, D. Ravi, G.-Z. Yang, Artificial intelligence and robotics, 2018, arXiv preprint arXiv:1803.10813.
[301] D. Ernst, M. Glavic, F. Capitanescu, L. Wehenkel, Reinforcement learning versus model predictive control: a comparison on a power system problem, IEEE Trans. Syst. Man Cybern. Part B 39 (2) (2008) 517 529.
[302] C.-J. Lin, C.-T. Lin, An ART-based fuzzy adaptive learning control network, IEEE Trans. Fuzzy Syst. 5 (4) (1997) 477 496.
[303] C.J. Ostafew, A.P. Schoellig, T.D. Barfoot, Learning-based nonlinear model predictive control to improve vision-based mobile robot path-tracking in chal- lenging outdoor environments, in: International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May-7 June 2014, IEEE, 2014, pp. 4029 4036.
[304] S. Gu, E. Holly, T. LillICRAp, S. Levine, Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates, in: International Conference on Robotics and Automation (ICRA), Singapore, 29 May-3 June 2017, IEEE, 2017, pp. 3389 3396.
[305] K. Lowrey, S. Kolev, J. Dao, A. Rajeswaran, E. Todorov, Reinforcement learning for non-prehensile manipulation: Transfer from simulation to physical system, in: International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), Brisbane, QLD, Australia, 16-19 May 2018, IEEE, 2018, pp. 35 42.
[306] F. Stulp, E.A. Theodorou, S. Schaal, Reinforcement learning with sequences of motion primitives for robust manipulation, IEEE Trans. Robotics 28 (6) (2012) 1360 1370.
[307] A.S. Polydoros, L. Nalpantidis, Survey of model-based reinforcement learning: Applications on robotics, J. Intell. Robotic Syst. 86 (2) (2017) 153 173. [308] S. Bhasin, Reinforcement learning and optimal control methods for uncertain nonlinear systems, University of Florida, 2011.
[309] K. Senda, T. Matsumoto, Y. Okano, S. Mano, S. Fujii, Autonomous task achievement by space robot based on q-learning with environment recognition, in: AIAA Guidance, Navigation, and Control Conference and Exhibit, 2003, p. 5426.
[310] J. Kober, J.A. Bagnell, J. Peters, Reinforcement learning in robotics: A survey, Int. J. Robot. Res. 32 (11) (2013) 1238 1274. [311] J. Mahler, M. Matl, V. Satish, M. Danielczuk, B. DeRose, S. McKinley, K. Goldberg, Learning ambidextrous robot grasping policies, 2019, p. 4.
[312] J.-J. Park, J.-H. Kim, J.-B. Song, Path planning for a robot manipulator based on probabilistic roadmap and reinforcement learning, Int. J. Control Autom. Syst. 5 (6) (2007) 674 680.
[313] A. Faust, K. Oslund, O. Ramirez, A. Francis, L. Tapia, M. Fiser, J. Davidson, PRM-RL: Long-range robotic navigation tasks by combining reinforcement learning and sampling-based planning, in: International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21-25 May 2018, IEEE, 2018, pp. 5113 5120.
[314] M. Han, B. Zhang, Control of robotic manipulators using a CMAC-based reinforcement learning system, in: Proceedings of International Conference on Intelligent Robots and Systems (IROS 94), Munich, Germany, 12-16 Sept. 1994, 3, IEEE, 1994, pp. 2117 2122.
[315] Y.H. Kim, F.L. Lewis, Optimal design of CMAC neural-network controller for robot manipulators, IEEE Trans. Syst. Man Cybern. Part C 30 (1) (2000) 22 31.
[316] T.P. Lillicrap, J.J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, D. Wierstra, Continuous control with deep reinforcement learning, 2015, arXiv preprint arXiv:1509.02971.
[317] Z. Miljković, M. Mitić, M. Lazarević, B. Babić, Neural network reinforcement learning for visual control of robot manipulators, Expert Syst. Appl. 40 (5) (2013) 1721 1736.
[318] Y. Zhang, N. Fattahi, W. Li, Probabilistic roadmap with self-learning for path planning of a mobile robot in a dynamic and unstructured environment, in: International Conference on Mechatronics and Automation, Takamatsu, Japan, 4-7 Aug. 2013, IEEE, 2013, pp. 1074 1079.
[319] D. Baek, M. Hwang, H. Kim, D.-S. Kwon, Path planning for automation of surgery robot based on probabilistic roadmap and reinforcement learning, in: 15th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 26-30 June 2018, IEEE, 2018, pp. 342 347.
[320] R.S. Sutton, A.G. Barto, et al., Introduction to reinforcement learning, Vol. 135, MIT press Cambridge, 1998.
[321] E. Talvitie, Agnostic system identification for monte carlo planning, in: Twenty-Ninth AAAI Conference on Artificial Intelligence, 2015. [322] S. Ross, J.A. Bagnell, Agnostic system identification for model-based reinforcement learning, 2012, arXiv preprint arXiv:1203.1007.
[323] F.L. Lewis, D. Vrabie, K.G. Vamvoudakis, Reinforcement learning and feedback control: Using natural decision methods to design optimal adaptive controllers, IEEE Control Syst. Mag. 32 (6) (2012) 76 105.
[324] K.-S. Hwang, S.-W. Tan, M.-C. Tsai, Reinforcement learning to adaptive control of nonlinear systems, IEEE Trans. Syst. Man Cybern. Part B 33 (3) (2003) 514 521.
[325] J.F. Fisac, A.K. Akametalu, M.N. Zeilinger, S. Kaynama, J. Gillula, C.J. Tomlin, A general safety framework for learning-based control in uncertain robotic systems, IEEE Trans. Autom. Control (2018).
[326] Y.P. Pane, S.P. Nageshrao, R. Babuška, Actor-critic reinforcement learning for tracking control in robotics, in: 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12-14 Dec. 2016, IEEE, 2016, pp. 5819 5826.
[327] S. Gu, E. Holly, T. LillICRAp, S. Levine, Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates, in: International Conference on Robotics and Automation (ICRA), Singapore, 29 May-3 June 2017, IEEE, 2017, pp. 3389 3396.
[328] T. Kondo, K. Ito, A reinforcement learning with evolutionary state recruitment strategy for autonomous mobile robots control, Robot. Auton. Syst. 46 (2) (2004) 111 124.
[329] S.P. Gadanho, Reinforcement learning in autonomous robots: An empirical investigation of the role of emotions (Ph.D. thesis), University of Edinburgh. College of Science and Engineering., 1999.
[330] C.J. Ostafew, A.P. Schoellig, T.D. Barfoot, J. Collier, Learning-based nonlinear model predictive control to improve vision-based mobile robot path tracking, J. Field Robotics 33 (1) (2016) 133 152.
[331] P. Mihelich, Motion planning for the ATHLETE rover with reinforcement learning, 2008, Unpublished manuscript. [332] D.S. Bernstein, S. Zilberstein, Reinforcement learning for weakly-coupled MDPs and an application to planetary rover control, in: Sixth European Conference on Planning, Toledo, Spain, September 1, 2013, 2014, pp. 240 243.
[333] R. Cui, C. Yang, Y. Li, S. Sharma, Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning, IEEE Trans. Syst. Man Cybern. Syst. 47 (6) (2017) 1019 1029.
[334] C.-K. Lin, H infinity reinforcement learning control of robot manipulators using fuzzy wavelet networks, Fuzzy Sets and Systems 160 (12) (2009) 1765 1786.
[335] I. Eski, S. Erkaya, S. Savas, S. Yildirim, Fault detection on robot manipulators using artificial neural networks, Robot. Comput.-Integr. Manuf. 27 (1) (2011) 115 123.
[336] S.K. Pradhan, B. Subudhi, Real-time adaptive control of a flexible manipulator using reinforcement learning, IEEE Trans. Autom. Sci. Eng. 9 (2) (2012) 237 249.
[337] L. Tang, Y.-J. Liu, S. Tong, Adaptive neural control using reinforcement learning for a class of robot manipulator, Neural Comput. Appl. 25 (1) (2014) 135 141.
[338] C. Macnab, G.M. D Eleuterio, Stable, online learning using CMACs for neu- roadaptive tracking control of flexible-joint manipulators, in: International Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, Belgium, 20-20 May 1998, 1, IEEE, 1998, pp. 511 517.
[339] C.-K. Lin, A reinforcement learning adaptive fuzzy controller for robots, Fuzzy Sets and Systems 137 (3) (2003) 339 352.
[340] B. Subudhi, S.K. Pradhan, Direct adaptive control of a flexible robot using reinforcement learning, in: International Conference on Industrial Electronics, Control and Robotics, Orissa, India, 27-29 Dec. 2010, IEEE, 2010, pp. 129 136.
[341] A. Muller, Z. Terze, Geometric methods and formulations in computational multibody system dynamics, Acta Mech. 227 (12) (2015) 3327 3350.
[342] J. Marsden, A. Weinstein, Reduction of symplectic manifolds with symmetry, Rep. Math. Phys. (ISSN: 0034-4877) 5 (1) (1974) 121 130.
[343] K.R. Meyer, Symmetries and integrals in mechanics, in: Dynamical Systems, Elsevier, 1973, pp. 259 272.
[344] S.P. Viswanathan, A.K. Sanyal, E. Samiei, Integrated guidance and feedback control of underactuated robotics system in se(3), J. Intell. Robotic Syst. (ISSN: 1573-0409) 89 (1) (2018) 251 263.
[345] A.M. Bloch, P.S. Krishnaprasad, J.E. Marsden, R.M. Murray, Nonholonomic mechanical systems with symmetry, Arch. Ration. Mech. Anal. 136 (1) (1996) 21 99.
[346] A.M. Bloch, T.S. Ratiu, J. Scheurle, Applied dynamics and geometric mechanics, Oberwolfach Rep. 8 (3) (2012) 2217 2282.
[347] W. Xu, B. Liang, C. Li, Y. Xu, Autonomous rendezvous and robotic capturing of non-cooperative target in space, Robotica 28 (5) (2010) 705 718.
[348] C.A. Avizzano, A. Filippeschi, J.M.J. Villegas, E. Ruffaldi, An optimal geometric model for clavels delta robot, in: European Modelling Symposium (EMS), Madrid, Spain, 6-8 Oct. 2015, IEEE, 2015, pp. 232 237.
[349] J. Hrdina, A. Návrat, P. Vašík, R. Matoušek, Geometric control of the trident snake robot based on CGA, Adv. Appl. Clifford Algeb. (ISSN: 1661-4909) 27 (1) (2017) 633 645.
[350] V. Muralidharan, A.D. Mahindrakar, Geometric controllability and stabilization of spherical robot dynamics, IEEE Trans. Autom. Control 60 (10) (2015) 2762 2767.
[351] H.E. Taha, C.A. Woolsey, Geometric control of a flapping plate, JVC/J. Vib. Control 21 (11) (2015) 2124 2133.
[352] D. Prattichizzo, P. Mercorelli, Geometric control tools for robotic manipulators, in: European Control Conference (ECC), Karlsruhe, Germany, 31 Aug.-3 Sept. 1999, IEEE, 1999, pp. 3298 3303.
[353] T. Hoang, L. Hieu, N.-H. Nguyen, Application and simulation of the nonlinear geometric control for quadrotor uavs, 2018.
[354] W.-S. Koon, J.E. Marsden, Optimal control for holonomic and nonholonomic mechanical systems with symmetry and Lagrangian reduction, SIAM J. Control Optim. 35 (3) (1997) 901 929.
[355] D.S. Djukic, B. Vujanovic, Noether s theory in classical nonconservative mechanics, Acta Mech. 23 (1 2) (1975) 17 27.
[356] G. Rega, H. Troger, Dimension reduction of dynamical systems: Methods, models, applications, Nonlinear Dynam. 41 (1 3) (2005) 1 15.
[357] R. Chhabra, M.R. Emami, Nonholonomic dynamical reduction of open-chain multi-body systems: A geometric approach, Mech. Mach. Theory 82 (2014) 231 255.
[358] R. Chhabra, M. Reza Emami, Y. Karshon, Reduction of hamiltonian mechanical systems with affine constraints: A geometric unification, J. Comput. Nonlinear Dyn. (ISSN: 1555-1415) 12 (2) (2016) 021007.
[359] E.J. Routh, A Treatise on the Dynamics of a System of Rigid Bodies. with Numerous Examples: The Elementary Part, Macmillan, 1882.
[360] J.E. Marsden, Lectures on Mechanics, Cambridge University Press, 1992.
[361] J.E. Marsden, T.S. Ratiu, Introduction to Mechanics and Symmetry, Springer-Verlag, New York, 1999.
[362] A.M. Bloch, Nonholonomic mechanics and control, New York: Springer, 2003.
[363] W. Koon, J.E. Marsden, Poisson reduction for nonholonomic mechanical systems with symmetry, Rep. Math. Phys. 42 (1998) 101 134.
[364] H. Cendra, J.E. Marsden, T.S. Ratiu, Lagrangian Reduction by Stages, Vol. 722, American Mathematical Society, 2001.
[365] J.E. Marsden, J. Scheurle, The reduced Euler-Lagrange equations, Fields Inst. Commun. 1 (1993) 139 164.
[366] J.E. Marsden, J. Scheurle, Lagrangian reduction and the double spherical pendulum, Z. Ang. Math. Phys. 44 (1993) 17 43.
[367] S. Chaplygin, On the theory of motion of nonholonomic systems. The reducing- multiplier theorem, Regul. Chaotic Dyn. 13 (4) (2008) 369 376, English translation of Matematicheskii sbornik, 1911, vol. 28, issue 1.
[368] J. Koiller, Reduction of some classical non-holonomic systems with symmetry, Arch. Ration. Mech. Anal. 118 (2) (1992) 113 148.
[369] A. van der Schaft, B.M. Maschke, On the hamiltonian formulation of nonholonomic mechanical systems, Rep. Math. Phys. 34 (2) (1994) 225 233.
[370] L. Bates, J. Śniatycki, Nonholonomic reduction, Rep. Math. Phys. 32 (1) (1993) 99 115.
[371] F. Gay-Balmaz, H. Yoshimura, Dirac reduction for nonholonomic mechanical systems and semidirect products, Advances in Applied Mathematics 63 (2015) 131 213.
[372] T. Ohsawa, O.E. Fernandez, A.M. Bloch, D.V. Zenkov, Nonholonomic hamilton- Jacobi theory via Chaplygin hamiltonization, J. Geom. Phys. 61 (8) (2011) 1263 1291.
[373] N. Sreenath, Nonlinear control of multibody systems in shape space, in: International Conference on Robotics and Automation, Cincinnati, OH, USA, 13-18 May 1990, IEEE, 1990, pp. 1776 1781.
[374] N. Sreenath, Nonlinear control of planar multibody systems in shape space, Math. Control Signals Systems 5 (4) (1992) 343 363.
[375] C.-K. Chen, Nonholonomic control of coupled spatial multibody systems (Ph.D. thesis), Case Western Reserve University, 1993.
[376] W.S. Koon, Reduction, reconstruction and optimal control of nonholonomic mechanical systems with symmetry (Ph.D. thesis), University of California, Berkeley, 1997.
[377] J. Shen, N.H. McClamroch, A.M. Bloch, Local equilibrium controllability of multibody systems controlled via shape change, IEEE Trans. Autom. Control 49 (4) (2004) 506 520.
[378] S. Jinglai, N.H. McClamroch, Translational and rotational maneuvers of an underactuated space robot using prismatic actuators, Int. J. Robot. Res. 21 (5 6) (2003) 607 618.
[379] J. Shen, Nonlinear control of multibody systems with symmetries via shape change (Ph.D. thesis), University of Michigan, 2002.
[380] J. Shen, D.A. Schneider, A.M. Bloch, Controllability and motion planning of a multibody Chaplygin s sphere and Chaplygin s top, Internat. J. Robust Nonlinear Control (ISSN: 10498923) 18 (9) (2008) 905 945.
[381] R. Shu, A. Siravuru, A. Rai, T. Dear, K. Sreenath, H. Choset, Optimal control for geometric motion planning of a robot diver, in: International Conference on Intelligent Robots and Systems (IROS), Daejeon, South Korea, 9-14 Oct. 2016, 2016, pp. 4780 4785.
[382] J. Cortés, S. Martínez, J.P. Ostrowski, H. Zhang, Simple mechanical control systems with constraints and symmetry, SIAM J. Control Optim. 41 (3) (2003) 851 874.
[383] Y. Wang, H. Hong, S. Tang, Geometric control with model predictive static programming on SO(3), Acta Astronaut. 159 (November 2018) (2019) 471 479.
[384] I.I. Hussein, A.M. Bloch, Optimal control of underactuated nonholonomic mechanical systems, IEEE Trans. Autom. Control 53 (3) (2008) 668 682.
[385] I. Hussein, A. Bloch, Constrained optimal trajectory tracking on the group of rigid body motions, in: 44th Conference on Decision and Control, Seville, Spain, 15 Dec. 2005, IEEE, 2005, pp. 2152 2157.
[386] E.A. Shammas, H. Choset, A.A. Rizzi, Towards a unified approach to motion planning for dynamic underactuated mechanical systems with non-holonomic constraints, Int. J. Robot. Res. 26 (10) (2007) 1075 1124.
[387] E.A. Shammas, H. Choset, A.A. Rizzi, Geometric motion planning analysis for two classes of underactuated mechanical systems, Int. J. Robot. Res. 26 (10) (2007) 1043 1073.
[388] X. Meng, N. Ratliff, Y. Xiang, D. Fox, Neural autonomous navigation with riemannian motion policy, in: International Conference on Robotics and Au- tomation (ICRA), Montreal, QC, Canada, Canada, 20-24 May 2019, IEEE, 2019, pp. 8860 8866.
[389] A. Isidori, Nonlinear control systems, Berlin: Springer, 1996. [390] A.A. Agrachev, Y. Sachkov, Control theory from the geometric viewpoint, Vol. 87, Springer Science & Business Media, 2013.
[391] J. Shen, D.A. Schneider, A.M. Bloch, Controllability and motion planning of multibody systems with nonholonomic constraints, in: 42nd International Conference on Decision and Control (Cat. No. 03CH37475), Maui, HI, USA, 9-12 Dec. 2003, 5, IEEE, 2003, pp. 4369 4374.
[392] M. Tayefi, Z. Geng, Self-balancing controlled Lagrangian and geometric control of unmanned mobile robots, J. Intell. Robot. Syst., Theory Appl. 90 (1 2) (2018) 253 265.
[393] J.M. Maruskin, A.M. Bloch, The Boltzmann Hamel equations for the optimal control of mechanical systems with nonholonomic constraints, Internat. J. Robust Nonlinear Control 21 (4) (2011) 373 386.
[394] J.M. Maruskin, A.M. Bloch, The Boltzmann-hamel equations for optimal control, in: 46th Conference on Decision and Control, New Orleans, la, USA, 12-14 Dec. 2007, IEEE, 2007, pp. 554 559.
[395] V. Duindam, S. Stramigioli, Singularity-free dynamic equations of open-chain mechanisms with general holonomic and nonholonomic joints, IEEE Transa. Robotics (ISSN: 1552-3098) 24 (3) (2008) 517 526.
[396] R. Olfati-Saber, Nonlinear control of underactuated mechanical systems with application to robotics and aerospace vehicles (Ph.D. thesis), Massachusetts Institute of Technology, 2001.
[397] R. Olfati-Saber, Normal forms for underactuated mechanical systems with symmetry, IEEE Trans. Autom. Control 47 (2) (2002) 305 308.
[398] J.W. Grizzle, C.H. Moog, C. Chevallereau, Nonlinear control of mechanical systems with an unactuated cyclic variable, IEEE Trans. Autom. Control 50 (5) (2005) 559 576.
[399] R. Chhabra, M.R. Emami, Symplectic reduction of holonomic open-chain multi-body systems with constant momentum, J. Geom. Phys. 89 (2015) 82 110.
[400] R. Chhabra, M.R. Emami, A unified approach to input-output linearization and concurrent control of underactuated open-chain multi-body systems with holo- nomic and nonholonomic constraints, J. Dyn. Control Syst. (ISSN: 1573-8698) 22 (1) (2016) 129 168.
[401] M. Khadem, C. Rossa, N. Usmani, R.S. Sloboda, M. Tavakoli, Geometric control of 3D needle steering in soft-tissue, Automatica 101 (December) (2019) 36 43.
[402] S. Martınez, J. Cortés, Geometric control of robotic locomotion systems, in: X Fall Workshop on Geometry and Physics, Madrid, Spain, 27 29 September 2001, RSME, 2001.
[403] S. Tashakori, G. Vossoughi, E.A. Yazdi, Geometric control of the brachiation robot using controlled Lagrangians method, in: Second RSI/ISM International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 15-17 Oct. 2014, IEEE, 2014, pp. 706 710.
[404] J. Hrdina, Local controllability of trident snake robot based on sub-Riemannian extremals, Note Matematica 37 (supp1) (2017) 93 102.
[405] D. Hirano, K. Nagaoka, K. Yoshida, Design of underactuated hand for caging- based grasping of free-flying object, in: Proceedings of the 2013 IEEE/SICE International Symposium on System Integration, IEEE, 2013, pp. 436 442.
[406] D. Kim, Y. Maeda, S. Komiyama, Caging-based grasping of deformable objects for geometry-based robotic manipulation, ROBOMECH J. (ISSN: 2197-4225) 6 (1) (2019) 3.
[407] J. Hrdina, A. Návrat, P. Vašík, R. Matoušek, CGA-Based robotic snake control, Adv. Appl. Clifford Alge. 27 (1) (2017) 621 632.
[408] A. Návrat, R. Matoušek, Trident snake control based on conformal geometric algebra, in: R. Matoušek (Ed.), Mendel 2015, Springer International Publishing, Cham, 2015, pp. 375 385.
[409] X. Guo, W. Zhu, Y. Fang, Guided motion planning for snake-like robots based on geometry mechanics and HJB equation, IEEE Trans. Ind. Electron. 66 (9) (2019) 7120 7130.
[410] X. Zhang, J. Liu, J. Feng, Y. Liu, Z. Ju, Effective capture of non-graspable objects for space robots using geometric cage pairs, IEEE/ASME Trans. Mech. (2019).
[411] H. Yoon, P. Tsiotras, Adaptive spacecraft attitude tracking control with actuator uncertainties, J. Astron. Sci. 56 (2) (2008) 251 268.
[412] Q. Hu, B. Xiao, D. Wang, E.K. Poh, Attitude control of spacecraft with actuator uncertainty, J. Guid. Control Dyn. 36 (6) (2013) 1771 1776.
[413] P. Singla, K. Subbarao, J.L. Junkins, Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty, J. Guid. Control Dyn. 29 (4) (2006) 892 902.
[414] C.L. Foster, M.L. Tinker, G.S. Nurre, W.A. Till, Solar-array-induced disturbance of the hubble space telescope pointing system, J. Spacecr. Rockets 32 (4) (1995) 634 644.
[415] R. Funase, Y. Shirasawa, Y. Mimasu, O. Mori, Y. Tsuda, T. Saiki, J. Kawaguchi, On-orbit verification of fuel-free attitude control system for spinning solar sail utilizing solar radiation pressure, Adv. Space Res. 48 (11) (2011) 1740 1746.
[416] M. Ziebart, Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape, J. Spacecraft Rockets 41 (5) (2004) 840 848.
[417] R. Kristiansen, P.J. Nicklasson, Satellite attitude control by quaternion-based backstepping, in: American Control Conference, Portland, OR, USA, 8-10 June 2005, IEEE, 2005, pp. 907 912.
[418] R.A. Phinney, R. Burridge, Representation of the elastic-gravitational excitation of a spherical earth model by generalized spherical harmonics, Geophys. J. Int. 34 (4) (1973) 451 487.
[419] R. Rummel, O. Colombo, Gravity field determination from satellite gradiometry, Bull. Géodésique 59 (3) (1985) 233 246.
[420] S.-I. Nishida, S. Kawamoto, Y. Okawa, F. Terui, S. Kitamura, Space debris removal system using a small satellite, Acta Astronaut. 65 (1 2) (2009) 95 102.
[421] G. Prölss, Magnetic storm associated perturbations of the upper atmosphere: Recent results obtained by satellite-borne gas analyzers, Rev. Geophys. 18 (1) (1980) 183 202.
[422] R.A. Langel, W.J. Hinze, The magnetic field of the Earth s lithosphere: The satellite perspective, Cambridge University Press, 1998.
[423] H. Hakima, M.R. Emami, Attitude estimation for a deorbiter cubesat, in: 9th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, Turkey, 11-14 June 2019, 2019, pp. 709 714.
[424] S. Kochetkov, Y. Rassadin, V. Utkin, Disturbance rejection in the tracking problem for robot-manipulators, in: International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21-23 June 2017, IEEE, 2017, pp. 301 306.
[425] D. Wenjie, W. Dayi, L. Chengrui, Integral sliding mode fault-tolerant control for spacecraft with uncertainties and saturation, Asian J. Control 19 (1) (2017) 372 381.
[426] M. Malekzadeh, A. Naghash, H.A. Talebi, A robust nonlinear control approach for tip position tracking of flexible spacecraft, IEEE Trans. Aerospace Electron. Syst. 47 (4) (2011) 2423 2434.
[427] M. Malekzadeh, A. Naghash, H. Talebi, Robust attitude and vibration control of a nonlinear flexible spacecraft, Asian J. Control 14 (2) (2012) 553 563.




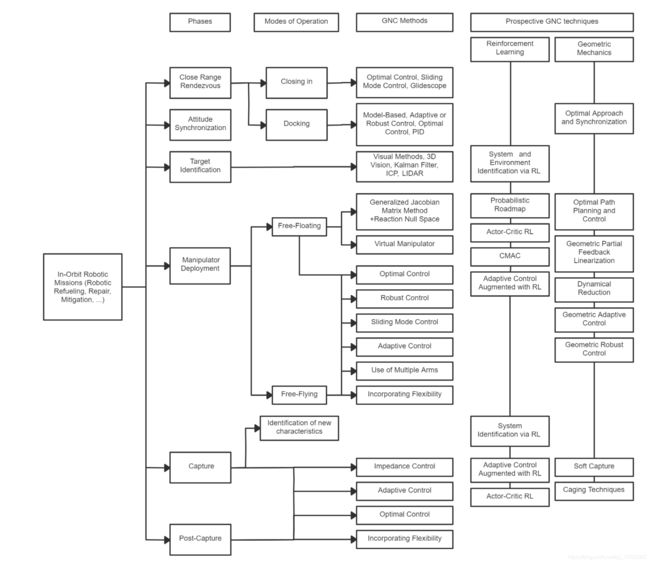
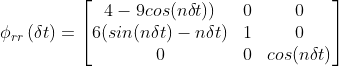
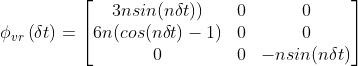
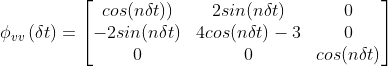
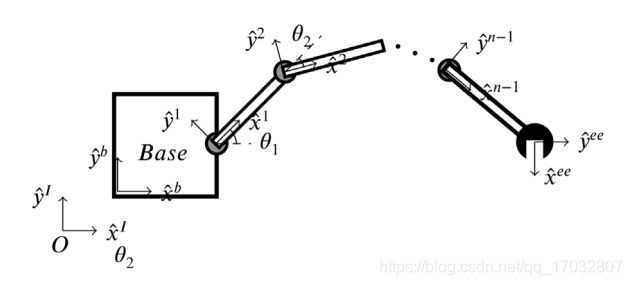
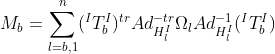
![\left [M_{bm} \right ]_j = \sum_{l=b,1}^{n} (^{I}T_{b}^{I})^{tr} Ad_{H_{l}^{I}}^{-tr} \Omega_{l} Ad_{H_{l}^{I}}^{-1}(^{I}T_{j}^{I})](http://img.e-com-net.com/image/info8/d1d5359b36c14110942586f4680dd642.gif)
![\left [M_{m} \right ]_{ij} = \sum_{l=1}^{n} (^{I}T_{i}^{I})^{tr} Ad_{H_{l}^{I}}^{-tr} \Omega_{l} Ad_{H_{l}^{I}}^{-1}(^{I}T_{j}^{I})](http://img.e-com-net.com/image/info8/31e50e51bdcc43fb80e056203a77a9d3.gif)