pytorch_lesson5 基本优化思想与最小二乘法— 建模思路+最小二乘法(最小二乘法代数表示方法+手动实现最小二乘法+lstsq最小二乘法)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、简单线性回归的机器学习建模思路
-
- 1、回顾简单线性回归建模问题
- 2.转化为优化问题
- 3.最优化问题的求解方法
-
- 图形展示目标函数
- 函数的凹凸性
- 凸函数的最小值
- SSE最小值
- 4.机器学习建模一般流程
-
- Step 1:提出基本模型
- Step 2:确定损失函数和目标函数
- Step 3:根据目标函数特性,选择优化方法,求解目标函数
- 二、第一个优化算法:最小二乘法
-
- 1.最小二乘法的代数表示方法
- 2.手动代码验证最小二乘法
- 3.lstsq实现最小二乘法
- 4.反向验证导数为零
前言
所谓优化思想,指的是利用数学工具求解复杂问题的基本思想,同时也是近现代机器学习算法在实际建模过程中经常使用基础理论在实际建模过程中,我们往往会先给出待解决问题的数值评估指标,并在此基础之上构建方程、采用数学工具、不断优化评估指标结果,以期达到可以达到的最优结果。本节,我们将先从简单线性回归入手,探讨如何将机器学习建模问题转化为最优化问题,然后考虑使用数学方法对其进行求解。
一、简单线性回归的机器学习建模思路
1、回顾简单线性回归建模问题
import numpy as np
import torch
import matplotlib as mpl
import matplotlib.pyplot as plt
A = torch.arange(1, 5).reshape(2, 2).float()
print(A)
'''
tensor([[1., 2.],
[3., 4.]])
'''
#绘制点图查看两个点的位置
plt.plot(A[:, 0], A[:, 1], 'o')
plt.show()
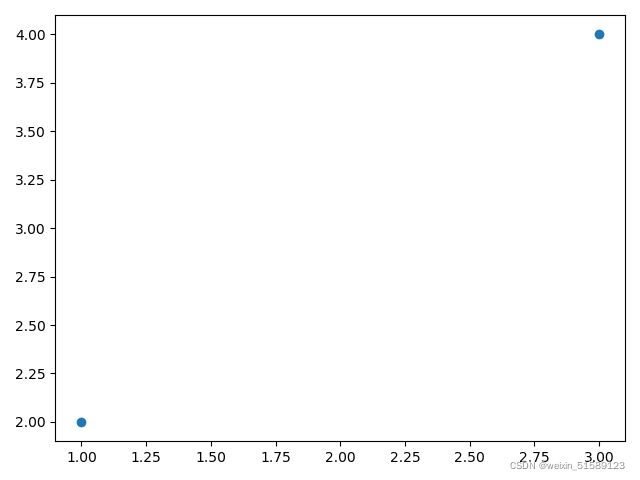
如果更进一步,我们希望在二维空间中找到一条直线,来拟合这两个点,也就是所谓的构建一个线性回归模型,我们可以设置线性回归方程如下:
2.转化为优化问题
如果我们希望通过一条直线拟合二维平面空间上分布的点,最核心的目标,毫无疑问,就是希望方程的预测值和真实值相差较小。假设真实的y值用y表示,预测值用ŷ表示,带入a、b参数,则有数值表示如下:
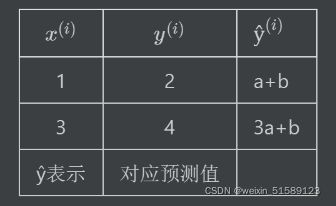
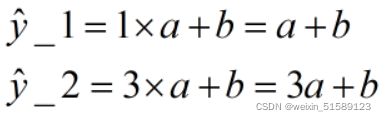
这两个预测值与真实值相差值为:

上式也就是两个点的预测值和真实值的差值的平方和,也就是所谓的,误差平方和——SSE(Sum of the Squared Errors)。
至此,我们已经将原问题转化为了一个最优化问题,接下来我们的问题就是,当a、b取何值时,SSE取值最小?值得注意的是,SSE方程就是我们优化的目标方程(求最小值),因此上述方程也被称为目标函数,同时,SSE代表着真实值和预测值之间的差值(误差平方和),因此也被称为损失函数(预测值距真实值的损失)。
3.最优化问题的求解方法
图形展示目标函数
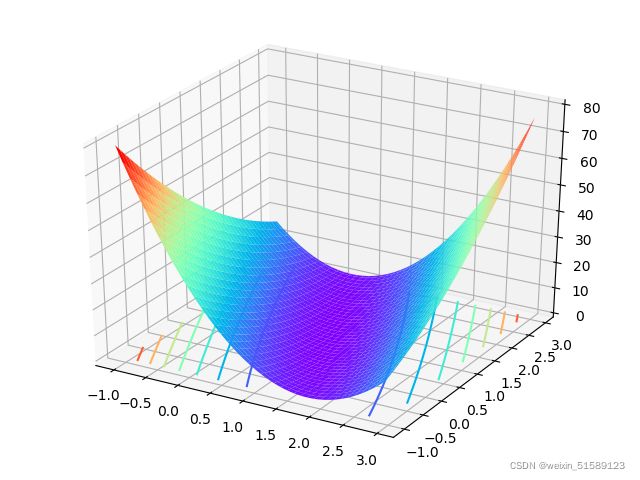
为了更好的讨论目标函数(SSE)求最小值的过程,对于上述二元函数来说,我们可以将其展示在三维空间内。此处我们可以使用Python中matplotlib包和Axes3D函数进行三维图像绘制
x = np.arange(-1, 3, 0.05)
y = np.arange(-1, 3, 0.05)
a, b = np.meshgrid(x, y)
sse = (2 - a - b) ** 2 + (4 - 3 * a - b) ** 2
ax =plt.axes(projection='3d')
ax.plot_surface(a, b, sse, cmap='rainbow')
ax.contour(a, b, sse, zdir='z', offset=0, cmap='rainbow')
plt.show()
函数的凹凸性
凸函数的定义是:如果给定任意两个数x1,x2,如果满足以下式子就是凸函数

以y=x ** 2为例:
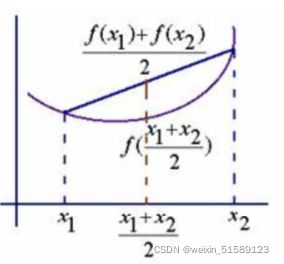
凸函数的最小值
通过y=x ** 2函数不难看出,最小值x = 0唯一存在,并且最小值点对应的函数切线与x轴平行,也就是在最小值点,函数的导数为0。这其实也凸函数求解最小值的一般方法:
a).对于一元函数,如果存在导数为0的点,则该点就是最小值点;
b).对于多元函数,如果存在某一点,使得函数的各个自变量的偏导数都为0,则该点就是最小值点。
因此,对于凸函数的最小值求解,最基本的出发点就是寻找导数为0的点。而最小二乘法也是基于偏导函数取值为0联立的方程组进行的求解。
SSE最小值
利用偏导等于0得出的方程组求解线性回归方程参数,就是最小二乘法求解过程。此处我们求得,对于(1, 2), (3, 4)这两个点来说,a=1,b=1时,SSE(a,b)取得最小值,也就是(1,1)是目标函数的最小值点。
4.机器学习建模一般流程
Step 1:提出基本模型
如本节中,我们试图利用一条直线(y=ax+b)去拟合二维平面空间中的点,这里我们所使用的这条直线,就是我们提出的基本模型。而在后续的深度学习的学习过程中,我们还将看到更为强大、同时也更加通用的神经网络模型。当然,不同的模型能够适用不同的场景,在提出模型时,我们往往会预设一些影响模型结构或者实际判别性能的参数,如简单线性回归中的a和b;
Step 2:确定损失函数和目标函数
接下来,围绕建模的目标,我们需要合理设置损失函数,并在此基础之上设置目标函数,当然,在很多情况下,这二者是相同的。例如,在上述简单线性回归中,我们的建模目标就是希望y=ax+b这条直线能够尽可能的拟合(1,2)、(3,4)这两个点,或者说尽可能“穿过”这两个点,因此我们设置了SSE作为损失函数,也就是预测值和真实值的差值平方和。当然,在计算过程中不难发现,SSE是一个包含了a和b这两个变量的方程,因此SSE本身也是一个函数(a和b的二元函数),并且在线性回归中,SSE既是损失函数(用于衡量真实值和预测值差值的函数),同时也是我们的目标函数(接下来需要优化、或者说要求最小值的函数)。这里尤其需要注意的是,损失函数不是模型,而是模型参数所组成的一个函数。
Step 3:根据目标函数特性,选择优化方法,求解目标函数
之前提到,目标函数既承载了我们优化的目标(让预测值和真实值尽可能接近),同时也是包含了模型参数的函数,因此完成建模需要确定参数、优化结果需要预测值尽可能接近真实值这两方面需求就统一到了求解目标函数最小值的过程中了,也就是说,当我们围绕目标函数求解最小值时,也就完成了模型参数的求解。当然,这个过程本质上就是一个数学的最优化过程,求解目标函数最小值本质上也就是一个最优化问题,而要解决这个问题,我们就需要灵活适用一些最优化方法。当然,在具体的最优化方法的选择上,函数本身的性质是重要影响因素,也就是说,不同类型、不同性质的函数会影响优化方法的选择。在简单线性回归中,由于目标函数是凸函数,我们根据凸函数性质,判断偏导函数取值为0的点就是最小值点,进而完成a、b的计算(也就是最小二乘法),其实就是通过函数本身的性质进行最优化方法的选取。
二、第一个优化算法:最小二乘法
1.最小二乘法的代数表示方法
2.手动代码验证最小二乘法
x = torch.tensor([[1., 1], [3, 1]])
y = torch.tensor([[2.], [4.]])
print(x)
'''
tensor([[1, 1],
[3, 1]])
'''
print(y)
'''
tensor([[2.],
[4.]])
'''
print(x.t())
'''
tensor([[1, 3],
[1, 1]])
'''
w = torch.mm(torch.mm(torch.inverse(torch.mm(x.t(), x)), x.t()), y)
print(w)
'''
tensor([[1.0000],
[1.0000]])
'''
和此前结果保持一致。当然,最小二乘法作为最优化问题的求解方法,我们可以这么理解w最终取值:当w取值为(1,1)时,自变量为w的SSE函数取得全域最小值。
3.lstsq实现最小二乘法
当然,我们也可以直接调用最小二乘法函数torch.lstsq(B, A)进行求解
print(torch.lstsq(y, x))
'''torch.return_types.lstsq(
solution=tensor([[1.0000],
[1.0000]]),
QR=tensor([[-3.1623, -1.2649],
[ 0.7208, -0.6325]]))
'''
对于lstsq函数来说,第一个参数是因变量张量,第二个参数是自变量张量,并且同时返回结果还包括QR矩阵分解的结果,QR分解也是一种矩阵分解方法,后续在涉及到QR分解内容时会详细进行讲解。
另外,在最小二乘法数学推导过程,涉及到矩阵范数的运算,在PyTorch中,我们使用linalg.norm函数求向量或矩阵的范数
t = torch.tensor([-1., 2])
#默认情况下,求解L2范数,各元素的平方和开平方
print(torch.linalg.norm(t))
#tensor(2.2361)
t = torch.tensor([-1., 2])
#默认情况下,求解L2范数,各元素的平方和开平方
print(torch.linalg.norm(t)) #norm默认计算的是二范式
#tensor(2.2361)
print(torch.sqrt(torch.tensor(5.)))
#tensor(2.2361)
#输入参数,求解l1范数,各元素的绝对值之和
print(torch.linalg.norm(t, 1))
#tensor(3.)
4.反向验证导数为零
a = torch.tensor(1., requires_grad=True)
print(a)
#tensor(1., requires_grad=True)
#此时a是一个可微分的张量,requires_grad是a的一个属性
#查看可微分性
print(a.requires_grad)
#True
#修改可微分性
a.requires_grad = False
print(a.requires_grad)
#False
a.requires_grad = True
b = torch.tensor(1., requires_grad=True)
print(b)
#tensor(1., requires_grad=True)
#然后创建损失函数
sse = torch.pow((2 - a - b), 2) + torch.pow((4-3 * a-b), 2)
print(torch.autograd.grad(sse, [a, b]))
#求sse在权重(1,1)上的偏导数
#(tensor(-0.), tensor(-0.))
至此,也可验证(1,1)是损失函数的最小值点。
torch.autograd.grad函数
x = torch.tensor(1., requires_grad=True)
print(x)
#tensor(1., requires_grad=True)
y = x ** 2
#导数计算记过
print(torch.autograd.grad(y, x))
#(tensor(2.),) 求y在x=1时的导数值