Zero-shot Learning零样本学习 论文阅读（一）——Learning to detect unseen object classes by between-class attribute

Learning to detect unseen object classes by between-class attribute这篇文章首次提出了Zero-shot Learning这一问题的概念，并给出了基于物体属性的解决方法。

算法概要

前提

$(x_1,l_1),\cdots ,(x_n,l_n)$为训练样本$x$和相应类别标签$l$，这样的成对数据共有$n$组，$l$中一共有$K$类，用$Y=\{y_1,\cdots ,y_K\}$表示， $Z=\{z_1,\cdots ,z_L\}$ 为测试集中所包含的$L$个类别，这里$Y$和$Z$就分别是可见类和不可见类，二者之间没有交集.

目标

学习一个分类器：$f:X\to Z$，也就是通过学习分类器，找到训练数据$x$和相应可见类别标签$l$与位置类别标签$Z$之间的关系。

思路

通过建立一个人工定义的属性层A，这个属性层是高维的、可以表征训练样本的各项特征，比如颜色、条纹等，目的是将基于图片的低维特征分类器转化到一个表征高维语义特征的属性层。这样可以使得分类器分类能力更广，具备突破类别边界的可能。
基于这个思路，作者提出了两种方法，分别是DAP和IAP.

具体原理

DAP(Directed attribute prediction)

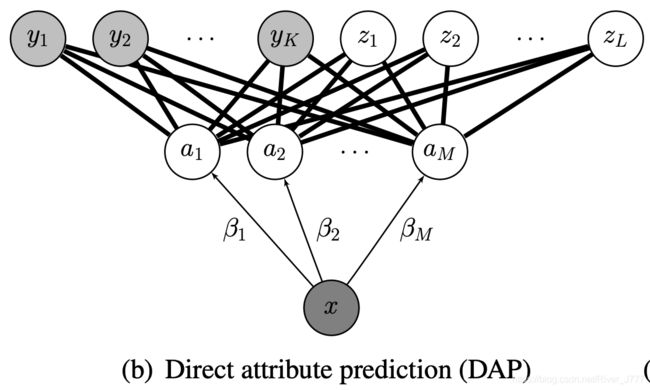
如下图，DAP在样本和训练类别标签之间加入了一个属性表示层A，$a$为$M$维属性向量$(a_1,\cdots ,a_M)$，每一维代表一个属性，且在$\{0,1\}$之间取值，对于每个标签都对应一个M维向量作为其属性向量（原型）。通过训练集$X$的对应属性进行训练，学习得到属性层的参数$\beta$，之后便可以得到$P(a|x)$，
将输入测试实例x输出的标签作为待估计的参数，对于测试实例x，即可利用MAP的思想，找出概率最大的类为输出的估计类。

MAP的原理见此链接https://blog.csdn.net/River_J777/article/details/111500068

z的后验概率为：
$$p(z\mid x)=\sum _{a\in \{0,1{\}}^M}p(z\mid a)p(a\mid x)$$
根据贝叶斯公式：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(a\mid z)p(z)}{p(a)}p(a\mid x)$$
根据文章中的假设前提各个维度属性条件独立（这个假设有点过强也是DAP主要问题所在）
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(a\mid z)p(z)}{p(a)}\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
根据Iverson bracket$[[x]]$，若其中语句为真则为1，否则为0，得 $p(a\mid z)=\left[\left[a=a^z\right]\right]$ ，可得：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(z)}{p(a)}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
由DAP的图模型知 $p\left(a^z\right)=p(a)$，可得：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(z)}{p\left(a^z\right)}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
整理得：
$$=\frac{p(z)}{p\left(a^z\right)}\sum _{a\in \{0,1{\}}^M}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
省略掉为零的项：
$$=\frac{p(z)}{p\left(a^z\right)}\prod _{m=1}^{M}p\left(a_m^z\mid x\right)$$
表示出z的后验概率后，对于输入测试实例x进入分类器后，分别测试不可见标签集$z_1,\cdots ,z_l$，求最大：
$$f(x)={\mathrm{argmax}}_{l=1,2,\dots \dots L\frac{p(z)}{p\left(a^{z_l}\right)}}\prod _{m=1}^{M}p\left(a_m^{z_l}\mid x\right)$$
根据属性之间独立：
$$={\mathrm{argmax}}_{l=1,2,\dots ..L}\frac{{\prod }_{m=1}^{M}p\left(a_m^{z_l}\mid x\right)}{{\prod }_{m=1}^{M}p\left(a_m^{z_l}\right)}$$
$$={\mathrm{argmax}}_{l=1,2,\dots ..L}\prod _{m=1}^M\frac{p\left(a_m^{z_l}\mid x\right)}{p\left(a_m^{z_l}\right)}$$
$f(x)$ 的输出即为对于输入x的预测标签.

IAP(Indirected attribute prediction)

区别于DAP，DAP的PGM中属性层是在实例层和标签层（包括可见和不可见）之间，而IAP则是将属性层置于可见标签层与不可见标签层之间，用来迁移可见类标签与实例的信息到不可见标签层。

原理和DAP类似，此时的后验概率为：
$$p\left(a_m\mid x\right)=\sum _{i=1}^{K}p\left(a_m\mid y_k\right)p\left(y_k\mid x\right)$$
得到这个后验后，再求出z的后验，即可如同DAP中一样应用MAP即可.