Zero-Shot Learning零样本学习 学习进展汇总

基本概念

最近刚入门学习零样本学习的相关内容，本次的笔记列出了一些零样本学习领域相关的概念，只有理解了这些概念才能更顺畅地阅读和理解文献。

什么是zero-shot learning?

一言以蔽之，zero-shot learning零样本学习就是让学习器对其从来没有见过的类别进行分类。比如：给学习器一堆马和老虎的图片进行训练，训练完毕后，我们输入一张斑马的照片，并希望学习器告诉我们“这是斑马！”。乍一听，这显然是不现实的。
但其实，我们输入的训练数据与希望识别的类别的并不会是完全无关的。显然，我们不会奢求学习器学习一些人脸、飞机等与斑马毫无关联的数据就可以在第一次看到斑马的图片的时候就能够识别出这是一匹斑马。另外，我们还会在零样本学习的过程中利用一些已有的知识，比如“斑马的外形像马，身上有条纹”。像这样，根据现有的马、老虎的照片以及“斑马的外形像马，身上有条纹”这条信息，我们尝试让学习器通过马的数据可以识别出马的外形，通过老虎的数据让学习器可以识别出动物身上的条纹，如果学习器发现一张输入的照片有马的外形+身上有条纹，那么学习器就有足够的信心认为这就是斑马，即使它之前从未见到过斑马的照片。怎么样，是不是刚才无厘头的ZSL任务，现在变得有了一些头绪～

基本概念

定义

上面用通俗易懂的语言介绍了ZSL，下面我们给出一些在正式学习之前需要了解的概念。

1. 特征空间(feature space)
   输入的具体的实例通常用特征向量表示，所有特征向量存在的空间就称为特征空间.
2. 可见类 & 不可见类(seen classes & unseen classes)
   在ZSL问题中，特征空间(feature space)包含一些带标签的训练实例，这些实例所涵盖的的类别就称为可见类(seen classes)；同时，特征空间中还包含一些不带标签的测试实例，这些实例所属的类别称为不可见类(unseen classes).
   接着我们就可以给出ZSL的具体定义：
3. Zero-Shot Learning
   对于给定属于可见类集合$S$的测试实例$D^{tr}$以及属于不可见类集合$U$的测试实例$X^{te}$， Zero-Shot Learning目标是学习一个分类器$f^u(\cdot ):X\to U$，使得可以预测不可见类的测试实例的类别.

语义空间(Semantic Spaces)

Zero-Shot Learning中不可或缺的一部分就是有关类的语义信息，比如上文提到的“不可见类斑马的外形像马，身上有条纹”，这些有关类的语音信息构成了语义空间.我们可以将 Zero-Shot Learning中用到的语义空间根据构造方法分为工程语义空间和学习语义空间。

工程语义空间(Engineered Semantic Spaces)

在工程语义空间中，每个维度的信息都是由人工设计的，接下来是几个 Zero-Shot Learning经常用到的工程语义空间。

1. 属性空间(Attribute spaces)
   属性空间是由一组属性构成的语义空间。在属性空间中，描述类的各种属性的术语列表被定义为属性。每个属性通常是短语或词语，如在动物识别的任务中，身体颜色(“黄色”“白色”等等)、栖息地(“陆地”“海洋”“沙漠”等等)都是属性，属性的集合就构成了属性空间。
   我们还能在论文中看到的一个词prototype，翻译过来是原型，对于每个类，对应原型的每个维度的值由该类是否具有对应的属性决定。比如，若我们构建的属性空间中包含三个属性，“有条纹”“生活在陆地”和“食草的”，那么对于“老虎”这一类三个属性的对应值分别为1、1、0，那么就可以构成原型[1,1,0].
2. 词汇空间(Lexical Space)
   词汇空间是由一组词汇项构造的各种语义空间。 词汇空间基于可以提供语义信息的类和数据集的标签。 数据集可以是一些结构化的词汇数据库，例如WordNet.
3. 文本关键字空间(Text-keyword Spaces）
   文本关键字空间是一种由从每个类的文本描述中提取的一组关键字构成。 在文本关键字空间中，文本描述的最常见来源是网站，包括维基百科等一般网站和特定于域的网站。 例如，任务是图像中的zero-shot flower识别，因此使用植物数据库和植物百科全书（其特定于植物）来获得每个花类的文本描述。 除了预定义的网站之外，还可以从搜索引擎获得这样的文本描述。
   此外，还有一些基于特定问题的空间(Some problem-specific spaces)。

基于以上工程语义空间的概念，我们可以发现工程语义空间的优点是通过语义空间和类原型的构建，灵活的编码人类领域知识；缺点是严重依赖人来执行语义空间和类原型工程。例如，在属性空间中，属性设计需要手工完成，这需要领域专家付出巨大努力。

学习语义空间(Learned Semantic Spaces)

在学习语义空间中，每个类的原型都是通过学习输出中获得。但是，在这些原型中，每个维度都没有明确的语义，而是语义信息包含在了整个原型中。用于提取原型的模型可以进行预先训练。

1. 标签嵌入空间(Label-embedding Spaces)
   标签嵌入空间是一类通过嵌入类标签来获得类原型的语义空间。可以利用在NLP领域已经得到了广泛的发展和应用的单词嵌入技术。单词嵌入技术中，单词和短语作为向量被嵌入到实数空间中。
   有关词嵌入技术，可以看一下这个链接的介绍.
   https://www.pianshen.com/article/4510216822/
2. 文本嵌入空间(Text-embedding spaces)
   文本嵌入空间通过嵌入每个类的文本描述来获得类原型的语义空间。与文本关键字空间类似，文本嵌入空间中的语义信息也来自文本描述。不同的是，文本嵌入空间是通过一些学习模型将每个类的文本描述用作模型的输入，输出向量被视为该类的原型。
3. 图像表示空间(Image-representation spaces)
   图像表示空间是通过每个类的图像来获得类原型的语义空间。

学习语义空间的优势在于需要较少的人工介入，可以照顾到一些很可能被人类忽略的语音信息；不足之处也很明显，语义空间每个维度的语义都是隐式的。

本篇文章部分内容来自于2019年的一篇综述A Survey of Zero-Shot Learning: Settings, Methods, andApplications.

最大后验概率

最大后验估计MAP是最常用的几个参数点估计之一，基本原理由贝叶斯定理而来，先看贝叶斯公式：
$$P\left(\theta \mid \mathbf{x}\right)=\frac{P\left(\mathbf{x}\mid \theta \right)P\left(\theta \right)}{P(\mathbf{x})}$$
其中，我们将$P\left(\theta \right)$称为先验概率，即在事情发生之前，根据以往的经验等推测未来此事件发生的概率；将$P\left(\theta \right|\mathbf{x})$称为后验概率，即在事情发生之后，分析由各种原因导致发生的概率。
$P\left(\mathbf{x}\mid \theta \right)$就是极大似然估计MLE的式子。
贝叶斯分类器就是根据先验概率利用贝叶斯公式计算出各种分类的后验概率，选择最大的后验概率所对应的分类结果。
贝叶斯公式可以形象的写成：
$$\text{后验概率}=\frac{\text{似然函数}\cdot \text{先验概率}}{\text{数据分布}}$$
最大后验估计MAP就是将后验概率取得最大值时待估参数$\theta$的值$\hat{\theta }$作为参数的点估计。
这里$P(X)$与参数$\theta$没有关系，因此我们只要求分子最大即可，即
$$\begin{array}{rl}{\hat{\theta }}_{MAP}& ={\mathrm{argmax}}_{\theta }\frac{p(X\mid \theta )p(\theta )}{p(X)}\\ & ={\mathrm{argmax}}_{\theta }p(X\mid \theta )p(\theta )\\ & ={\mathrm{argmax}}_{\theta }\{L(\theta \mid X)+\log p(\theta )\}\\ & ={\mathrm{argmax}}_{\theta }\left\{\sum _{x\in X}\log p(x\mid \theta )+\log p(\theta )\right\}\end{array}$$

论文阅读（一）DAP&IAP

Learning to detect unseen object classes by between-class attribute这篇文章首次提出了Zero-shot Learning这一问题的概念，并给出了基于物体属性的解决方法。

算法概要

前提

$(x_1,l_1),\cdots ,(x_n,l_n)$为训练样本$x$和相应类别标签$l$，这样的成对数据共有$n$组，$l$中一共有$K$类，用$Y=\{y_1,\cdots ,y_K\}$表示， $Z=\{z_1,\cdots ,z_L\}$ 为测试集中所包含的$L$个类别，这里$Y$和$Z$就分别是可见类和不可见类，二者之间没有交集.

目标

学习一个分类器：$f:X\to Z$，也就是通过学习分类器，找到训练数据$x$和相应可见类别标签$l$与位置类别标签$Z$之间的关系。

思路

通过建立一个人工定义的属性层A，这个属性层是高维的、可以表征训练样本的各项特征，比如颜色、条纹等，目的是将基于图片的低维特征分类器转化到一个表征高维语义特征的属性层。这样可以使得分类器分类能力更广，具备突破类别边界的可能。
基于这个思路，作者提出了两种方法，分别是DAP和IAP.

具体原理

DAP(Directed attribute prediction)

如下图，DAP在样本和训练类别标签之间加入了一个属性表示层A，$a$为$M$维属性向量$(a_1,\cdots ,a_M)$，每一维代表一个属性，且在$\{0,1\}$之间取值，对于每个标签都对应一个M维向量作为其属性向量（原型）。通过训练集$X$的对应属性进行训练，学习得到属性层的参数$\beta$，之后便可以得到$P(a|x)$，
将输入测试实例x输出的标签作为待估计的参数，对于测试实例x，即可利用MAP的思想，找出概率最大的类为输出的估计类。

MAP的原理见此链接https://blog.csdn.net/River_J777/article/details/111500068

z的后验概率为：
$$p(z\mid x)=\sum _{a\in \{0,1{\}}^M}p(z\mid a)p(a\mid x)$$
根据贝叶斯公式：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(a\mid z)p(z)}{p(a)}p(a\mid x)$$
根据文章中的假设前提各个维度属性条件独立（这个假设有点过强也是DAP主要问题所在）
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(a\mid z)p(z)}{p(a)}\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
根据Iverson bracket$[[x]]$，若其中语句为真则为1，否则为0，得 $p(a\mid z)=\left[\left[a=a^z\right]\right]$ ，可得：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(z)}{p(a)}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
由DAP的图模型知 $p\left(a^z\right)=p(a)$，可得：
$$=\sum _{a\in \{0,1{\}}^M}\frac{p(z)}{p\left(a^z\right)}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
整理得：
$$=\frac{p(z)}{p\left(a^z\right)}\sum _{a\in \{0,1{\}}^M}\left[\left[a=a^z\right]\right]\prod _{m=1}^{M}p\left(a_m\mid x\right)$$
省略掉为零的项：
$$=\frac{p(z)}{p\left(a^z\right)}\prod _{m=1}^{M}p\left(a_m^z\mid x\right)$$
表示出z的后验概率后，对于输入测试实例x进入分类器后，分别测试不可见标签集$z_1,\cdots ,z_l$，求最大：
$$f(x)={\mathrm{argmax}}_{l=1,2,\dots \dots L\frac{p(z)}{p\left(a^{z_l}\right)}}\prod _{m=1}^{M}p\left(a_m^{z_l}\mid x\right)$$
根据属性之间独立：
$$={\mathrm{argmax}}_{l=1,2,\dots ..L}\frac{{\prod }_{m=1}^{M}p\left(a_m^{z_l}\mid x\right)}{{\prod }_{m=1}^{M}p\left(a_m^{z_l}\right)}$$
$$={\mathrm{argmax}}_{l=1,2,\dots ..L}\prod _{m=1}^M\frac{p\left(a_m^{z_l}\mid x\right)}{p\left(a_m^{z_l}\right)}$$
$f(x)$ 的输出即为对于输入x的预测标签.

IAP(Indirected attribute prediction)

区别于DAP，DAP的PGM中属性层是在实例层和标签层（包括可见和不可见）之间，而IAP则是将属性层置于可见标签层与不可见标签层之间，用来迁移可见类标签与实例的信息到不可见标签层。

原理和DAP类似，此时的后验概率为：
$$p\left(a_m\mid x\right)=\sum _{i=1}^{K}p\left(a_m\mid y_k\right)p\left(y_k\mid x\right)$$
得到这个后验后，再求出z的后验，即可如同DAP中一样应用MAP即可.

论文阅读（二）EsZSL

这篇论文提出了一种新的zero-shot learning方法“Embarrassingly simple Zero-Shot Learning”，后来被简写作EsZSL。之所以叫做“embarrassingly simple”，是因为这种新方法只需要一行代码就可以实现，而且在zero-shot learning的几个标准数据集上的表现要优于当时最先进的方法。

ESZSL算法概况

背景

在本篇论文之前zero-shot learning相关的文章更多关注点是attribute learning，从训练实例中提取标签属性，直至《Learning To Detect Unseen Object Classes by Between-Class Attribute Transfer》首次定义了Zero-shot learning并且提出了DAP、IAP，尽管DAP这种方法在一些方面得到应用和进一步研究，但是其弊端也比较明显，主要体现在两方面，一方面是他无法对输出的预测给出可靠性度量，二是算法做出了一些过强的假设，尤其是“各属性之间条件独立”，比如“是否生活在陆地”“是否生活在农场”这两个属性显然不是互相独立的。

前提

假设一共有z个类，其中每个类对应于属性空间中的a维属性向量，称为某个类的signature；集合的所有类用矩阵表示就是属性空间$S\in [0,1{]}^{a\times z}$；有m个实例，维度为d维，写成矩阵形式$X\in R^{d\times m}$，实例的标签$Y=\{-1,1{\}}^{m\times z}$.

思路

在实例空间X和和标签空间Y中间添加一个属性空间，并且通过一个新的映射$V$连接属性空间和特征空间，最后建立损失函数.

算法原理

模型

从一个一般的线性分类器的原理开始，以岭回归为例，其优化过程就是：
$$mi{n}_{w}L(X^{T}W,Y)+\Omega (W)$$
其中$L$为损失函数，$\Omega$为正则化项.
为了实现zero-shot learning，中间添加一个属性空间$S$，通过映射$V$连接属性空间$S$和特征空间$X$，即
$$W=VSV\in R^{d\times a}$$
那么上式就变为
$$\underset{V}{\min }L\left(X^{\top }VS,Y\right)+\Omega (V)$$
通过学习得到参数$V$后，输入新的$x$和$S^{\ast }$，就可以根据$argma{x}_i{x}^{T}V{S}_{\cdot ,i}^{\ast }$确定预测的类别。

求解

上面得到的式子
$$\underset{V}{\min }L\left(X^{\top }VS,Y\right)+\Omega (V)$$
由两部分组成，一部分是损失函数$L$，另一部分是正则化$\Omega$.

损失函数$L$

损失函数$L$论文中直接定义为Frobenius范数的形式：$$L(P,Y)=\Vert P-Y{\Vert }_{Fro}^2$$

正则化项$\Omega$

对于正则化项的选择，作者有两点考虑：

1. 应该包含对于$VS$的约束，是因为$VS$代表属性空间中的向量在特征空间中的投影，对$VS$加以约束，理想上保证了所有signature在特征空间里在空间离有相似的欧几里得范数，能够更公平的比较不同的signature，同时能够防止由于高度不平衡数据引发的问题。
2. 还应该包含对$V^{T}X$的约束，是因为 $V^{T}X$是所有训练实例$X$在属性空间中的表征，对于$V^{T}X$进行约束，可以限制其方差，使其在训练特征分布中拥有足够的不变性，如同传统的ridge和lasso一样，提高模型在不同的测试特征分布中的泛化性。

以此，可以设定：
$$\Omega (V)=\gamma \Vert VS{\Vert }_{Fro}^2+\lambda {\Vert X^{\top }V\Vert }_{Fro}^2+\beta \Vert V{\Vert }_{Fro}^2$$
其中 $\gamma ,\lambda ,\beta$ 为超参数，此处不妨设 $\beta =\lambda \gamma$ ，后面会用到.

综合损失函数和正则化项，目标函数现在可以具体得到：
$$min{\Vert X^{\top }VS-Y\Vert }_{Fro}^2+\gamma \Vert VS{\Vert }_{Fro}^2+\lambda {\Vert X^{\top }V\Vert }_{Fro}^2+\beta \Vert V{\Vert }_{Fro}^2$$
显然这是一个凸函数，因此我们可以直接对需要优化的参数$V$求导，令导函数为零，求解V即可。
将$$min\{{\Vert X^{\top }VS-Y\Vert }_{Fro}^2\}+\{\gamma \Vert VS{\Vert }_{Fro}^2+\lambda {\Vert X^{\top }V\Vert }_{Fro}^2+\beta \Vert V{\Vert }_{Fro}^2\}$$
写作两部分$minA+B$
$$\frac{\partial A}{\partial V}=\frac{\partial {\Vert X^{\top }VS-Y\Vert }_{Fro}^2}{\partial V}$$
由Frobenius范数定义$\Vert X{\Vert }_{Fro}^2=\mathrm{tr}\left(X^{\top }X\right)$，得到

$$=\frac{\partial tr\left({\left(X^{\top }VS-Y\right)}^{\top }\left(X^{\top }VS-Y\right)\right)}{\partial V}$$
计算矩阵的转置并展开括号：
$$=\frac{\partial \mathrm{tr}\left(S^{\top }{V}^{\top }X{X}^{\top }VS+Y^{\top }Y-S^{\top }{V}^{\top }XY-Y^{\top }{X}^{\top }VS\right)}{\partial V}$$
根据迹的性质$tr(A+B)=tr(A)+tr(B)tr(AB)=tr(BA)$:
$$=\frac{\partial \mathrm{tr}\left(S^{\top }{V}^{\top }X{X}^{\top }VS+Y^{\top }Y-2Y^{\top }{X}^{\top }VS\right)}{\partial V}$$
省略与$V$无关的项：
$$=\frac{\partial \mathrm{tr}\left(S^{\top }{V}^{\top }X{X}^{\top }VS-2Y^{\top }{X}^{\top }VS\right)}{\partial V}($$
根据迹的性质$tr(AB)=tr(BA)$:
$$=\frac{\partial \mathrm{tr}\left(VS{S}^{\top }{V}^{\top }X{X}^{\top }-2VS{Y}^{\top }{X}^{\top }\right)}{\partial V}$$
根据：$\frac{\partial \mathrm{tr}(AB)}{\partial A}=B^T$，$\frac{\partial \mathrm{tr}\left(AB{A}^{T}C\right)}{\partial A}=CAB+C^{T}A{B}^T$

（证明：
$$\frac{\partial \mathrm{tr}(AB)}{\partial A}=\frac{\partial {\sum }_{i=1}^m{\sum }_{j=1}^n{a}_{ij}{b}_{ji}}{\partial {\sum }_{i=1}^m{\sum }_{j=1}^n{a}_{ij}}=\sum _{i=1}^m\sum _{j=1}^n{b}_{ji}=B^T$$

$$\frac{\partial tr\left(AB{A}^{T}C\right)}{\partial A}=\frac{\partial tr\left(A^{T}CAB\right)}{\partial A}\begin{array}{l}={\left(B{A}^{T}C\right)}^T+CAB=C^{T}A{B}^T+CAB\end{array})$$
最终得到
$$=2X{X}^{\top }VS{S}^{\top }-2XY{S}^{\top }$$

参考文献

[1]Romera-Paredes B , Torr P H S . An embarrassingly simple approach to zero-shot learning[C]// Proceedings of the 32nd international conference on Machine learning (ICML '15). JMLR.org, 2015.

论文阅读（三）SAE

Semantic Autoencoder for Zero-Shot Learning提出的算法被简称为SAE，首次引入了自编码器结构，一定程度上解决了zero-shot learning中主要问题之一的领域漂移(domain shift)问题，直接导致之后的新方法大都采用了这种自编码器的结构。

背景

领域漂移(domain shift)

领域漂移问题首次被提出是在《Transductive Multi-View Zero-Shot Learning》这篇文章中，简单来说就是同一属性在不同的类别中，视觉特征的差异可能很大。比如，斑马和猪都有尾巴，那么在类别语义表示中，对于“有尾巴”这一属性，斑马和猪都是值“1”，但是在图片数据中，两者尾巴的视觉特征却差异很大，如果用猪的图片来训练，需要预测的是斑马，就很难达到预期的目标。

自编码器

自编码器（Autoencoder）是一种利用反向传播算法使得输出值等于输入值的神经网络，它先将输入压缩成潜在空间表征，然后通过这种表征来重构输出。
例如，我们输入一张图片，通过encoder将其现压缩成潜在表征(Latent Representation)，再通过decoder将潜在表征重构成图片作为输出。

因此，自编码器由两部分组成：

1. 编码器，将输入压缩成潜在空间表征，用函数$h=f(x)$表示；
2. 解码器，重构潜在空间表征得到输出，用函数$s=g(h)$表示。

自编码器就可以用函数$g(f(x))=s$表示，$x$是输入，$s$是输出，让$x$和$s$相近。
那么，让输出和输入的东西一样，那这个自编码器还有什么用呢？
其实，我们的目的在于，通过训练输出值等于输入值的自编码器，让潜在表征$h$作为有价值的属性。
通常，为了从自编码器获得有用特征，我们会限制h的维度使其小于输入x，使得自编码器能学习到数据中最重要的特征。

算法原理

思路

在传统的自编码器的目标函数$mi{n}_{W,W^{\ast }}\Vert X-W^{\ast }WX{\Vert }_F^2$中，为了使中间层能够表征属性，在这个目标函数中加入一个约束$WX=S$，$S$为属性对应的语义向量，即$mi{n}_{W,W^{\ast }}\Vert X-W^{\ast }WX{\Vert }_F^2,s.t.WX=S$，以此来最优化求解。

设定

$X\in R^{d\ast N}$ 代表 $d$ 维共 $N$ 个特征向量组成的矩阵，投影矩阵 $W\in R^{k\ast d},$ 将特征向量投影到语义空间, 得到latent representation $S\in R^{k\ast N},$ 假设 $k<d$，通过一个投影矩阵 $W^{\ast }\in R^{k\ast d},$ 将语义向量投影到特征空间。 $Y=\left\{y_1,y_2,\dots \dots y_s\right\}$ 为s个可见类标签的标签向量, $Z=\left\{z_1,z_2,\dots \dots ,z_u\right\}$ 为u个不可见类标签的标签向量, $Y\cap Z=\varphi$ 。 $S_Y=\left\{s_1,s_2,\dots .s_s\right\}$ 为可见类标签的prototype的集合, $S_Z=\left\{s_1,s_2,\dots ..s_u\right\}$ 为不可
见类标签的prototype的集合, $X_Y=\left\{\left(x_i,y_i,s_i\right)\right\}\in R^{d\ast N}$ 为拥有N个k维训练样本 $x_i$ 的训练 集,测试集 $X_Z=\left\{\left(x_i,y_i,s_i\right)\right\}$ 其中 $y_i,s_i$ 未知.

算法原理

上图表示了本文中的自编码器结构，以传统的自编码器的思想，本问题的目标函数为$$mi{n}_{W,W^{\ast }}\Vert X-W^{\ast }WX{\Vert }_F^2$$
为了使中间层能够表征属性，在这个目标函数中加入一个约束$WX=S$，$S$是实现定义好的属性对应的语义向量，目标函数为：$$mi{n}_{W,W^{\ast }}\Vert X-W^{\ast }WX{\Vert }_F^2,s.t.WX=S$$
考虑到zero-shot learning旨在提高大规模计算机视觉的速度，为了减少参数数量，设置$W^{\ast }=W^T$，则目标函数可以化为 ：
$$mi{n}_W\Vert X-W^{T}S{\Vert }_{Fro}^2,s.t.WX=S$$
显然，约束$WX=S$有点过于强了，所以将其变为一个软约束加入目标函数：
$$mi{n}_W\Vert X-W^{T}S{\Vert }_{Fro}^2+\lambda \Vert WX=S{\Vert }_{Fro}^2$$
其中，$\lambda$为超参数
显然这是一个凸优化问题，通过对$W$求导，令导数为零，求解$W$即可。
$\frac{\partial \left({\Vert X-W^{\top }S\Vert }_{Fro}^2+\lambda \Vert WX-S{\Vert }_{Fro}^2\right)}{\partial W}$
$=\frac{\partial \left(tr\left({\left(X^{\top }-S^{\top }W\right)}^{\top }\left(X^{\top }-S^{\top }W\right)+\lambda (WX-S{)}^{\top }(WX-S)\right)\right)}{\partial W}$
$=\frac{\partial (tr\left(W^{\top }S{S}^{\top }W-2W^{\top }S{X}^{\top }+\lambda \left(X^{\top }{W}^{\top }WX-2S^{\top }WX\right)\right)}{\partial W}$
$=\frac{\partial tr\left(W^{\top }S{S}^{\top }W\right)}{\partial W}-2\frac{\partial tr\left(W^{\top }S{X}^{\top }\right)}{\partial W}+\lambda \frac{\partial tr\left(X^{\top }{W}^{\top }WX\right)}{\partial W}-2\lambda \frac{\partial tr\left(S^{\top }WX\right)}{\partial W}$
$=\frac{\partial tr\left(X^{\top }SW\right)}{\partial W}+\lambda \frac{\partial tr\left(WX{X}^{\top }{W}^{\top }\right)}{\partial W}-2\lambda \frac{\partial tr\left(X{S}^{\top }W\right)}{\partial W}$
$=2S{S}^{\top }W-2S{X}^{\top }+2\lambda WX{X}^{\top }-2\lambda S{X}^{\top }$
$=0$
令 $A=S{S}^{\top },B=\lambda X{X}^{\top },C=(1+\lambda )S{X}^{\top }$
则等式可以写作：
$AW+WB=C$
此为著名的Sylvester方程的标准形式，可利用Bartels-Stewart algorithm求解，值得注意的是，Bartels-Stewart algorithm算法的复杂度为$o(d^3)$ ,与训练集大小无关，因此在大规模数据集上同样可以表现优异。

具体流程

对于测试特征向量$x_i$，有两种方式给出预测，其中距离度量记作$D(x,y)$

1. $S_{Z_j}$ 为未见类标签集中第 $j$ 个类在属性空间中对应的属性向量，也就是原型prototype
   $\Phi \left(x_i\right)={\mathrm{argmin}}_{j}D\left(W{x}_i,S_{Z_j}\right)$
2. $s_i$ 为不可见标签集中的一个元素
   $\Phi \left(x_i\right)={\mathrm{argmin}}_{j}D\left(x_i,W{s}_j\right)$
   $\Phi \left(x_i\right)$ 的值为输出的预测值。

实验结果表明两种形式输出非常相似。

参考文献

[1]Kodirov E , Xiang T , Gong S . Semantic Autoencoder for Zero-Shot Learning[J]. 2017.

论文阅读（四）DMaP

这篇2017年的论文提供了解决semantic gap问题的简单做法，所谓的semantic gap也就是从图片中提取的低层特征到高层语义之间存在的“语义鸿沟”问题。这与上一篇论文提到的领域漂移问题都是zero-shot learning技术瓶颈问题之一。

背景

流形学习

首先，什么是流形？
流形(manifold)是局部具有欧式空间性质的空间，包括各种纬度的曲线曲面，例如球体、弯曲的平面等。流形的局部和欧式空间是同构的。
流形学习（manifold learning）是机器学习、模式识别中的一种方法，在维数约简方面具有广泛的应用。它的主要思想是将高维的数据映射到低维，使该低维的数据能够反映原高维数据的某些本质结构特征。流形学习的前提是有一种假设，即某些高维数据，实际是一种低维的流形结构嵌入在高维空间中。流形学习的目的是将其映射回低维空间中，揭示其本质。

语义间隔

样本的特征往往是视觉特征，比如用深度网络提取到的特征，而语义表示却是非视觉的，这直接反应到数据上其实就是：样本在特征空间中所构成的流型与语义空间中类别构成的流型是不一致的。而语义间隔问题就是样本在特征空间中的流形与语义空间中的类别构成的流形是有差异的。解决此问题的思路便是将二者的流型调整至一致。

算法原理

算法思路

要解决的问题是将特征空间中的流形与语义空间中的类别构成的流形，最简单的思路便是将类别的语义表示调整到样本的流形，即用类别语义表示的K近邻样本点重新表示类别语义。

符号设定

1. 可见（训练）标签集 $L_s=\left\{l_s^1,l_s^2\dots \dots l_s^m\right\}$ (共有 $m$ 个类) ，其在语义空间中对应的prototype集为 $K_s=\left\{k_s^1,k_s^2\dots \dots k_s^m\right\}$；
2. 不可见 (测试) 标签集 $L_u=\left\{l_u^1,l_u^2\dots \dots l_u^l\right\}$
   (共 $l$ 个类) ，其在语义空间中对应的prototype集为 $$K_u=\left\{k_u^1,k_u^2\dots \dots k_u^l\right\}$;
3. 特征表征集 $X_s=\left\{x_1,x_2,\dots \dots ,x_n\right\}$,其中 $x_i$ 对应第 $i$ 个图像的提取特征；
4. 训练集 $D_s={\left\{\left(x_i,y_i,k_i\right)\right\}}_{i=1}^n,x_i\in X_s$, $y_i\in L_s$.

算法流程

训练：

1. 使用传统的方法求解特征空间到属性空间的映射 $f_s$,即求解投影矩阵 $W$
   $W={\mathrm{argmin}}_{W}l\left(WX,K_s\right)+\Omega (W)$
   其中 $l(X,Y)$ 为损失函数, $\Omega (W)$ 为正则化项
2. 对于所有的 $k_s^i$,对所有的训练样本在语义空间的投影 ${\left\{f_s\left(x_i\right)\right\}}_{i=1}^n$
   求m（m为超参数) 个最近邻，并赋值: ${\tilde{k}}_s^i=\frac{1}{m}{\sum }_{m\text{个}{k}_s^i\text{ 的最近邻 }}{f}_s\left(x_i\right)$
   并用 ${\tilde{k}}_s^i$ 构建新的语义空间 $\tilde{s}$
3. 反复迭代1，2直至收敛.

测试：
对于测试特征矩阵 $X_u,$ 如同step2，对于所有的 $k_u^i$ 求m个最近邻并赋值构建新的语 义空间，并一样进行迭代，最后得到最终的映射 ${\tilde{f}}_s,\tilde{u},$ 再通过余弦距离输出预测：
$j={\mathrm{argmin}}_{j}d\left(f_s\left(x_j\right),k_c\right)$

论文阅读（五）DeViSE

这篇2013年的文章提出了DeViSE这种方法，主要是综合了传统视觉识别的神经网络和词向量处理(word2vec)中的skip-gram模型，实现了一个视觉和语义兼顾的ZSL模型，取得了较好的效果，时至今日准确率仍然可以排在前面。

背景

Skip-gram

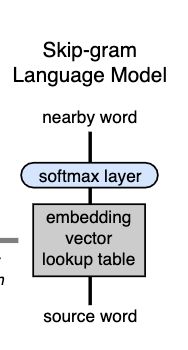
Skip-gram是Word2Vec模型中的一种，给定一个input word来预测上下文，训练之后的模型的目的并不是用这个模型来预测，而是为了得到这模型隐层中学得的权重参数。
首先，我们构建一个完整的神经网络，包含输入层、隐层、输出层。
例如，对于一个句子“I want to eat an apple.” 选取一个词作为输入，这里选择"eat"，再定义一个参数skip-window,它代表着我们从当前input word的一侧（左边或右边）选取词的数量。如果我们设置$skip\_window=2$，就代表选取输入词左边2个和右边2个单词进入窗口[“want”,“to”,“an”,“apple”]；另外一个参数num-skips，代表我们从窗口中选取多少个不同的词，作为我们的output，当$skip\_window=1，skip\_num=2$时，我们将会得到两组 (input word, output word) 形式的训练数据，即 (“eat”, “to”)，(“eat”, “I”).
神经网络基于这些训练数据将会输出一个概率分布，这个概率代表着我们词典中的每个词是output word的可能性。例如，上面我们得到两组数据。我们先用一组数据('来训练神经网络，那么模型通过前面学习这个训练样本，会告诉我们词汇表中其他单词的概率大小和“eat”的概率大小。
具体地，因为神经网络的的输入必须为数值，所以我们会首先将词汇表中的单词进行one-hot编码，隐层不使用任何激活函数，但是输出层用softmax.

算法

算法思路

分别预训练一个视觉网络和一个词向量skip-gram网络，再结合两个网络进行训练。

原理

预训练一个视觉模型如下图：

和一个skip-gram模型，如下：

将两个模型整合：

具体：

1. 语义模型
   通过Skip-gram对模型进行训练，Skip-gram为通过单词来预测单词的上下文，训练模型最后得到一个权重矩阵，该矩阵即为需要的Embedding矩阵。
2. 视觉模型
   采用了1,000-class ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2012 这篇文章提出的模型，并将结果作为benchmark。
3. Deep Visual Semantic Embedding Model
   即本文提出的模型。输出层去掉了之前的softmax，换成了一个将4096维向量（图像）映射到500或1000维（词向量）的线性映射transformation。
4. 损失函数：使用点积相似性（dot-product similarity）和铰链损失函数（hinge rank loss）结合来作为该模型的损失函数，这可以使得在图像模型的输出和该图像对应的正确的标签的向量表示之间的点积相似性，要比不正确的其他标签的向量与该图像的相似性高。
   定义：对于输入的image, core visual model的输出为 $\bar{v}($image$)$ ,transformation模块的线性映射参数为 $M$,标签label，经过skip-gram模型的输出为 ${\bar{t}}_{\text{label}}$ 其中 image对应label，相似性度量为点积度量，同时结合了hinge rank loss，而未采用 $l_2$ loss论文的 解释为分类问题(最近邻问题)本质为排名问题，即正确的标签排名应高于错误的标签,而 $l_2$ loss仅 仅是考虑了让预测向量与正确的向量尽可能接近，却忽略了预测向量与其它错误向量的距离，实验 结果也证明 $l_2$ loss效果不如hinge rank loss, 因此loss为：
   $$l(\text{image,label})=\sum _{j\ne label}\max \left[0,\mathrm{margin}-\left({\bar{t}}_{\text{label}}M\bar{v}(\text{image})-{\bar{t}}_{j}M\bar{v}(\text{image})\right)\right]$$
   其中margin为超参数，实验中设置为0.1

参考文献

[1]A. Frome et al., ‘DeViSE: A Deep Visual-Semantic Embedding Model’, p. 9.

论文阅读（六）f-CLSWGAN

这篇CVPR 2018年发表的论文提出用对抗生成网络GAN来在特征空间生成数据的思想来解决zero-shot learning的问题。

背景

生成对抗网络GAN

生成对抗网络GAN是源自博弈论中的零和博弈，由两部分组成，分别是生成模型G(generative model)和判别模型(discriminative model)。
整个模型的目的是输入原始数据x和随机噪声信号z ，然后判别输出这个输入是真实数据还是生成的样本。

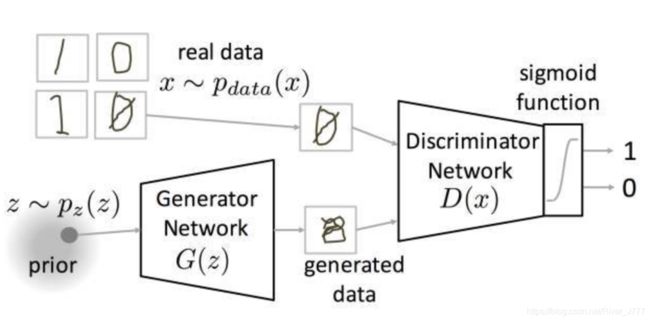
$X$是真实数据，真实数据符合$P_{data}(x)$分布。$z$是噪声数据，噪声数据符合$P_z(z)$分布，比如高斯分布或者均匀分布。然后从噪声$z$进行抽样，通过$G$之后生成数据$x=G(z)$。然后把生成数据们和原始数据们都送入分类器$D$，后面接一个sigmoid函数，输出判定类别。

对于生成器来说，其要尽可能产生与原始数据相近分布的数据，也就是生成数据的分布与原始分布差距尽可能小；对于判别器来说，要尽可能判别出输入数据是属于原始数据还是属于生成数据；
我们给出优化函数：
$$\underset{G}{\min }\underset{D}{\max }V(D,G)$$
$$V(D,G)={\mathbb{E}}_{x\sim p_{\text{data }}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z))]$$
具体优化过程略。
根据其原理，不难理解GAN的用途：产生数据、模拟分布代替原始数据。

算法模型

思路

作者使用GAN在特征空间生成数据，因为可以将zero-shot learning问题看作是数据缺失的问题，所以我们可以考虑生成目标域的数据，而生成特征数据比生成图像数据能取得更好的结果。

模型

本文的基本模型如图所示：

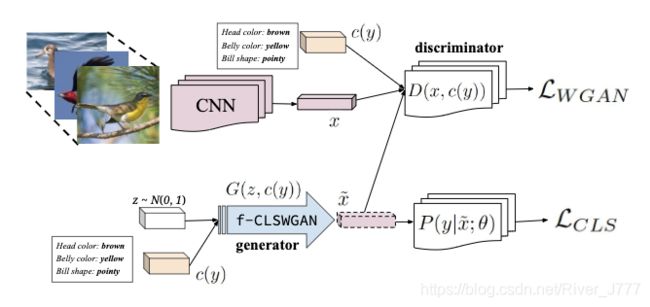
上面的一部分是通过CNN提取真实图像数据的特征，里面的CNN可以用GoogleNet或ResNet，可以是从ImageNet上预训练的模型，也可以是在特定任务中微调过的模型，本文中采用的是预训练模型；首先利用CNN网络提取特征$x$；然后将特征$x$与其对应的属性描述$c(y)$ 拼接后输入判别器，并判别为真。
下面一部分是生成数据的分支随机生成一个变量，与属性描述拼接后输入生成器，生成特征大，再次将 $\hat{x}$ 与属性描述 $c(y)$ 拼接后输入判别器并判别为假。
为提高生成质量，加一个auxiliary classifier, 对生成的数据进行分类，类别为 $y_{\circ }$。
优化的过程跟传统GAN类似。

参考文献

[1]Y. Xian, T. Lorenz, B. Schiele, and Z. Akata, ‘Feature Generating Networks for Zero-Shot Learning’, ArXiv171200981 Cs, Apr. 2018, Accessed: Jan. 12, 2021. [Online]. Available: http://arxiv.org/abs/1712.00981.

论文阅读（七）Unsupervised Domain Adaptation

这篇论文运用了一个unsupervised domain adaptation的技巧结合正则化字典稀疏学习，主要解决zero-shot learning中的domain shift问题。

背景

字典稀疏学习

1. 稀疏表示
   假如我们用矩阵$X=\{x_1,x_2,\cdots ,x_n\}\in R^{d\times n}$表示数据集，每一列代表一个样本，即$n$个样本，每个样本有$d$维属性.一般情况下这个矩阵的大多数元素不为零，称之为稠密的.
   稀疏表示的含义是，寻找一个系数矩阵$A=\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\}\in R^{k\times n}$以及一个字典矩阵$B\in R^{d\times k}$，使得$BA$尽可能的还原$X$，且$A$尽可能稀疏，则$A$就为$X$的稀疏表示.
2. 字典学习
   为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表达形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为"字典学习"（dictionary learning）.
   目标函数：
   $$\underset{B,{\alpha }_i}{\min }\sum _{i=1}^m{\Vert x_i-B{\alpha }_i\Vert }_2^2+\lambda \sum _{i=1}^m{\Vert {\alpha }_i\Vert }_1$$
   其中，$x_i$为第$i$个样本，$B$为字典矩阵，${\alpha }_i$为$x_i$的稀疏表示，$\lambda$为大于0的参数。

上式中第一个累加项说明了字典学习的第一个目标是字典矩阵与稀疏表示的线性组合尽可能的还原样本；第二个累加项说明了alphai应该尽可能的稀疏。之所以用L1范式是因为L1范式正则化更容易获得稀疏解。
求解过程中：对字典$B$以及样本稀疏表示${\alpha }_i$交替迭代优化。即先初始化字典$B$，(1)固定字典$B$对${\alpha }_i$进行优化；(2)固定$A$对字典$B$进行优化。重复上述两步，求得最终$B$以及$X$的稀疏表示$A$。
其中第一步可采用与LASSO正则化相似的方法进行求解，第二步可采用KSVD方法进行求解。

算法模型

算法思路

传统的ZSL，思路就是建立一个语义空间，可以人工建立属性也可通过词嵌入模型构建，然后建立训练数据点到该空间的映射，然后测试样本也通过这个映射到语义空间再结合最近邻方法输出预测，但是已经通过实验证实这样直接将训练得到的映射给测试样本用存在domain shift问题，本文通过一个domain adaptation的框架以及结合传统的字典学习解决这个问题。

设定

定义符号：将训练样本集称为source domain（源域），测试样本集称为target domain, 样本所在 的视觉特征空间维度为 $d$, 语义空间维度为 $m,m<d;$ 有 $c_s$ 个可见类，共 $n_s$ 个样本, 所 有可见样本的类标签为 $z_s\in R^{n_s};c_t$ 个不可见类, $n_t$ 个样本，所有不可见样本的类标签为 $z_t\in R^{n_t};$ 将所有写成矩阵形式就是： $X_s\in R^{d\times n_s},X_t\in R^{d\times n_t},$ 其在语义空间中的对
应语义向量组成矩阵为 $Y_s\in R^{m\times n_s},Y_t\in R^{m\times n_t}$ (未知) $,$ 对于source domain的字典为 $D_s,$ 对于target domain的字典为 $D_t,$ 都是 $d\times m$ 维的, $d_i$ 为 $D$ 的第 $i$ 列。

算法原理

传统的字典学习包含字典矩阵$B$以及稀疏表示矩阵$A$两个变量，通过迭代的方式，轮流优化，来学习得到参数。在本文中对源域和目标域分开学习：

1. 源域source domain：
   $$D_s^{\ast }={\mathrm{argmin}}_{D_s}{\Vert X_s-D_s{Y}_s\Vert }_F^2$$
   s.t. $\forall i{\Vert d_i\Vert }_2^2\le 1$
   这是标准的形式，再加上正则化项：
   $$D_s^{\ast }={\mathrm{argmin}}_{D_s}{\Vert X_s-D_s{Y}_s\Vert }_F^2+{\lambda }_1{\Vert D_s\Vert }_F^2$$
   s.t. $\forall i{\Vert d_i\Vert }_2^2\le 1$
   这个形式就和ridge regression很相似了， 这也区分于传统的字典稀疏学习，因为这里只有一个优化变量 $D_s$
2. target domain: $$\left\{D_t^{\ast },Y_t^{\ast }\right\}={\mathrm{argmin}}_{D_t,Y_t}{\Vert X_s-D_t{Y}_t\Vert }_F^2+{\lambda }_2{\Vert Y_t\Vert }_1$$
   $$s.t.\forall i,{\Vert d_i\Vert }_2^2\le 1$$
   这里就是标准的字典稀疏学习的形式了，但是再观察这个式子，对于两个优化变量，仅仅是促使了 $Y_t$ 变的稀疏（1-范数约束），而没有保证学习得到的 $D_t$ 对于 $X_t$ 是正确的投影.再再目标函数上加上几个正则化项，才能让学到的 $D_t$ 和 $Y_t$ 更有 用。
   改写为：
   $$\left\{D_t^{\ast },Y_t^{\ast }\right\}={\mathrm{argmin}}_{D_t,Y_t}{\Vert X_s-D_t{Y}_t\Vert }_F^2+{\lambda }_2{\Vert Y_t\Vert }_1+{\lambda }_3{\Vert D_t-D_s\Vert }_F^2+{\lambda }_4\sum _{i,j}{w}_{ij}{\Vert y_i-p_j^t\Vert }_2^2$$
   $$s.t.\forall i{\Vert d_i\Vert }_2^2<1$$
   其中，$p_i^t$代表未见类$i$ 在语义空间的prototype
   新添加的两个正则化项：
   其中 ${\Vert D_t-D_s\Vert }_F^2$ 以 $D_s$ 为基础约束 $D_t$ (毕竟两个都是映射到同一个语义空间，这也就是相当于将 $D_s$ 作为先验知识，结合了传统的寻找视觉特征映射方法。
   而 ${\sum }_{i,j}{w}_{ij}{\Vert y_i-p_j^t\Vert }_2^2$，对于每个数据点学到的$y_i$，其对应的类标签为$z_t^i$,而该标签在语义空间的prototype为 $p_t^i$, 因此两者做一个误差项 ${\Vert y_i-p_j^t\Vert }_2^2$; $w_{ij}=p\left(z_t^j\mid x_i\right)$ 这个值可以通过IAP (indirect attribute prediction) 求出来，两者相乘再求和跑遍所有样本和类，结合了传统的视觉-语义相似度匹配方法。
   实验也证明了这两个额外的正则化项提高的模型的分类能力
   接下去就是和传统的字典学习差不多了，轮流固定，优化另一个，因为一起优化的话就是非凸问题了。

参考文献

[1]E. Kodirov, T. Xiang, Z. Fu, and S. Gong, ‘Unsupervised Domain Adaptation for Zero-Shot Learning’, in 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, Dec. 2015, pp. 2452–2460, doi: 10.1109/ICCV.2015.282.