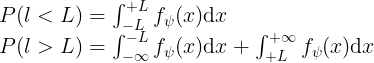Making a Difference to Differential Evolution
0、论文背景
差分进化(Differential Evolution)和进化规划(Evolutionary Programming)是进化计算中的两种主要算法。它们已成功地应用于许多真实世界的数值优化问题。社区搜索(Neighborhood Search)是支撑EP的主要策略，目前已经对不同的NS操作符(高斯随机数和柯西随机数)的特征进行了分析。虽然DE可能与EP的进化过程相似，但它缺乏邻域搜索的相关概念。本章提出了基于邻域搜索的NSDE。NSDE中的NS操作符可以显著提高NSDE的搜索步长和种群的多样性，而不依赖于任何关于搜索空间的先验知识 。
Yang Z, Yao X, He J. Making a difference to differential evolution[M]//Advances in metaheuristics for hard optimization. Springer, Berlin, Heidelberg, 2007: 397-414.
1、EP
进化规划(EP)进行的优化可以归纳为两个主要步骤：首先突变当前种群中的解，然后从突变的解和当前的解中选择下一代。
传统进化规划(CEP)的突变过程如下：
其中，
，
是种群大小；
，n是种群变量维度。上述也称古典进化规划(CEP)。
将柯西突变代替高斯突变，得到了快速进化规划(FEP)：
其中，对于每一个个体的每一维变量，
是一个尺度参数t=1的柯西随机变量。使用柯西突变的EP被称为快速进化规划(FEP)。
2、NSDE
有关DE，参见博客：DE，有关柯西分布，参见博客：柯西分布。
DE的流程如下：
有n维向量
，
，NP是种群的大小。
第一步：变异。
![\large i, i_{1}, i_{2}, i_{3} \in[1, N P]](http://img.e-com-net.com/image/info8/870c612a37ff4d9b9db7bc035bcc601d.gif){kind=small}
一个较大的F值会增加逃离局部最优的概率。然而，它也增加了突变的扰动，从而降低了DE的收敛速度。
第二步：交叉。
第三步：选择。
而本文提出的NSDE，与之前DE唯一不同的地方在于变异这一过程。DE中固定的常量变为了NS操作符(高斯随机数和柯西随机数)：
为什么要采用NS操作符代替F呢？简而言之：显著提高NSDE的搜索步长和种群的多样性，而不依赖于任何关于搜索空间的先验知识 。最终达到寻得更好的全局最优值以及加快收敛的目的。
那么高斯随机数和柯西随机数有什么特点呢？
就是各自的概率密度函数。
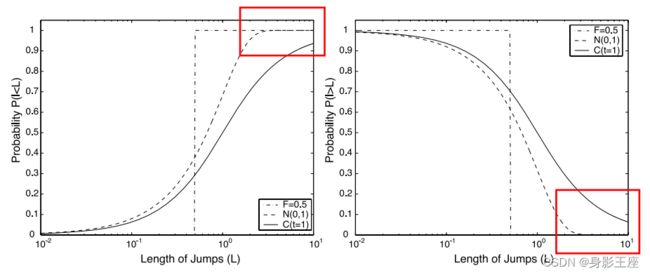
柯西随机数与高斯随机数最大的不同在于，柯西随机数产生的值范围更广，产生较大值的概率比高斯随机数高；而高斯随机数产生的值范围较窄，相对局部。
所以一般情况下，柯西算子在远离全局最优时表现更好，而高斯算子在一个较好的区域内寻找局部最优时表现更好。而为了结合上述二者的特点，由此提出了上述变异等式。
3、算法的个人实现以及简单实验
DE的实现上述DE有关的博客有提到过，就不展示了。
NSDE代码实现：
function [globalBest, globalBestFitness, FitnessHistory] = NSDE(popsize, maxIteration,dim, LB, UB, CR, Fun)
% 种群的初始化和计算适应度值
Sol(popsize, dim) = 0; % Declare memory.
Fitness(popsize) = 0;
for i = 1:popsize
Sol(i,:) = LB+(UB-LB).* rand(1, dim);
Fitness(i) = Fun(Sol(i,:));
end
% 获得全局最优值以及对应的种群向量
[fbest, bestIndex] = min(Fitness);
globalBest = Sol(bestIndex,:);
globalBestFitness = fbest;
% 开始迭代
for time = 1:maxIteration
for i = 1:popsize
% 突变
r = randperm(popsize, 3); %在1~pop中随机选择5个数组成一个数组
r1 = rand();
if r1 > 0.5
pd = makedist('tLocationScale','mu',0,'sigma',1,'nu',1);
F = random(pd,1,1);%生成1个柯西随机数
else
F = normrnd(0.5,0.5);%生成1个高斯随机数
end
mutantPos = Sol(r(1),:) + F * (Sol(r(2),:) - Sol(r(3),:));
% 交叉
jj = randi(dim); % 选择至少一维发生交叉
for d = 1:dim
if rand() < CR || d == jj
crossoverPos(d) = mutantPos(d);
else
crossoverPos(d) = Sol(i,d);
end
end
% 检查是否越界.
crossoverPos(crossoverPos>UB) = UB(crossoverPos>UB);
crossoverPos(crossoverPos进行简单的实验：
clear;clc;clearvars;
% 初始化变量维度,种群数,最大迭代次数,搜索区间,F,CR
dim = 20;
popsize = 100;
maxIteration = 1000;
LB = -5.12 * ones(1, dim);
UB = 5.12 * ones(1, dim);
F = 1;
CR = 0.9;
[globalBest, globalBestFitness, FitnessHistory] = DE(popsize, maxIteration,dim, LB, UB, F, CR, @(x)Rastrigin(x));
[globalBest1, globalBestFitness1, FitnessHistory1] = NSDE(popsize, maxIteration,dim, LB, UB, CR, @(x)Rastrigin(x));
plot(FitnessHistory);
hold on;
plot(FitnessHistory1);
legend('DE','NSDE','Location', 'northeast');
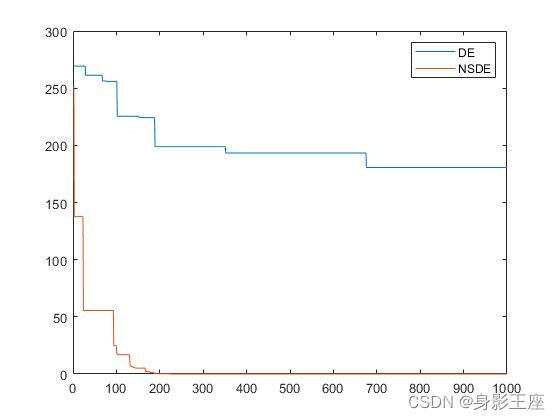
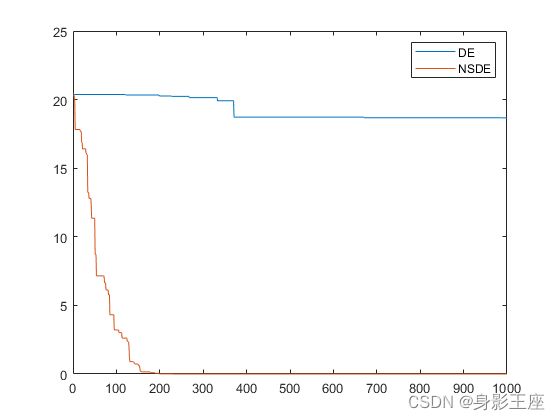
Rastrigin函数的测试结果：
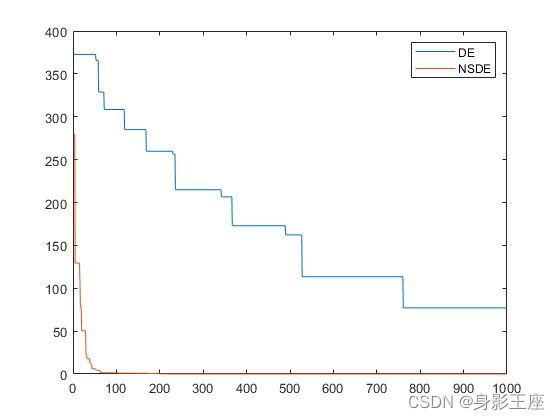
Grtiewank函数的测试结果：
Ackley函数的测试结果：
综上所述，NSDE无论在优化效果上，还是在收敛性上，均远远优于DE。
如有错误，还望批评改正，