（最新版2022版）剑指offer之排序题解

---

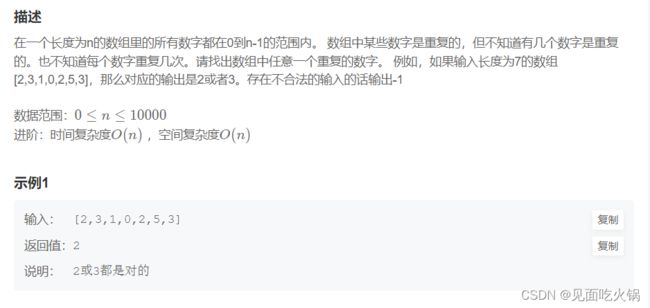
JZ3数组中重复的数字

思路：

既然数组长度为nnn只包含了0到n−1n-1n−1的数字，那么如果数字没有重复，这些数字排序后将会与其下标一一对应。那我们就可以考虑遍历数组，每次检查数字与下标是不是一致的，一致的说明它在属于它的位置上，不一致我们就将其交换到该数字作为下标的位置上，如果交换过程中，那个位置已经出现了等于它下标的数字，那肯定就重复了。

具体做法：

• step 1：遍历数组，遇到数组元素与下标相同的不用管。
• step 2：遇到数组元素与下标不同，就将其交换到属于它的位置，交换前检查那个位置是否有相同的元素，若有则重复。
• step 3：遍历结束完全交换也没重复，则返回-1.

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param numbers int整型一维数组
     * @return int整型
     */
    public int duplicate (int[] numbers) {
        // write code here
        for (int i = 0; i < numbers.length; i++) {
            //下标和对应的下标元素值不等，则交换
            while (i != numbers[i]) {
                //交换前，i位置元素已经等于numbers[i]位置元素
                if (numbers[i] == numbers[numbers[i]]) {
                    return numbers[i];
                }

                int temp = numbers[numbers[i]];
                numbers[numbers[i]] = numbers[i];
                numbers[i] = temp;
            }

        }
        return -1;
    }
}

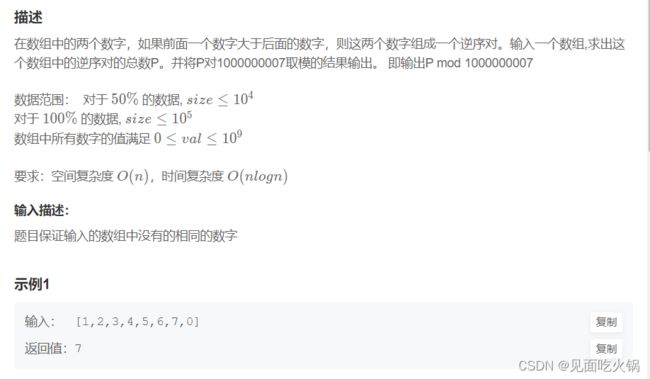
JZ51 数组中的逆序对

思路：
因为我们在归并排序过程中会将数组划分成最小为1个元素的子数组，然后依次比较子数组的每个元素的大小，依次取出较小的一个合并成大的子数组。

//取中间
int mid = (left + right) / 2;
//左右划分合并
merge(divide(left, mid, data, temp), divide(mid + 1, right, data, temp));

这里我们也可以用相同的方法划分，划分之后相邻一个元素的子数组就可以根据大小统计逆序对，而不断往上合并的时候，因为已经排好序了，我们逆序对可以往上累计。我们主要有以下三个阶段。

具体做法：

• step 1： 划分阶段：将待划分区间从中点划分成两部分，两部分进入递归继续划分，直到子数组长度为1.
• step 2： 排序阶段：使用归并排序递归地处理子序列，同时统计逆序对，因为在归并排序中，我们会依次比较相邻两组子数组各个元素的大小，并累计遇到的逆序情况。而对排好序的两组，右边大于左边时，它大于了左边的所有子序列，基于这个性质我们可以不用每次加1来统计，减少运算次数。
• step 3： 合并阶段：将排好序的子序列合并，同时累加逆序对。

public class Solution {
    int count = 0;
    public int InversePairs(int [] array) {
        if (array == null || array.length <= 1) {
            return 0;
        }

        //先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        int[] temp = new int[array.length];
        mergeSort(array, 0, array.length - 1, temp);
        return count;
    }

    private void mergeSort(int[] array, int left, int right, int[] temp) {
        if (left == right) {
            return;
        }

        int mid = left + (right - left) / 2;
        //左边归并排序，使得左子序列有序
        mergeSort(array, left, mid, temp);
        //右边归并排序，使得右子序列有序
        mergeSort(array, mid + 1, right, temp);
        //将两个有序子数组合并操作
        merge(array, left, mid, right, temp);
    }

    //mid代表左半边的最后一个元素位置
    private void merge(int[] array, int left, int mid, int right, int[] temp) {
        //指向左边的第一个位置
        int i = left;
        //指向右边的第一个位置
        int j = mid + 1;
        //指向临时数组的第一个位置
        int k = 0;

        while (i <= mid && j <= right) {
            if (array[i] > array[j]) {
                temp[k++] = array[j++];
                count = (count + mid - i + 1) % 1000000007;
            } else {
                temp[k++] = array[i++];
            }
        }

        //将左边剩余元素填充进temp中
        while (i <= mid) {
            temp[k++] = array[i++];
        }

        //将右序列剩余元素填充进temp中
        while (j <= right) {
            temp[k++] = array[j++];
        }

        k = 0;
        //将temp中的元素全部拷贝到原数组中
        while (left <= right) {
            array[left++] = temp[k++];
        }
    }
}

JZ40 最小的K个数

思路：

要找到最小的k个元素，只需要准备k个数字，之后每次遇到一个数字能够快速的与这k个数字中最大的值比较，每次将最大的值替换掉，那么最后剩余的就是k个最小的数字了。

如何快速比较k个数字的最大值，并每次替换成较小的新数字呢？我们可以考虑使用优先队列（大根堆），只要限制堆的大小为k，那么堆顶就是k个数字的中最大值，如果需要替换，将这个最大值拿出，加入新的元素就好了。

//较小元素入堆
if(q.peek() > input[i]){
	q.poll();
	q.offer(input[i]);
}

具体做法：

• step 1：利用input数组中前k个元素，构建一个大小为k的大顶堆，堆顶为这k个元素的最大值。
• step 2：对于后续的元素，依次比较其与堆顶的大小，若是比堆顶小，则堆顶弹出，再将新数加入堆中，直至数组结束，保证堆中的k个最小。
• step 3：最后将堆顶依次弹出即是最小的k个数。

import java.util.*;

public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList<Integer> list = new ArrayList<>();
        if (input.length == 0 || k == 0) {
            return list;
        }

        // o1 - o2为小顶堆，o2-o1为大顶堆
        PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> o2 - o1);

        for (int i = 0; i < input.length; i++) {
            queue.add(input[i]);
            if (queue.size() > k) {
                queue.poll();
            }
        }

        while (!queue.isEmpty()) {
            list.add(0, queue.poll());
        }
        return list;
    }
}

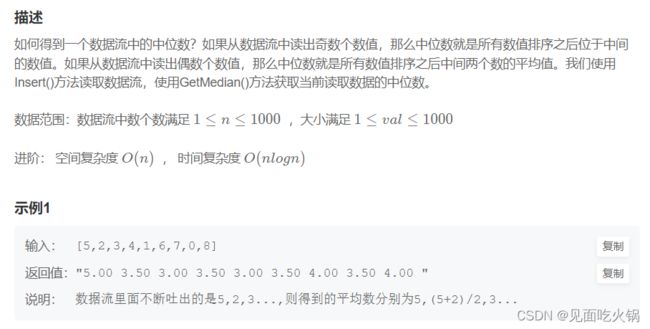
JZ41 数据流中的中位数

思路：

除了插入排序，我们换种思路，因为插入排序每次要遍历整个已经有的数组，很浪费时间，有没有什么可以找到插入位置时能够更方便。

我们来看看中位数的特征，它是数组中间个数字或者两个数字的均值，它是数组较小的一半元素中最大的一个，同时也是数组较大的一半元素中最小的一个。那我们只要每次维护最小的一半元素和最大的一半元素，并能快速得到它们的最大值和最小值，那不就可以了嘛。这时候就可以想到了堆排序的优先队列。

具体做法：

• step 1：我们可以维护两个堆，分别是大顶堆min，用于存储较小的值，其中顶部最大；小顶堆max，用于存储较大的值，其中顶部最小，则中位数只会在两个堆的堆顶出现。
• step 2：我们可以约定奇数个元素时取大顶堆的顶部值，偶数个元素时取两堆顶的平均值，则可以发现两个堆的数据长度要么是相等的，要么奇数时大顶堆会多一个。
• step 3：每次输入的数据流先进入大顶堆排序，然后将小顶堆的最大值弹入大顶堆中，完成整个的排序。
• step 4：但是因为大顶堆的数据不可能会比小顶堆少一个，因此需要再比较二者的长度，若是小顶堆长度小于大顶堆，需要从大顶堆中弹出最小值到大顶堆中进行平衡。

import java.util.*;
public class Solution {
    //小顶堆，存放较大的数
    PriorityQueue<Integer> min = new PriorityQueue<>();
    //大顶堆，存放较小的数
    PriorityQueue<Integer> max = new PriorityQueue<>((o1, o2) -> o2 - o1);
    public void Insert(Integer num) {
        //要加入的数为第奇数个
        if(max.size() == min.size()){
            max.add(num);
            min.add(max.poll());
        //要加入的数为第偶数个
        }else{
            min.add(num);
            max.add(min.pol1l());
        }
    }

    public Double GetMedian() {
        if(max.size() == min.size()){
            return (min.peek() + max.peek()) / 2.0;
        }else{
            return min.peek() * 1.0;
        }
    }
    
}