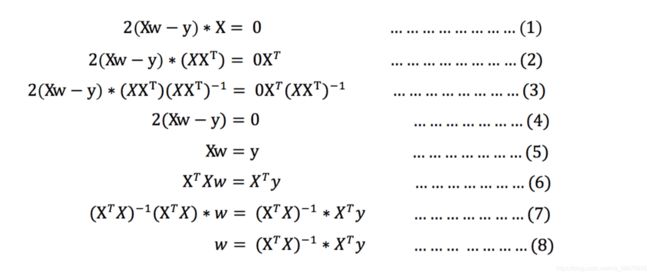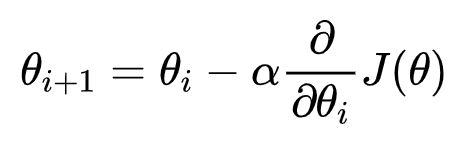机器学习:线性回归之损失函数、正规方程、梯度下降、过拟合和欠拟合、正则化
1.线性回归
1.1 定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
通用公式:
h ( w ) = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = W T X + b h(w)=w_1x_1+w_2x_2+\cdots+w_nx_n+b=W^TX+b h(w)=w1x1+w2x2+⋯+wnxn+b=WTX+b
-
w 叫做特征权重
-
x 叫做特征值
-
b 叫做偏置
其 中 W 、 X 可 以 理 解 为 矩 阵 : W = ( w 0 w 1 w 2 w 3 ⋯ ) , X = ( x 0 x 1 x 2 x 3 ⋯ ) 其中W、X可以理解为矩阵:W = \left( \begin{matrix} \ w_0 \\ \ w_1 \\ \ w_2 \\ \ w_3 \\ \ \cdots \end{matrix} \right),X = \left( \begin{matrix} \ x_0 \\ \ x_1 \\ \ x_2 \\ \ x_3 \\ \ \cdots \end{matrix} \right) 其中W、X可以理解为矩阵:W=⎝⎜⎜⎜⎜⎛ w0 w1 w2 w3 ⋯⎠⎟⎟⎟⎟⎞,X=⎝⎜⎜⎜⎜⎛ x0 x1 x2 x3 ⋯⎠⎟⎟⎟⎟⎞ -
默认将w0x0 = b
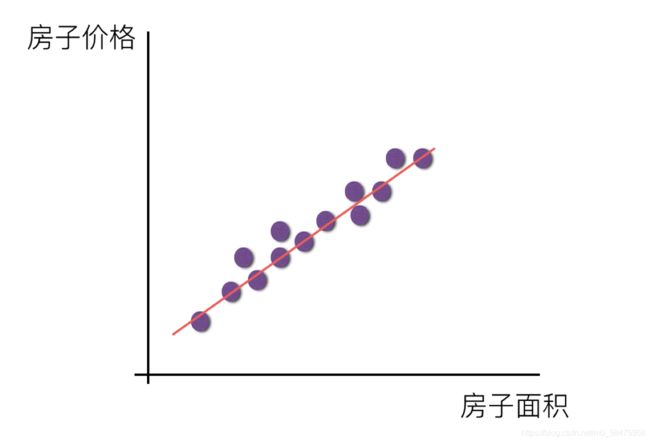
1.2 线性回归的特征与目标的关系分析
线性回归当中主要有两种模型,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征或两个特征举例子。
注释:单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
注释:为什么会这样的关系呢?原因是什么?
如果是非线性关系,那么回归方程可以理解为多幂次函数
2.损失函数理解
对于上述的线性回归公式,向量 x 表示样本为已知值,而 w、b 则是模型的参数,是未知的。我们的目标则是根据已知训练集去求解合适的 w、b 参数值。
对于 w、b 参数的组合有无数种,那么也就存在无数条直线能够拟合数据集。此时,就需要损失函数来评估那条直线是我们想要的。
损失函数,是用来衡量模型优劣的一个函数。从损失函数入手,即可得到最佳的 w、b 参数的值。
现在,我们要去定义一个损失函数。经过思考,我们发现模型预测的结果和真实结果之间差距越小,则模型拟合效果越好。
2.1 损失函数公式
J ( f ( x ) , y ) = 1 2 ∑ i = 1 n ( f ( x i ) − y i ) 2 J(f(x),y)=\frac{1}{2}\sum_{i=1}^n(f(x_i)-y_i)^2 J(f(x),y)=21i=1∑n(f(xi)−yi)2
- yi 表示真实结果
- f(xi) 表示预测结果
- 又称最小二乘法:最小化误差平方和求得模型参数。
我们计算所有样本的预测值和真实值的差距,取总差距最小的直线作为最终的直线(模型)。此时,最优的 w、b 的值我们就得到了。
损失函数:用于衡量模型能力。
2.2 优化算法
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
- 正规方程:可以直接求解,准确的结果。
- 梯度下降法:通过迭代的方式一步一步的计算 w、b,近似最优解
2.2.1 正规方程
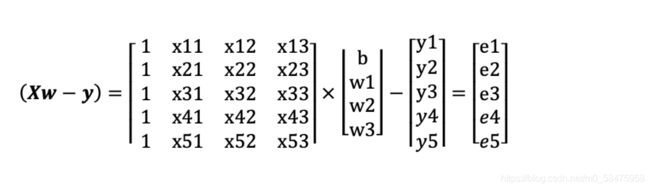
我们用 X 代表所有的样本,w (列向量)代表样本特征的权重,损失函数公式可以修改为:
J ( w ) = ( X w − y ) 2 J(w)=(Xw-y)^2 J(w)=(Xw−y)2
(1)令 Xw -y 为 N, 则:
(2)N2 的导数为:2N * N 的导数
(3)2(Xw -y)*X(w1, w2, w3…) = 2(Xw -y)*X(1, 1, 1…) = 2(Xw -y)*X
公式推导过程:
- 任何一个矩阵乘以单位矩阵等于矩阵自身
- M矩阵xN矩阵 不一定等于 N矩阵xM矩阵
推导注释:
(1)对损失函数求导得到的。
(2)XXT 先让 X 变成方阵,方便将其转换为单位矩阵
(3)(XXT)(XXT)-1 得到单位矩阵
(4)约掉 X 之后的式子
(5)约掉 2,将 y 放到等号右侧
(6)再将 X 变成方阵,方便计算其单位矩阵
(7)将单位矩阵约掉
(8)求解到最后 w 向量的计算公式
注意:w 向量是(w0, w1, w2… wn),其中 w0 就是偏置 b, w1 开始就是每一个权重值。
正规方程公式:
W = ( X X T ) − 1 X T Y W=(XX^T)^{-1}X^TY W=(XXT)−1XTY
- 如果特征X特征特别多,用正规方程求解权重和偏置,计算量非常大,因此正规方程不适合大数据量的场景。
- 因为正规方程是一步计算到位,因此正规方程容易受到异常值的影响,导致最终的结果离真实结果偏差较大。不能在计算过程中对其进行影响,造成过拟合。
2.2.2梯度下降(Gradient Descent)
2.2.2.1 什么是梯度下降
梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景:
一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。
因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。
具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,(同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走)。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
首先,我们有一个可微分的函数。这个函数就代表着一座山。
我们的目标就是找到这个函数的最小值,也就是山底。
根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数值变化最快的方向。 所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
2.2.2.2 梯度的概念
梯度是微积分中一个很重要的概念
-
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率;
-
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向;
-
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
-
这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的反方向一直走,就能走到局部的最低点!
2.2.2.3 梯度下降公式
- α: 学习率(步长). 不能太大 也 不能太小.
- 梯度是上升最快的方向, 我们需要是下降最快的方向, 所以需要加负号
α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大,其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!
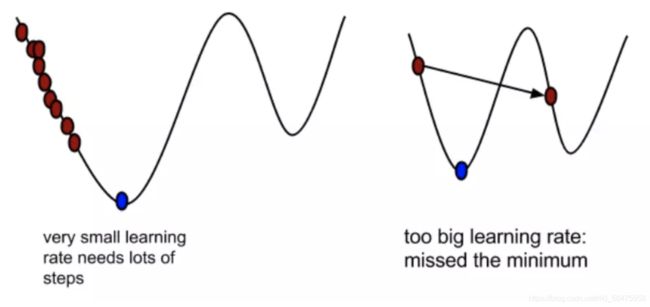
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号
2.2.2.4 梯度下降优化过程
- 给定初始位置、步长
- 计算该点当前的上升最快的负方向
- 向该负方向移动步长
- 重复 2-3 步 直至收敛
- 两次差距小于指定的阈值
- 达到指定的迭代次数
例如(单变量):
函数:J(θ) = θ2, 求当 θ 为何值时,J(θ) 值最小
J(θ) 函数关于 θ 的导数为: 2θ
初始化:
- 起点为: 1
- 学习率:α = 0.4
我们开始进行梯度下降的迭代计算过程:
第一步:θ = 1
第二步:θ = θ - α * (2θ) = 1 - 0.4 * 2 = 0.2
第三步:θ = θ - α * (2θ) = 0.2 - 0.4 * 0.4 = 0.04
第四步:θ = θ - α * (2θ) = 0.04 - 0.4 * 0.08 = 0.008
第五步:θ = θ - α * (2θ) = 0.008 - 0.4 * 0.016 = 0.0016
…
第N步:θ 已经极其接近最优值 0,J(θ) 也接近最小值。
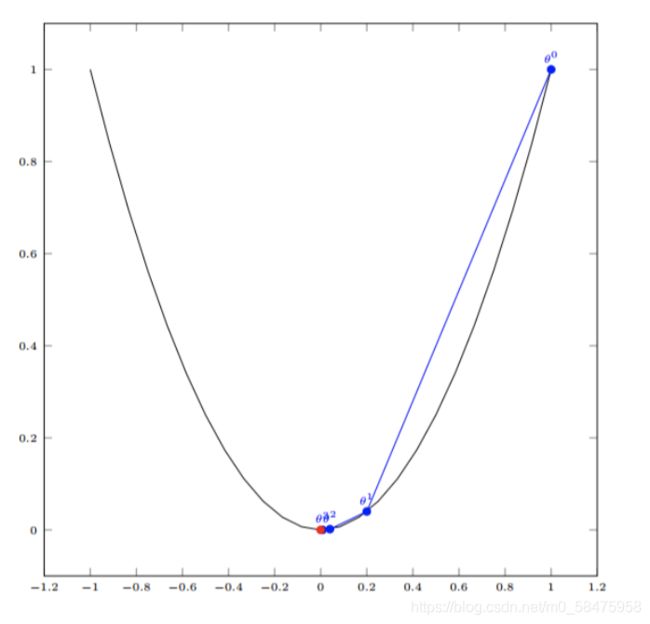
例子(多变量):
函数:J(θ) = θ12 + θ22,求 θ1、θ2 为何值时,J(θ) 的值最小
J(θ) 函数关于 θ1 的导数为: 2θ1
J(θ) 函数关于 θ2 的导数为: 2θ2
则 J(θ) 的梯度为:(2θ1, 2θ2)
初始化:
起点为: (1, 3)
学习率为:α = 0.1
我们开始进行梯度下降的迭代计算过程:
第一步:(θ1, θ2) = (θ1, θ2) - α * (2θ1, 2θ2) = (θ1-α*2θ1, θ1-α*2θ1) = (1-0.1*2, 3-0.1*6)=(0.8, 2.4)
第二步:(θ1, θ2) = (θ1, θ2) - α * (2θ1, 2θ2) = (θ1-α*2θ1, θ1-α*2θ1) = (0.8-0.1*1.6, 2.4-0.1*4.8)=(0.64, 1.92)
…
第N步: θ1、θ2 已经极其接近最优值,J(θ) 也接近最小值。
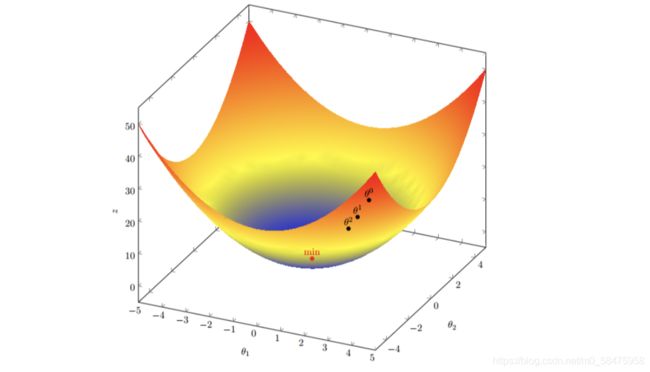
注意:通过梯度下降求出的w、b不能保证是全局最优权重和偏置,只能作为当前局部内最优权重和偏置。例如下图: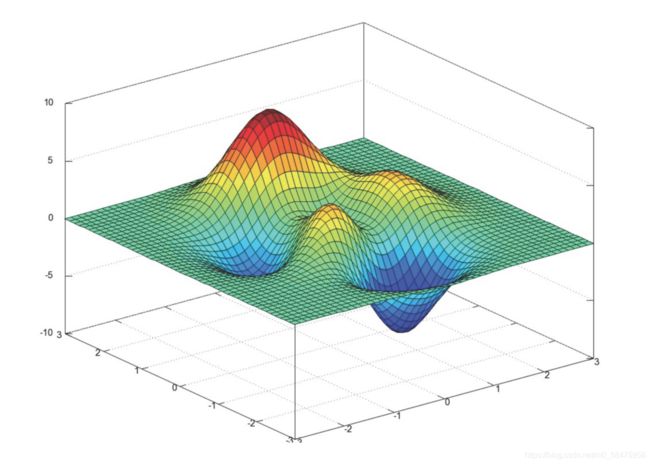
通过给出不同的起点和学习率,最低点有可能在左边,也有可能在右边,所以只能说梯度下降只能是局部最优。
优化动态图显示:
2.2.2.5 梯度下降公式推导
步骤:
- 确认优化模型的假设函数和损失函数
- 算法相关参数初始化,例如:权重、偏置初始值、学习率
- 使用梯度下降公式,迭代求解模型参数(权重、偏置)
损失函数求导:
均方误差
参数更新公式:
w = w − α ⋅ 1 m ∑ i = 1 m ( f ( x i ) − y i ) w= w-\alpha\cdot\frac{1}{m}\sum_{i=1}^m(f(x_i)-y_i) w=w−α⋅m1i=1∑m(f(xi)−yi)
注意: w 每次更新需要使用所有样本的梯度值。
2.2.2.6 其他梯度下降算法
-
全梯度下降算法(FGD)
- 每次迭代时, 使用全部样本的梯度值
-
随机梯度下降算法(SGD)
- 每次迭代时, 随机选择并使用一个样本梯度值
-
小批量梯度下降算法(mini-bantch)
- 每次迭代时, 随机选择并使用小批量的样本梯度值
-
随机平均梯度下降算法(SAG)
-
每次迭代时, 随机选择一个样本的梯度值和以往样本的梯度值的均值
-
假设: 训练集有 A B C D E F G H 共 8 个样本
- 随机选择一个样本,假设选择 D 样本,计算其梯度值并存储到列表:[D],然后使用列表中的梯度值均值,更新模型参数。
- 随机再选择一个样本,假设选择 G 样本,计算其梯度值并存储到列表:[D, G],然后使用列表中的梯度值均值,更新模型参数。
- 随机再选择一个样本,假设又选择了 D 样本, 重新计算该样本梯度值,并更新列表中 D 样本的梯度值,使用列表中梯度值均值,更新模型参数。
- …以此类推,直到算法收敛。
-
结论:
- 全梯度下降:由于使用全部数据集,训练速度较慢
- 随机梯度下降:综合虑迭代次数和运行时间,SG表现性能都很好,能在训练初期快速摆脱初始梯度值,快速将平均损失函数降到很低。但要注意,在使用SG方法时要慎重选择步长,否则容易错过最优解。
- 小批量梯度下降:结合了 SG 的胆大和 FG 的心细,它的表现也正好居于 SG 和 FG 二者之间。目前使用最多,正是因为它避开了 FG 运算效率低成本大和 SG 收敛效果不稳定的缺点。
- 随机平均梯度下降:训练初期表现不佳,优化速度较慢。这是因为我们常将初始梯度设为0,而 SAG 每轮梯度更新都结合了上一轮梯度值。
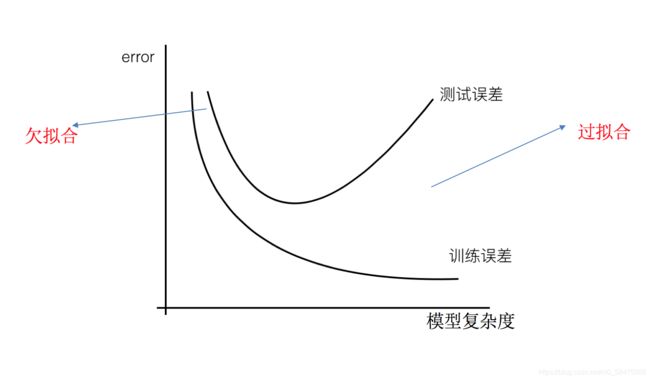
3.过拟合和欠拟合
3.1 过拟合
- 一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
- 原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法:
- 重新清洗数据
- 增大数据的训练量
- 正则化
- 减少特征维度,防止维灾难
3.2 欠拟合
-
一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
-
原因:学习到数据的特征过少
-
解决办法:
- 添加其他特征项
- 添加多项式特征,这个在机器学习算法里面用的很普遍,将线性模型通过添加二次项或者三次项使模型泛化能力更强。
3.3 正则化
在模型训练时,数据中有些特征影响模型复杂度、或者某个特征的异常值较多,所以要尽量减少这个特征的影响(甚至删除某个特征的影响),这就是正则化。
注:调整时候,算法并不知道某个特征影响,而是去调整参数得出优化的结果
3.3.1 L1正则化
J ( w ) = M S E ( w ) + α ∑ i = 1 n ∣ w i ∣ J(w)=MSE(w)+\alpha\sum_{i=1}^n|w_i| J(w)=MSE(w)+αi=1∑n∣wi∣
-
MSE(w):均方误差
-
L1 正则化会使得权重趋向于 0,甚至等于 0,使得某些特征失效,达到特征筛选的目的
-
使用 L1 正则化的线性回归模型是 Lasso 回归
-
α 叫做惩罚系数,该值越大则权重调整的幅度就越大,即:表示对特征权重惩罚力度就越大。
3.3.2 L2正则化
J ( w ) = M S E ( w ) + α ∑ i = 1 n w i 2 J(w)=MSE(w)+\alpha\sum_{i=1}^nw_i^2 J(w)=MSE(w)+αi=1∑nwi2
- L2 正则化会使得权重趋向于 0,一般不等于 0
- 使用 L2 正则化的线性回归模型是岭回归。
- α 叫做惩罚系数,该值越大则权重调整的幅度就越大,即:表示对特征权重惩罚力度就越大。
3.4 维灾难
随着维度的增加,分类器性能逐步上升,到达某点之后,其性能便逐渐下降。
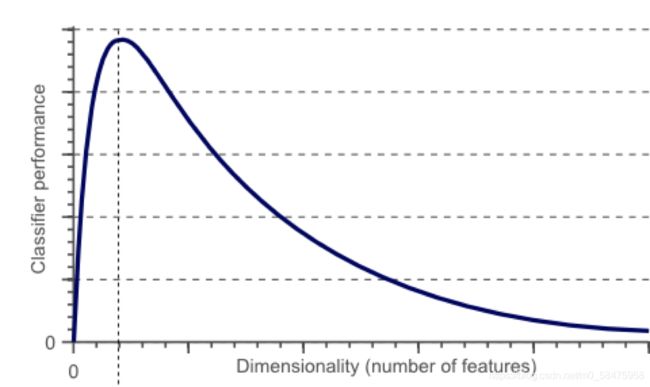
原因:随着维度的增加,相对样本数量将变得越来越少。虽然能够对训练样本很好分类,但由于特征多,样本数量少,导致学习不充分,泛化能力差。
4.正则化线性模型
4.1 Ridge Regression (岭回归,又名 Tikhonov regularization)
岭回归是线性回归的正则化版本,即在原来的线性回归的 cost function 中添加正则项(regularization term):
α ∑ i = 1 n θ i 2 \alpha\sum_{i=1}^n\theta_i^2 αi=1∑nθi2
以达到在拟合数据的同时,使模型权重尽可能小的目的,岭回归代价函数:
KaTeX parse error: Can't use function '\)' in math mode at position 10: J(w)=MSE(\̲)̲+\alpha\sum_{i=…
即:
J ( θ ) = 1 m ∑ i = 1 m ( W T ⋅ X i − Y i ) 2 + α ∑ i = 1 n θ i 2 J(\theta)=\frac{1}{m}\sum_{i=1}^m(W^T\cdot X^i-Y^i)^2+\alpha\sum_{i=1}^n\theta_i^2 J(θ)=m1i=1∑m(WT⋅Xi−Yi)2+αi=1∑nθi2
- α=0:岭回归退化为线性回归
4.2 Lasso Regression(Lasso 回归)
Lasso 回归是线性回归的另一种正则化版本,正则项为权值向量的ℓ1范数。
Lasso回归的代价函数 :
J ( θ ) = M S E ( θ ) + α ∑ i = 1 n ∣ θ i ∣ J(\theta)=MSE(\theta)+\alpha\sum_{i=1}^n|\theta_i| J(θ)=MSE(θ)+αi=1∑n∣θi∣
【注意 】
- Lasso Regression 的代价函数在 θi=0处是不可导的.
- 解决方法:在θi=0处用一个次梯度向量(subgradient vector)代替梯度,如下式
Lasso Regression 的次梯度向量:
Lasso Regression 有一个很重要的性质是:倾向于完全消除不重要的权重。
例如:当α 取值相对较大时,高阶多项式退化为二次甚至是线性:高阶多项式特征的权重被置为0。
也就是说,Lasso Regression 能够自动进行特征选择,并输出一个稀疏模型(只有少数特征的权重是非零的)。
4.3 Elastic Net (弹性网络)
弹性网络在岭回归和Lasso回归中进行了折中,通过 混合比(mix ratio) r 进行控制:
r=0:弹性网络变为岭回归
r=1:弹性网络便为Lasso回归
弹性网络的代价函数 :
J ( θ ) = M S E ( θ ) + r α ∑ i = 1 n ∣ θ i ∣ + 1 − r 2 α ∑ i = 1 n θ 2 J(\theta)=MSE(\theta)+r\alpha\sum_{i=1}^n|\theta_i|+\frac{1-r}{2}\alpha\sum_{i=1}^n\theta^2 J(θ)=MSE(θ)+rαi=1∑n∣θi∣+21−rαi=1∑nθ2
一般来说,我们应避免使用朴素线性回归,而应对模型进行一定的正则化处理