Deep metric learning 深度度量学习 总结

最近的工作用是深度度量学习的改进，这里将DML进行一个总结。

根据个人的理解，开篇用一句话介绍一下度量学习：

“不同于分类学习，度量学习是通过学习数据之间的相似性程度来获得一个更有意义或者说更具可分性的特征空间。”

Traditional metric learning

核心目的：

1 通过一个optimal的距离度量来判断样本之间的相似性

2 减小相似样本之间的距离，增加不相似样本之间的距离

限制条件：往往利用的的是线性映射，导致很难解决实际问题中的non-linear问题。（当然大部分传统方法都会遇到这个问题，最常见的方法就是核方法，譬如SVM原本只能解决线性分类，但是加入高斯核或多项式核就可以解决非线性分类，还有PCA-KPCA这些）

Deep metric learning（DML）

通过深层结构，学习到高抽象化的非线性特征以及数据之间的相似性关系。

DML三大关键点： 采样策略、合适的距离度量函数以及模型结构，因此当前DML模型往往基于指定任务在这些方面进行改进。[1]

距离度量

度量学习希望学习到一种distance metric，使得在该distance metric下，相似数据（不相似数据）能够在空间中有更好的分布。最经典的就是利用马氏距离（Mahalanobis distance）,如下式，其中 $x_i\in R^m$
$$D(x_i,x_j)=\sqrt{(x_i-x_j{)}^{T}M(x_j-x_j)}$$
作为一个距离函数，那么一定要包含几个性质：非负、对称以及三角不等，如果想在度量上进行创新一定要注意这些。马氏距离中的$M$具有半正定和对称性，那么根据矩阵理论相关知识，$M$的特征值要全部非负，且存在n阶实矩阵$W$使得$M=W^{T}W$ ，则上述式子可以转化为：
$$\begin{gathered} D(x_i,x_j)=\sqrt{(x_i-x_j{)}^T{W}^{T}W(x_j-x_j)} \\ =\sqrt{[(x_i-x_j{)}^T{W}^T][W(x_j-x_j)]} \\ =\sqrt{(W{x}_i-W{x}_j{)}^T(W{x}_j-W{x}_j)} \\ =\Vert W{x}_i-W{x}_j\Vert \end{gathered}$$
OK，那从上面这个式子可以看到，原始空间的马氏距离就对应经过一个线性映射$W$之后新空间中的欧氏距离，也就是说基于马氏距离的度量学习其实就是学习一个$W$,经过这个矩阵的映射之后的数据点具有相似数据更近，不相似数据更远的特性。同时，学习的矩阵是一个线性映射，也就意味着仅用这种方式是无法解决非线性问题的，因此就要学习$ f(x)$， DML就是利用强大的特征学习能力，学习到这样一个映射。

采样

采样策略在DML中扮演着一个非常重要的角色，一个好的采样策略可以大大提升模型的效果以及计算速度。采样策略的发展如下：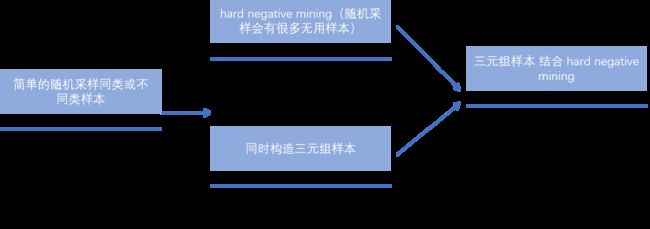
关于DML中采样策略发展历史中几个比较关键的节点

1 2006年 大神Lecun提出的孪生网络，其中采样是先随机选一个样本，然后0.5的概率从同类样本中随机采样，0.5的概率从不同类样本采样[2]

2 后来发现，很多简单的样本对学习模型并没有作用，因此提出了hard sample mining[3]

3 另一个经典DML模型三元组网络，同时选择anchor, positive sample和negative sample作为输入，同时考虑同类与异类的距离关系[4]

4 将三元组与hard sample mining结合。[5]

提到的hard negative sample是什么呢？

如上图所示，黑色点代表anchor 和 positive sample ， 橙色点 1 2 3 分别是negative sample，在采样的时候 如果我们选择3作为负例，其实对模型的学习是没有意义的，因为此时负例与anchor之间的距离已经大于正例与anchor之间的距离加上一个期望的margin（这就是随机采样，不考虑hard negative sample）。因此其实只有采样1 和 2才是真正有意义的，但还有一个问题是如果我们选择1，也就是 hard negative，出现的问题就是 后续的loss会很大，对应的梯度也会很大，模型会很难收敛。那么最好的采样就是2， 距离大于正例与anchor的距离，同时不超过一个期望的margin，那么模型学习起来就会轻松。

Loss function

这一节会介绍一些经典的DML中用到的loss function，排序按照提出的先后顺序。所用到的距离函数如下，其中G代表网络映射函数。
$$D(X_1,X_2)=\Vert G(X_1)-G(X_2)\Vert$$
1 Contrastive loss [2]

对比损失是Lecun 孪生网络论文中提到的损失函数，如前面提到的，采样是正负样本随机采样，如果是正采样则参数Y = 0 ,否则参数Y = 1. 损失函数如下：
$$Loss=(1-Y)\frac{1}{2}(D(X_1,X_2){)}^2+Y\frac{1}{2}{max(0,margin-D(X_1,X_2))}^2$$
该函数的目的是，当两个样本同类时，希望D减小，当两个样本异类时，希望D增加，同时如果D超过设定的margin，则不再进行模型更新。

2 Triplet loss [4]

三元损失如前面介绍的，同时选择anchor，positive 和 negative。损失函数如下：
$$Loss=max(0,D(X,X_p)-D(X,X_n)+a)$$
该损失函数同时考虑anchor 与 positive sample和 negative sample的距离关系，并且考虑的是相对距离关系，如果$D(X,X_n)>D(X,X_P)+a$, 参数就不会更新.

3 Angular loss [6]

角损失不同于前面两个损失，而是通过角度约束负例样本。
$$Loss=max(0,D(X,X_p)-4ta{n}^2\alpha D(X_n,X^c))$$
损失函数中$X^c$是正例样本的clustering center ，也就是说通过一种角度度量来限制负例样本和正例样本聚类中心的距离。

其他一些loss包括Quadruplet loss[7]通过再增加一个跟anchor接近的样本，实现四元组； Stuctured loss[8]利用了训练过程中的结构化信息（距离向量转化为距离矩阵）； N-pair Loss[9]利用多类别数据解决收敛慢和局部最优的问题…

参考文献

[1]Kaya, Bilge. Deep Metric Learning: A Survey. Symmetry. 2019;11(9):1066. doi:10.3390/sym11091066

[2]Hadsell, R.; Chopra, S.; LeCun, Y. Dimensionality Reduction by Learning an Invariant Mapping.
In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY,
USA, 17–22 June 2006; pp. 1735–1742.

[3]Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative learning of deep
convolutional feature point descriptors. In Proceedings of the IEEE International Conference on Computer
Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 118–126.

[4]Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Progress in Pattern Recognition, Image
Analysis, Computer Vision, and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9370,
pp. 84–92.

[5]Lin, Y.; Cui, Y.; Zhou, F.; Belongie, S. Fine-Grained Categorization and Dataset Bootstrapping Using Deep
Metric Learning with Humans in the Loop. In Proceedings of the IEEE International Conference on Computer
Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1153–1162

[6]Wang, J.; Zhou, F.; Wen, S.; Liu, X.; Lin, Y. Deep Metric Learning with Angular Loss. In Proceedings of the
IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2593–2601.

[7]Ni, J.; Liu, J.; Zhang, C.; Ye, D.; Ma, Z. Fine-grained Patient Similarity Measuring using Deep Metric Learning.
In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore,
6–10 November 2017; pp. 1189–1198.

[8]Song, H.O.; Savarese, S.; Xiang, Y.; Jegelka, S. Deep Metric Learning via Lifted Structured Feature Embedding.
In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV,
USA, 27–30 June 2016; pp. 4004–4012

[9]Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. In Proceedings of the Advances
in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 1857–1865