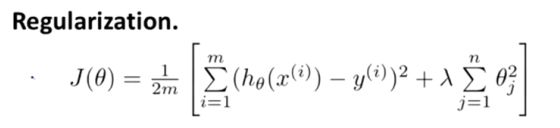今天阅读了一篇andrew ng的机器学习课程笔记,讲的是正则化。原文地址如下:http://doc.okbase.net/jianxinzhou/archive/111322.html
1. 过拟合
如果建立的模型没能很好地拟合训练数据,那么这种情况称为欠拟合(underfitting),或者叫作高偏差(bias)。
如果建立的模型对训练数据拟合得很好,但是泛化能力很差,即对于新数据的预测能力很差,那么这种情况就叫作过拟合(overfitting),也叫作高方差。
一般来说,如果没有足够大的数据集(训练集)去约束一个变量过多的模型,那么就会发生过拟合。
2.处理过拟合的两种方法
1)尽量减少选取变量的数量
具体而言,我们可以人工检查每一项变量,并以此来确定哪些变量更为重要,然后,保留那些更为重要的特征变量。至于,哪些变量应该舍弃,这会涉及到模型选择算法,这种算法是可以自动选择采用哪些特征变量,自动舍弃不需要的变量。这类做法非常有效,但是其缺点是当你舍弃一部分特征变量时,你也舍弃了问题中的一些信息。
2)正则化
正则化中我们将保留所有的特征变量,但是会减小特征变量的数量级(参数数值的大小θ(j))。
这个方法非常有效,当我们有很多特征变量时,其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样,我们可以有很多特征变量,其中每一个变量都是有用的,因此我们不希望把它们删掉,这就导致了正则化概念的发生。
因此,要在损失函数中加入惩罚项,也叫正则项,以线性回归为例:
按照惯例,这里没有去惩罚 θ0,因此 θ0 的值是大的。这就是一个约定从 1 到 n 的求和,而不是从 0 到 n 的求和。但在实践中,这只会有非常小的差异,无论你是否包括这 θ0 这项。但是按照惯例,通常情况下我们还是只从 θ1 到 θn 进行正则化。
包含λ的那一项就是正则项,λ称作正则化系数,它要做的就是控制在两个不同的目标中的平衡关系。
第一个目标就是我们想要训练,使假设更好地拟合训练数据。我们希望假设能够很好的适应训练集。
而第二个目标是我们想要保持参数值较小。(通过正则化项)
而 λ 这个正则化参数需要控制的是这两者之间的平衡,即平衡拟合训练的目标和保持参数值较小的目标。从而来保持假设的形式相对简单,来避免过度的拟合。
如果 λ 被设定为非常大,为了保证损失函数足够小,会使模型中的参数接近于0,从而出现欠拟合的现象。
因此,为了使正则化运作良好,我们应当注意一些方面,应该去选择一个不错的正则化参数 λ 。