词向量:GloVe 模型详解
本内容主要介绍构建词向量的 GloVe 模型。
1 前言
在 GloVe 模型被提出之前,学习词向量的模型主要有两大类:
- 全局矩阵分解方法,例如潜在语义分析(Latent semantic analysis,LSA)。
- 局部上下文窗口方法,例如 Mikolov 等人提出的 skip-gram 模型。
但是,这两类方法都有明显的缺陷。虽然向 LSA 这样的方法有效地利用了统计信息,但他们在单词类比任务上表现相对较差,这表明不是最优的向量空间结构。像 skip-gram 这样的方法可能在类比任务上做得更好,但是他们很少利用语料库的统计数据,因为它们在单独的局部上下文窗口上训练,而不是在全局共现计数上训练。
2 GloVe 模型
GloVe 的全称叫 Global Vectors for Word Representation,它是一个基于全局词频统计(count-based & overall statistics)的词表征(word representation)工具。
GloVe 的实现主要分为三步:(1)构建共现矩阵;(2)词向量和共现矩阵的近似关系;(3)构造损失函数。
2.1 构建共现矩阵
假设我们有一个语料库,包含以下三个句子:
i like deep learning
i like NLP
i enjoy flying
这个语料库涉及 7 个词:i,like,enjoy,deep,learning,NLP,flying。
假设我们采用一个大小为 3(左右长度为 1)的统计窗口,以第一个语句 “i like deep learning” 为例,则会生成以下窗口内容:
| 窗口标号 | 中心词 | 窗口内容 |
|---|---|---|
| 0 | i | i love |
| 1 | love | i love deep |
| 2 | deep | love deep learning |
| 3 | learning | deep learning |
以窗口 1 为例,中心词为 love,上下文词为 i、deep,则更新共现矩阵中的元素:
X l o v e , i + = 1 X l o v e , d e e p + = 1 X_{love, i} \quad += \quad 1 \\ X_{love, deep} \quad += \quad 1 Xlove,i+=1Xlove,deep+=1
使用以上方法,将整个语料库遍历一遍,即可得到共现矩阵 X X X:
| i | like | enjoy | deep | learning | NLP | flying | |
|---|---|---|---|---|---|---|---|
| i | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| like | 2 | 0 | 0 | 1 | 0 | 1 | 0 |
| enjoy | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| deep | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| learning | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| NLP | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| flying | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
其中,第一列表示中心词词,第一行表示上下文词。
2.2 词向量和共现矩阵的近似关系
在开始前,我们先定义一些变量:
- X i j X_{ij} Xij 表示词 j j j 在词 i i i 上下文中出现的次数。
- X i = ∑ k X i k X_i = \sum_k X_{ik} Xi=∑kXik 表示任何词出现在词 i i i 上下文中的次数。
- P i j = P ( j ∣ i ) = X i j / X i P_{ij} = P(j|i) = X_{ij} / X_{i} Pij=P(j∣i)=Xij/Xi 表示词 j j j 出现在词 i i i 上下文中的概率。
我们来看一下论文作者提供的一个表格:

表 1 显示了一个大型语料库的概率及其比率结果,其中取 i = i c e i=ice i=ice 和 j = s t e a m j=steam j=steam。对于与 ice 有关但与 steam 无关的词 k k k,比如 k = s o l i d k=solid k=solid, P i k / P j k P_{ik}/P_{jk} Pik/Pjk 远大于 1。类似地,对于与 steam 有关但与 ice 无关的词 k k k,比如 k = g a s k=gas k=gas,比率远小于 1。对于像 water 或 fashion 这样的词 k k k,要么与 ice 和 steam 都有关,要么与两者都无关,其比率接近 1。与原始概率相比,该比率能够更好地区分相关词(solid 和 gas)和不相关词(water 和 fashion),并且能够更好地区分两个相关词。
上述论证表明,通过概率的比率而不是概率本身去学习词向量是一个更合适的方法。比率 P i k / P j k P_{ik}/P_{jk} Pik/Pjk 取决于三个词 i i i, j j j 和 k k k,最通用的模型采用以下形式:
F ( w i , w j , w ~ k ) = P i k P j k (1) F(w_i, w_j, \tilde w_k) = \frac{P_{ik}}{P_{jk}}\tag{1} F(wi,wj,w~k)=PjkPik(1)
其中, w ∈ R d w \in \mathbb{R}^d w∈Rd 是词向量, w ~ ∈ R d \tilde{w} \in \mathbb{R}^d w~∈Rd 是单独的上下文词向量。在这个等式中,右边是从语料库中提取的, F F F 可能取决于一些尚未确定的参数。因为向量空间是线性结构的,所以要表达出两个概率的比例差,最自然的方法是使用向量差,即可得到:
F ( w i − w j , w ~ k ) = P i k P j k (2) F(w_i - w_j, \tilde{w}_k) = \frac{P_{ik}}{P_{jk}} \tag{2} F(wi−wj,w~k)=PjkPik(2)
接下来,我们注意到等式(2)中 F F F 的参数是向量,而右边是标量,于是我们把 F F F 的参数作点积操作,得到:
F ( ( w i − w j ) T w ~ k ) = P i k P j k (3) F((w_i - w_j)^T \tilde{w}_k) = \frac{P_{ik}}{P_{jk}} \tag{3} F((wi−wj)Tw~k)=PjkPik(3)
我们知道 X X X 是对称矩阵,词和上下文词其实是相对的,也就是如果我们做如下交换: w ↔ w ~ w \leftrightarrow \tilde{w} w↔w~, X ↔ X T X \leftrightarrow X^T X↔XT,式(3)应该保持不变。很显然,现在的公式是不满足的。然而,对称性可以通过两步实现。首先,我们要求 F F F 满足同态特性,即:
F ( ( w i − w j ) T w ~ k ) = F ( w i T w ~ k ) F ( w j T w ~ k ) (4) F((w_i - w_j)^T \tilde{w}_k) = \frac{F(w_i^T \tilde{w}_k)}{F(w_j^T \tilde{w}_k)} \tag{4} F((wi−wj)Tw~k)=F(wjTw~k)F(wiTw~k)(4)
结合等式(3)得到:
F ( w i T w ~ k ) = P i k = X i k X i (5) F(w_i^T \tilde{w}_k) = P_{ik} = \frac{X_{ik}}{X_i} \tag{5} F(wiTw~k)=Pik=XiXik(5)
令等式(4)中 F = exp F=\exp F=exp,得到:
w i T w ~ k = log ( P i k ) = log ( X i k ) − log ( X i ) (6) w_i^T \tilde{w}_k = \log(P_{ik}) = \log(X_{ik}) - \log(X_i) \tag{6} wiTw~k=log(Pik)=log(Xik)−log(Xi)(6)
接下来,我们注意到,如果不是右边的 log ( X i ) \log(X_i) log(Xi),等式(6)将表现出交换对称性。然而,该项与 k k k 无关,因此它可以被吸收为 w i w_i wi 的偏置项 b i b_i bi。最后,为 w ~ k \tilde{w}_k w~k 添加一个偏置 b ~ k \tilde{b}_k b~k 实现对称性:
w i T w ~ k + b i + b ~ k = log ( X i k ) (7) w_i^T \tilde{w}_k + b_i + \tilde{b}_k = \log(X_{ik}) \tag{7} wiTw~k+bi+b~k=log(Xik)(7)
这样,我们就得到了词向量和共现矩阵之间的近似关系。
2.3 构造损失函数
作者在论文中提出了一个新的加权最小二乘回归模型来构造损失函数。将等式(7)看作一个最小二乘问题,并在损失函数中引入权重函数 f ( X i j ) f(X_{ij}) f(Xij):
J = ∑ i , j = 1 V f ( X i j ) ( w i T w ~ j + b i + b ~ j − log X i j ) 2 (8) J = \sum_{i,j=1}^{V} f(X_{ij})(w_i^T \tilde{w}_j + b_i + \tilde{b}_j - \log X_{ij})^2 \tag{8} J=i,j=1∑Vf(Xij)(wiTw~j+bi+b~j−logXij)2(8)
其中 V V V 是词库的大小。
因为少见的共现携带有噪声,并且比频繁的共现携带更少的信息。添加权重函数可以避免对所有共现事件赋予相同的权重。从而权重函数应符合以下特性:
-
f ( 0 ) = 0 f(0) = 0 f(0)=0。如果 f f f 被看作一个连续函数,它应该随着 x → 0 x \rightarrow 0 x→0 足够快地消失,使得 lim x → 0 f ( x ) log 2 x \lim_{x \rightarrow 0} f(x) \log^2x limx→0f(x)log2x 是有限的。
-
f ( x ) f(x) f(x) 应该是非递减的,这样少见的共现权重不会过大。
-
对于较大的 x x x 值, f ( x ) f(x) f(x) 应该相对较小,这样频繁的共现权重不会过大。
很多函数满足这些性质,作者发现如下形式的函数表现良好:
f ( x ) = { ( x / x m a x ) α , i f ( x < x m a x ) 1 , o t h e r w i s e (9) f(x) = \left \{ \begin{array}{cc} (x/x_{max})^{\alpha}, \quad \mathbb{if}(x < x_{max}) \\ 1, \quad \mathbb{otherwise} \end{array} \right. \tag{9} f(x)={(x/xmax)α,if(x<xmax)1,otherwise(9)
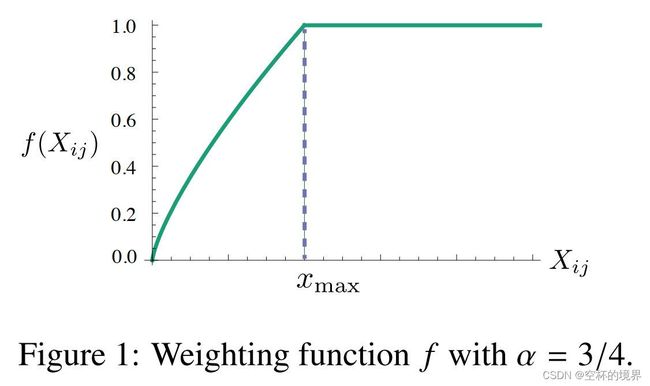
作者在所有实验中将 x m a x x_{max} xmax 固定为 100。并且发现 α = 3 / 4 \alpha=3/4 α=3/4 比 α = 1 \alpha=1 α=1 的线性版本有一定的改进。
3 总结
GloVe 是一个新的全局对数双线性回归模型,用于词向量的无监督学习。它结合了全局矩阵分解和局部上下文窗口方法两者的优点。GloVe 模型通过只训练词-词共现矩阵中的非零元素,而不是整个稀疏矩阵或大型语料库中的单个上下文窗口,有效地利用了统计信息。GloVe 模型生成了一个具有有意义子结构的向量空间。
3.1 GloVe 与 LSA 的区别
LSA 是一种比较早的基于统计的词向量表征工具,它也是基于共现矩阵的,不过其采用基于奇异值分解(SVD)的矩阵分解技术对大矩阵进行降维,因为 SVD 的复杂度很高,所以它的计算代价比较大。还有一点是它对词的统计权重是一致的。这些缺点在 GloVe 中被克服了。
3.2 GloVe 与 word2vec 的区别
Glove 与 word2vec 主要存在以下区别:
- word2vec 使用神经网络根据上下文预测中心词(CBOW)或者根据中心词预测上下文(skip-gram);GloVe 是一个对数双线性回归模型,本质上是对共现矩阵进行降维。
- 都使用了滑窗,不过 word2vec 是直接用来训练,而 GloVe 是为了构建共现矩阵。
- word2vec 只关注了局部信息,GloVe 利用局部信息和全局信息。
- 相比 word2vec,GloVe 的训练速度更快。
参考
[1] GloVe: Global Vectors for Word Representation
[2] 斯坦福大学的词向量工具:GloVe
[3] (十五)通俗易懂理解——Glove算法原理
[4] GloVe 主页