【强化学习Q-Learning算法学习笔记】概念整理+实例+代码解释+ppt

强化学习知识点整理，学习了莫烦python教程中的内容，并写了自己的理解，原链接在下方，非常感谢原作者分享，我整理的ppt全部内容放在文末。

代码来源：https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/blob/master/contents/1_command_line_reinforcement_learning/treasure_on_right.py
参考：https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/1-1-B-RL-methods/
https://www.cnblogs.com/LHWorldBlog/p/9249011.html

目录
1强化学习介绍
1.1强化学习的定义
1.2 强化学习实现的原理
1.3 强化学习的分类
1.4 强化学习的应用场景
2实例讲解Q-Learning算法
1.1应用场景描述
1.2解决思路
1.3计算与推导过程
3一个Q-Learning算法的程序实现
3.1 应用场景描述
3.2 解决思路
3.3 程序讲解与源码
3.4 运行结果展示与分析

（一）强化学习介绍
一、强化学习的定义
什么是强化学习？
以训练狗狗为例：
（1）狗狗在出门时乱跑，给1根肉骨头；
（2）狗狗在出门时跟紧主人，给5根肉骨头；
（3）狗狗试图咬人，不给肉骨头；
（4）狗狗表现非常温顺，给10根肉骨头。
经过这样的训练后，狗狗会怎么做呢？狗狗更可能不会在出门时乱跑，而是跟紧主人，不咬人并表现温顺。
二、强化学习实现的原理

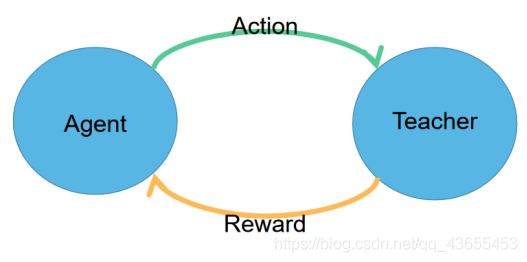
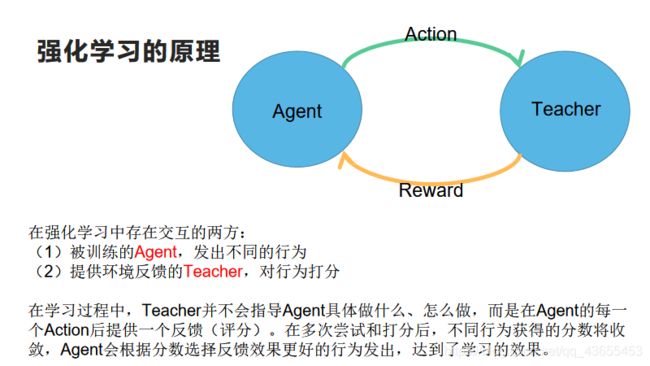
在强化学习中存在交互的两方：
（1）被训练的Agent，发出不同的行为
（2）提供环境反馈的Teacher，对行为打分
在学习过程中，Teacher并不会指导Agent具体做什么、怎么做，而是在Agent的每一个Action后提供一个反馈（评分）。在多次尝试和打分后，不同行为获得的分数将收敛，Agent会根据分数选择反馈效果更好的行为发出，达到了学习的效果。
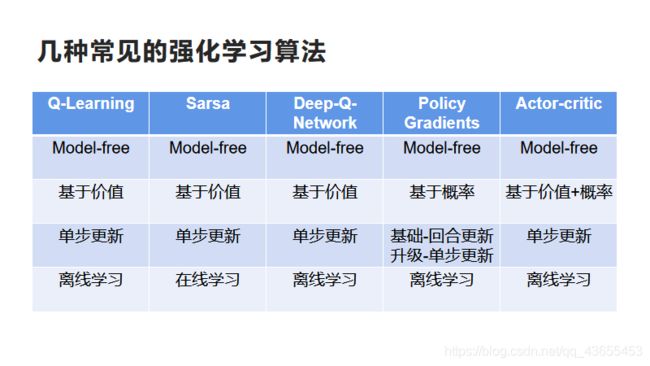
三、强化学习的分类
1.Model-free和Model-based
（1）Model-free:
不理解环境, 环境给什么就是什么。在所做的决定直接作用于实际作出的动作，想什么做什么，不会在做之前进行预想和模拟。
（2）Model-based:
理解环境，并学会用一个模型来代表环境。
相当于在Model-free的基础上，想象出一个虚拟环境，并在这个环境中进行训练的预演。
2.基于概率和基于价值
（1）基于概率：
分析所处的环境, 输出下一步要采取的各种动作的概率，然后根据概率采取行动。每种动作都有可能被选中, 只是可能性不同。即使某个动作的概率最高, 但是还是不一定会选到他。可以用来处理连续值。
（3）基于价值：
分析所处环境，输出所有动作的价值, 选择价值最高的动作。

只能用于处理离散值。
3.回合更新和单步更新
（1）回合更新：
事后复盘。一个回合开始后, 我们要等待本回合结束, 再总结这一回合中的所有转折点，并更新行为准则。
（2）单步更新：
边做边学。伴随着游戏的进行，每一步都更新, 不用等待一个回合的结束, 时刻更新行为准则。
4.在线学习和离线学习
（1）在线学习：
仿佛自己的现实人生，只能活在当下。
需要本人在场本人操作, 并且一定是本人边尝试动作边学习。仅局限在自己的当下一条时间线。
（2）离线学习：
仿佛游戏中的虚拟人生，可以随时切换身份或者跑路重来。
可以选择自己玩, 也可以选择看着别人玩，可以读档拥有其他身份的过往经验并中学习。可以不必边做边学，而是把尝试的结果保存下来，等到想学的时候再进行读档，学习自己当时的记忆。
多身份多时间可读档，多条时间线。
四、强化学习的应用场景
适用于：提供环境标量化反馈，但不提供行为方法的场景。
如：电动游戏、棋类游戏…甚至能超过人类水平。如AlphaGo大战李世石。进一步的，强化学习还可用于解释有限理性条件下的平衡态，设计推荐系统和机器人交互系统。

（二）实例讲解Q-Learning算法
一、应用场景描述
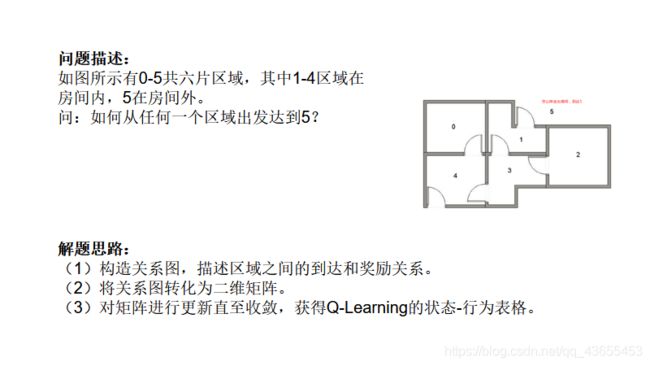
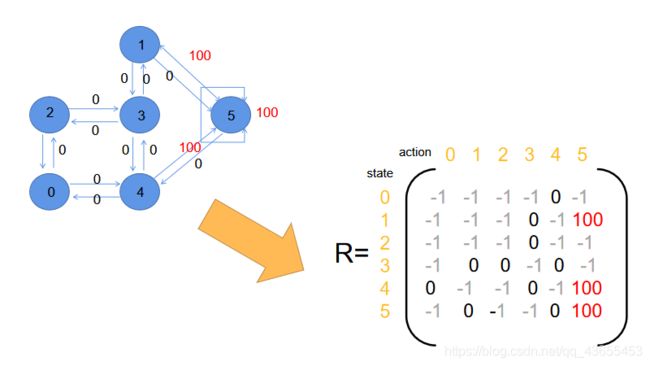
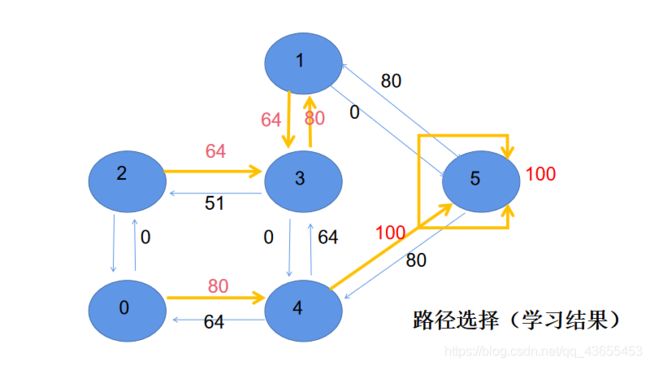
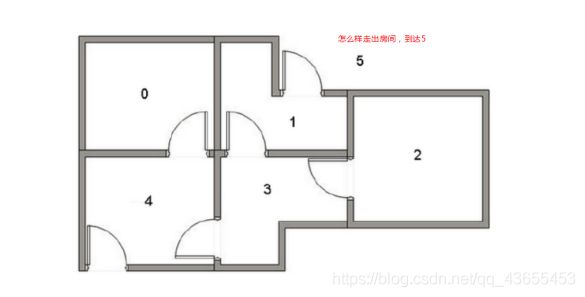
如图所示有0-5共六片区域，其中1-4区域在房间内，5在房间外。
问：如何从任何一个区域出发达到5？

二、解决思路
（1）构造关系图，描述区域之间的到达和奖励关系。
（2）将关系图转化为二维矩阵。
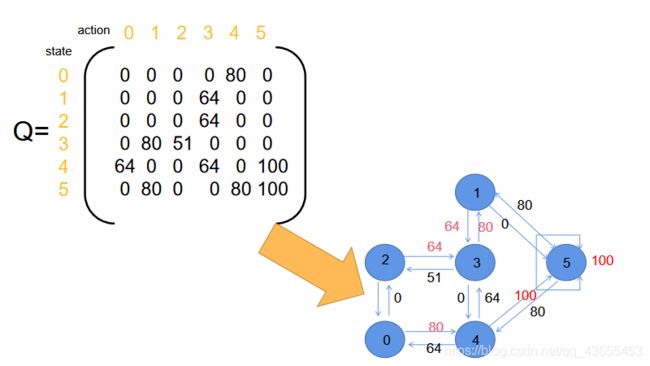
（3）对矩阵进行更新直至收敛，获得Q-Learning的状态-行为表格。
三、计算与推导过程
1.背景知识：
（1）马尔可夫决策
<1> 能够检测到理想的状态
<2> 允许多次尝试
<3> 系统的下个状态至于当前状态信息有关，而与更早之前的状态无关。在决策过程中海域当前采取的措施有关。
（2）符号集说明
S: states状态集
A: actions动作集
P: 状态转移概率
R: reward function 奖励函数
γ：折扣系数，位于[0,1)之间，表示模型的远见程度，γ越小，意味着当下的reward越比未来的重要
（3）Bellman方程

2.构造关系图并转为矩阵
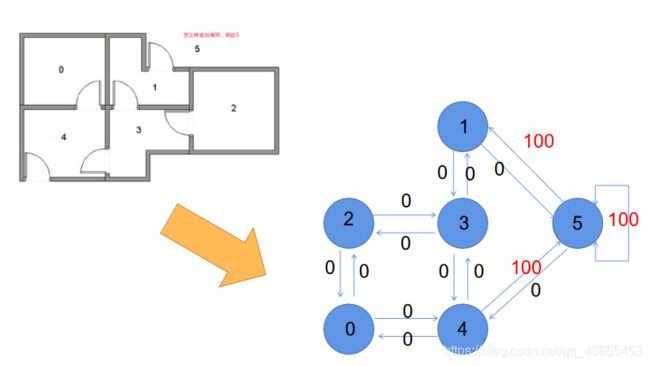
将奖励作为图的权：
（1）能够到达5的，权值为100；
（2）不能到达5的，权值为0。
P.S.在图中，可直达的区域编号用边相连，不可直达的区域编号不会连接；
在矩阵中，可直达的区域编号在对应位置上填值，不可直达的区域编号对应位置上的值置为-1


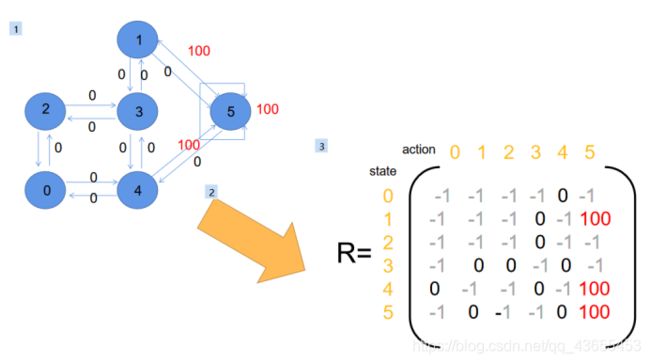
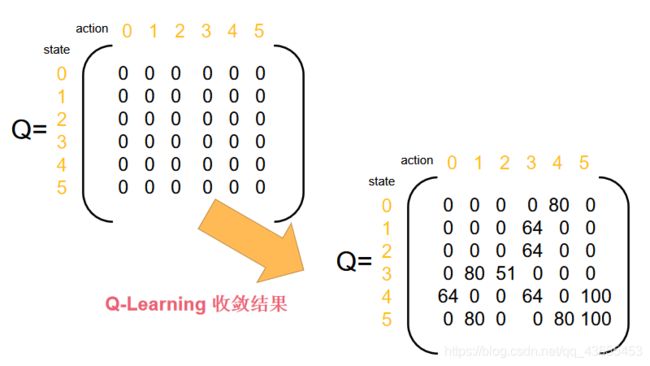
3.执行Q-Learning算法
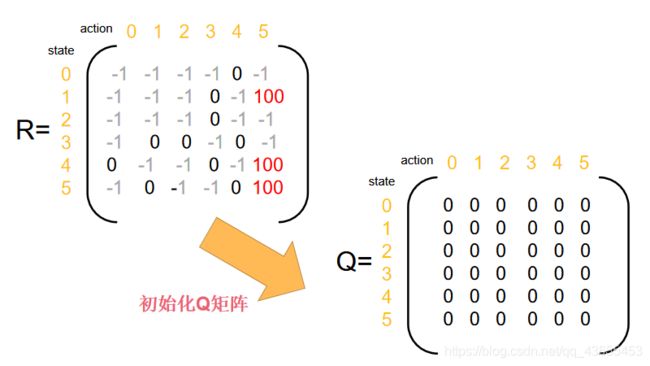
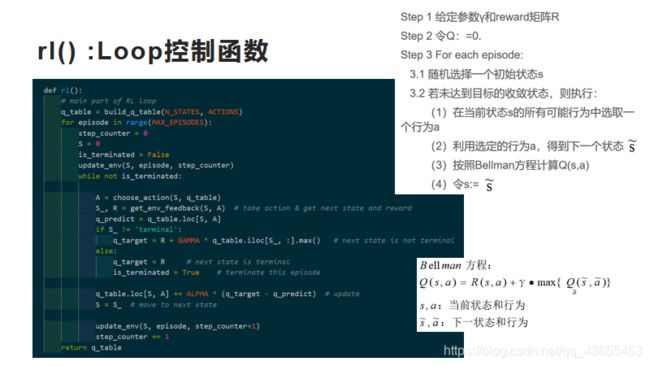
Step 1 给定参数γ和reward矩阵R
Step 2 令Q：=0.
Step 3 For each episode:
3.1 随机选择一个初始状态s
3.2 若未达到目标的收敛状态，则执行：
（1）在当前状态s的所有可能行为中选取一个行为a
（2）利用选定的行为a，得到下一个状态
（3）按照Bellman方程计算Q(s,a)
（4）令s:=s~

（三）一个Q-Learning算法的程序实现
一、应用场景描述
小人找宝藏

在一维空间内，有一个小人o寻找宝藏T，每次他可以选择向右（+1）或向左（-1）移动一步（在不超出两端边界范围的情况下）。宝藏的位置在一维空间的最右处。
求：小人找到宝藏的最快走法。
代码来源：https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/blob/master/contents/1_command_line_reinforcement_learning/treasure_on_right.py
二、解决思路
构造class q_table描述状态-奖励表格（State-Action二维矩阵，矩阵的每个位置存储reward），并定义函数进行矩阵操作，以实现Q-learning算法，并找到最优的状态转移表格q_table。
类内四个函数：
def build_q_table(n_states, actions) #初始化Q-table为零矩阵
def choose_action(state, q_table) #选择下一行为，采取随机的策略
def get_env_feedback(S, A) #左右移动，获得环境反馈
def update_env(S, episode, step_counter) #更新并显示一维世界的当前状态
三、程序讲解与源码
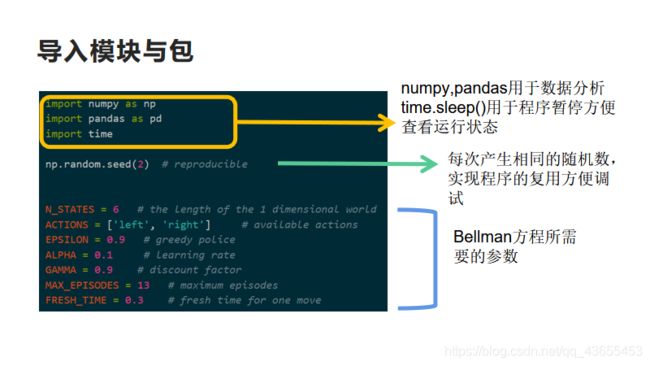
1.导入模块与包

import numpy as np
import pandas as pd
import time

np.random.seed(2)  # reproducible
N_STATES = 6   # the length of the 1 dimensional world
ACTIONS = ['left', 'right']     # available actions
EPSILON = 0.9   # greedy police
ALPHA = 0.1     # learning rate
GAMMA = 0.9    # discount factor
MAX_EPISODES = 13   # maximum episodes
FRESH_TIME = 0.3    # fresh time for one move

numpy,pandas用于数据分析
time.sleep()用于程序暂停方便查看运行状态
np.random.seed(2)每次产生相同的随机数，实现程序的复用方便调试
2.函数：build_q_table(n_states, actions)
初始化Q表：状态(states)数*行为(actions)数的二维零矩阵，列名为状态名。返回初始化完成的空Q表

def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),     # q_table initial values
        columns=actions,    # actions's name
    )
    # print(table)    # show table
    return table

3.函数：choose_action(state, q_table)
给定当前状态state，确定行标.
在state行内采用随机数，任选接下来的action(即随机取列号)。函数返回下一动作

def choose_action(state, q_table):
    # This is how to choose an action
    state_actions = q_table.iloc[state, :]
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):  # act non-greedy or state-action have no value
        action_name = np.random.choice(ACTIONS)
    else:   # act greedy
        action_name = state_actions.idxmax()    # replace argmax to idxmax as argmax means a different function in newer version of pandas
    return action_name

4.函数：get_env_feedback(S, A)
向右移动：
若达到宝藏位置（一维世界的最右位置），则位置不再右移，反馈评分为1；
否则右移位置+1，反馈评分为0.
向左移动：
若达到一维世界的左边界，则位置不再左移，反馈评分为0；
否则左移位置-1，反馈评分为0.

def get_env_feedback(S, A):
    # This is how agent will interact with the environment
    if A == 'right':    # move right
        if S == N_STATES - 2:   # terminate
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:   # move left
        R = 0
        if S == 0:
            S_ = S  # reach the wall
        else:
            S_ = S - 1
    return S_, R
5.函数：update_env(S, episode, step_counter)
若到达宝藏位置，则打印本回合的序号和经历的步数。
否则打印本次移动后小人的位置（一维世界的当前状态）
def update_env(S, episode, step_counter):
    # This is how environment be updated
    env_list = ['-']*(N_STATES-1) + ['T']   # '---------T' our environment
    if S == 'terminal':
        interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                                ', end='')
    else:
        env_list[S] = 'o'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)

5.rl() :Loop控制函数

def rl():
    # main part of RL loop
    q_table = build_q_table(N_STATES, ACTIONS)
    for episode in range(MAX_EPISODES):
        step_counter = 0
        S = 0
        is_terminated = False
        update_env(S, episode, step_counter)
        while not is_terminated:
            A = choose_action(S, q_table)
            S_, R = get_env_feedback(S, A)  # take action & get next state and reward
            q_predict = q_table.loc[S, A]
            if S_ != 'terminal':
                q_target = R + GAMMA * q_table.iloc[S_, :].max()   # next state is not terminal
            else:
                q_target = R     # next state is terminal
                is_terminated = True    # terminate this episode
            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  # update
            S = S_  # move to next state
            update_env(S, episode, step_counter+1)
            step_counter += 1
    return q_table
if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

四、运行结果展示与分析

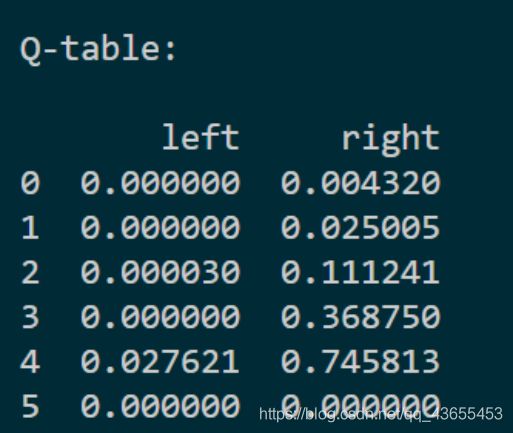
Q表分析：
right>left，向右的reward大于向左。
在0,1,2,3,4位置，小人均向右移动，以达到接近宝藏的效果。5位置为terminal，故不移动时最接近宝藏。
left=right=0

全部ppt内容：