（九）特征提取之主成分分析（PCA）

主成分分析（PCA）

一、PCA算法是如何实现的？

简单来说，就是将数据从原始的空间中转换到新的特征空间中，例如原始的空间是三维的(x,y,z)，x、y、z分别是原始空间的三个基，我们可以通过某种方法，用新的坐标系(a,b,c)来表示原始的数据，那么a、b、c就是新的基，它们组成新的特征空间。在新的特征空间中，可能所有的数据在c上的投影都接近于0，即可以忽略，那么我们就可以直接用(a,b)来表示数据，这样数据就从三维的(x,y,z)降到了二维的(a,b)。
所谓的在某个轴投影接近于0的理解如下图，数据在x轴的投影在0附近，我们可以舍去x轴，只用数据在y轴的投影来表示数据。

二、如何求新的基(a,b,c)

一般步骤是这样的：

1. 对原始数据零均值化（中心化），
2. 求协方差矩阵，
3. 对协方差矩阵求特征向量和特征值，这些特征向量组成了新的特征空间。

1、PCA–零均值化（中心化）

中心化即是指变量减去它的均值，使均值为0。
其实就是一个平移的过程，平移后使得所有数据的中心点是(0,0)

只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。
此图形象的表述了，中心化的几何意义，就是将样本集的中心平移到坐标系的原点O上。

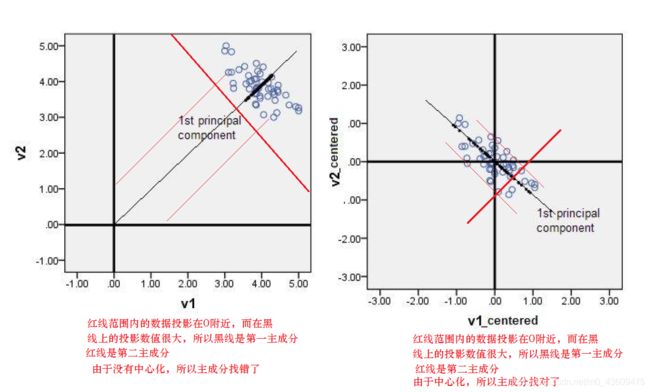
2、PCA–PCA降维的几何意义：

我们对于一组数据，如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据。所以在进行降维的时候，主要目的是找到一个超平面，它能使得数据点的分布方差呈最大，这样数据表现在新的坐标轴上时候已经足够分散了。

方差（Variance）：是度量一组数据分散的程度。方差是各个样本与样本均值的差的平方和的均值

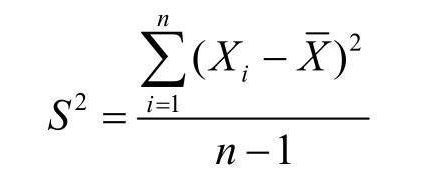
3、PCA算法的优化目标:

① 降维后同一维度的方差最大
② 不同维度之间的相关性为0

4、通俗理解PCA

PCA可以将高维数据集映射到低维空间的同时，尽可能的保留更多变量。PCA旋转数据集与其主成分对齐，将最多的变量保留到第一主成分中。假设我们有下图所示的数据集：
数据集看起来像一个从原点到右上角延伸的细长扁平的椭圆。要降低整个数据集的维度，我们必须把点映射成一条线。下图中的两条线都是数据集可以映射的，映射到哪条线样本变化最大？
显然，样本映射到黑色虚线的变化比映射到红色点线的变化要大的多。实际上，这条黑色虚线就是第一主成分。第二主成分必须与第一主成分正交，也就是说第二主成分必须是在统计学上独立的，会出现在与第一主成分垂直的方向，如下图所示：
后面的每个主成分也会尽量多的保留剩下的变量，唯一的要求就是每一个主成分需要和前面的主成分正交。
现在假设数据集是三维的，散点图看起来像是沿着一个轴旋转的圆盘。
这些点可以通过旋转和变换使圆盘完全变成二维的。现在这些点看着像一个椭圆，第三维上基本没有变量，可以被忽略。
当数据集不同维度上的方差分布不均匀的时候，PCA最有用。（如果是一个球壳行数据集，PCA不能有效的发挥作用，因为各个方向上的方差都相等；没有丢失大量的信息维度一个都不能忽略）。

5、PCA–协方差

协方差就是一种用来度量两个随机变量关系的统计量。

协方差（Covariance）： 是度量两个变量的变动的同步程度，也就是度量两个变量线性相关性程度。同一元素的协方差就表示该元素的方差，不同元素之间的协方差就表示它们的相关性。如果两个变量的协方差为0，则统计学上认为二者线性无关。注意两个无关的变量并非完全独立，只是没有线性相关性而已。计算公式如下：

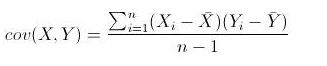
当Y为X是则变成了求X的方差：

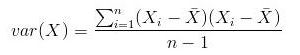
协方差的性质：
有方差和协方差定义可以看出

协方差的意义：

6、PCA–协方差矩阵

对n个变量求协方差时得到的是一个协方差矩阵：

例如，比如，三维变量(x,y,z)的协方差矩阵：

协方差矩阵的特点：
• 协方差矩阵计算的是不同维度之间的协方差， 而不是不同样本之间的。
• 样本矩阵的每行是一个样本， 每列为一个维度， 所以我们要按列计算均值。
• 协方差矩阵的对角线就是各个维度上的方差
• 协方差矩阵是对称矩阵

特别的，如果变量做了中心化，则协方差矩阵为（中心化矩阵的协方差矩阵公式）：

计算协方差矩阵时，要保证，行数和列数都是变量个数
例如：假设我们只有a和b两个变量，其已经中心化了，那么我们将它们按行组成矩阵X：

然后我们用X乘以X的转置，并乘上系数1/m：

因此根据这个结果可以有：
设我们有m个n维数据记录，将其按列排成n（变量数）乘m（变量数据个数）的矩阵X，设，则C是一个对称矩阵，其对角线分别个各个变量的方差，而第i行j列和j行i列元素相同，表示i和j两个变量的协方差。

7、PCA–求特征值、特征矩阵

特征值与特征向量的定义：
A为n阶矩阵，若数λ和n维非0列向量x满足Ax=λx，那么数λ称为A的特征值，x称为A的对应于特征值λ
的特征向量。

式Ax=λx也可写成( A-λE)x=0，并且|λE-A|叫做A 的特征多项式。当特征多项式等于0的时候，称为A的特征方程，特征方程是一个齐次线性方程组，求解特征值的过程其实就是求解特征方程的解。

对于协方差矩阵A，其特征值（ 可能有多个）计算方法为：

求解矩阵的特征值和特征向量举例：
nmpy计算特征值特征向量

8、计算原数据的主成分

将特征值按照从大到小的排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵W(nxk)
*计算XnewW，即将数据集Xnew投影到选取的特征向量上，这样就得到了我们需要的已经降维的数据集XneuW。

三、总结

根据上面对PCA的数学原理的解释，我们可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。
因此，PCA也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关，关于这点就不展开讨论了。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就大打折扣了。
最后需要说明的是，PCA是一种无参数技术，也就是说面对同样的数据，如果不考虑清洗，谁来做结果都一样，没有主观参数的介入，所以PCA便于通用实现，但是本身无法个性化的优化.
参考

四、实现

import numpy as np

X = np.array([[10, 15, 29],
              [15, 46, 13],
              [23, 21, 30],
              [11, 9,  35],
              [42, 45, 11],
              [9,  48, 5],
              [11, 21, 14],
              [8,  5,  15],
              [11, 12, 21],
              [21, 20, 25]])
class PCA:
    def __init__(self,X,K):
        self.X = X
        self.K = K
    def Centralized(self):
        '''
        样本中心化，样本值减去均值
        :return:
        '''
        # 求平均值
        mean = np.mean(self.X, axis=0)  # axis=0，计算每一列的均值
        # 中心化
        Center_X = self.X-mean
        print("中心化：\n",Center_X)
        return Center_X
    def Covariance(self):
        '''求中心化后数据的协方差'''
        Center_X = self.Centralized()
        m = Center_X.shape[0]
        Cov_Array = np.dot(Center_X.T,Center_X)*(1/(m-1))
        print("协方差矩阵：\n",Cov_Array)
        return Cov_Array
    def Eigenvalues_and_eigenvectors(self,X):
        '''求特征值与特征向量'''
        eigenvalue, eigenvectors = np.linalg.eig(X)
        print("特征值：\n",eigenvalue)
        print("特征向量：\n",eigenvectors)
        return eigenvalue,eigenvectors
    def Calculation_PCA(self):
        '''计算PCA'''

        # 获取协方差矩阵
        Cov_Array = self.Covariance()
        # 获取协方差矩阵的特征值和特征向量矩阵（列对应的是特特征向量）
        eigenvalue, eigenvectors = self.Eigenvalues_and_eigenvectors(Cov_Array)
        # 获取特征值从大到小排序下标
        # eigenvalue_sort = eigenvalue.argsort()[::-1]
        eigenvalue_sort = np.argsort(-1*eigenvalue)
        # 取前K个特征向量
        eigenvectors_Top_K = []
        for i in range(self.K):
            eigenvectors_Top_K.append(eigenvectors[:,eigenvalue_sort[i]].tolist())
        eigenvectors_Top_K = np.transpose(np.array(eigenvectors_Top_K))
        print("特征值排序：\n",eigenvalue_sort)
        print("特征值排序前K个特征值对应的特征向量：\n",eigenvectors_Top_K)
        # 用原始数据 点乘 前K个特征向量
        PCA_X = np.dot(self.X,eigenvectors_Top_K)
        print("PCA结果：\n",PCA_X)

pca = PCA(X,2)
# pca.Centralized()
# Cov_Array = pca.Covariance()
# pca.Eigenvalues_and_eigenvectors(Cov_Array)
pca.Calculation_PCA()