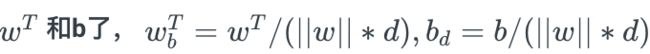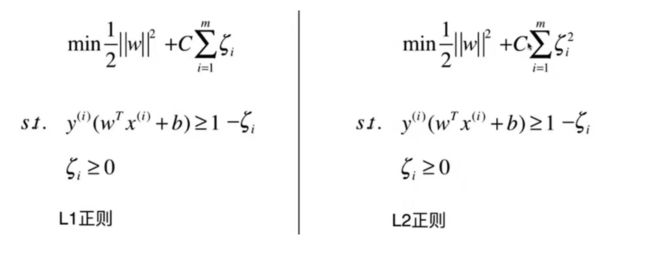机器学习----支撑向量机(SVM)

SVM

支持向量机（Support Vector Machine, SVM）

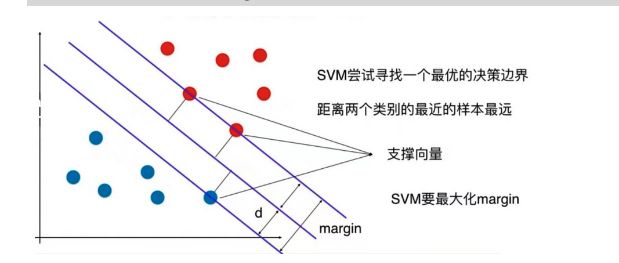
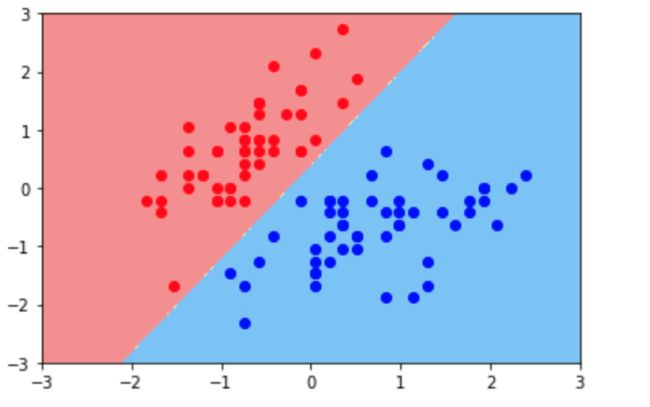
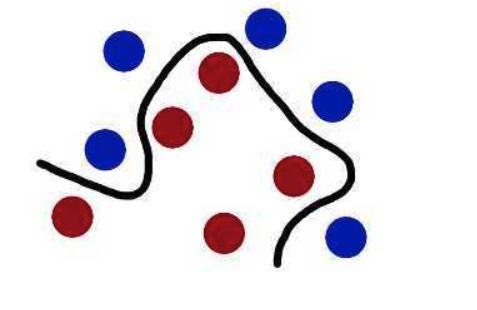
图中是一个样本空间，里面有一些样本点，分成红色和蓝色两类。
逻辑回归是要找到一根决策边界，由决策边界把数据分成两类。但可能存在这样一些数据（下图），可能存在多条决策边界。（不适定问题）

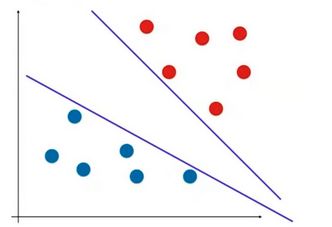
逻辑回归定义了一个损失函数，通过最小化损失函数求出决策边界。
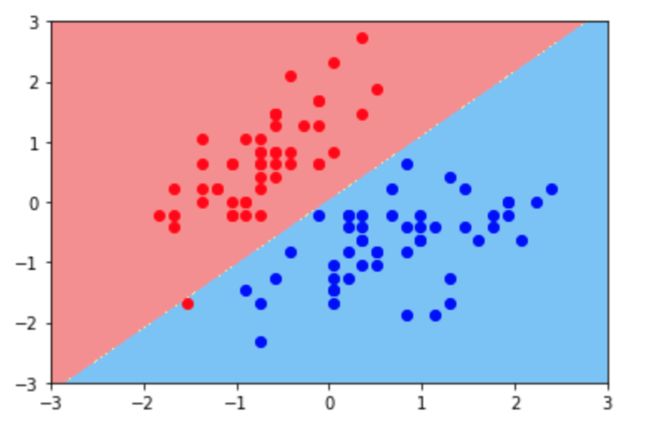
假设逻辑回归算法最后求出的是这样一根直线（下图），它在前面的所给的样本空间中表现很好，但新来这样一个样本，那么很有可能它的分类结果是错误的。

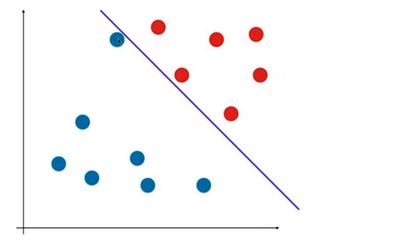
这根决策边界的泛化效果不够好，因为它离红色样本点太近了。那么怎样的决策边界泛化能力比较好呢？
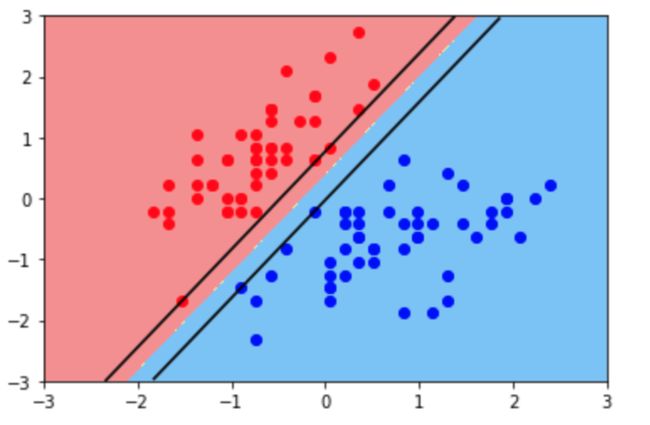
看上去下图这根直线的泛化能力要更好一点。

离这根直线最近的点有3个，让这3个点离这根直线的距离尽可能地远。
也就是说，让这个决策边界既离红线尽可能远，也离蓝点尽可能远。于是得到了上图这样的决策边界。
它不仅将训练数据划分开类，还期望它的泛化能力尽可能好。它把对泛化能力的考量直接放到了算法的内部。
把以上的思考用数学方式表达出来就是，让离决策边界最近的三个点，到决策边界的距离应该是一样的并且尽可能地大。
基于这三个点又找两根与决策边界平行的直线。这两根直线定义了一个区域。这个区域中不再有任何点。

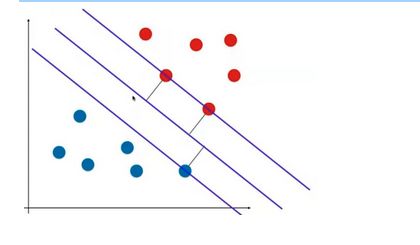
SVM要最大化margin，即图中两根直线之间的距离

用数学语言来表达: margin = 2 * d，最大化d就是最大化margin

推广: 点x到直线 wT∗x+b=0 的距离为

所有的样本点到决策边界到距离都应该大于d，用于公式表达：
这里需要注意, SVM的二分类问题target是 1, - 1 而不是 0, 1 ps -1 具有神奇作用

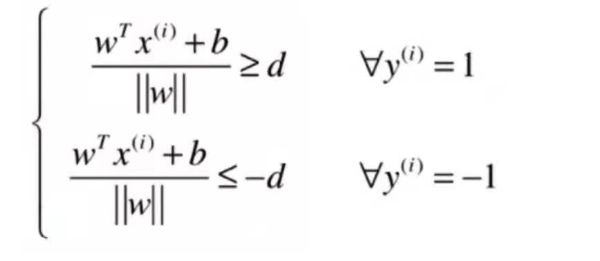
于是可得出margin上下两条直线的方程为：

注意：上图的三条直线中的已经不是原来的

SVM的目标是最大化d，d的公式在上文已经给出。
由于支持向量x一定是在margin的上下边界点上，可以证明对于任意支持向量x，以下四个公式表达的目标的相同的：

结论： SVM算法演变为有条件的最优化问题，（st：条件）推到过程不做介绍


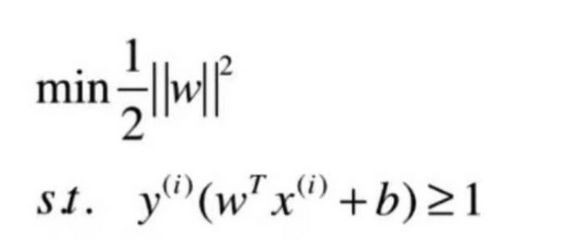
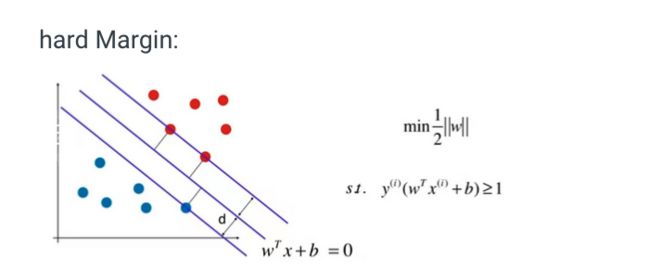
使用这种方法，对下面这张图中的样本，hard SVM会给出这样一根决策边界

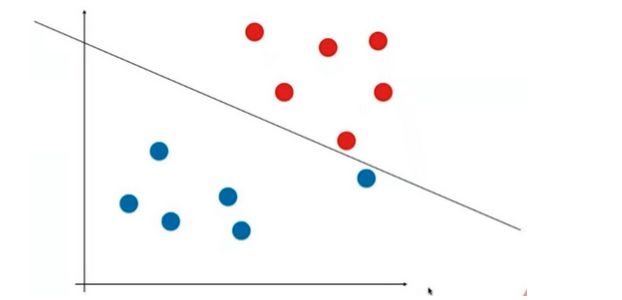
hard SVM非常明显地受到一个蓝点的影响，而这个蓝点很有可能是outlier或者是个错误点。

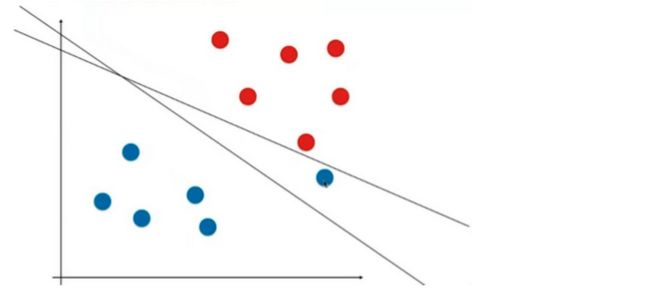
而对于下图这样的样本点，线性不可分的情况，hard SVN是无解的。

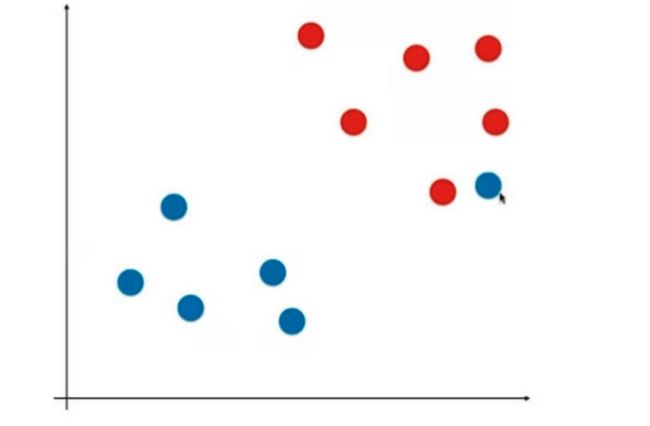
Hard SVM需要更好的容错性(允许犯适当的错误)。
改进：增加一个宽松量
也就是 Soft SVM

即允许一些点出现在图中虚线和实线之间的位置。
这里的宽松量不是一个定值，它对每一个样本都是不同的。
同时还要最小化所有的宽松量。
目标函数变成了：

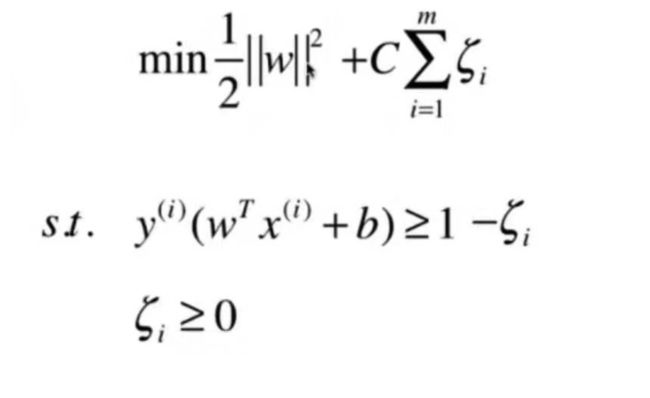
L1正则、L2正则

和KNN一样，使用SVM之前要做数据标准化处理，因为SVM算法涉及距离。
尺度不平衡的例子

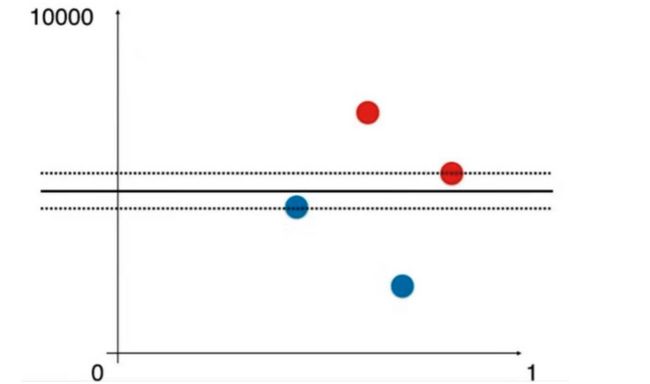
数据标准化之后：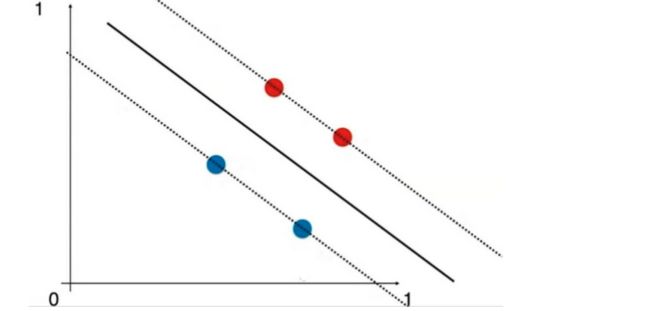

Sklearn中的SVM

• 准备数据并且进行标准化

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)
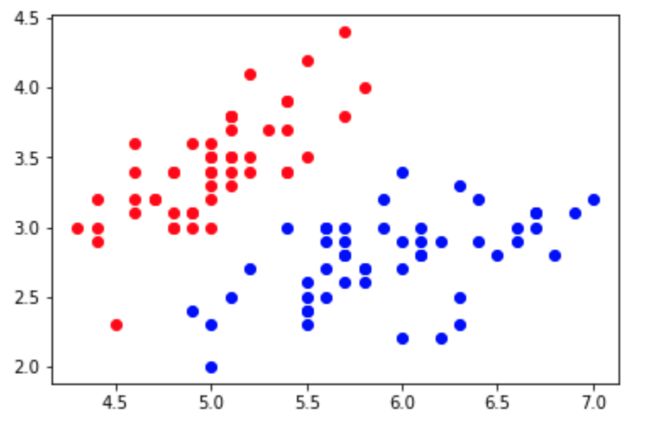
plt.scatter(X[y==0,0], X[y==0,1], color='red')
plt.scatter(X[y==1,0], X[y==1,1], color='blue')
plt.show()

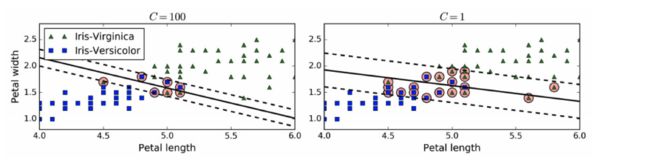
训练Hard SVM

from sklearn.svm import LinearSVC # Support Vector Classifier
svc = LinearSVC(C=1e9) # C越大, 越hard
svc.fit(X_standard, y)
def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),)
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, cmap=custom_c
                 map)
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
## 需要标准化之后的
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color='blue')
plt.show()

训练Soft SVM

svc2 = LinearSVC(C=0.01) # C越大, 越hard
svc2.fit(X_standard, y)
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
## 需要标准化之后的
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color='blue')
plt.show()
# 图中有一个点被错误地分类了，这是soft的效果

绘制margin

输入：svc.coef_
输出：array([[ 4.03240038, -2.50701084]])
样本中有两个特征，所以有2个系数，每个特征对应一个
输出是一个二维数组，因为sklearn提供的SVM算法可以处理多分类问题

输入：svc.intercept_
输出：array([0.92736326])

# 修改绘制函数
def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),)
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
    # 增加margin的那两根直线
    w = model.coef_[0]
    b = model.intercept_[0]
    # w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1  纵轴
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y =  -w[0]/w[1] * plot_x - b/w[1]  + 1/w[1] 
    down_y =  -w[0]/w[1] * plot_x - b/w[1]  - 1/w[1] 
    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])
    plt.plot(plot_x[up_index], up_y[up_index], color='black')
    plt.plot(plot_x[down_index], down_y[down_index], color='black')
# hard svm margin 两个直线里面没有样本
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color='blue')
plt.show()  

# soft svm margin
plot_svc_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color='blue')
plt.show() 

• scikit-learn提供的SVM算法支持多分类，默认使用ovr算法
• scikit-learn提供的SVM算法支持正则化，默认使用L2范数

SVM中使用多项式特征

进行非线性分割

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
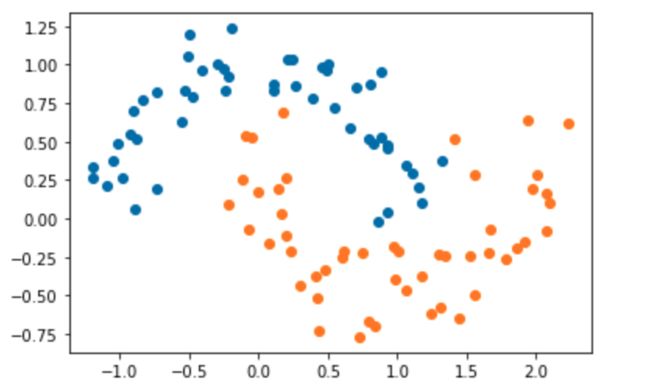
X, y = datasets.make_moons(noise=0.15,random_state=666)
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree, C=1.0):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("linearSVC", LinearSVC(C=C)),
    ])

使用三阶多项式

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree, C=1.0):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("linearSVC", LinearSVC(C=C)),
    ])

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),)
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
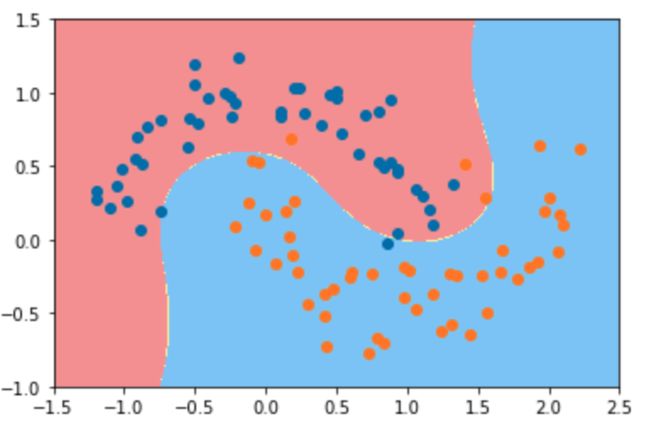
poly_svc3 = PolynomialSVC(degree=3)
poly_svc3.fit(X, y)
plot_decision_boundary(poly_svc3,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

直接使用SVC中的多项式核函数

不需要创建多项式特征

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def PolynomialKernelSVC(degree, C=1.0):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("kernelSVC", SVC(C=C, kernel='poly', degree=degree)),
    ])
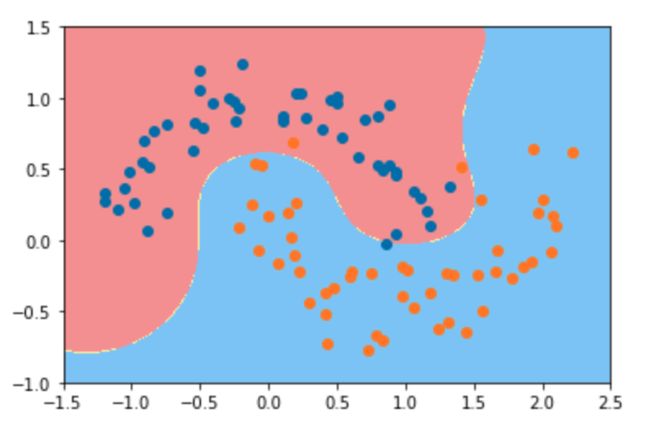
poly_kernel_svc3 = PolynomialSVC(degree=3)
poly_kernel_svc3.fit(X, y)
plot_decision_boundary(poly_kernel_svc3,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

使用RBF和函数

K(x, y)表示x和y的点乘。高斯核函数的公式为：
公式中的 $\gamma$ 是高斯核函数中唯一的超参数。
高斯核函数 = RBF核 = Radial Basis Function Kernel = 镜像基函数
高斯核函数本质是将每个样本点映射到一个无穷维的特征空间

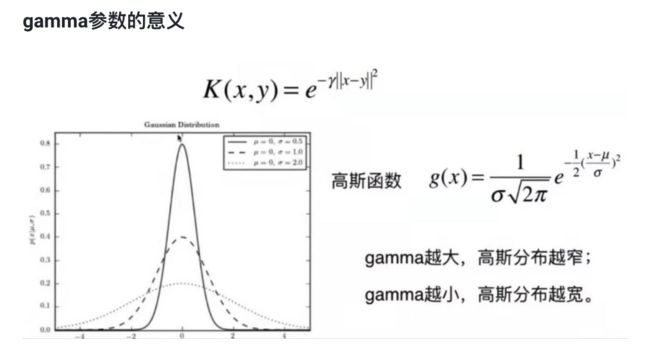
感知RBF中的 $\gamma$ 大小对分类的影响

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma =1.0):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("rbfSVC", SVC(kernel='rbf', gamma=gamma)),
    ])
rbf_svc = RBFKernelSVC()
print(rbf_svc.fit(X, y))
plot_decision_boundary(rbf_svc,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

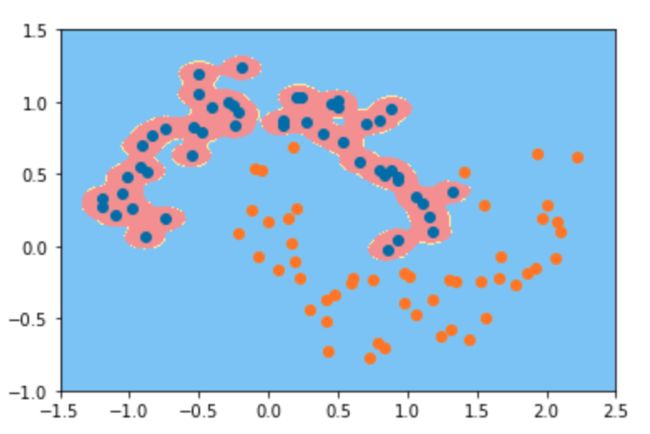
rbf_svc = RBFKernelSVC(gamma=100)
print(rbf_svc.fit(X, y))
plot_decision_boundary(rbf_svc,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
# 可以俯视的看做每一个点是一个高斯分布, 此时gamma越大代表模型越复杂

rbf_svc = RBFKernelSVC(gamma=10)
print(rbf_svc.fit(X, y))
plot_decision_boundary(rbf_svc,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
# 可以俯视的看做每一个点是一个高斯分布, 此时gamma越大代表模型越复杂

rbf_svc = RBFKernelSVC(gamma=0.1)
print(rbf_svc.fit(X, y))
plot_decision_boundary(rbf_svc,axis=[-1.5, 2.5, -1, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
# 可以俯视的看做每一个点是一个高斯分布, 此时gamma越大代表模型越复杂

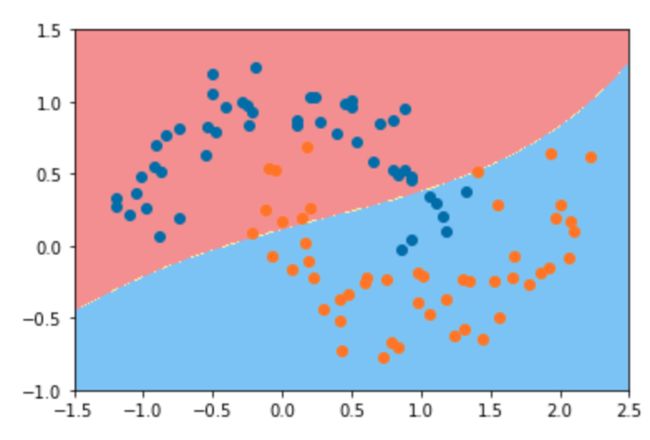
可以把训练的效果看成是俯视这些样本点。某一类的每个样本点形成了一个以它为中心的正态分布。gamma越大，这个分布的圈就越小

SVM 解决回归问题

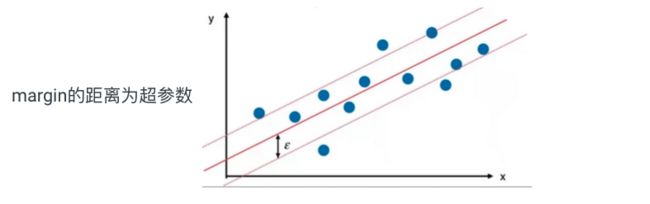
回归问题是指找到一根直线/曲线最大程度的拟合样本点。不同的回归算法对“拟合”有不同的理解。
例如线性回归算法定义“拟合”为：所有样本点到直线的MSE最小, 而SVM将“拟合”定义为：尽可能多的点被包含在margin范围内，取margin中间的直线。（与解决分类问题相反的思路）

• 加载数据

import numpy as np
from sklearn import datasets

boston = datasets.load_boston()
x = boston.data
y = boston.target

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=666)

• 训练

# 训练
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.svm import LinearSVR
from sklearn.pipeline import Pipeline
def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("linearSVR", LinearSVR(epsilon=epsilon)),
    ])
svr = StandardLinearSVR()
svr.fit(X_train, y_train)
svr.score(X_test, y_test)

0.635614183982528

练习

每日必会题

1 选择题

1. 下列关于SVM的应用场景说法正确的是（多选）：（ABCD）

A. SVM在二分类问题上表现突出

B. SVM能够解决多分类问题

C. SVM能够解决回归问题

D. SVM能够完成异常值检测

2. 下列关于SVM的硬间隔和软间隔说法错误的是：（B）

A. 硬间隔在线性可分的样本中表现才会好

B. 硬间隔对异常值不是很敏感

C. 软间隔在线性不可分样本中的表现更好

D. 软间隔需要在限制间隔违例和模型复杂度之间进行权衡

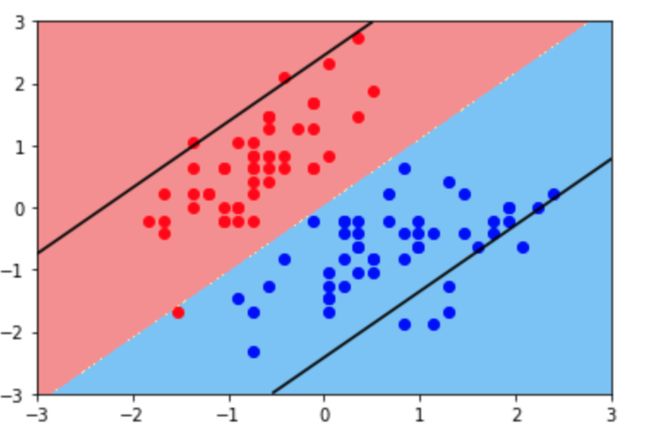
3. 给出如下图中的样本数据，想要对它们进行分类，能够使用的机器学习算法是(多选)：（AD）

A. logistics回归

B. 线性回归

C. 朴素贝叶斯

D. SVM

4. 下图中使用SVM软间隔分别对样本数据进行划分，哪个图中的划分方式可能获得较好的模型泛化能力：（B）
   

A. 左图

B. 右图

C. 都不行

D. 都可以

5. 下面关于SVM算法原理的说法错误的是：（D）

A. SVM通过计算样本到分割超平面的最大距离来确定最优模型

B. 在样本线性不可分的情况下引入核函数是一个明智的选择

C. 分割超平面的法向量可用于计算样本与分割超平面之间的最短距离

D. 最大化间隔就是最大化$$||w|{|}^2$$，其中 $$w$$ 是分割超平面的权重系数

6. 关于SVM的目标函数求解，下列说法错误的是：（C）

A. 目标函数往往带有多个约束条件，我们无法直接快速求解

B. 使用拉格朗日乘子法能解决多约束条件下的目标函数求极值问题

C. 使用拉格朗日乘子法得到的最小最大值问题即为最终的优化问题

D. 对偶问题能够将最小最大值问题转换为最大最小值问题

7. 关于SVM的损失函数，下列说法中错误的是：（D）

A. SVM适用于多种损失函数

B. 0/1损失函数的最终结果只有两个，0代表分类正确，1代表分类错误

C. 合页损失衡量了被误分类的样本离分割超平面的距离的大小程度

D. 分类SVM常用平方误差损失来衡量模型的好坏

8. 关于SVM核函数，下列说法中错误的是：（C）

A. 核函数的引入极大的提升了SVM在线性不可分场景下的模型的稳健性

B. 核函数就是一类具有将某一类输入映射为某一类输出的函数

C. 核函数把特征映射到的空间维度越高越好

D. 常见的核函数有线性核、高斯核、多项式核、sigmoid核

2 简答题

一、简述SVM算法在线性可分样本上的二分类实现原理。

答：

假设这里我们有 $$m$$ 个线性可分的样本 $$(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m)$$ ，

其中 $$x$$ 为 $$n$$ 为特征向量。 $$y$$ 为二元输出，值为 $$1$$ ，或者 $$-1$$ 。

我们最终要确定的是 $$SVM$$ 分割超平面的参数 $$w^{\ast }$$ 和 $$b^{\ast }$$ 以及分类决策函数。

算法的实现过程如下：

① 通过拉格朗日乘子法构造目标函数：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^n{\alpha }_i(y_i(w^T\cdot \Phi (x_i)+b)-1)$$
② 对上述目标函数分别对 $$w$$ 和 $$b$$ 求偏导，令偏导数等于零，求解出此时的 $$w$$ 和 $$b$$ ：
$$\frac{\partial L(w,b,\alpha )}{\partial w}=0\Rightarrow w=\sum _{i=1}^n{\alpha }_i{y}_i\Phi (x_n)$$

$$\frac{\partial L(w,b,\alpha )}{\partial b}=0\Rightarrow \sum _{i=1}^n{\alpha }_i{y}_i=0$$

③ 将求得的上述结果回代到第①步的目标函数中得到如下结果：
$$L(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T(x_i)\Phi (x_j)$$
④ 根据对偶问题将求解上述目标函数的极大值，转化为求解下式的极小值：
$$L^{\prime }(\alpha )=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T(x_i)\Phi (x_j)-\sum _{i=1}^m{\alpha }_i$$
⑤ 根据 $$KKT$$ 条件构造约束问题：
$$min\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^m{\alpha }_i$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\cdots ,m$$

⑥ 求解在满足上述约束条件下的 $$L^{\prime }(\alpha )$$ 的极值，只需要对 $$\alpha$$ 求导并求出驻点即可，

假设此时求出的使目标函数取得最小值的 $$\alpha$$ 向量的值为 $${\alpha }^{\ast }$$ 。

⑦ 根据求解出的 $$\alpha$$ 向量以及样本数据，再根据第②步中求得的解析式，

我们很快就能计算出此时分割超平面的权重 $$w^{\ast }$$ 和偏置 $$b_s^{\ast }$$ ：
$$w^{\ast }=\sum _{i=1}^n{\alpha }_i^{\ast }{y}_i{x}_i$$

$$b_s^{\ast }=y_s-\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i(x_i\cdot x_s)$$

⑧ 最终的偏置 $$b^{\ast }$$ 即为根据所有符合条件的支撑向量求出的 $$b_s^{\ast }$$ 的和的平均值：
$$b^{\ast }=\frac{1}{S}\sum _{i=1}^S{b}_s^{\ast }$$
⑨ 最终的分类决策函数为：
$$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$

二、请简述在线性不可分样本中SVM引入核函数的目的，常见的核函数以及它们的使用场景和效果。

答：
① 我们遇到线性不可分的样例时，常用做法是把样本特征映射到高维空间中去。
但是遇到线性不可分的样本，一律映射到高维空间，那么这个维度大小是会高到令人恐怖的。
此时，核函数就体现出它的价值了，核函数的价值在于它虽然也是将特征进行从低维到高维的转换，
但核函数好在它在低维上进行计算，而将实质上的分类效果（利用了内积）表现在了高维上，
这样避免了直接在高维空间中的复杂计算，真正解决了SVM线性不可分的问题。

② 事实上，核函数的研究非常的早，要比SVM出现早得多，当然，
将它引入SVM中是最近二十多年的事情。对于从低维到高维的映射，核函数不止一个。

而自己去找一个核函数是很难的，怎么办呢？还好前人已经帮我们找到了很多的核函数，而常用的核函数也仅仅只有那么几个。

1. **线性核函数（Linear Kernel）**适用于线性可分的样本集上，分类效果良好：
   $$K(x,z)=x\cdot z$$

2. **多项式核函数（Polynomial Kernel）**是线性不可分SVM常用的核函数之一，
   但是由于其需要调节的超参数过多，需要耗费较大的人力和物力，一般少有人会选择去使用它：
   $$K(x,z)=(\gamma x\cdot z+r{)}^d$$
   其中， $$\gamma ,r,d$$ 都需要自己调参定义。

3）高斯核函数（Gaussian Kernel），在SVM中也称为径向基核函数（Radial Basis Function,RBF），
它是非线性分类SVM最主流的核函数，它的效率相比于多项式核函数要更加出众：
$$K(x,z)=e^{(-\gamma ||x-z|{|}^2)}$$
其中， $$\gamma$$ 大于0，需要自己调参定义。

4）**Sigmoid核函数（Sigmoid Kernel）**也是线性不可分SVM常用的核函数之一，

在某些线性不可分样本集中表现也不错：
$$K(x,z)=tanh(\gamma x\cdot z+r)$$
其中， $$\gamma ,r$$ 都需要自己调参定义。

企业面试题

1. 一个SVM模型存在欠拟合问题，下面怎么做能提高模型的性能：（A）

A. 增大惩罚参数C

B. 减小惩罚参数C

C. 减小核函数系数（gamma值）

答案解析：

C >0称为惩罚参数，C值大时对误差分类的惩罚增大，当C越大，趋近无穷的时候，表示不允许分类误差的存在，margin越小，容易过拟合。

C值小时对误差分类的惩罚减小,当C趋于0时，表示我们不再关注分类是否正确，只要求margin越大，容易欠拟合。

2. 下列有关SVM说法不正确的是：（C）

A. SVM使用核函数的过程实质是进行特征转换的过程

B. SVM对线性不可分的数据有较好的分类性能

C. SVM因为使用了核函数，因此它没有过拟合的风险

D. SVM的支持向量是少数的几个数据点向量

答案解析：

正是因为有了核函数，低维线性不可分的数据映射到高维空间，更容易线性可分，极端情况下某些噪音点也可以线性可分正确，所以才更有可能出现过拟合。

3. 关于logistic回归和SVM的说法不正确的是：（A）

A. Logistic回归目标函数是最小化后验概率

B. Logistic回归可以用于预测事件发生概率的大小

C. SVM可以实现结构风险最小化

D. SVM可以有效避免模型过拟合

答案解析：

二分类逻辑回归的模型为：
$$P(Y=1|x)=\frac{e^{w\cdot x}}{1+e^{w\cdot x}}$$

$$P(Y=0|x)=\frac{1}{1+e^{w\cdot x}}$$

其中：$$w=(w^1,w^2,\cdots ,w^n,b{)}^T$$ ， $$x=(x^1,x^2,\cdots ,x^n,1{)}^T$$ 。

它的目标函数是对数似然函数：
$$L(w)=ln(\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i})$$
其中： $$\pi (x)=P(Y=1|x)$$ ； $$x_i\in R^n$$ ， $$y_i\in \{0,1\}$$ 。

这里是要求解参数 $$w$$ 的值让 $$L(w)$$ 取得最大值，对 $$L(w)$$ 进行化简可得：
$$L(w)=y_i\pi (x_i)+(1-y_i)[1-\pi (x_i){]}^{}$$
不管是 $$y_i=0$$ 还是 $$y_i=1$$ 的情况，都是要求得 $$\pi (x_i)$$ 的极大值，才能让 $$L(w)$$ 取得极大值，所以A是错误的，应该是最大化后验概率。

关于什么是先验概率、后验概率：

P(θ) 是在没有数据支持下，θ 发生的概率：先验概率

P(θ|x) 是在数据X的支持下，θ 发生的概率：后验概率

p(x|θ) 是给定参数 θ 的概率分布：似然函数

logit回归输出的是Y属于某一类的概率，也可以表示某事件发生的概率，B正确。

SVM通过寻找使得训练数据尽可能分开且分类间隔最大的超平面实现结构风险最小化，C正确。

SVM通过减小惩罚参数C来避免过拟合，因为C越大，分类就越苛刻，越容易过拟合，D正确。

4. 有两个样本点，第一个点为正样本，它的特征向量是（0, -1）；第二个点为负样本，它的特征向量是（2, 3），从这两个样本点组成的训练集构建一个线性SVM分类器的分类面方程是：（C）

A. 2x + y = 4

B. x + 2y = 5

C. x + 2y = 3

D. 2x - y = 0

答案解析：

这道题简化了样本数据和样本的维度，但是基于线性可分的样本使用SVM进行分类的大致原理都是相同的。
对于两个点来说，最大间隔就是两点连线的垂直平分线，因此求出垂直平分线即可。两点连线的垂直平分线的斜率是两点连线的斜率的负倒数-1/((-1-3)/(0-2)) = -1/2, 可得y=-(1/2)x + c, 过中点((0+2)/2, (-1+3)/2) = (1, 1), 可得c=3/2, 故答案选C.

2

1. 使用分类SVM完成对数字识别器的练习。

要求：

1. 使用train.csv中的数据作为训练数据，test.csv中的数据作为测试集数据；
2. 使用训练集数据找到合适的模型；
3. 构造合适的方法查看样本图片；
4. 使用合适的特征预处理方法处理特征数据；
5. 使用合适的方法对特征数据进行降维处理；
6. 尝试调节API中的超参数，然后对比调节之后的模型，并与同学进行讨论。

代码示例：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.preprocessing import StandardScaler
import time
from sklearn.decomposition import PCA

train = pd.read_csv("./data/mnist/train.csv")
test = pd.read_csv("./data/mnist/test.csv")

# 获取特征值和目标值
train_image = train.iloc[:, 1:]
train_label = train.iloc[:, 0]


# 定义通过图片特征查看图片真实面貌的函数
def image_show(data, n):
    image = data.iloc[n,].values.reshape(28, 28)
    plt.imshow(image)
    plt.axis("off")
    plt.show()

# 查看样本中的其中一张图片
# image_show(train_image, 10)

# 对特征数据进行标准化处理
ss = StandardScaler()
train_data = ss.fit_transform(train_image)

# 对测试集进行划分
x_train, x_val, y_train, y_val = train_test_split(train_data, train_label, test_size=0.2, random_state=6)


# 寻找最优的PCA降维参数
def n_components_analysis(n, x_train, x_val, y_train, y_val):
    # 记录开始时间
    start = time.time()

    # pca降维
    pca = PCA(n_components=n)
    pca.fit(x_train)

    # 在训练集和测试集进行降维
    x_train_pca = pca.transform(x_train)
    x_val_pca = pca.transform(x_val)

    # 利用svc进行训练
    ss = svm.SVC()
    ss.fit(x_train_pca, y_train)

    # 获取accuracy结果
    accuracy = ss.score(x_val_pca, y_val)

    # 记录结束时间
    end = time.time()
    print("n_components={}时，准确率是:{}, 降维和训练共耗时:{}s".format(n, accuracy, int(end - start)))

    return accuracy

# 提供多个n_components参数进行筛选
n_cps = list(np.linspace(0.70, 0.90, num=5))
accuracy = []
for n in n_cps:
    acc = n_components_analysis(n, x_train, x_val, y_train, y_val)
    accuracy.append(acc)

# 将准确率可视化展示
plt.plot(n_cps, np.array(accuracy), "r")
plt.show()

# 根据图像可知当n_components=0.75时模型效果比较好

# 使用测试集进行预测
# 先对数据进行标准化
test_data = ss.transform(test)
# 降维
pca = PCA(n_components=0.75)
pca.fit(x_train)
x_train_pca = pca.transform(x_train)
test_data_pca = pca.transform(test_data)


# 因为test.csv中的数据不包含label，所以我们从中随机获取30个样本进行手动标注label
def save_figure(data, num):
    step = 168
    end = step * (num-1) + 1
    index = list(np.arange(0, end, step))
    for i, n in enumerate(index):
        image = data.iloc[n,].values.reshape(28, 28)
        plt.imshow(image)
        plt.axis("off")
        plt.savefig("./data/mnist/test_label/{}.png".format(i))

    return index

# 获取手动标注样本的索引和真实图片
index = save_figure(test, 30)

# 构建测试数据集label(通过保存的图片查看)
test_label = np.array([2, 3, 0, 1, 4, 1, 3, 2, 3, 4, 3, 5, 0, 6, 9, 0, 8, 4, 2, 8, 3, 7, 2, 4, 7, 3, 7, 7, 0, 4])

# 构建模型，调整参数并训练、预测
param_c = [1, 10, 100]
for c in param_c:
    svc = svm.SVC(C=c)
    svc.fit(x_train_pca, y_train)
    pre = svc.predict(test_data_pca)
    # 获取我们随机抽取的那30个样本的预测值
    pre = pre[index]
    # 计算准确率
    acc = np.mean(test_label == pre)
    print("当正则化系数C={}时，模型准确率为：{}".format(c, acc))

2. 拓展阅读

https://scikit-learn.org/stable/modules/classes.html?highlight=sklearn svm#module-sklearn.svm