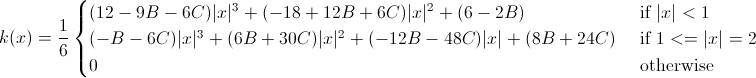Applying Sampling Theory To Real-Time Graphics
原文地址:https://mynameismjp.wordpress.com/2012/10/21/applying-sampling-theory-to-real-time-graphics/
Applying Sampling Theory To Real-Time Graphics
计算机图形学是一个不断地处理离散采样和信号重建的领域,虽然你可能并不会主要到它。这篇文章会聚焦在采样理论被应用到图形和3D渲染上的常规的执行任务处。
Image Scaling
图像缩放
The concepts of sampling theory can are most easily applicable to graphics in the form of image scaling. An image, or bitmap, is typically the result of sampling a color signal at discrete XY sample points (pixels) that are evenly distributed on a 2D grid. To rescale it to a different number of pixels, we need to calculate a new color value at sample points that are different from the original pixel locations. In the previous article we mentioned that this process is known as resampling, and is also referred to as interpolation. Any graphics programmer should be familiar with the point (also known as nearest-neighbor) and linear(also known as bilinear) interpolation modes supported natively in GPU’s which are used when sampling textures. In case you’re not familiar, point filtering simply picks the closest texel to the sample point and uses that value. Bilinear filtering on the other hand picks the 4 closest texels, and linearly interpolates those values in the X and Y directions based on the location of the sample point relative to the texels. It turns out that these modes are both just implementations of a reconstruction filter, with point interpolation using a box function and linear interpolation using a triangle function. If you look back at the diagrams showing reconstruction with a box function and triangle function, you can actually see how the reconstructed signal resembles the visual result that you get when performing point and linear sampling. With the box function you end up getting a reconstructed value that’s “snapped” to the nearest original sample point, while with a triangle function you end up with straight lines connecting the sample points. If you’ve used point and linear filtering, you probably also intuitively understand that point filtering inherently results in more aliasing than linear filtering when resizing an image. For reference, here’s an image showing the same rotated checkerboard pattern being resampled with a box filter and a triangle filter:
采样理论的概念能够很容易地以图像缩放的形式应用到图形中。一个图像或者位图通常是对一个颜色信号在离散的XY方向上的采样结果,这些采样点是均匀地分布在一个2D的网格中。为了能够缩放到不同数量的像素(K:采样点),我们需要在与之前的采样点不同的采样位置上计算新的颜色值。在之前的文章中我们提到这个过程被称为resampling(K:重采样),也被称作为interpolation(K:插值)。任何的图形程序员都会熟悉点(被认为是最近的)和线性(被认为是双线性的)插值形式,当采样贴图的时候这两种形式是被GPU所原生支持的。防止你对此并不熟悉,点采样会简单地提取距离采样点最近的纹理像素并使用这个值。另一方面,双线性采样提取邻近的4个文理像素,并在这些纹理像素相对应的采样点下,在X和Y的方向上通过双线性插值获得最终的结果。结果是,这些模式都是同过reconstruction filter来实现的,点采样使用box function,线性插值使用triangle function。如果你回顾展示重建的box function和triangle function的图表,你实际上能够看到重建后的信号类似于当你执行点和线性采样的视觉效果。使用box function你获得的重建值会"中断"在最近的原始采样点,而当使用一个triangle function你最终会得到在一条直线上的采样点。如果你使用点和线性滤波,你也可能感性地理解,当缩放一个图像时,比起线性采样,点滤波本身会产生更多的走样。为了提供相应的参考,这里有一个图像显示了相同的已经被旋转过的checkerboard pattern在被box filter和triangle filter重采样后的结果:
Knowing what we do about aliasing and reconstruction filters, we can now put some mathematical foundation behind what we intuitively knew all along. The box function’s frequency domain equivalent (the sinc function) is smoother and wider than the triangle function’s frequency domain equivalent (the sinc2 function), which results in significantly more postaliasing. Of course we should note even though the triangle function might be considered among the the “low end” of reconstruction filters in terms of quality, it is still attractive due to its low performance impact. Not only is the triangle function very cheap to evaluate at a given point in terms of ALU instructions, but more importantly the function evaluates to 0 for all distances greater than or equal to 1. This is important for performance, because it means that any pixels that are further than a distance of 1.0 from the resampled pixel location will not have to be considered. Ultimately this means that we only need to fetch a maximum of 4 pixels (in a 2×2 area) for linear filtering, which limits bandwidth usage and cache misses. For point filtering the situation is even better, since the box function hits zero at 0.5 (it has a width of 1.0) and thus we only need to fetch one pixel.
在理解我们对采样和reconstruction fitlers所做,我们现在可以将我们一直都直观理解到隐藏在背后的数学基础拿出来了。box function在频域中的等价曲线(sinc function)比triangle function在频域的等价曲线(sinc2 函数)要更宽更平滑,这会导致更多的postaliasing。当然我们也应该知道,尽管triangle function可能会让人觉得在质量上是一个"低端"的reconstruction fitlers,但它仍然吸引人的理由是它对性能的影响较少。在一个指定的采样点上,triangle function不止在使用ALU指令上有较低的开销,而且更重要的是这个函数在大于或等于1的距离上计算的结果都是零。在性能上这是重要的,这意味着只要采样的像素位置大于1时都不需要考虑。最终我们只需要提取最大是4个像素的区域(在一个2x2的区域上)来进行线性滤波,这能够限制bandwidth的使用和缓存的丢失。对于点滤波的情况甚至有更好的结果,因为box function只在以0为原点(采样点为原点)、0.5像素为半径的区域寻找,因此我们只需要提取一个像素(K:这里的描述,和上图给出的图像有点不一致,因为这里说的box function宽度只有1(半径为0.5),但上图中现实的box function的宽度是[-1,1]之间,宽度很明显是1的,不知道是作者的错误还是我理解有问题)。
Outside of realtime 3D rendering, it is common to use cubic filters (also known as bicubic filters) as a higher-quality alternative to point and linear filters when scaling images. A cubic filter is not a single filtering function, but rather a family of filters that interpolate using a 3rd-order (cubic) polynomial. The use of such functions in image processing dates back to Hsieh Hou’s paper entitled “Cubic Splines for Image Interpolation and Digital Filtering”[1] which proposed using cubic B-splines as the basis for interpolation. Cubic splines are attractive for filtering because they can be used to create functions where the 1stderivative is continuous across the entire domain range, which known as being C1 continuous. Being C1 continuous also implies that the function is C0 continuous, which means that the 0th derivative is also continuous. So in other words, the function itself will would have no visible discontinuities if you were to plot the function. Remember that there is an inverse relationship between rate of change in the spatial domain and the frequency domain, therefore a smooth function without discontinuities is desirable for reducing postaliasing. A second reason that cubic splines are attractive is that the functions can be made to be zero-valued after a certain point, much like a box or triangle function. This means the filter will have a limited width, which is optimal from a performance point of view. Typically cubic filters use functions defined along the [-2, 2] range, which is double the width of a unit triangle function. Finally, a third reason for the attractiveness of cubic filters is that they can be made to produce acceptable results when applied as a seperable filter. Seperable filters can be applied independently in two passes along the X and Y dimensions, which reduces the number of neighboring pixels that need to be considered when applying the filter and thus improves the performance.
在实时3D渲染之外,当在缩放图像时,使用cubic filters作为相对于点和线性滤波来讲更高质量的候选是很常见的(也被称为bicubic filters)。一个cubic filter 不只是一个单独的滤波函数,更是一类使用三次多项式插值的滤波器。在图像处理中这类函数的使用要追溯到Hsieh Hous's的论文,题目叫做"Cubic Splines for Image Interpolation and Digital Filtering",这篇论文提议使用cubic B-splines作为插值的基础。对于滤波来讲cubic splines是吸引的,因为他们能够被用来创建函数,这些函数的一阶导数在整个作用域都是连续的,这被称作为C1 连续。C1 连续也意味着C0 连续,意思是第0阶到时也是连续的。换句话讲,函数自身将没有任何可以看到的不连续的部分,如果你要绘制这个函数的话。记住,变化率在时域和频域中有相反的关系,因为一个平滑的没有不连续的函数在降低postaliasing是让人期待的。关于cubic splines吸引的第二个原因是,这类函数能够在某个点之后(K:baseband bandwidth的位置),函数值都为0,就如box和triangle function一样。这意味着这类滤波器有有限的宽度,在性能的角度看是最优的。通常,cubic filters定义在[-2,2]的范围内,相对于unit triangle function来讲,是它的两倍。最后,第三个吸引的地方是,cubic filter能够作为separable filter产生出让人能够接受的结果。Separable filters能够单独的通过两个passed应用到X和Y的方向上,当应用这个filter的时候,这能够减少邻近像素需要被考虑到的数量,因为能够体高性能(K:想象一下一个全屏的高斯模糊后处理,就能够使用两个filter分别应用到X和Y方向上)。
In 1988, Don Mitchell and Arun Netravali published a paper entitled Reconstruction Filters in Computer Graphics[2] which narrowed down the set of possible of cubic filtering functions into a generalized form dependent on two parameters called B and C. This family of functions produces filtering functions that are always C1 continuous, and are normalized such that area under the curve is equal to one. The general form they devised is found below:
在1988年,Don Mitchell和Arun Netravali发表了一篇名为"Reconstruction Filters in Computer Graphics"的论文,这篇论文能够将一系列cubic滤波函数,归结为一种只依赖两个参数的通用格式,这两个参数被称为B和C。这一系列的函数产生出滤波函数,这些函数总是C1连续的,并且被归一化致使这个曲线能够在一个区域为1的范围内。他们发现的这个通用的格式如下:
Generalized form for cubic filtering functions
Below you can find graphs of some of the common curves in use by popular image processing software[3], as well as the result of using them to enlarge the rotated checkerboard pattern that we used earlier:
在下面的图标中你能够找到一些通用的曲线,它们被用到一些流行的图像处理软件中,也会被用到我们之前提到的,放大旋转的checkerboard样式的结果中:
Common cubic filtering functions using Mitchell’s generalized form for cubic filtering. From top- left going clockwise: cubic(1, 0) AKA cubic B-spline, cubic(1/3, 1/3) AKA Mitchell filter, cubic(0, 0.75) AKA Photoshop bicubic filter, and cubic(0, 0.5) AKA Catmull-Rom spline
Cubic filters used to enlarge a rotated checkerboard pattern
One critical point touched upon in Mitchell’s paper is that the sinc function isn’t usually desirable for image scaling, since by nature the pixel structure of an image leads to discontinuities which results in unbounded frequencies. Therefore ideal reconstruction isn’t possible, and ringing artifacts will occur due to Gibb’s phenomenon. Ringing was identified by Schrieber and Troxel[4] as being one of four negative artifacts that can occur when using cubic filters, with the other three being aliasing, blurring and anisotropy effects. Blurring is recognized as the loss of detail due to too much attenuation of higher frequencies, and is often caused by a filter kernel that is too wide. Anisotropic effects are artifacts that occur due to applying the function as a separable filter, where the resulting 2D filtering function doesn’t end up being radially symmetrical.
关于Mitchell's论文中的一个重要的观点是,sinc function在图像放大方面并不通常被使用,因为一个图像原生的像素格式会导致到不连续的出现,导致出现unbounded frequencies(K:这个名词不知道怎么翻译)。因此理想的重建是不可能的,并且由于Gibb's现象(K:曲线的Y轴有负数出现),ringing瑕疵也会发生。Ringing被Schrieber和Troxel发现,由于细节的丢失而被认为是一种负面的人为行迹,这种细节丢失的原因是在于太多的高频衰减导致的,这个高频衰减通常是因为filter核心太宽。各向异性的效果是有缺陷的,这种现象发生的原因在于,将一个separable fitler应用到这个函数,而2D滤波函数却并不是径向对称的。
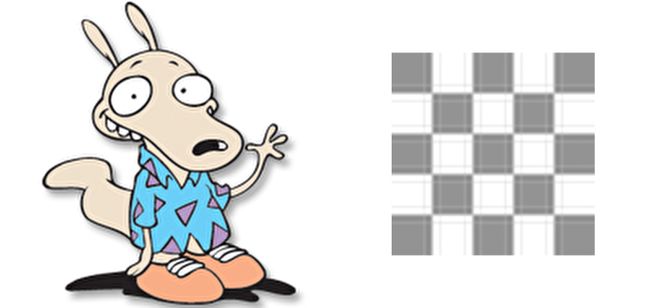
Mitchell suggested that the purely frequency domain-focused techniques of filter design were insufficient for designing a filter that produces subjectively pleasing results to the human eye, and instead emphasized balancing the 4 previously-mentioned artifacts against the amount of postaliasing in order to design a high-quality filter for image scaling. He also suggested studying human perceptual response to certain artifacts in order to subjectively determine how objectionable they may be. For instance, Earl Brown[5] discovered that ringing from a single negative lobe can actually increase perceived sharpness in an image, and thus can be a desirable effect in certain scenarios. He also pointed out that ringing from multiple negative lobes, such as what you get from a sinc function, will always degrade quality. Here’s an image of our friend Rocko enlarged with a Sinc filter, as well as an image of a checkerboard pattern enlarged with the same filter:
Mitchell建议,在设计一个滤波器时,想要让人的眼睛主观上感觉到舒服,紧紧是针对频域的滤波设计技术是不足够的,转而强调平衡前面提到的4种缺陷,能为图像缩放,设计出质量更好的滤波器。他也建议,研究人类的感知反应,在某几个缺陷上是如何主观地决定他们有多难以接受。例如,Earl Brown发现,来自单个负值的波瓣的ringing实际上会增加人类感知图像的锐利程度,因此在某些情况下能够作为被引入的效果。他也指出,来自多个负值的波瓣,例如你通过sinc函数获得的,将总是降低图像质量。下面有两张张使用sinc filter放大的图片,一张是我们的朋友Rocko,一张checkerboard pattern:
Ringing from multiple lobes caused by enlargement with a windowed sinc filter
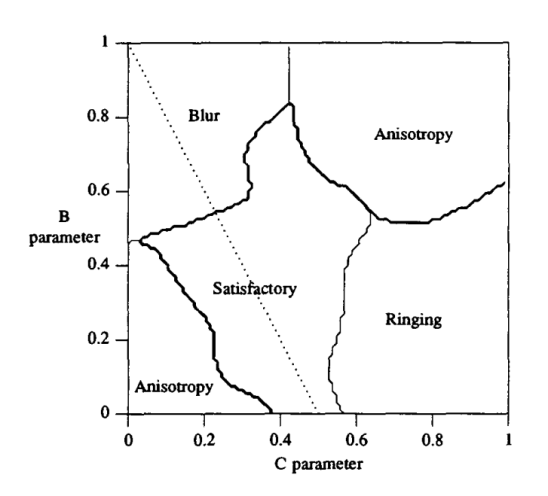
Ultimately, Mitchell segmented the domain of his B and C parameters into what he called “regions of dominant subjective behavior”. In other words, he determined which values of each parameter resulted in undesirable artifacts. In his paper he included the following chart showing which artifacts were associated with certain ranges of the B and C parameters:
最终,Mitchell分离了B和C参数所在的区域,被他称为"占优势的主观行为区域"。换句话讲,他决定每个参数在哪个区域会导致不想要的瑕疵。在他的论文中,他引用了下面的图表,用于展示人工瑕疵是怎样与B和C参数的范围产生联系的:
Based on his analysis, Mitchell determined that (1/3, 1/3) produced the highest-quality results. For that reason, it is common to refer to the resulting function as a “Mitchell filter”. The following images show the results of using non-ideal parameters to enlarge Rocko, as well as the results from using Mitchell’s suggested parameters:
基于他的分析,Mitchell认为(1/3,1/3)能够产生出最高质量的结果。基于这个原因,这个函数通常被称为"Mitchell filter"。下面的图像显示了使用非理想参数和使用Mitchell's建议的参数去放大Rocko:
Undesirable artifacts caused by enlargement using cubic filtering. The top left image demonstrates anisotropy effects, the top right image demonstrates excessive blurring, and the bottom left demonstrates excessive ringing. The bottom right images uses a Mitchell filiter, representing ideal results for a cubic filter. Note that these images have all been enlarged an extra 2x with point filtering after resizing with the cubic filter, so that the artifacts are more easier to see.
使用cubic filtering而引入的不可取的人工瑕疵。左上是anisotropy效果,右上是过度的blurring,左下是过度的ringing,右下是使用Mitchell filiter,显示出了cubic filter的理想效果。需要注意的是,这些图像在经过cubic filter之后,使用point filtering额外放大了两倍,为了能够让人工瑕疵能够更容易的被看到。
Texture Mapping
纹理贴图
Real-time 3D rendering via rasterization brings about its own particular issues related to aliasing, as well as specialized solutions for dealing with them. One such issue is aliasing resulting from resampling textures at runtime in order to map them to a triangle’s 2D projection in screen space, which I’ll refer to as texture aliasing. If we take the case of a 2D texture mapped to a quad that is perfectly perpendicular to the camera, texture sampling essentially boils down to a classic image scaling problem: we have a texture with some width and height, the quad is scaled to cover a grid of screen pixels with a different width and height, and the image must be resampled at the pixel locations where pixel shading occurs. We already mentioned in the previous section that 3D hardware is natively capable of applying “linear” filtering with a triangle function. Such filtering is sufficient for avoiding severe aliasing artifacts when upscaling or downscaling, although for downscaling this only holds true when downscaling by a factor <= 2.0. Linear filtering will also prevent aliasing when rotating an image, which is important in the context of 3D graphics since geometry will often be rotated arbitrarily relative to the camera. Like image scaling, rotation is really just a resampling problem and thus the same principles apply. The following image shows how the pixel shader sampling rate changes for a triangle as it’s scaled and rotated:
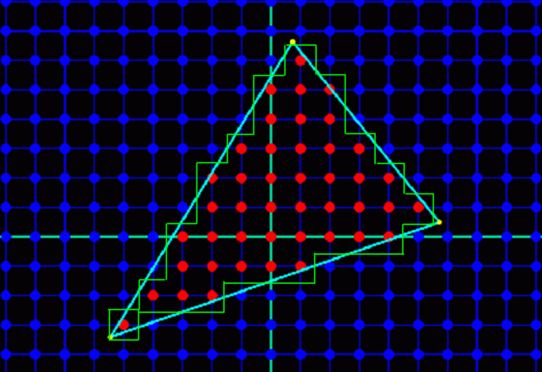
实时3D渲染通过光栅化会引入与走样相关的特定问题,也会有相应的办法可以处理它们。一个问题是,在运行时,将贴图映射到一个经过2D投影后,在屏幕坐标中显示的三角形中,而由于重采样贴图而产生的走样,我将会称作为texture aliasing(纹理走样)。如果我们将一个经过2D纹理映射的四边形完美地垂直于摄像机,纹理采样将会归结为一个传统的图像缩放问题:我们有一个一定大小的贴图,四边形被缩放到覆盖屏幕中的像素网格,该网格的长宽与纹理长宽是不一样的,这导致图像必须重采样到相应的像素位置,该位置就是着色发生的地方。在前面我们已经提到过,3D硬件原生具有"线性"滤波的能力,其使用的是一个triangle function。当我们缩小或放大时,这样的滤波在避免走样瑕疵时是足够的,需要注意的是,在缩小时,当缩小的倍数小于等于2倍的时候,线性滤波才是足够的。线性滤波能够防止经过旋转后的图像发生走样,这是很重要的,因为在3D图形学中,几何体将会由于摄像机的原因,经常被任意旋转。就如图像缩放一样,旋转也只是一个重采样的问题,因此能够应用相应的法则。下面的图像显示了,经过旋转和缩放的三角形,导致的采样率变化后,像素是如何被着色的:
Pixel sampling rates for a triangle. Pixel shaders are executed at a grid of fixed locations in screen space (represented by the red dots in the image), thus the sampling rate for a texture depends on the position, orientation, and projection of a given triangle. The green triangle represents the larger blue triangle after being scaled and rotated, and thus having a lower sampling rate.
一个三角形的像素采样率。像素着色器在屏幕的固定网格位置处被执行(用红色的点标注在图像中),因此,一个贴图的采样率是基于位置,朝向和三角形的投影。蓝色的三角形经过旋转和缩放后形成绿色的三角形,因此具有一个更低的采样率。
Mipmapping
Mipmapping(K:贴图分级细化??总感觉这样的翻译怪怪的)
When downscaling by a factor greater than 2, linear filtering leads to aliasing artifacts due to high-frequency components of the source image leaking into the downsampled version. This manifests as temporal artifacts, where the contents of the texture appear to flicker as a triangle moves relative to the camera. This problem is commonly dealt with in image processing by widening the filter kernel so that its width is equal to the size of the downscaled pixel. So for instance if downscaling from 100×100 to 25×25, the filter kernel would be greater than or equal in width to a 4×4 square of pixels in the original image. Unfortunately widening the filter kernel isn’t usually a suitable option for realtime rendering, since the number of memory accesses increases with O(N2) as the filter width increases. Because of this a technique known as mipmapping is used instead. As any graphics programmer should already know, mipmaps consist of a series of prefiltered versions of a 2D texture that were downsampled with a kernel that’s sufficiently wide enough to prevent aliasing. Typically these downsampled versions are generated for dimensions that are powers of two, so that each successive mipmap is half the width and height of the previous mipmap. The following image from Wikipedia shows an example of typical mipmap chain for a texture:
当缩小倍数大于2时,线性滤波会导致一个走样错误,原因是原图的高频分量会泄露到缩小的贴图中。这显示为临时的瑕疵(K:貌似这样翻译有问题),当一个三角形相对于摄像机移动时,贴图的显示内容将会出现闪烁。这个问题,在图像处理中,通常的解决方法是扩大滤波器的核心,以致于它的宽度与缩小的倍数相等。举个例子,如果从100x100缩小到25x25时,滤波核心将会大于或者等于一个在原图中的4x4的像素区域。不幸的是,扩大滤波核心的方式并不适合于实时渲染,因为内存访问将因为滤波器宽度的增加,以O(N^2)增加。因为这个原因,被称为mipmapping的技术得到了应用。就如任何的图形程序员都已经知道的,这能够防止走样。通常情况下,这样的缩小的图像会以2的n次方来生成,以便连续的每个mipmap会是上一个mipmap的长宽的一半。下图来自Wikipedia,显示了一个贴图通常有的mipmap链:
An example of a texture with mipmaps. Each mip level is roughly half the size of the level before it. Image take from Wikipedia.
A box function is commonly used for generating mip maps, although it’s possible to use any suitable reconstruction filter when downscaling the source image. The generation is also commonly implemented recursively, so that each mip level is generated from the mip level preceding it. This makes the process computationally cheap, since a simple linear filter can be used at each stage in order to achieve the same results as a wide box filter applied to the highest-resolution image. At runtime the pixel shader selects the appropriate mip level by calculating the gradients of the texture coordinate used for sampling, which it does by comparing texture coordinate used for one pixel to the texture coordinate used in the neighboring pixels of a 2×2 quad. These gradients, which are equal to the partial derivatives of the texture coordinates with respect to X and Y in screen space, are important because they tell us the relationship between a given 2D image and the rate at which we’ll sample that image in screen space. Smaller gradients mean that the sample points are close together, and thus we’re using a high sampling rate. Larger gradients result from the sample points being further apart, which we can interpret to mean that we’re using a low sampling rate. By examining these gradients we can calculate the highest-resolution mip level that would provide us with an image size less than or equal to our sampling rate. The following image shows a simple example of mip selection:
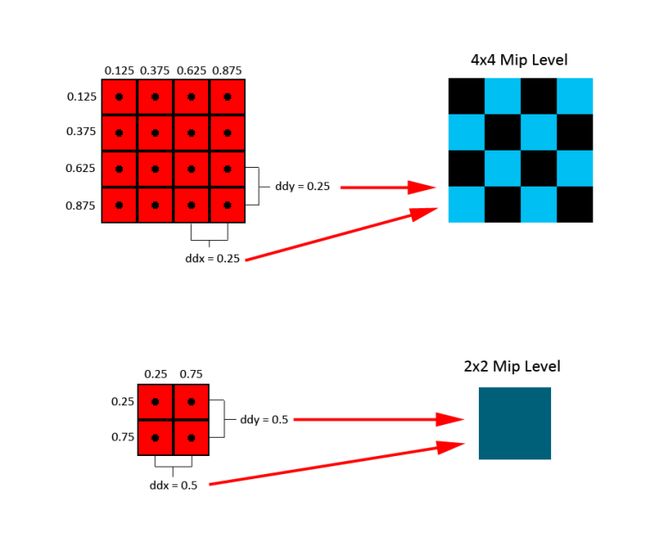
box function通常被用来生成mipmaps,尽管能够在缩小原图时,使用任何合适的reconstruction filter。这个生成的过程通常能够以递归的方式实现,以便每一个mip level都是通过上一个mip level来生成的。这样确保了这个计算过程是廉价的,因为一个简单线性滤波能够在每个stage中被应用,以便能够获得,像应用一个更宽的box filter到一个更高分辨率的图像中,一样的效果。在运行时,通过使用用于采样的纹理坐标来计算梯度值后,像素着色器会使用这个梯度值来选择合适的mip level。这个梯度值的计算,通过在一个2x2的方格中,先提取第一个像素的纹理坐标,再取其邻近的像素的纹理坐标进行比较而得到的。这个梯度值,与屏幕坐标上的X和Y方向上的偏导数是相等的,而且这个梯度值是很重要的,因为他们告诉我们,一个给定的2D图像和我们将要在屏幕空间上采样的比率之间的关系。更小的梯度值意味着采样点靠得更近,意味着我们使用着一个更高的采样率。更大的梯度值意味着采样点离得更远,意味着使用了一个更低的采样率。通过检查这些梯度值,我们能够利用最高分辨率的mip level计算出我们的图像尺寸,这个尺寸将会小于或者等于我们的采样率。下面的图像显示了一个mip 选择的简单例子:
In the image, the two red rectangles represent texture-mapped quads of different sizes rasterized to a 2D grid of pixels. For the topmost quad, the a value of 0.25 will be computed as the partial derivative for the U texture coordinate with respect to the X dimension, and the same value will be computed as the partial derivative for the V texture coordinate with respect to the Y dimension. The larger of the two gradients is then used to select the appropriate mip level based on the size of the texture. In this case, the length of the gradient will be 0.25 which means that the 0th (4×4) mip level will be selected. For the lower quad the size of the gradient is doubled, which means that the 1st mip level will be selected instead. Quality can be further improved through the use of trilinear filtering, which linearly interpolates between the results of bilinearly sampling the two closest mip levels based on the gradients. Doing so prevents visible seams on a surface at the points where a texture switches to the next mip level.
在这个图像中,两个红色的,经过纹理贴图的,大小不一样的四边形被光栅化为像素网格。上面的四边形,0.25是纹理坐标U在X方向上的偏导数,纹理坐标V在Y方向上的偏导数也和U相同。基于贴图的大小,两个中更大的那个梯度值被用来选择合适的mip level。在这个例子中,0.25的值表示第0层(4x4)的mip level将会被选择。下面的四边形中,梯度值是上面的两倍,这意味着第一层的mip level将会被选择。通过使用trilinear filtering质量会得到很大的提升,该trilinear filtering是基于梯度值选择两个最近的mip levels进行线性采样。当在两个不同的mip level进行切换时,这样做能够防止在表面上出现可见的裂缝。
One problem that we run into with mipmapping is when an image needs to be downscaled more in one dimension than in the other. This situation is referred to as anisotropy, due to the differing sampling rates with respect to the U and V axes of the texture. This happens all of the time in 3D rendering, particularly when a texture is mapped to a ground plane that’s nearly parallel with the view direction. In such a case the plane will be projected such that the V gradients grow more quickly than the U gradients as distance from the camera increases, which equates to the sampling rate being lower along the V axis. When the gradient is larger for one axis than the other, 3D hardware will use the larger gradient for mip selection since using the smaller gradient would result in aliasing due to undersampling. However this has the undesired effect of over-filtering along the other axis, thus producing a “blurry” result that’s missing details. To help alleviate this problem, graphics hardware supports anisotropic filtering. When this mode is active, the hardware will take up to a certain number of “extra” texture samples along the axis with the larger gradient. This allows the hardware to “reduce” the maximum gradient, and thus use a higher-resolution mip level. The final result is equivalent to using a rectangular reconstruction filter in 2D space as opposed to a box filter. Visually such a filter will produce results such that aliasing is prevented, while details are still perceptible. The following images demonstrate anisotropic filtering on a textured plane:
当一个维度上缩小的值比在另一个维度的多时,使用mipmapping的就会出现问题。这种情况被称为各向异性,这是由于在贴图的U和V方向上使用了不同的采样率。这种情况一直都出现在3D渲染中,尤其是当贴图映射到一个地平面上,这个地平面几乎与视觉方向平行。在这种情况下,当距离摄像机越远时,这个被投影的平面在V方向的梯度增长得比U方向的梯度要快,这和在V轴上的采样率更低是一样的道理。当梯度值在一个轴上比另一个轴要大时,3D硬件将会使用更大的梯度值用于选择相应的mipmap,因为使用更小的梯度将会因为缺少细节而出现走样。为了减轻这个问题,图形硬件支持anisotropic filtering(各向异性过滤)。当这个模式开启时,硬件将会在梯度值更大的轴上占据一定数量的额外纹理采样点(K:这个采样点的数量通常是我们说的2x,4x,8x,16x各向异性采样的值)。这允许硬件能够"减少"最大的梯度值,因为会用到更高的分辨率的mip level。在2D空间中,最终的结果将会和rectangular reconstuction filter相同,所谓的rectangular是相对于box来讲的。下面的图像展示了在一个贴图平面上的anisotropic filtering
A textured plane without anisotropic filtering, and the same plane with 16x anistropic filtering. The light grey grid lines demonstrate the distribution of pixels, and thus the rate of pixel shading in screen space. The red lines show the U and V axes of the texture mapped to plane. Notice the lack of details in the grain of the wood on the left image, due to over-filtering of the U axis in the lower-resolution mip levels.
一个没有anisotropic filter和一个有16x的anistropic filtering。浅灰色的网格线表示像素的分布,表示在屏幕空间中像素着色的比率。红线表示经过纹理映射后的平面的U和V轴。注意上图中缺少木纹理的贴图细节,原因是在U轴上使用了更低分辨率的mip levels。
(K:我在这里的理解是,U轴的梯度值一定比V轴要大得多的,所以V轴在没有各向异性的应用时,肯定用的是由U的梯度觉得的mip level的贴图,U越大,选取到的mip level将会越高,mip level的分辨率就会越低,相应的细节就会减少。)
Geometric Aliasing
几何走样
A second type of aliasing experienced in 3D rendering is known as geometric aliasing. When a 3D scene composed of triangles is rasterized, the visibility of those triangles is sampled at discrete locations typically located at the center of the screen pixels. Triangle visibility is just like any other signal in that there will be aliasing in the reconstructed signal when the sampling rate is inadequate (in this case the sampling rate is determined by the screen resolution). Unfortunately triangular data will always have discontinuities, which means the signal will never be bandlimited and thus no sampling rate can be high enough to prevent aliasing. In practice these artifacts manifest as the familiar jagged lines or “jaggies” commonly seen in games and other applications employing realtime graphics. The following image demonstrates how these aliasing artifacts occur from rasterizing a single triangle:
第二种走样的类型能够在3D渲染中经常遇到的是geometric aliasing(几何体走样)。当一个3D场景包含经过光栅化后的三角形时,这些可见的三角形在离散的位置上被采样,通常采样的位置会在屏幕像素的中心处。三角形的可见度(K:这个可见度应该说的是能够怎样在屏幕中被看到,而不是能不能看到)就如任何其他的信号一样,当采样率不精确时,将会在重建的信号中出现走样(在这个例子中,采样率是被屏幕分辨率决定的)。不幸的是,三角数据总是有不连续的,意味着信号将不会是bandlimited,因此没有任何的采样率能够防止走样的发生。实践中,这些人为瑕疵以锯齿状的线段或者“锯齿图形”显示出来,通常能够在游戏或者其他实时图形的应用程序中被看到。下面的图像展示了这些走样如何从光栅化后的三角形中发生:
Geometric aliasing occurring from undersampling the visibility of a triangle. The green, jagged line represents the outline of the triangle seen on a where pixels appear as squares of a uniform color.
Geometric aiasing发生在一个采样率过低的三角形上。绿色的,锯齿状的线段显示了三角形在同一颜色的四边形像素方格中如何被看到。
Although we’ve already established that no sampling rate would allow us to perfectly reconstruct triangle visibility, it is possible to reduce aliasing artifacts with a process known as oversampling. Oversampling essentially boils down to sampling a signal at some rate higher than our intended output, and then using those samples points to reconstruct new sample points at the target sampling rate. In terms of 3D rendering this equates to rendering at some resolution higher than the output resolution, and then downscaling the resulting image to the display size. This process is known as supersampling, and it’s been in use in 3D graphics for a very long time. Unfortunately it’s an expensive option, since it requires not just rasterizing at a higher resolution but also shading pixels at a higher rate. Because of this, an optimized form of supersampling known as multi-sample antialiasing (abbreviated as MSAA) was developed specifically for combating geometric aliasing. We’ll discuss MSAA and geometric aliasing in more detail in the following article.
尽管我们已经确定了,没有采样率能够允许我们完美地重建出三角形的可见度,但使用一个叫做oversampling的过程对于减低走样情况是可能的。Oversampling主要归结为使用一个更高的采样率去采样一个信号,相比于我们原来打算使用的采样率,然后使用那些采样点去重建出新的采样点。在3D渲染中,相比起使用原来输出的分辨率,使用一个更高的分辨率进行渲染,然后将采样得出的图像缩放到需要显示的大小。这个过程被称为supersampling,这已经在3D图形学中被使用了很长的一段时间了。很不幸的是,它是一个很昂贵的选项,因为它不只要求以更高的分辨率进行光栅化,并且以更高的比率进行像素着色。因为这个原因,一个supersampling的优化形式被称为multi-samle antialiasing(MSAA)被开发出来,用于改善geometric aliasing。我们将会在接下来的章节中对MSAA和geometric aliasing进行更多细节的讨论
Shader Aliasing
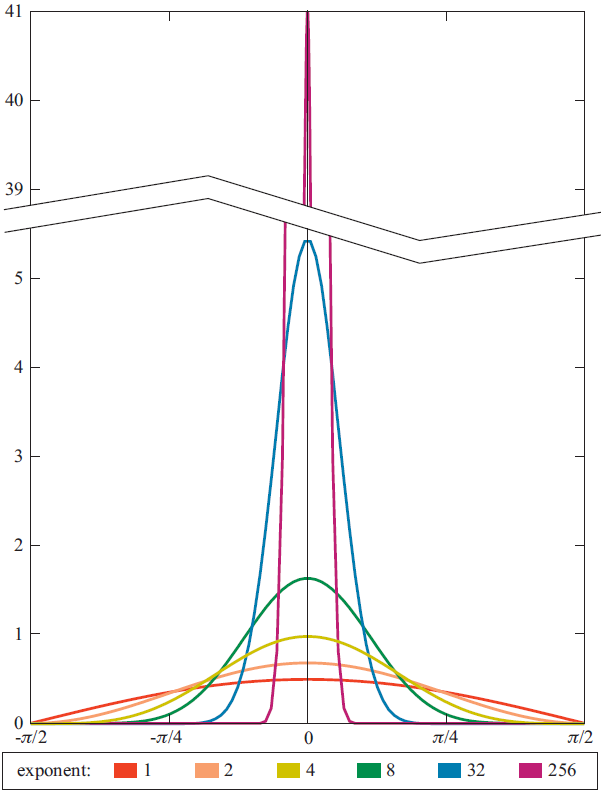
A third type of aliasing that’s common in modern 3D graphics is known as shader aliasing. Shader aliasing is similar to texture aliasing, in that occurs due to the fact that the pixel shader sampling rate is fixed in screen space. However the distinction is that shader aliasing refers to undersampling of signals that are evaluated analytically in the pixel shader using mathematical formulas, as opposed to undersampling of a texture map. The most common and noticeable case of shader aliasing results from applying per-pixel specular lighting with low roughness values (high specular exponents for Phong and Blinn-Phong). Lower roughness values result in narrower lobes, which make the specular response into a higher-frequency signal and thus more prone to undersampling. The following image contains plots of the N dot H response of a Blinn-Phong BRDF with varying roughness, demonstrating it becomes higher frequency for lower roughnesses:
3D图形学中常见的第三种走样被称为shader aliasing(着色器走样)。Shader aliasing类似于texture aliasing,它们发生的原因在于像素的着色采样率在屏幕空间上是固定的。然而,它们的区别在于,shader aliasing是信号使用数学公式,在像素着色计算的过程中采样过低,而texture aliasing是用于对贴图映射采样过低(K:就如,在pixel shader中,需要根据采样的数据,如光栅化后插值出来的数据,应用到一个连续的函数中,那么这个连续的函数由于采样过低,肯定不能够在这个固定的采样率下完美地还原出这个连续的函数应有的样子,就出现了所谓的shader aliasing,而texture aliasing相当于把连续的数学公式需要计算的值已经预先计算好在texture中)。最常见并且最让人主要到的shader aliasing是,使用低粗糙度值(Phong和Blinn-Phong中的高specular指数)在逐像素高光中的计算(K:粗糙度值就相当于Phong光照模型中的specular的power指数值)。更低的粗糙度值会产生出更窄的波瓣,这会让高光响应变成一个更高频的信号,因此更倾向于出现采样过低。下面的图像包含了N dot H的响应值与不同的粗糙值在Blinn-Phong BRDF中绘制的图像,这展示了越低的粗糙度会有越高的频率值:
N dot H response of a Blinn-Phong BRDF with various exponents. Note how the response becomes higher-frequency for higher exponents, which correspond to lower roughness values. Image from Real-Time Rendering, 3rdEdition, A K Peters 2008
Shader aliasing is most likely to occur when normal maps are used, since they increase the frequency of the surface normal and consequently cause the specular response to vary rapidly across a surface. HDR rendering and physically-based shading models can compound the problem even further, since they allow for extremely intense specular highlights relative to the diffuse lighting response. This category of aliasing is perhaps the most difficult to solve, and as of yet there are no silver-bullet solutions. MSAA is almost entirely ineffective, since the pixel shading rate is not increased compared to the non-MSAA. Supersampling is effective, but prohibitively expensive due to the increased shader and bandwidth costs required to shade and fill a larger render target. Emil Persson demonstrated a method of selectively supersampling the specular lighting inside the pixel shader[6], but this too can be expensive if the number of lights are high or if multiple normal maps need to be blended in order to compute the final surface normal.
当normal maps被使用时,Shader aliasing是最可能会发生的,因为他们增加了表面法向的频率,因此导致了高光响应会在整个表面上快速变化。HDR和基于物理着色模型会使这个问题变得更复杂,因为它们允许强度非常大的高光出现,相对于散射光的响应来讲。这种走样可能是最难以分辨出来的,到目前为止,还没有有效的解决方法。MSAA几乎是完全失效的,因为像素的着色率没有相应的增加(K:MSAA只会计算一次shader)。Supersampling是有效的,而鉴于着色计算和用于填充更大的RT的带宽可能消耗太大。Emil Persson展示了一个方法,在像素着色中,有选择地对高光的处理进行supersampling,但这也会变得昂贵,如果灯光的数量太多或者多个normal maps需要混合以计算出表面最终的法线。
A potential solution that has been steadily gaining some ground[7][8] is to modify the specular shading function itself based on normal variation. The theory behind this is that microfacet BRDF’s naturally represent micro-level variation along a surface, with the amount of variation being based on a roughness parameter. If we increase the roughness of a material as the normal map details become relatively smaller in screen space, we use the BRDF itself to account for the undersampling of the normal map/specular lighting response. Increasing roughness decreases the frequency of the resulting reflectance, which in turn reduces the appearance of artifacts. The following image contains an example of using this technique, with an image captured with 4x shader supersampling as a reference:
一个潜在的解决办法已经持续得到支持,它根据法线的变化,修改高光着色函数自身来达到目的。这背后的原理是,微表面的BRDF原生地呈现着一个表面的微观变化,而微观变化有多少是依赖于粗糙度参数的。如果我们增加一个材质的粗糙度,那么在屏幕空间中,normal map的细节就会相对变得更小,我们使用BRDF自身,导致normal map或specular lighting response处于采样不足的状态。增加粗糙度会降低反射的频率,转而降低表面的人工痕迹。下面的图像包含了使用这个技术的一个例子,与一个使用了4x shader supersamping作为参考:
The topmost image shows an example of shader aliasing due to undersampling a high-frequency specular BRDF combined with a high-frequency normal map. The middle image shows the same scene with 4x shader supersampling applied. The bottom image shows the results of of using a variant of CLEAN mapping to limit the frequency of the specular response.
最上面的图像显示了一个shader aliasing的例子,它是由于一个高频的高光BRDF结合了高频的normal map而出现的采样不足。中间的图像显示了相同的场景下,使用4x shader supersampling。下面的图像显示了使用一个可变的CLEAN映射去限制高光响应频率的例子。
This approach (and others like it) can be considered to be part of a broader category of antialiasing techniques known as prefiltering. Prefiltering amounts to applying some sort of low-pass filter to a signal before sampling it, with the goal of ensuring that the signal’s bandwidth is less than half of the sampling rate. In a lot of cases this isn’t practical for graphics since we don’t have adequate information about what we’re sampling (for instance, we don’t know what triangle should is visible for a pixel until we sample and raterize the triangle). However in the case of specular aliasing from normal maps, the normal map contents are known ahead of time.
这个方法(或者其他类似的)能够被认为是广泛反走样计算范畴的一部分,被称为prefiltering。Prefiltering相当于在采样某个信号前,应用某些类型的低通滤波器到一个信号中,目的是为了保证信号的带宽小于采样率的一半。在很多的情况下这并不适合图形学,因为我们对要采样的东西,无法获得精确的信息(例如,我们不知道三角形会怎样以一种像素的形式被观察,直到我们采样和光栅化这个三角形)。然而来自于normal maps下的高光走样,这个normal map的内容我们却能够预先知道的。
Temporal Aliasing
时域走样
So far, we have discussed graphics in terms of sampling a 2D signal. However we’re often concerned with a third dimension, which is time. Whenever we’re rendering a video stream we’re also sampling in the time domain, since the signal will completely change as time advances. Therefore we must consider sampling along this dimension as well, and how it can produce aliasing.
到目前为止,我们都以采样2D信号的形式讨论图形学。然而,我们经常需要关心第三维,那就是时间。无论什么时候我们渲染一个视频流我们也在时域上进行采样,从这个时候起,信号会在时间流逝的过程中完全改变。所以我们也必须考虑在这个维度上的采样,和它是怎样产生走样的。
In the case of video we are still using discrete samples, where each sample is a complete 2D image representing our scene at some period of time. This sampling is similar to our sampling in the spatial domain: there is some frequency of the signal we are sampling, and if we undersample that signal aliasing will occur. One classic example of a temporal aliasing is the so-called “wagon-wheel effect”, which refers to the phenomenon where a rotating wheel may appear to rotate more slowly (or even backwards) when viewed in an undersampled video stream. This animated GIF from Wikipedia demonstrates the effect quite nicely:
在视频的例子中,我们仍然使用离散的采样,在那里,每个采样都是一个完整的2D图像,用于显示我们场景在某个时间的样子。这个采样类似于我们在时域上的采样:有一些信号的频率是我们正在采样的,如果我们采样不足,走样就会发生。一个关于时域走样的经典例子被叫做“wagon-wheel effect”,它提及到的现象是,当在一个采样不足的视频流中观看时,一个旋转的车轮可能会出现旋转得越来越慢(甚至是反向的)。下面的来自Wikipedia的GIF很好地展示了这个情况:
A demonstration of the wagon-wheel effect that occurs due to temporal aliasing. In the animation the camera is moving to the right at a constant speed, yet the shapes appear to speed up, slow down, and even switch direction. Image taken from Wikipedia.
一个因为temporal aliasing而发生wago-wheel effect的事例。在这个动画中,摄像机正在以恒定的速度往右移动,然而里面的形状却是逐渐加速,降低,和甚至方向反转。图像是从Wikipedia中引用的。
In games, temporal sampling artifacts usually manifest as “jerky” movements and animations. Increases in framerate correspond to an increase in sampling rate along the time domain, which allows for better sampling of faster-moving content. This is directly analogous to the improvements that are visible from increasing output resolution: more details are visible, and less aliasing is perceptible.
在游戏中,temporal sampling的人为痕迹通常表现在移动和动画的特然跳动。在时域上,增加帧率,相对应于增加采样率,这对于一个快速移动的内容来讲,会有一个更好的采样表现。这相当于直接模拟,通过增加输出的分辨率来提高可视质量:更多的细节被看到,预期更少的走样。
The most commonly-used anti-aliasing technique for temporal aliasing is motion blur. Motion blur actually refers to an effect visible in photography, which occurs due to the shutter of the camera being open for some non-zero amount of time. This produces a result quite different than what we produce in 3D rendering, where by default we get an image representing one infinitely-small period of time. To accurately simulate the effect, we could supersample in the time domain by rendering more frames than we output and applying a filter to the result. However this is prohibitively expensive just like spatial supersampling, and so approximations are used. The most common approach is to produce a per-pixel velocity buffer for the current frame, and then use that to approximate the result of oversampling with a blur that uses multiple texture samples from nearby pixels. Such an approach can be considered an example of advanced reconstruction filter that uses information about the rate of change of a signal rather than additional samples in order to reconstruct an approximation of the original sample. Under certain conditions the results can be quite plausible, however in many cases noticeable artifacts can occur due to the lack of additional sample points. Most notably these artifacts will occur where the occlusion of a surface by another surface changes during a frame, since information about the occluded surface is typically not available to the post-process shader performing the reconstruction. The following image shows three screenshots of a model rotating about the camera’s z-axis: the model rendered with no motion blur, the model rendered with Morgan McGuire’s post-process motion blur technique[9] applied using 16 samples per pixel, and finally the model rendered temporal supersampling enabled using 32 samples per frame”
运动模糊经常使用针对temporal aliasing的反走样技术。现实生活中,在摄影中能够看到运动模糊的效果,它的发生是因为摄像机的快门在某个很短的时间下打开(K:想象一下,你将相机的快门时间调高,然后对一个运动的物体拍摄,产生出的效果就是模糊的)。这产生的结果和我们在3D渲染中产生的结果有很大不同,默认地,我们获得的图像,表示的是在一个无穷小的时间内显示的内容(K:而在3D渲染就不一样了,你在某个时间点截图的图像是不可能有任何模糊的,每一个像素都恰当的显示在当前的采样时间上,图像会是非常清晰的)。为了精确的塑造这个效果,我们可以在时域进行supersampling,通过渲染更多的帧数并应用一个filter到这个结果中。然而,这是太昂贵而被禁止的,就如空间上的supersampling一样,所以一个近似的方法被用上了。最常用的方法是,对当前帧产生一个逐像素的移动速度到一个buffer中,然后使用这个近似的结果进行oversampling,这个oversampling会带有模糊效果,它会使用到多个贴图的样本,这些样本都是来自采样点旁边的像素。这种方法被认为是高级的reconstruction filter的例子,为了能够重建出接近原始采样数据,它会使用信号的变化率作为信息而不是额外的采样点。在某些条件下,这个结果是十分可信的,然而在很多情况下,能让人注意到的人工痕迹将会发生,原因在于缺失了额外采样点。最让人主要到是,这些痕迹将会在一帧中,在一个表面遮挡另一个表面的关系发生变化时(K:如本来是A遮挡B的,这帧中会变成B遮挡A)被观察到,因为这些关于遮挡表面的信息通常在后处理着色器执行重建中是不可用的。下面的图像显示了三个模型沿着摄像机z轴进行旋转的屏幕截图,第一个没有使用运动模糊,第二个使用了 Morgan McGuire’s post-process motion blur technique,每个像素应用了16个采样点,第三个图使用了temporal supersampling每帧启用了32个采样点:
A model rendered without motion blur, the same model rendered with post-process motion blur, and the same model rendered with temporal supersampling.
References
[1]Hou, Hsei. Cubic Splines for Image Interpolation and Digital Filtering. IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 26, Issue 6. December 1978.
[2]Mitchell, Don P. and Netravali, Arun N. Reconstruction Filters in Computer Graphics. SIGGRAPH ’88 Proceedings of the 15th annual conference on Computer graphics and interactive techniques.
[3]http://entropymine.com/imageworsener/bicubic/
[4] Schreiber, William F. Transformation Between Continuous and Discrete Representations of Images: A Perceptual Approach. IEEE Transactions on Pattern Analysis and Machine Intelligence. Volume 7, Issue 2. March 1985.
[5] Brown, Earl F. Television: The Subjective Effects of Filter Ringing Transients. February, 1979.
[6]http://www.humus.name/index.php?page=3D&ID=64
[7]http://blog.selfshadow.com/2011/07/22/specular-showdown/
[8]http://advances.realtimerendering.com/s2012/index.html
[9]McGuire, Morgan. Hennessy, Padraic. Bukowski, Michael, and Osman, Brian. A Reconstruction Filter for Plausible Motion Blur. I3D 2012.