pytorch教程 (四)- 损失函数
在深度学习项目中首先对数据做数据预处理,然后构建模型之后,第三步需要定义一个好的损失函数。
配置损失函数都是确保模型以预期方式工作的最重要步骤之一。 损失函数可以为神经网络提供很多实用的灵活性,它将定义网络输出与网络其余部分的连接方式。
简单说损失函数(J)可以定义为具有两个参数的函数:
- 预测输出
- 真实输出
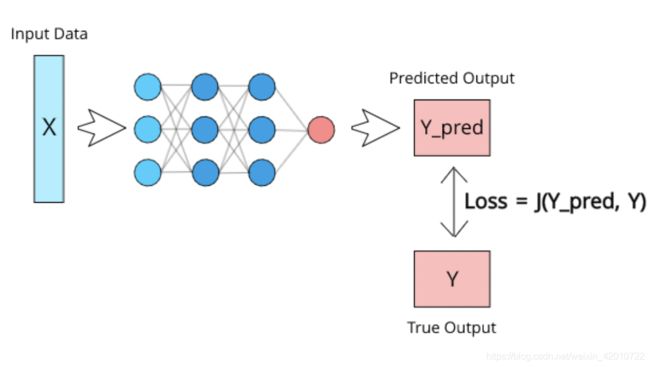 定义损失函数,通过将模型的预测值与真实值进行比较,比较二个值之间的差距,差距越小,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
定义损失函数,通过将模型的预测值与真实值进行比较,比较二个值之间的差距,差距越小,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
一般来说,监督学习的目标函数由二部分组成:
o b j e c t i v e = L o s s + R e g u l a r i z a t i o n objective=Loss+Regularization objective=Loss+Regularization
- 对于回归模型,通常使用的内置损失函数是均方损失函数nn.MSELoss 。
- 对于二分类模型,通常使用的是二元交叉熵损失函数nn.BCELoss (输入已经是sigmoid激活函数之后的结果) 或nn.BCEWithLogitsLoss (输入尚未经过nn.Sigmoid激活函数)
- 对于多分类模型,一般推荐使用交叉熵损失函数 nn.CrossEntropyLoss。 (y_true需要是一维的,
是类别编码。y_pred未经过nn.Softmax激活。
pytorch损失函数
- 传统深度学习损失函数
-
- 分类损失
-
- 二分类
- 多分类
- 多标签分类
- 回归损失
传统深度学习损失函数
分类损失
二分类
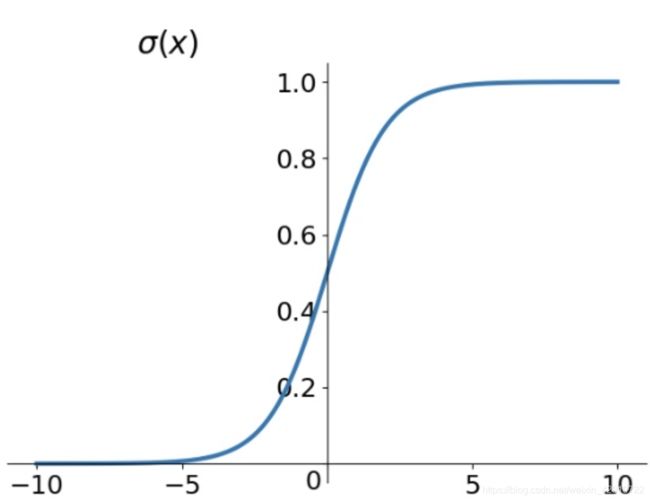
在进行两个类之间的预测,通常让模型输出一个概率值,通过概率值阈值来判断,我们的样本属于那一类,通过概率判断属于哪一类需要用到一个激活函数,常见的使用S型函数,该函数将任何实际值压缩到0到1之间
由上图S函数图可知,随着sigmoid的输入变大并趋于正无穷大,的输出趋向于1。输入变小而趋向于负无穷大,输出将趋于0。现在我们保证总是得到一个介于0到1之间的值
在二分类中,我们可以认为一类为正样本,一类为负样本。
如果输出高于0.5(概率为50%),我们将认为它属于正类别;如果输出低于0.5,则我们将认为它属于负类别。例如,如果我们正在训练一个在猫和狗之间进行分类的网络,则可以为狗分配正类,并且在狗的数据集中的输出值将为1,类似地,将为猫分配负类,而对猫的输出值将为为0。
我们用于二进制分类的损失函数称为二进制交叉熵(BCE)。该功能有效地惩罚了用于二进制分类任务的神经网络

由上图可知:
正样本(Y=1)的损失函数为: L o s s = − l o g ( Y p r e d ) Loss = -log(Y_pred) Loss=−log(Ypred)
负样本(Y=0)的损失函数为: L o s s = − l o g ( 1 − Y p r e d ) Loss = -log(1-Y_pred) Loss=−log(1−Ypred)
由此总的损失函数为:
L o s s = ( Y ) ( − l o g ( Y p r e d ) + ( 1 − Y ) ( − l o g ( 1 − Y p r e d ) ) ) Loss=(Y)(-log(Y_{pred})+(1-Y)(-log(1-Y_{pred}))) Loss=(Y)(−log(Ypred)+(1−Y)(−log(1−Ypred)))
在pytorch api中常用的损失函数:
torch.nn.BCELoss:(二元交叉熵,用于二分类,输入已经过nn.Sigmoid激活,对不平衡数据集可以
用weigths参数调整类别权重)
torch.nn.BCEWithLogitsLoss:(二元交叉熵,用于二分类,输入未经过nn.Sigmoid激活)
多分类
当我们需要我们的模型每次预测一个可能的类输出时,多分类是合适的。 现在,由于我们仍在处理概率,因此将sigmoid应用于所有输出节点可能有意义,这样我们对于所有输出都获得介于0到1之间的值,但这是有问题的。 在考虑多个类别的概率时,我们需要确保所有单个概率的总和等于1,因为这是定义概率的方式。 应用S形(sigmoid)不能确保总和始终等于1,因此我们需要使用另一个激活函数。
我们在这种情况下使用的激活函数是softmax。 此功能确保所有输出节点的值都在0-1之间,并且所有输出节点值的总和始终等于1。 softmax的公式如下:
S o f t m a x ( y i ) = e y i ∑ i = 0 n e y i Softmax(y_{i})=\frac{e^{y_{i}}}{\sum_{i=0}^n{e^{y_{i}}}} Softmax(yi)=∑i=0neyieyi
在pytorch api中常用的损失函数:
torch.nn.CrossEntropyLoss:(交叉熵,用于多分类,要求label为稀疏编码,输入未经过
nn.Softmax激活,对不平衡数据集可以用weigths参数调整类别权重)
torch.nn.NLLLoss:(负对数似然损失,用于多分类,要求label为稀疏编码,输入经过
nn.LogSoftmax激活)
torch.nn.CosineSimilarity:(余弦相似度,可用于多分类)
多标签分类
当模型需要预测多个类别作为输出时,便完成了多标签分类。 例如,假设您正在训练神经网络,以预测某些食物图片中的成分。 我们需要预测多种成分,因此Y中将有多个1’。
为此,我们不能使用softmax,因为softmax始终只会迫使一个类别变为1,而其他类别变为0。因此,由于我们试图预测每个类别的个体概率,因此可以简单地在所有输出节点值上保持sigmoid。
至于损失,我们可以直接在每个节点上使用对数损失进行求和,类似于在多类分类中所做的。
回归损失
在回归模型中,我们的神经网络将为每个我们试图预测的连续值提供一个输出节点。 通过在输出值和真实值之间进行直接比较来计算回归损失。
我们用于回归模型的最流行的损失函数是均方误差损失函数。 在此,我们仅计算Y和Y_pred之差的平方,并对所有数据求平均值。 假设有n个数据点:
L o s s = 1 n ∗ ∑ i = 0 n ( Y i − Y p r e d i ) 2 Loss=\frac{1}{n}*\sum_{i=0}^n{(Y_{i}-Y_{pred_{i}})}^2 Loss=n1∗∑i=0n(Yi−Ypredi)2
均方误差损失函数
在这里,Y_i和Y_pred_i指的是数据集中第i个Y值,以及来自神经网络的相同数据的相应Y_pred
在pytorch api中常用的损失函数:
torch.nn.MSELoss:(均方误差损失,也叫做L2损失,用于回归)
torch.nn.L1Loss:(L1损失,也叫做绝对值误差损失,用于回归)
torch.nn.Smooth1Loss:(平滑L1损失,当输入在-1到1之间时,平滑为L2损失,用于回归)