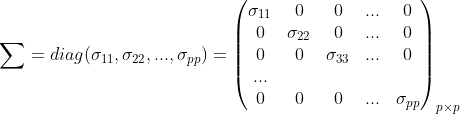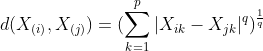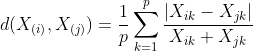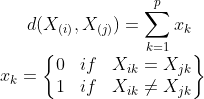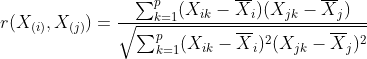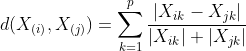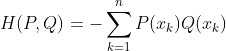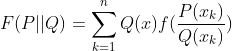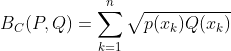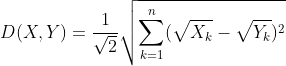相似性度量（距离度量）方法（一）：基本种类与公式

相似性度量（或距离度量）方法在多元统计中的聚类分析、判别分析中的距离判别法、泛函分析、机器学习等方面都有应用。所以对于数据分析、机器学习等方面，掌握相似性的不同度量方法是十分重要且必要的。

相似性度量与距离度量本质上是同一件事情。如果两组数据之间的距离越大，那么相似性越小；反正，如果相似性越大，那么距离越小，这是可以直观理解的。

但是距离度量与相似度量还是有一点点区别的。距离度量，一般情况下距离是大于0的数；而相似性或相异性通常数值介于[0,1]之间。相似性与相异性统称为邻近度。

对于相似性的度量，首先我们需要了解我们需要度量的对象，即样本中的数据。对于数据我们可以用样本数据矩阵（观测值矩阵）来表示，即：

这里p表示数据维数（变量个数），即变量的个数p；n是数据的个数,其中

表示第i组数据（在多元统计中，各个量通常用列向量表示，数据也是如此）。而对于距离（相似性）度量，研究的就是两组数据之间的距离。

除了研究样本中两个数据之间距离，还有集合之间距离、概率分布之间距离、变量之间距离、序列之间的距离等。

兔兔在下面将介绍一些距离度量方法。

（1）欧式距离。

欧式距离也是最常用的距离度量方法，从直观上理解就是两点间的直线距离。

上式表示的就是数据与之间的欧式距离。当p=1时，就是数轴上两个点的距离（即绝对值）；当p=2时，就是平面两点间直线距离；p=3时，即空间两点之间的直线距离。p>3,就是p维空间的两点距离，所以欧式距离具有很好的直观性，便于理解。

import numpy as np
X1=[10,12,3] #第一组数据
X2=[10,2,4] #第二组数据
def Euclidean_distance(X1,X2):
    '''计算欧式距离'''
    p=len(X1) #数据的维数
    s=0
    for i in range(p):
        s+=(X1-X2)**2
    return np.sqrt(s)
distance=Euclidean_distance(X1,X2)
print(distance)

以上是计算欧式距离的函数与实例代码。

（2）平方欧式距离。

平方欧式距离，顾名思义就是把欧式距离的结果平方，得到的就是平方欧式距离。即：

其结果也可以用向量乘积表示。对于算法实现，只要把上一个的开平方去掉即可，也可以用numpy中向量乘积的方法。

（3）标准化后的欧式距离。

对于前面讲到的欧式距离，也是有局限性的。比如，如果向量中各个单位不全相同，则欧式距离一般情况下就没有意义，即使单位全相同，但如果各个分量变异性相差很大，则变异性很大的的分量在欧式距离中起决定性作用，而变异性小的几乎不起作用。所以可以先对数据标准化，再计算欧式距离。

其中标准化是指一组数据减去样本总体的均值，再除以对应变量的方差的开平方（即除以标准差）。第一个式子是第i组数据第j个指标的标准化，即用Xij减去第j个变量的均值，再除以第j个变量的标准差，第二个是标准化后第i组数据。之后就可以根据标准化后的数据来计算距离了。

（4）马氏距离（广义欧式距离）。

标准化后计算欧式距离，虽然消除了各个变量（或指标）的单位或方差的影响，但是无法消除变量之间的相关性的影响。所以我们就引入了马式距离来消除这种相关性的影响。马式距离也是多元统计分析中比较常用的距离度量方法。

其中表示样本X的协差阵的逆矩阵，表示样本协差阵。

（5）平方马式距离。

平方马式距离即把马式距离进行平方。式子就是上面的等式右边，把根号去掉。

注：关于马式距离的一些性质：

（1）若

即样本各个分量不相关，此时的马式距离就是各个分量经标准化后的欧式距离；平方马式距离就是标准化后的平方欧式距离（即马式距离退化成加权欧式距离，对应（3））。

（2）经单位变换后为（，C为常矩阵，b为常向量）。马氏距离保持不变。

（3）马氏距离不受变量单位的影响，是一个无单位的数值。

（6）绝对距离（曼哈顿距离）。

从直观上来看就是两组数据对应变量之差的绝对值，之后再求和。它的实际意义相当于从一个十字路口到另一个十字路口的距离。

（7）切比雪夫距离。

即两组数据对应的变量之差的绝对值最大的那个数。

（8）明考夫斯基距离（明氏距离、闵氏距离、闵可夫斯基距离）。

明氏距离实际上是欧式距离、绝对距离、切比雪夫距离的一般形式。

我们发现，当q=1时，就是绝对距离；q=2时，就是欧式距离；q=时，就是切比雪夫距离。

（9）兰氏距离。

兰氏距离适用于一切的情况，可以克服各指标之间量纲的影响；对大的奇异值不敏感，特别适合高度偏倚的数据；但是它没有考虑指标之间的相关性。

（10）海明（汉明）距离。

海明距离主要用于信息编码中距离的度量，例如在免疫算法中就会用到这个距离。海明距离就是两个等长字符串对应位置不同字符的个数。

例如对应两个数组[1,1,0,0,0]和[0,1,0,1,0],它们对应位置元素不同的位置是1、2、4，所以海明距离就是3。

汉明距离缺点是，当两个向量长度不等时，就很难使用了。

（11）余弦相似度。

余弦相似度经常用于解决高维欧几里得距离问题。其数值介于[-1,1]之间，也就是余弦函数的值域。

式子表示的就是两组数据（两个向量）之间的夹角余弦。所以它的缺点就是不考虑向量的大小，只考虑方向，在实践中，这意味着没有完全考虑值的差异所以容易出现问题。余弦相似度通常在高维数据并且向量大小不重要时使用，而且对于文本分析问题，当数据由字数表示时，该方法就非常常用。

（12）杰卡德指数（Jaccard Index)。

Jaccard指数用于计算样本集的相似性和多样性度量。而计算杰卡德距离，只需要用1减去杰卡德指数即可。

杰卡德距离主要缺点是受数据大小的影响很大，大型数据对索引会产生很大影响，因为它可以显著增加并集，同时保存交集相似。而且杰卡德距离主要用于集合之间的距离度量。例如集合A={1，2，3，4，5}，集合B={6，1，2，3}，那么两个集合的交集有3个元素，并集有6个，那么杰卡德指数就是3/6=0.5，杰卡德距离就是1-0.5=0.5.

（13）相关系数。

利用两个样本的相关系数也可以用作距离度量的方法。两组数据的相关系数可以由样本的相关阵来确定，也可以由下面式子计算：

上式即为两组数据的相关系数。其中分别代表第i、j组数据的均值。相关系数数值在[-1,1]之间，表示两组数据相似程度。如果|r|=1,说明完全相似；|r|接近于0，说明差别很大；如果等于0，就说明完全不相似。

在相关系数的基础上，我们可以变换为距离度量，即

或：

这样就可以表示两组数据之间的距离。距离越远，即越不相似。

注：事实上，由距离度量构造相似系数总是可能的。如,但是由相似系数构造距离却不总是可行的。

（14）半正弦（Haversine distance)距离.

该方法表示的是给定经度和维度的球体上两点之间的距离。该距离在数据处理、机器学习中几乎用到，主要用于导航等问题。而且公式、计算也比较复杂，而且很难处理多维数据，与之对应的是Vincenty距离，表示的是椭球上两点距离。所以兔兔就不把这些公式列出了，感兴趣的同学可以在网上搜索。

（15）Sorensen-Dice系数。

该系数与Jaccard系数非常相似，但是该系数更直观一些，它表示两个集合之间的重叠百分比，介于0~1之间。用1减去该系数就可以表示Sorensen-Dice距离。

与Jaccard距离相似，该距离通常用于图像分割任务或文本相似性分析。

（16）布雷柯蒂斯（Bray-Curtis)距离。

该距离通常用于生态学、环境科学中定义距离，取值在[0,1]之间。

（17）堪培拉（Canberra）距离。

堪培拉距离通常对接近0的数值变换非常敏感。与马式距离一样，对数据量纲不敏感。但是它没有考虑变量之间相互独立性与变量之间的相关性它可以看成是曼哈顿距离的加权版本。

（18）Tanimoto距离。

Tanimoto距离也称为Tanimoto测度，可用于实向量的测量，也可以用于离散值向量测量。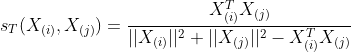

这里Xi与Xj两个向量越相似，s数值越大，也就是距离越近。

（19）相对熵（KL散度）。

从这里开始，距离和之前就有很大本质上的不相同。因为前面的距离都满足距离的定义，即满足对称性与三角不等式。例如a与b的距离等于b与a的距离，d(a,b)+d(b,c)>=d(a,c)等等。而从相对熵这里开始，距离便不再满足对称性与三角不等式。与其说是距离，其实更准确来讲是一种损失函数，即在机器学习中衡量两个函数的相近程度，判断预测值与实际值的差别，这种差别（或相近程度）可以看作是一种“距离”。但是从数学角度出发，它并不满足距离的定义。

其中的P(x)、Q(x)分别表示两种概率分布的概率密度函数，如果交叉熵越小，说明分布P与分布Q越接近。第一个式子表示的是离散型概率分布的相对熵，第二个表示的是离散型概率分布的相对熵。而在机器学习中，我们通常把向量x通过函数来变换成0~1之间是数，也就变成了概率，并且其中P(x)表示的是真实的概率分布（或真实的值,label)，而Q(x)表示理论拟合出来的预测值，x表示每一组数据的向量，根据第一个式子就是n组数据处理后求和。我们目的就是减少理论预测值与实际值label之间的距离，也就是减少相对熵。所以从本质上来说，交叉熵是损失函数的一种构造方法。

举例：

例如P(x)的概率分布（一元离散概率分布）为：

X	1	2	3
P（X）	0.1	0.1	0.8

Q(x)概率分布为：

X	1	2	3
Q（X）	0.2	0.3	0.5

那么D（P||Q）=。

事实上，可以发现D(P||Q)D(Q||P)。并且相对熵始终大于零。

注：关于相对熵的一些性质：

（1）关于相对熵、熵与交叉熵的关系。

其中H（P）表示熵（entropy),H(P,Q)表示交叉熵（cross entropy)。对应的就是式子积分的左半部分与右半部分。（对应离散的情况，把积分换成求和即可）。

（20）交叉熵。

交叉熵也常常用于机器学习中分类问题，评估实际值label与预测prediction之间的距离。

这里的交叉熵也就是（19）中相对熵的组成部分。

（21）JS散度。

JS散度也叫做JS距离，是KL散度的一种变形。

其中KL表示的就是（19）中的相对熵。JS散度取值范围为[0,1]，两个随机变量分布相同是1，相反是1。也就是值越大，两个分布相差越远。

（22）F散度。

F散度是一个函数，衡量两个分布P，Q之间的区别。

其中函数f(x)需要满足：f(x)为凸函数，并且f(1)=0。并且，当，F散度就变成了KL散度；当，那么就变成reverse KL散度。以下是常用的f(x)函数与对应的散度。

散度	f(x)
KL-散度
Pearson  散度
Neumann  散度
α-散度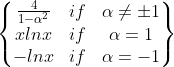
α-散度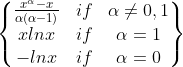
Hellinger 距离
Total variation distance

reverse KL 散度

（23）巴氏距离。

巴氏距离（巴塔恰里雅距离，Bhattacharyya distance）用于测量两个离散概率分布，常在分类中测量类之间的可分离性。

其中表示巴氏系数，介于[0,1]之间，表示巴氏距离，为0到正无穷之间的数。

（24）Hellinger 距离。

该距离被用来衡量两个概率分布之间的相似性，属于F散度中的一种。

这里X,Y代表两组变量（两个概率分布），n是数据个数。

（25）逐点互信息。

逐点互信息衡量两个事物的相关性。设事件A,B发生概率为p(x),p(y),两个事件同时发生概率为p(x,y)，则：

并且，两个事件相关性越大，则PMI越大（也就是距离越小）。并且根据条件概率，该式也可以写成：.

PMI在机器学习中经常用于衡量模型训练之后label与prediction的关系。

（26）pearson系数。

pearson系数用于度量两个变量之间的相关性，就是线性相关性，值为[-1,1]。

x，y表示两个变量（指标）。相关性越大，值越大，距离就越小。

（27）Ochiai系数。

这个系数是余弦相似度的一种形式，衡量两个集合的相似程度。

|A|表示的是集合A的大小。

（28）Hausdorff距离。

该距离主要用于衡量两个点集合之间的距离。

对于点集合A={a1,a2,...},B={b1,b2,...}，集合A,B距离表示为：

其中称为双向Hausdorff距离，为从点集A到点集B的单向Hausdorff距离，d(a,b)表示两点之间距离度量方法，通常用欧式距离。对于h(A,B),实际上就是先计算A集合中ai点到B集合各个点的距离，找最短的那个距离，然后再从这些最短距离当中找最长的那个距离。（关于深入理解与算法实现，兔兔在第二篇当中会详细说明）。

（29）Levenshtein距离。

这个距离用于计算两个字符串之间的距离。与汉明距离不同，它可以计算长度不同的序列距离，所以它也可以用于度量两个DNA序列之间的相似性（距离），也可以在自然语言处理中计算字之间的距离。

它的度量方式是看至少需要多少次处理能把一个字符串变成另一个字符串。所以该距离也称为编辑距离（Edit Distance)，设两个字符串a,b,长度为|a|,|b|,则它们的Levenshtein距离为：

很明显，它的算法结构是一种递归形式，只要函数中有递归表达式与终止条件，该算法便可以实现。Sim表示两个字符串的相似度。其中时第四个式子后面+1，如果相等就是+0。

（30）含名义变量样本的相似性度量。

对于含有名义变量的样本，我们可以记对应变量取值相同的个数为m1，不同的为m2，则样本距离定义为：

例如 ，对于学员资料，两个学员信息如下：

X1	男	英语	统计	非教师	校外	本科
X2	女	英语	金融	教师	校外	本科以下

那么X1与X2配合的个数是2，不配合（不相同）的个数是4，则距离为d=4/6=2/3。其实该度量方法本质上就是汉明距离。

除了上述方法，也可以用Jaccard系数，把两个数据看成两个集合来计算。而且针对二进制属性，有序变量、混合型属性等等，也有很多的相应度量方法。

总结：

在本文中，针对研究对象的不同，我们采用了不同的距离度量方法，并且每一种研究对象一般都有多种不同的度量方法。这些公式大部分比较好理解，也容易用算法实现。但其中也有一些需要深入的理解，并且需要引入一些相关的基础知识。所以兔兔会在第二篇进行进一步讲解。