2022 第五届 浙江省大学生网络与信息安全竞赛技能赛 决赛密码wp

CRYPTO

math

key为n-1的阶乘，由威尔逊定理得$key\ast (n-1)=1\%n$，对$n-1$求逆即可求出$key$

k=(str.index(i)*key+7)%37

str.index(i) = (k-7)*inverse(key,37) % 37

如果威尔逊定理不会用，可以选择爆破$key$，因为全部运算都在模37的域下进行，所以$key=(n-1)!\%key$在0-36的范围上，一个个爆破就行

n = 176778040837484895481963794918312894811914463587783883976856801676290821243853364789418908640505211936881707629753845875997805883248035576046706978993073043757445726165605877196383212378074705385178610178824713153854530726380795438083708575716562524587045312909657881223522830729052758566504582290081411626333
c = 'u66hp7nuh01puoaip10pi6o0vzavnu11'
str = 'abcdefghijklmnopqrstuvwxyz0123456789+='
key = inverse(n-1,n)
inv_key = inverse(key, 37)
m = ''
for i in c:
    m += str[((str.index(i) - 7) * inv_key % 37)]
print(m)

rssssssa

Coppersmith攻击，已知低位p，很常见的题，但是低位p的位数不足p的一半（但也相差不远），可以爆破几位p来增加已知低位p的位数（比赛的时候代码写错了，没出，很遗憾）

from Crypto.Util.number import *
import tqdm
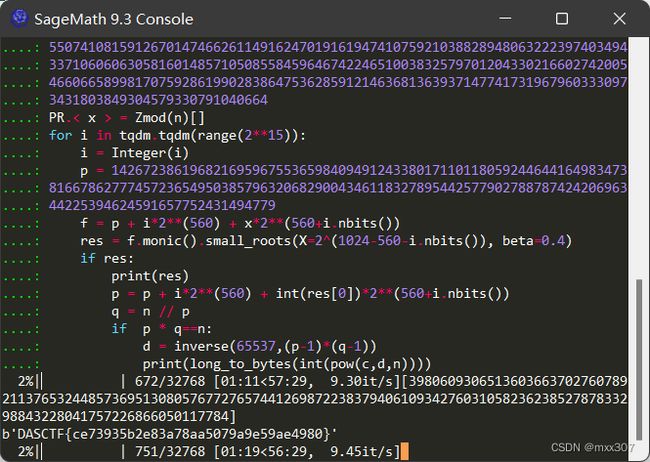
n = 21595945409392994055049935446570173194131443801801845658035469673666023560594683551197545038999238700810747167248724184844583697034436158042499504967916978621608536213230969406811902366916932032050583747070735750876593573387957847683066895725722366706359818941065483471589153682177234707645138490589285500875222568286916243861325846262164331536570517513524474322519145470883352586121892275861245291051589531534179640139953079522307426687782419075644619898733819937782418589025945603603989100805716550707637938272890461563518245458692411433603442554397633470070254229240718705126327921819662662201896576503865953330533
c = 1500765718465847687738186396037558689777598727005427859690647229619648539776087318379834790898189767401195002186003548094137654979353798325221367220839665289140547664641612525534203652911807047718681392766077895625388064095459224402032253429115181543725938853591119977152518616563668740574496233135226296439754690903570240135657268737729815911404733486976376064060345507410815912670147466261149162470191619474107592103882894806322239740349433710606063058160148571050855845964674224651003832579701204330216602742005466066589981707592861990283864753628591214636813639371477417319679603330973431803849304579330791040664
PR.< x > = Zmod(n)[]
for i in tqdm.tqdm(range(2**15)):
    i = Integer(i)
    p = 1426723861968216959675536598409491243380171101180592446441649834738166786277745723654950385796320682900434611832789544257790278878742420696344225394624591657752431494779
    f = p + i*2**(560) + x*2**(560+i.nbits())
    res = f.monic().small_roots(X=2^(1024-560-i.nbits()), beta=0.4)
    if res:
        print(res)
        p = p + i*2**(560) + int(res[0])*2**(560+i.nbits())
        q = n // p
        if  p * q==n:
            d = inverse(65537,(p-1)*(q-1))
            print(long_to_bytes(int(pow(c,d,n))))
# b'DASCTF{ce73935b2e83a78aa5079a9e59ae4980}'

normalNTRU

去年省赛easyNTRU，今年省赛normalNTRU，希望明年hardNTRU

确实是很正常的normalNTRU，不过没算出来，卡在了恢复m。虽然la博客上好像都有（博客ctrl+s到了本地），但是第一次验证的没成功，所以后面就放弃了博客上的求法，自己根据原理用题目给的函数恢复m，但没恢复出来~~，原因未知~~，少了一步中心提升(centerlift)，使域范围从[0,q)变换到(-q/2,q/2)。赛后再次按照博客上的方法时，又很神奇的行了，血亏

构造下图格，恢复$（f,g）$，根据解密算法恢复$m$

格密码 | Lazzaro (lazzzaro.github.io)

# 根据博客
from Crypto.Util.number import *
from Crypto.Hash import SHA3_256
from Crypto.Cipher import AES

def liftMod(f, q):
    g = list(((f[i] + q//2) % q) - q//2 for i in range(N))
    return R(g)

R.< x > = ZZ[]
c = b"\x90\xd4D\xd0\x0e\x19\x04\xd2]\xd5k\x0c&\xeas\xf42T\x89\x02\x10\xa7\x1b\x04aR|<,\xa8J/\x86\xdf@wW&\xf3\x1c}\x0e\xe1\xa4\xc4'\xffw\xc8\xcaT+\x10\xacR\xc0N\x99\x83\x1d}F\x0f\x99"
N = 66
p = 3
q = 2^20
hx = 847417*x^65 + 149493*x^64 + 671215*x^63 + 940073*x^62 + 422433*x^61 + 906071*x^60 + 661777*x^59 + 213093*x^58 + 776476*x^57 + 308727*x^56 + 199931*x^55 + 256166*x^54 + 201216*x^53 + 964303*x^52 + 961341*x^51 + 216401*x^50 + 503421*x^49 + 391011*x^48 + 724233*x^47 + 834103*x^46 + 534483*x^45 + 145755*x^44 + 31514*x^43 + 633909*x^42 + 611687*x^41 + 656421*x^40 + 51098*x^39 + 23193*x^38 + 874589*x^37 + 481483*x^36 + 772432*x^35 + 596655*x^34 + 924673*x^33 + 790137*x^32 + 711581*x^31 + 795565*x^30 + 179559*x^29 + 974401*x^28 + 252177*x^27 + 712781*x^26 + 292518*x^25 + 556867*x^24 + 247625*x^23 + 131231*x^22 + 545208*x^21 + 774544*x^20 + 810813*x^19 + 997461*x^18 + 951783*x^17 + 778973*x^16 + 225243*x^15 + 241753*x^14 + 419437*x^13 + 1013119*x^12 + 847743*x^11 + 60647*x^10 + 477291*x^9 + 674781*x^8 + 245115*x^7 + 745149*x^6 + 280553*x^5 + 298381*x^4 + 849205*x^3 + 541486*x^2 + 720005*x + 21659
ex = -34408*x^65 - 271875*x^64 - 72324*x^63 - 146782*x^62 - 191501*x^61 + 228014*x^60 - 236704*x^59 - 162996*x^58 - 93476*x^57 + 438756*x^56 - 340498*x^55 - 177073*x^54 + 309787*x^53 + 287611*x^52 - 13370*x^51 - 189635*x^50 + 271391*x^49 + 215846*x^48 - 286021*x^47 + 215770*x^46 + 259901*x^45 - 9022*x^44 - 410163*x^43 + 187965*x^42 - 99716*x^41 + 150105*x^40 + 161841*x^39 - 24872*x^38 - 288722*x^37 + 263847*x^36 + 142479*x^35 - 355131*x^34 - 181543*x^33 - 379836*x^32 + 206610*x^31 - 264717*x^30 - 381231*x^29 + 346552*x^28 - 59454*x^27 - 38411*x^26 - 200819*x^25 + 271459*x^24 + 169671*x^23 - 494515*x^22 - 250245*x^21 + 28462*x^20 + 485002*x^19 - 252744*x^18 + 301433*x^17 + 116488*x^16 - 359247*x^15 + 472604*x^14 + 16539*x^13 - 207870*x^12 - 137611*x^11 - 379327*x^10 + 477482*x^9 + 447007*x^8 - 368776*x^7 - 488265*x^6 - 312305*x^5 - 17292*x^4 + 372405*x^3 + 288980*x^2 + 95015*x - 99099
hn = [int(x) for x in hx.coefficients()]
n = len(hn)
A1 = matrix.identity(n)
A0 = matrix.zero(n)
Aq = matrix.identity(n) * q
Ah = matrix(ZZ, [hn[-i:] + hn[:-i] for i in range(n)])
M = block_matrix([A1,Ah,A0,Aq],nrows=2)
L = M.LLL()
v = L[2] # L[2:66]都行
f = list(v)[:n]
g = list(v)[n:]
f = R(f)
g = R(g)
assert hx == h
Q.< x > = Zmod(q)[]
P.< y > = Zmod(p)[]
qq = x ^ N - 1
pp = y ^ N - 1
fx = Q(f)
fy = P(f)
Fpy = fy.inverse_mod(pp)
ax = (fx * ex).mod(qq)
an = [int(x) for x in ax.coefficients()]
# 中心提升(centerlift)，使域范围从[0,q)变换到(-q/2,q/2)
for i in range(len(an)):
    if an[i] > q // 2:
        an[i] -= q
ax = P(an)
out = (Fpy * ax).mod(pp)
mm = liftMod(out, p)
mm = liftMod(mm, p)
sha3 = SHA3_256.new()
sha3.update(bytes(str(mm).encode('utf-8')))
key = sha3.digest()
cypher = AES.new(key, AES.MODE_ECB)
flag = cypher.decrypt(c)
print(flag)
# b'DASCTF{c4d2a7a2-1b1d-4ccb-95e6-655313e5a416}'

# 用题目给的函数解
from Crypto.Util.number import *
from Crypto.Hash import SHA3_256
from Crypto.Cipher import AES


def invertModPrime(f, p):
    Rp = R.change_ring(Integers(p)).quotient(x^N-1)
    return R(lift(1 / Rp(f)))

def convolution(f, g):
    return (f*g) % (x^N-1)

def liftMod(f, q):
    g = list(((f[i] + q//2) % q) - q//2 for i in range(N))
    return R(g)

def polyMod(f, q):
    g = [f[i]%q for i in range(N)]
    return R(g)

def invertModPow2(f, q):
    assert q.is_power_of(2)
    g = invertModPrime(f,2)
    while True:
        r = liftMod(convolution(g,f),q)
        if r == 1: return g
        g = liftMod(convolution(g,2 - r),q)

R.< x > = ZZ[]
c = b"\x90\xd4D\xd0\x0e\x19\x04\xd2]\xd5k\x0c&\xeas\xf42T\x89\x02\x10\xa7\x1b\x04aR|<,\xa8J/\x86\xdf@wW&\xf3\x1c}\x0e\xe1\xa4\xc4'\xffw\xc8\xcaT+\x10\xacR\xc0N\x99\x83\x1d}F\x0f\x99"
N = 66
p = 3
q = 2^20
hx = 847417*x^65 + 149493*x^64 + 671215*x^63 + 940073*x^62 + 422433*x^61 + 906071*x^60 + 661777*x^59 + 213093*x^58 + 776476*x^57 + 308727*x^56 + 199931*x^55 + 256166*x^54 + 201216*x^53 + 964303*x^52 + 961341*x^51 + 216401*x^50 + 503421*x^49 + 391011*x^48 + 724233*x^47 + 834103*x^46 + 534483*x^45 + 145755*x^44 + 31514*x^43 + 633909*x^42 + 611687*x^41 + 656421*x^40 + 51098*x^39 + 23193*x^38 + 874589*x^37 + 481483*x^36 + 772432*x^35 + 596655*x^34 + 924673*x^33 + 790137*x^32 + 711581*x^31 + 795565*x^30 + 179559*x^29 + 974401*x^28 + 252177*x^27 + 712781*x^26 + 292518*x^25 + 556867*x^24 + 247625*x^23 + 131231*x^22 + 545208*x^21 + 774544*x^20 + 810813*x^19 + 997461*x^18 + 951783*x^17 + 778973*x^16 + 225243*x^15 + 241753*x^14 + 419437*x^13 + 1013119*x^12 + 847743*x^11 + 60647*x^10 + 477291*x^9 + 674781*x^8 + 245115*x^7 + 745149*x^6 + 280553*x^5 + 298381*x^4 + 849205*x^3 + 541486*x^2 + 720005*x + 21659
ex = -34408*x^65 - 271875*x^64 - 72324*x^63 - 146782*x^62 - 191501*x^61 + 228014*x^60 - 236704*x^59 - 162996*x^58 - 93476*x^57 + 438756*x^56 - 340498*x^55 - 177073*x^54 + 309787*x^53 + 287611*x^52 - 13370*x^51 - 189635*x^50 + 271391*x^49 + 215846*x^48 - 286021*x^47 + 215770*x^46 + 259901*x^45 - 9022*x^44 - 410163*x^43 + 187965*x^42 - 99716*x^41 + 150105*x^40 + 161841*x^39 - 24872*x^38 - 288722*x^37 + 263847*x^36 + 142479*x^35 - 355131*x^34 - 181543*x^33 - 379836*x^32 + 206610*x^31 - 264717*x^30 - 381231*x^29 + 346552*x^28 - 59454*x^27 - 38411*x^26 - 200819*x^25 + 271459*x^24 + 169671*x^23 - 494515*x^22 - 250245*x^21 + 28462*x^20 + 485002*x^19 - 252744*x^18 + 301433*x^17 + 116488*x^16 - 359247*x^15 + 472604*x^14 + 16539*x^13 - 207870*x^12 - 137611*x^11 - 379327*x^10 + 477482*x^9 + 447007*x^8 - 368776*x^7 - 488265*x^6 - 312305*x^5 - 17292*x^4 + 372405*x^3 + 288980*x^2 + 95015*x - 99099
hn = [int(x) for x in hx.coefficients()]
n = len(hn)
A1 = matrix.identity(n)
A0 = matrix.zero(n)
Aq = matrix.identity(n) * q
Ah = matrix(ZZ, [hn[-i:] + hn[:-i] for i in range(n)])
M = block_matrix([A1,Ah,A0,Aq],nrows=2)
L = M.LLL()
v = L[2]
f = list(v)[:n]
g = list(v)[n:]
f = R(f)
g = R(g)
Fp = polyMod(invertModPrime(f, p), p)
Fq = polyMod(invertModPow2(f, q), q)
a = polyMod(convolution(ex,polyMod(f,q)),q)
an = [int(x) for x in a.coefficients()]
# 中心提升(centerlift)，使域范围从[0,q)变换到(-q/2,q/2)
for i in range(len(an)):
    if an[i] > q // 2:
        an[i] -= q
b = polyMod(an, p) # 不能直接b = polyMod(a, p)
m = polyMod(convolution(Fp,b),p)
m = liftMod(m,p)
sha3 = SHA3_256.new()
sha3.update(bytes(str(m).encode('utf-8')))
key = sha3.digest()
cypher = AES.new(key, AES.MODE_ECB)
flag = cypher.decrypt(c)
print(flag)
Fp,b),p)
m = liftMod(m,p)
sha3 = SHA3_256.new()
sha3.update(bytes(str(m).encode('utf-8')))
key = sha3.digest()
cypher = AES.new(key, AES.MODE_ECB)
flag = cypher.decrypt(c)
print(flag)

总结

我是废物，比赛只出了一题，拖了后腿，痛失一等，给队友磕个头吧