高等代数 线性映射(第9章)2 线性映射的矩阵表示,特征值与特征向量,对角化

一.线性映射的矩阵表示(9.3)
1.线性映射的矩阵表示
(1)概念:



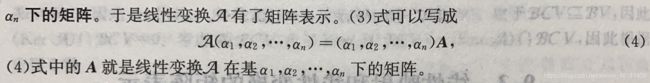
(2)线性变换的矩阵的维数:

命题1:设$Ꭿ$是域$F$上$n$维线性空间$V$上的线性变换,它在$V$的1个基${\alpha }_1...{\alpha }_n$下的矩阵为$A$,则$$rank(Ꭿ)=rank(A)(9)$$

2.$Hom(V,V^{\prime })$与$M_{s\times n}(F)$的关系
(1)作为线性空间的同构关系:

定理1:设$V,V^{\prime }$分别是域$F$上的$n,s$维线性空间,则$V$到$V^{\prime }$的线性映射$Ꭿ$与其在$V$的1个基和$V^{\prime }$的1个基下的矩阵$A$的对应是线性空间$Hom(V,V^{\prime })$到$M_{s\times n}(F)$的1个同构映射,从而$$\begin{gathered} Hom(V,V^{\prime })\cong M_{s\times n}(F)(12) \\ dim(Hom(V,V^{\prime }))=sn=(dimV)(dim{V}^{\prime })(13) \end{gathered}$$特别地,有$$\begin{gathered} Hom(V,V)\cong M_n(F)(14) \\ dim(Hom(V,V))=n^2=(dimV{)}^2(15) \end{gathered}$$

(2)作为代数的同构关系:

定理2:设$V$是域$F$上的$n$维线性空间,$V$上的线性变换$Ꭿ$与其在$V$的1个基下的矩阵$A$的对应是代数$Hom(V,V)$到代数$M_n(F)$的1个同构映射,从而代数$Hom(V,V)$与代数$M_n(F)$是同构的

注:从上述推导过程看出$$\begin{gathered} Ꭿ[({\alpha }_1...{\alpha }_n)B]=(Ꭿ{\alpha }_1...Ꭿ{\alpha }_n)B \\ =[Ꭿ({\alpha }_1...{\alpha }_n)]B(17) \end{gathered}$$并且当$B$是$n\times m$矩阵时,(17)式仍成立

3.向量在线性映射下的象的坐标:


4.线性变换在不同基下的矩阵间的关系
(1)线性变换在不同基下的矩阵相似:

定理3:设$V$是域$F$上的$n$维线性空间,$V$上的1个线性变换$Ꭿ$在基${\alpha }_1...{\alpha }_n$下的矩阵为$A$,在基${\eta }_1...{\eta }_s$下的矩阵为$B$,从基${\alpha }_1...{\alpha }_n$到基${\eta }_1...{\eta }_s$的过渡矩阵为$S^{①}$,则$$B=S^{-1}AS(22)$$

注:①易证明基到基的过渡矩阵$S$一定可逆:

(2)线性变换的行列式/迹/秩:


(3)相似标准型:

二.特征值与特征向量,可对角化的条件(9.4)

1.线性变换的特征值与特征向量
(1)概念:


(2)线性变换的特征值/特征向量与矩阵的特征值/特征向量:


2.线性变换可对角化的条件
(1)线性变换可对角化的概念:

(2)线性变换可对角化的条件:

定理4:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当$Ꭿ$有$n$个线性无关的特征向量${\xi }_1...{\xi }_n$,此时$Ꭿ$在基${\xi }_1...{\xi }_n$下的矩阵为$$\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right](4)$$其中${\lambda }_i$是${\xi }_i$所属的特征值(即$Ꭿ{\xi }_i={\lambda }_i{\xi }_i$),$i=1,2...n$;矩阵(4)称为$Ꭿ$的标准型;除了主对角线上元素的排列次序外,$Ꭿ$的标准型是由$Ꭿ$唯一决定的

推论1:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当$V$中存在由$Ꭿ$的特征向量组成的1个基

(3)特征子空间:

注:①对线性变换$Ꭿ$的任意特征值${\lambda }_0$,必有零向量属于$V_{{\lambda }_0}$;即$V_{{\lambda }_0}=\{{\xi }_1,{\xi }_2...{\xi }_m,0\}$,其中${\xi }_i(i=1,2...n)$为属于${\lambda }_0$的所有特征向量,$0$为零向量

推论2:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当$Ꭿ$的属于不同特征值的特征子空间的维数之和等于$n$

推论3:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当$Ꭿ$的所有不同的特征值的特征子空间的基合起来是$V$的1个基

推论4:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当下式成立:$$V=V_{{\lambda }_1}\oplus V_{{\lambda }_2}\oplus ...\oplus V_{{\lambda }_s}(8)$$其中${\lambda }_1,{\lambda }_2...{\lambda }_s$是$Ꭿ$全部的不同的特征值

该推论是通过线性变换研究线性空间结构的体现

(4)特征多项式:

命题2:域$F$上$n$维线性空间$V$上的线性变换$Ꭿ$可对角化当且仅当$Ꭿ$的特征多项式在$F[\lambda ]$中可分解成$$(\lambda -{\lambda }_1{)}^{l_1}(\lambda -{\lambda }_2{)}^{l_2}...(\lambda -{\lambda }_s{)}^{l_s}(12)$$其中${\lambda }_1...{\lambda }_s$两两不等,且$Ꭿ$的每个特征值${\lambda }_i(i=1,2...s)$的几何重数等于其代数重数

附录.$n$个线性空间的笛卡儿积

设$V$是域$F$上的线性空间,则$n$个$V$的笛卡儿积为$$V^n:=\underset{n个}{V\times V\times ...\times V}:=\{({\alpha }_1,{\alpha }_2...{\alpha }_n)|a_i\in V,i=1,2...n\}$$规定$({\alpha }_1,{\alpha }_2...{\alpha }_n)=({\beta }_1,{\beta }_2...{\beta }_n)\iff {\alpha }_i={\beta }_i(i=1,2...n)$
定义加法运算:若$({\alpha }_1,{\alpha }_2...{\alpha }_n),({\beta }_1,{\beta }_2...{\beta }_n)\in V^n$,则$$({\alpha }_1,{\alpha }_2...{\alpha }_n)+({\beta }_1,{\beta }_2...{\beta }_n):=({\alpha }_1+{\beta }_n,{\alpha }_2+{\beta }_n...{\alpha }_n+{\beta }_n)$$
定义纯量乘法运算:若$({\alpha }_1,{\alpha }_2...{\alpha }_n)\in V^n,k\in F$,则$$k({\alpha }_1,{\alpha }_2...{\alpha }_n):=(k{\alpha }_1,k{\alpha }_2...k{\alpha }_n)$$
易证明$V^n$为域$F$上的线性空间
定义$V^n$中元素与域$F$上的矩阵$A,B$的乘法(相当于按列分块的矩阵与普通矩阵的乘法):$$\begin{gathered} \left[\begin{array}{ccc}{\alpha }_1& ...& {\alpha }_n\end{array}\right]\left[\begin{array}{ccc}{a}_{11}& ...& a_{1m}\\ ...& ...& ...\\ a_{n1}& ...& a_{nm}\end{array}\right] \\ =(a_{11}{\alpha }_1+...+a_{n1}{\alpha }_n,a_{12}{\alpha }_1+...+a_{n2}{\alpha }_n...a_{1m}{\alpha }_1+...+a_{nm}{\alpha }_n)\in V^m \end{gathered}$$该运算满足以下运算法则:
①$[({\alpha }_1,{\alpha }_2...{\alpha }_n)A]B=({\alpha }_1,{\alpha }_2...{\alpha }_n)(AB)$
②$k[({\alpha }_1,{\alpha }_2...{\alpha }_n)A]=[k({\alpha }_1,{\alpha }_2...{\alpha }_n)]A=({\alpha }_1,{\alpha }_2...{\alpha }_n)(kA)$