算法day20|654,617,700,98
654. Maximum Binary Tree
我的代码:但是出错了,但是大概的思路是对的!得出结论,终止条件设置错误,if nums 为0
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
#设置最大根节点
if root is None:
return None
root_val = max(nums)
root_index = nums.index(root_val)
root = TreeNode(root_val)
#找左边区间
left_intervel = nums[:root_index]
#找右边区间
right_intervel = nums[root_index+1:]
#左节点,找下一个大的
root.left = self.constructMaximumBinaryTree(left_intervel)
#右节点,找
root.right = self.constructMaximumBinaryTree(right_intervel)
return root构造二叉树系列的题目,需要使用前序遍历来构造二叉树。
什么时候要在左右遍历那个地方写if语句?需要根据终止条件来判断,
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
#终止条件
if not nums:
return None
#中
#存入最大值
max_val = max(nums)
max_index = nums.index(max_val)
root = TreeNode(max_val)
#左节点,找下一个大的
#找左边区间
left_interval = nums[:max_index]
root.left = self.constructMaximumBinaryTree(left_interval)
#右节点
#找右边区间
right_interval = nums[max_index+1:]
root.right = self.constructMaximumBinaryTree(right_interval)
#返回值
return root
617. Merge Two Binary Trees
合并二叉树
合并到第一棵树上
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
#终止条件,当节点为空的时候,返回所对应的另一个树的值.因为他们是同步遍历的
if root1 is None: return root2
if root2 is None: return root1
#中序遍历
root1.val += root2.val
#左
root1.left = self.mergeTrees(root1.left,root2.left)
#右
root1.right = self.mergeTrees(root1.right,root2.right)
#返回值,我们将二叉树合并到第一个树
return root1合并到 新的树上
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
#终止条件,当节点为空的时候,返回所对应的另一个树的值.因为他们是同步遍历的
if root1 is None: return root2
if root2 is None: return root1
#中序遍历
#创建新的树
newtree = TreeNode(0)
newtree.val = root1.val + root2.val
#左
newtree.left = self.mergeTrees(root1.left,root2.left)
#右
newtree.right = self.mergeTrees(root1.right,root2.right)
#返回值,我们将二叉树合并到第一个树
return newtree700. Search in a Binary Search Tree
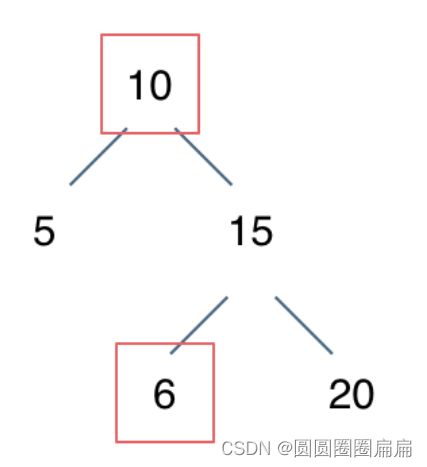
 二叉搜索树的特征: 根节点比左子树的所有值都大, 比右子树的所有值都小
二叉搜索树的特征: 根节点比左子树的所有值都大, 比右子树的所有值都小
递归法:
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
#终止条件 当根节点为空,返回root,或者当根节点的值为val的值
if root is None or root.val == val:return root
#创建一个节点,接住返回的指针.左子树如果搜索到了val,要将该节点返回。 如果不用一个变量将其接住,那么返回值不就没了。
result = TreeNode()
#如果val的值比根的大,往右(二叉搜索的特性)
if val>root.val:
result = self.searchBST(root.right,val)
if val < root.val:
result = self.searchBST(root.left,val)
return result 迭代法:
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
#迭代法
while root:
if val > root.val:
root = root.right
elif val98. Validate Binary Search Tree
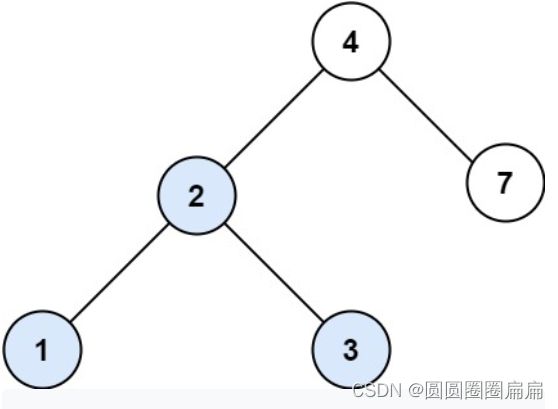
需要去验证二叉搜索树,如果遍历完,元素都是递增的,那么就是二叉搜索树
如果是空节点 是不是二叉搜索树呢?是的,二叉搜索树也可以为空
第一种想法:
递归二叉树,将值保存到数组中,如果数组是单调递增的,那么就是二叉搜索树
第二种:
递归二叉树,直接遍历二叉树是不是单调递增
def isValidBST(self, root: TreeNode) -> bool:
cur_max = -float("INF")
def _isValidBST(root: TreeNode) -> bool:
nonlocal cur_max
#终止条件
if not root:return True
#左
left = _isValidBST(root.left)
#中
if root.val> cur_max:
cur_max = root.val
else:
return False
#右
right = _isValidBST(root.right)
#如果左子树满足条件,右子树也满足条件
return left and right
return _isValidBST(root)代码误区:(我就是那么做的)
if (root.left is not None) and (root.right is not None) and (root.val > root.left.val) and (root.val < root.right.val): return True判断根节点是不是比左节点大,比右节点小。很容易陷入误区。因为根节点需要比左子树的所有值都小。要比右子树所有值都大。
第三种:
递归二叉树,直接遍历二叉树是不是单调递增,这里使用指针优化
Non-local的使用:
count = 1
def a():
count = 'a函数里面' #如果不事先声明,那么函数b中的nonlocal就会报错
def b():
nonlocal count
print(count)
count = 2
b()
print(count)
if __name__ == '__main__':
a()
print(count)下面会报错:
count = 1
def a():
#nonlocal count #这种声明方法肯定报错,
def b():
nonlocal count #在a()函数中没有提前声明,所以报错
print(count)
count = 2
b()
print(count)
if __name__ == '__main__':
a()
print(count)
Python3 中的nonlocal用法 - 希望中追寻 - 博客园
定义负无穷怎么定义:
cur = -float("INF")