离线强化学习论文学习 Critic Regularized Regression

Critic Regularized Regression

1.摘要

离线强化学习(RL)，也被称为批量RL，提供了在没有在线环境交互的情况下从大型预记录数据集进行策略优化的前景。它解决了数据收集成本和安全性方面的挑战，这两方面都与RL的实际应用特别相关。

不幸的是，大多数非策略算法在从固定数据集学习时表现很差。在本文中，我们提出了一种新的离线RL算法，使用一种形式的临界正则化回归(CRR)从数据中学习策略。我们发现，CRR的表现惊人地好，可扩展到具有高维状态和动作空间的任务——在广泛的基准任务中，它的表现大大超过了几种最先进的离线RL算法。

2.Introduction

深度强化学习(RL)算法在许多具有挑战性的领域取得了成功。

然而，这些领域很少涉及现实世界的决策制定。一个重要的原因是，在学习过程中在线执行政策，我们称之为在线RL，由于成本、安全和伦理[8]的原因，往往不可行或不可取。在医疗保健、工业控制和机器人领域显然就是如此。然而，对于其中的许多领域，可以获得大量的历史数据。这再次引起了人们对离线RL方法(也称为批处理RL[19])的兴趣，这些方法旨在从日志数据中学习策略，而不需要与真实系统进行进一步的交互。

这种对离线RL的兴趣被RL中的评估危机进一步放大:RL涉及探索和经验学习之间的密切相互作用，这使得算法比较困难。通过将这两个问题解耦，专注于从固定的经验中学习，就有可能与基准共享数据集，以改善该领域的协作和评估。

最初的带有函数估计的离策略强化学习算法直接应用到离线强化学习的设定中通常会导致失败。一个共同的结论是，失败源于过度乐观的Q值估计值，以及对于数据不恰当的外推。与bootstrapping结合使用时，问题尤其严重，因为在bootstrapping中，q函数会查询未被观察到的动作，并且会积累错误。

在本文中，我们提出了一种新的离线RL算法，使用一种形式的临界正则化回归(CRR)从数据中学习策略。CRR本质上将离线策略优化简化为一种值过滤回归，这种回归只需要对标准参与者-批评者方法进行最小的算法更改。因此，它很容易理解和实现。图1直观地解释了CRR。

尽管CRR看起来很简单，但我们的实验表明，在广泛的基准测试任务中，它的性能明显优于几种最先进的离线RL算法。此外，非常重要的是，它可以扩展到具有高维状态和行动空间的任务，并且可以很好地处理各种或低质量数据集。

3.Related Work

对于离线RL的全面深入的评论，我们推荐读者阅读Lange等人[19]和Levine等人[20]。后者提供了该领域最近的广泛评价。

行为克隆(BC)是最简单的离线学习形式。从状态-操作对的数据集开始，训练策略通过监督损失将状态映射到操作。当数据集包含高质量的数据时，这种方法可能会非常有效，例如由专家为感兴趣的任务生成轨迹。然而，它很容易失败(i)当数据集包含大量随机或与任务无关的行为;或者(ii)当学习到的策略诱导了一个远离考虑的数据集的轨迹分布。

非策略深度RL算法提供了BC的替代方案。与BC不同，这些方法可以利用奖励函数来超越演示者，参见Cabi et al[6]。最近，研究表明，分布式非策略深度RL技术[5,4]与非分布式技术不同，它在Atari[2]和机器人操作[6]中的离线RL中工作得很好。Fujimoto等人最近的一篇论文[9]证实了分布变量本身可以更有效，但与专门为离线RL设计的算法(称为批约束深度q学习(BCQ)[10])相比，性能不佳。

已经提出了几种方法来克服离线设置中非策略深度RL的问题。这些失败大多归因于不恰当的归纳和过于自信的Q估计。一项工作集中在约束行动选择以支持训练数据[10,17,31,15]。这可以通过首先学习数据的生成模型，然后从该模型中采样动作来实现Q-learning[10]。生成模型也可以用约束优化来约束估计的RL策略[17,15]。Fujimoto等人[10]和Kumar等人[17]进一步使用多个q函数估计来减少乐观偏见。

离线RL的第二种攻击方式是执行加权行为克隆。其思想是使用优势函数的估计值在数据集中为BC选择最佳操作。这在精神上与图1中提供的动机相似。这种方法的例子包括单调优势重加权模仿学习(MARWIL)[38]，最佳动作模仿学习(BAIL)[7]，优势加权行为模型(ABM)[31]和优势加权回归[28]，这些都是之前以具有低维策略类[27]的拟合q迭代算法的形式研究的。我们的方法与大多数方法的不同之处在于，我们不依赖观察到的收益来进行优势估计——如第3节所阐述的那样。此外，我们引入了一种称为“批评加权策略”(CWP)的技术，它使用学习到的批评来改进测试时的结果。

Nair等[26]提出了一种简单的(二进制)版本的CRR过滤组件，其结果表明，该过滤器只是加速了训练，但在长期范围内给出了混合的结果。在van Hasselt和Wiering[37]中可以找到一个类似算法的早期版本。需要注意的是，这些工作执行过滤BC，但在在线设置中，允许进一步收集数据，因此过滤可能发挥较小的作用。在线设置比离线设置要宽容得多，这是本文的重点。事实上，我们在第4节中的分析表明，在离线环境中，设计元素，如二进制和指数滤波的样本估计、使用CWP的策略改进、精心设计的深度循环网络以及分布值函数的使用，会对结果的质量产生显著影响。与我们的工作同时，[25]提出了优势加权Actor批评家(AWAR)，以加速离线数据集的在线RL。它们的形式等价于指数滤波的CRR。

4. 评论家正则化回归

我们推出了评论家正则化回归(CRR)，一个简单，但有效的离线RL方法。

4.1 策略评估

假设我们给定一个固定数据集B，其中包含单个转换元组(st, at, rt, st+1)或K步轨迹(st, at, rt, st+1, at+1，···，st+K)。为了简单起见，我们将只考虑第一种情况，但所有的算法发展都直接适用于k步轨迹。在许多off-policy学习方法中，一个重要的步骤是off-policy策略评估。这通常涉及到学习一个近似的Q函数最小化时序差分损失类似于下面：

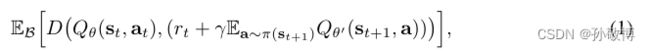
其中对数据的期望通过抽样(st, at, rt, st+1) ~ B获得，D是一些散度测度来近似;测量基于目标网络[24]的动作值Qθ(st, at)(对于策略π)的电流估计和td-更新之间的差异。我们注意到，我们使用了分布q函数，如在Barth-Maron等，而不是使用平方误差的D。

正如在最近的工作中所讨论的，[例如10,17,31]，如果没有环境交互(离线RL设置)，由于上述的“bootstrapping”问题，这种损失可能会有问题;其中，我们通过Ea ~ π(st+1)Qθ0(st+1, a)来评估下一个状态st+1的值。如果使用标准RL训练，参数π(·|st+1)可能会外推到训练数据之外，并提出b中不包含的动作。因为这些动作Q没有经过训练，可能会产生不好的估计。

4.2 通过CRR进行策略学习

为了缓解上述问题，我们希望避免对不属于B的(s, a)求Q值。因此，我们的目标是通过阻止π采取训练分布之外的行为来训练π。用标准的策略梯度很难实现这一要求。因此，我们改变了目标，以匹配训练数据中包含的状态-动作映射——但被q函数过滤了。具体来说,我们优化

其中f是一个非负标量函数，其值在Qθ范围内单调递增。从根本上说，式(2)试图复制数据中存在的动作，从而限制了π。学习目标的进一步属性可以通过对f的不同选择来控制，例如当f:= 1时，Eq.(2)相当于Behavioral Cloning (BC)。然而，BC的成功在很大程度上依赖于数据集B的质量。当B不包含执行良好的策略生成的足够多的转换时，或者糟糕数据的比例太大时，BC很可能会失败。

假设Q对于(s, a)∈B足够准确(例如，使用Eq.(1)学习)，我们可以考虑f的额外选择，使非策略学习能够克服这个问题:

其中β > 0为超参数，1为指标函数，ˆa θ(s, a)为优势估计函数。公式(2)与训练[31]之前行为的目标相似。更准确地说，通过使用公式(3)中的f和ˆAK(见表1)，我们恢复了ABM ’ priorpolicy '的形式。直观上，Eq.(3)在过滤后的数据集上包含BC，其中过滤增加了我们从中学习的动作的平均质量。过滤器是根据当前策略的值定义的。

指数加权作为正则化策略迭代。我们可以通过认识到Eq.(4)在策略迭代方案中近似地实现了一个正则化的策略改进步骤来深入了解它。

考虑

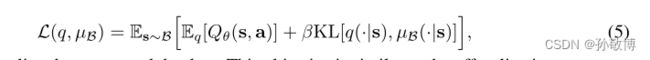
其中，“µB”为生成数据的策略。这个目标类似于MPO[1]的off-policy改进，但是使用的是µB而不是策略优先。实现此目标的最优策略为q(a|s) = exp(q θ(s,a)/β)µB(a|s)/Z(s)。Z(s)在我们的设置中很难评估(我们只能访问B)，所以我们在实践中使用q(a|s)∝exp(ˆa θ(s, a)/β)，从而通过减去V (s)执行隐式、近似的每个状态归一化。将这个分布投影到参数策略πφ上可以通过最小化跨熵H[q(·|s)， πφ(·|s)]来完成。再次，为了避免计算q的归一化常数，我们使用来自数据集B的样本来估计这个交叉熵，这产生了Eq.(2)与在Eq.(4)中选择f。最小化这个交叉熵对应于“磨尖”动作分布µB，给予更好的动作更高的权重。此外，当β→∞时，这个目标就变成了行为克隆(BC)。

表格设置中的理论分析。在附录中，我们展示了在表格设置中，CRR是安全的，因为它将操作选择限制在对数据的支持上，并且可以解释为实现了一种改进行为策略的策略迭代方案。

优势估计器的选择。由于我们对高维动作空间感兴趣，我们使用CRR(算法1)优势的样本估计。我们对比表1中ˆa的不同选择。从这些我们考虑ˆAmean，但发现对于小m它可能高估的优势，由于随机性。对于公式(3)中的f，这可能导致包含次优行动。因此，我们也考虑ˆAmax;对优势的悲观估计。

除了在FQI-AWR[27]上的工作——作者考虑了一个更简单的设置，使用简单的基于核的回归学习Q和V，然后基于优势加权的政策学习——最近的文献主要考虑了基于k步或蒙特卡洛返回的优势估计(ˆAK，ˆAM C在表中)。其中，我们在Eq.(3)和Eq.(4)中的公式类似于上面突出显示的[31]。它也与最近关于优势加权回归[38,28]的工作有一些相似之处，后者使用ˆAK或ˆAM C与学习到的V函数来形成优势估计。我们发现这个选择在许多离线RL场景中都不能很好地工作，我们将在下面解释。

我们的算法的完整列表在1;我们还采用了深度RL文献中的标准实践来稳定训练(例如目标网络)，并注意我们使用了分布批评。

CRR与基于回报的方法。当数据非常不符合政策时，使用K-step返回(K > 1)可能会有问题，我们将在附录中实验性地展示。此外，在随机环境中，使用K-step(或偶发性)回报来估计优势可能会导致冒险或其他不受欢迎的行为。为了说明这一点，让我们考虑以下简单的双臂强盗问题:第一个手臂产生的收益是0或1，各有50%的概率。第二条支路产生0.9的确定性收益，因此它应该是有利的支路。

让我们假设数据集中2/3的动作是拉动第一个手臂，剩下的1/3是拉动第二个手臂。一个完美学习的Q函数显然更倾向于臂二而不是臂一。通过使用收益R进行优势估计(计算优势为R - V)，然而，优势加权回归(AWR)[28]，或类似的方法，会更倾向于第一臂而不是第二臂;不考虑温度参数。同样，在ABM[31]中学习到的先验会平等地选择这两个动作，因此也会有不足。对于ABM，额外的RL步骤可能会恢复正确的操作选择(取决于允许RL策略与之前的策略偏离多远)，但不能保证它会恢复。最后但并非最不重要的是，依赖于奖励过滤的方法也会倾向于手臂1而不是手臂2。

批评加权政策(CWP)。学习到的q函数可以在策略执行过程中用于执行额外的近似策略改进步骤。事实上，基于搜索的方法已经在离散域[33]中利用了这一事实。我们可以考虑Eqn的解。(5)虽然现在使用学者政策πφ作为先验。给出的解决方案是¯q = arg max¯q L(¯q,πφ),该收益率¯q (|) = exp (qθ(s) /β)πφ(|)/ Z (s)。我们可以在动作选择期间使用这个策略而不是π。为了从¯q开始抽样，我们使用了重要性抽样。我们首先从πφ(·|s)中对作用a1:n进行采样，然后用它们的重要权重exp(Qθ(s,ai)/β)对不同作用进行加权，最后用概率P (ai) = exp(Qθ(s,ai)/β)/Pn j=1 exp(Qθ(s,aj)/β)重新采样选择作用。注意，这对应于自归一化的重要性抽样，不需要访问Z(s)

5. 总结
   5.1 策略估计
   策略估计方面，已知四元组(st, at, rt, st+1)，使用公式进行策略评估：
   
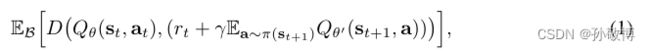
   其中(st, at, rt, st+1) 采样自数据集 B，D是度量函数，注意其中使用了分布Q函数，并没有使用平方差度量函数。
   问题： 在离线强化学习的数据集B中，使用在线强化学习算法会导致策略π(·|st+1)外推到数据集之外，并可能出现数据集B中没有的动作。而由于数据集不包含的动作的Q值并没有被训练过，因此可能会产生不好的估计。
   5.2 策略学习(使用CRR)
   为缓解上述问题，这里目标是尽量避免出现不在数据集中的(s, a)对。因此这里改变了目标函数如下：
   
   其中f为一个非负标量函数，其对于Q值单调递增。其试图复制数据集中存在的动作，因此可以限制策略。目标函数进一步可以通过对f 进行选择来改进，当f=1时目标函数等同于行为克隆。但BC算法很依赖于好的数据。
   5.3 f选择
   对于足够准确的(s, a)∈B，可以考虑f的额外选择，使off-policy算法克服这个问题:
   
   其中β > 0为超参数，1为指标函数，ˆAθ(s, a)为优势估计函数。
   5.4 公式分析
   公式4近似地实现了正则化策略。
   (1) 目标函数如下：（希望Q大，KL散度小）
   
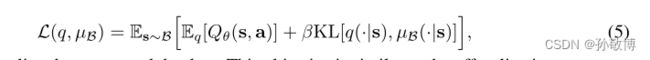
   其中µB为生成数据的策略
   (2) 实现此目标的最优策略为：（这里还不太理解）
   
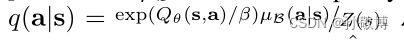
   (3) 但Z(s)很难评估，所以在实践中使用：
   
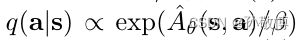
   从而通过减去V (s)执行隐式、近似的每个状态归一化。
   (4) 为了将这个分布投影到参数策略πφ上，最小化交叉熵
   
   (5) 为了避免计算Q的归一化常数，我们使用来自数据集B的样本来估计这个交叉熵。这等价于
   
   f使用：
   
   最小化这个交叉熵对应于“磨尖”动作分布µB，给予更好的动作更高的权重。此外，当β→∞时，这个目标就变成了行为克隆(BC)。
   5.5 优势函数估计
   由于对高维动作空间感兴趣，我们使用CRR优势的样本估计。对比了表中不同优势函数选择。这里考虑了Amean，但由于随机性会出现价值高估现象。对于公式(3)中的f可能导致次优策略。因此，也考虑Amax对优势函数的悲观估计。
   使用K步优势加权来形成优势估计在许多离线RL场景中都不能很好地工作。CRR与基于回报的方法。当数据非常不符合政策时，使用K-step返回(K > 1)可能会有问题。此外，在随机环境中，使用K-step(或偶发性)回报来估计优势可能会导致冒险或其他不受欢迎的行为。
   
   所以第二个相对更优。
   5.6 批评加权政策(CWP)
   学习到的q函数可以在策略执行过程中用于执行额外的近似策略改进步骤。为了从¯q抽样，这里使用了重要性抽样。首先从πφ(·|s)中对动作a1:n进行采样，然后用它们的重要权重exp(Qθ(s,ai)/β)
   对不同动作进行加权，最后用概率
   
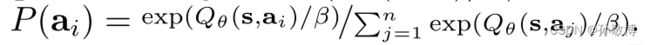
   进行动作选择。注意，这对应于自归一化的重要性抽样，不需要访问Z(s)。