深度学习之激活函数详解及实现
激活函数就相当于神经元的开关一样,在分类任务中,通过激活函数打开不同的神经元来表示属于哪一类。
1 经典的激活函数
经典激活函数有下面几种:
- sigmoid
- tanh
- ReLu
- Leaky ReLu
- ELU(Exponential Linear Units)
sigmoid是第一代取代阶梯函数的激活函数,从科学的角度,它确实能够实现对神经元的激活和非激活,从而实现不同的表示,当初它的使用场景是二分类,不过现在使用也是二分类,在很多场景基本上不使用它。由于它是在0-1之间,在训练初期是收敛速度很慢,所以提出tanh,它是介于-1和1之间,它的输出是以0为中心,有助于初期训练的收敛,但是sigmoid和tanh都是饱和函数,也就是在当输入很大或者很小时,出现梯度会很小,出现梯度消失的现象,学习会非常慢,这就是梯度消失的问题。因此出现了Relu,它是非饱和函数,从公式可以看出,其计算简单,所以速度快,其斜率是个常数,所以不会出现梯度消失的问题,也是目前比较常用的激活函数。但是它也有个致命的缺点,就是任何负数计算的最终结果都是0,这样就会出现很多神经元是0,神经元不会被激活,死掉了,所以又称它为死亡ReLu,一旦神经元死掉,影响其表示能力,针对这个问题,对ReLu进行升级,提供了Leak ReLu,在负数的情况给一个很小的斜率,保障负数的梯度不是0,保障神经元不死。最后ELU激活函数出现,击败了Leak ReLu,它将tanh,Leak ReLu的所有缺点都规避了,同时还有一个优点,就是它在0处是平滑的,加速了网络的收敛,但是其计算速度相对较慢,主要是因为其指数函数。
简单的总结下:
- sigmoid 函数:除了输出层是一个二分类问题,基本不会使用它。
- tanh 函数,tanh 是非常优秀的,几乎适合所有的场景
- ReLu 激活函数,最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者Leaky ReLu。
2 经典的激活函数及Numpy实现
上面已经说了,经典激活函数的演变以及优点和缺点,下面我们来看看具体公式和代码实现。
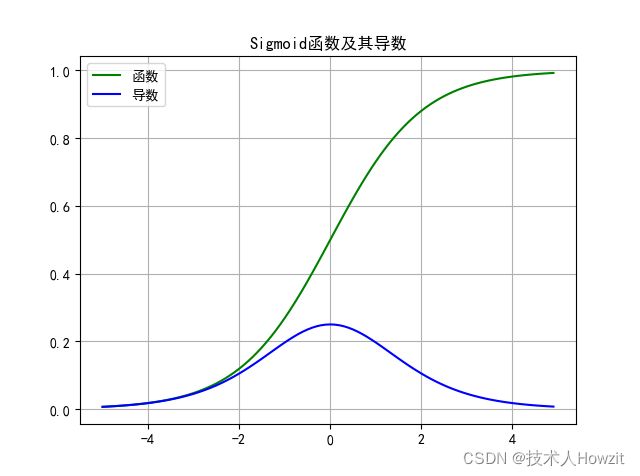
2.1 sigmoid
- 公式:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
- 导数: f ( x ) ′ = f ( x ) ( 1 − f ( x ) ) f(x)'=f(x)(1-f(x)) f(x)′=f(x)(1−f(x))
- 代码实现:
class Sigmoid:
def __call__(self, x):
return 1 / (1 + np.exp(-x))
def gradient(self, x):
return self.__call__(x) * (1 - self.__call__(x))
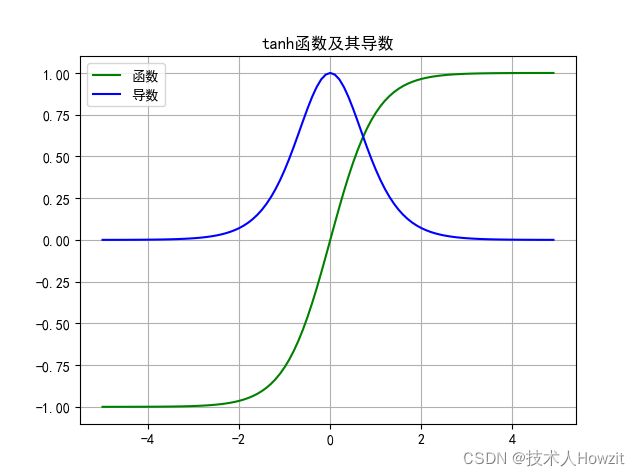
2.2 tanh
- 公式: f ( x ) = e x − e − x e x + e − x = s i n h ( x ) c o s h ( x ) f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{sinh(x)}{cosh(x)} f(x)=ex+e−xex−e−x=cosh(x)sinh(x)
- 导数: f ( x ) ′ = ( 1 − f ( x 2 ) ) f(x)'=(1-f(x^2)) f(x)′=(1−f(x2))
- 代码实现:
class Tanh:
def __call__(self, x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def gradient(self, x):
return 1 - np.square(self.__call__(x))
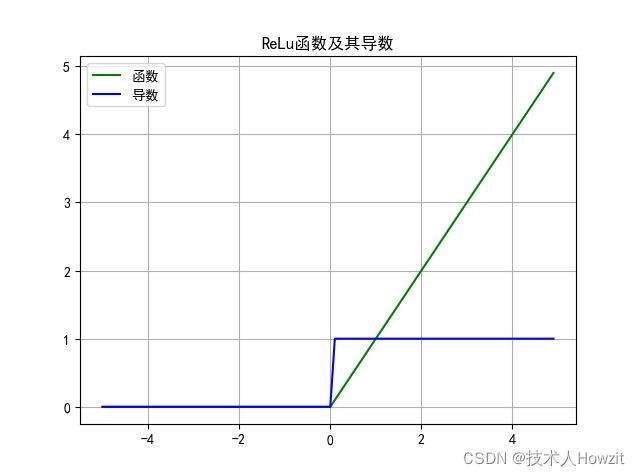
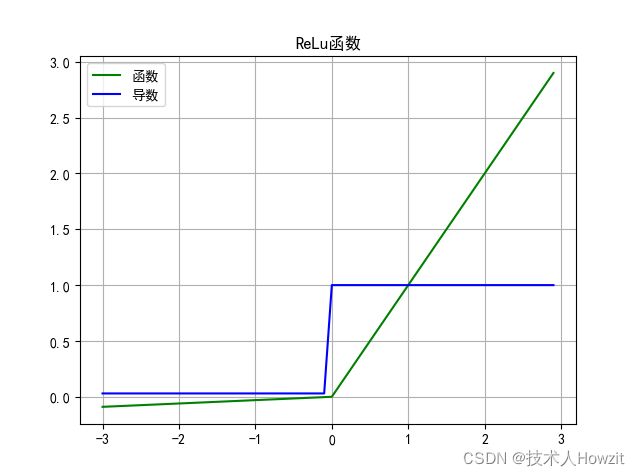
2.3 ReLu
- 公式: r e l u ( x ) = { x i f x > 0 0 i f x ≤ 0 relu(x)=\begin{cases}x\quad if \quad x>0\\{0\quad if\quad x\leq0}\end{cases} relu(x)={xifx>00ifx≤0
- 导数: r e l u ( x ) ′ = { 1 i f x > 0 0 i f x ≤ 0 relu(x)'=\begin{cases}1\quad if \quad x>0\\{0\quad if\quad x\leq0}\end{cases} relu(x)′={1ifx>00ifx≤0
- 代码实现:
class ReLu:
def __call__(self, x):
return np.where(x > 0, x, 0)
def gradient(self, x):
return np.where(x > 0, 1, 0)
2.4 Leak ReLu
- 公式: f ( x ) = { x i f x > 0 x ∗ α i f x < = 0 f(x)=\begin{cases}{x \quad if \quad x>0}\\{x*\alpha \quad if \quad x<=0}\end{cases} f(x)={xifx>0x∗αifx<=0
- 导数: f ( x ) = { 1 i f x > 0 α i f x < = 0 f(x)=\begin{cases}{1 \quad if \quad x>0}\\{\alpha \quad if \quad x<=0}\end{cases} f(x)={1ifx>0αifx<=0
- 实现:
class LeakReLu:
def __init__(self, alpha=0.03):
self.alpha = alpha
def __call__(self, x):
return np.where(x > 0, x, self.alpha * x)
def gradient(self, x):
return np.where(x > 0, 1, self.alpha)
def __str__(self):
return "Leak ReLu"
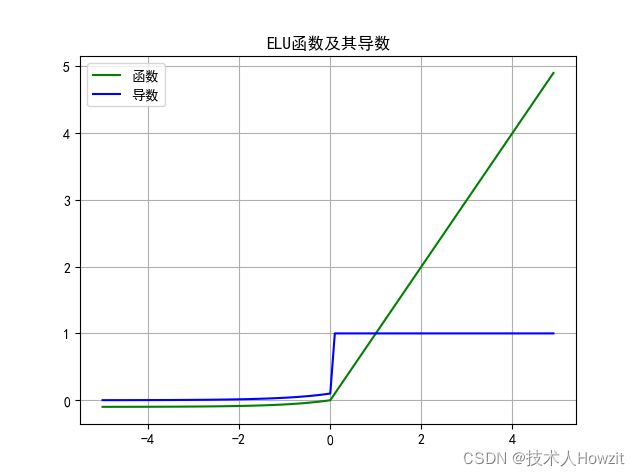
2.5 ELU
- 公式: f ( x ) = { x i f x > 0 ; α ( e x − 1 ) i f x ≤ 0 f(x)=\begin{cases}x\quad if \quad x>0;\\\alpha(e^x-1) \quad if\quad x\leq0\end{cases} f(x)={xifx>0;α(ex−1)ifx≤0
- 导数: f ( x ) ′ = { 1 i f x > 0 ; f ( x ) + α i f x ≤ 0 f(x)'=\begin{cases}1\quad if \quad x>0;\\f(x)+\alpha \quad if\quad x\leq0\end{cases} f(x)′={1ifx>0;f(x)+αifx≤0
- 代码实现:
class Elu:
def __init__(self, alpha=0.1):
self.alpha = alpha
def __call__(self, x):
return np.where(x > 0, x, self.alpha * (np.exp(x) - 1))
def gradient(self, x):
return np.where(x > 0, 1, self.__call__(x) + self.alpha)
3 激活函数最新进展
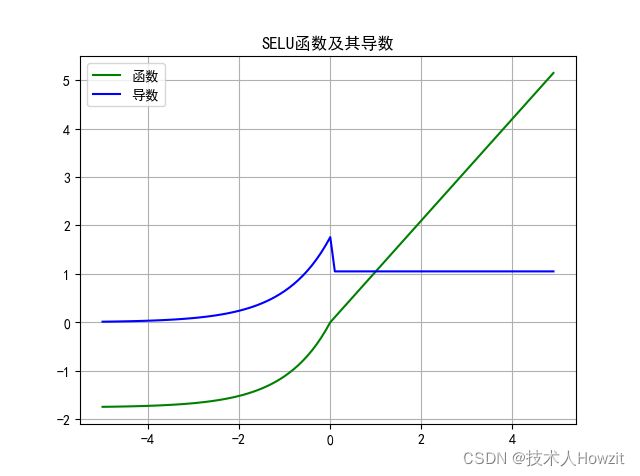
3.1 SELU(scaled ELU)
Klambauer 等人在 2017 年的一篇论文中介绍了 Scaled ELU 或 SELU 激活。它是ELU的缩放版,其公式如下:
- 公式: s e l u ( x ) = λ { x i f x > 0 α e x − α i f x ≤ 0 selu(x)=\lambda\begin{cases}x\quad if \quad x>0\\{\alpha e^x-\alpha\quad if\quad x\leq0}\end{cases} selu(x)=λ{xifx>0αex−αifx≤0
其中 α \alpha α默认为1.6732, λ \lambda λ为1.0507。
- 导数: s e l u ( x ) = λ { 1 i f x > 0 α e x i f x ≤ 0 selu(x)=\lambda\begin{cases}1\quad if \quad x>0\\{\alpha e^x\quad if\quad x\leq0}\end{cases} selu(x)=λ{1ifx>0αexifx≤0
- 实现:
class SELU:
# Reference : https://arxiv.org/abs/1706.02515,
# https://github.com/bioinf-jku/SNNs/blob/master/SelfNormalizingNetworks_MLP_MNIST.ipynb def __init__(self):
self.alpha = 1.6732632423543772848170429916717
self.scale = 1.0507009873554804934193349852946
def __call__(self, x):
return self.scale * np.where(x > 0, x, self.alpha * (np.exp(x) - 1))
def gradient(self, x):
return self.scale * np.where(x >= 0.0, 1, self.alpha * np.exp(x))
def __str__(self):
return "SELU"
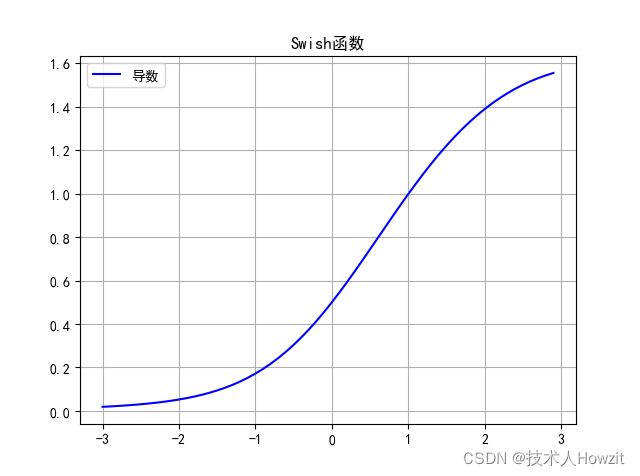
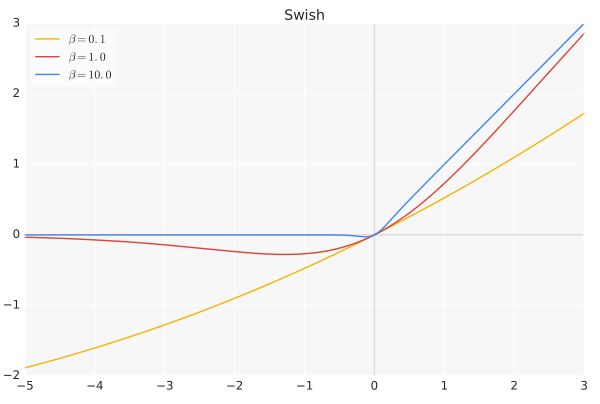
3.2 Swish函数
由 Ramachandran 等人于 2017 年 Google Brain 上的发现。 非常简单:它只是将输入乘以自己的 sigmoid。
- 公式: s w i s h ( x ) = x ∗ s i g m o i d ( β x ) swish(x)=x*sigmoid(\beta x) swish(x)=x∗sigmoid(βx)
其中, β \beta β可常数,可训练,它也影响着模型的准确率,Swish具备无上界有下界、平滑、非单调的特性。 - 导数: s w i s h ( x ) ′ = s i g m o i d ( β ∗ x ) + β ∗ x s i g m o i d ( x ) ′ swish(x)'=sigmoid(\beta*x)+\beta*xsigmoid(x)' swish(x)′=sigmoid(β∗x)+β∗xsigmoid(x)′
- 实现:
class Swish:
def __init__(self, beta):
self.beta = beta
def __call__(self, x):
return x * self.sigmoid(self.beta * x)
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def gradient(self, x):
return (1 + np.exp(-self.beta * x) - self.beta * x * np.exp(-x)) / np.square(1 + np.exp(-x))
def __str__(self):
return 'Swish'
-
特性:
- Swish 具有一定ReLU函数的优点;
- Swish 具有一定Sigmoid函数的优点;
- Swish 函数可以看做是介于线性函数与ReLU函数之间的平滑函数。
3.3 Mish函数
- 公式: f ( x ) = x ∗ t a n h ( l n ( 1 + e x ) ) f(x)=x*tanh(ln(1+e^x)) f(x)=x∗tanh(ln(1+ex))
- 导数: f ( x ) ′ = s e c h ( s o f t _ p l u s ( x ) ∗ s e c h ( s o f t _ p l u s ( x ) ∗ x ∗ s i g m o i d ( x ) + t a n h ( s o f t _ p l u s ( x ) ) f(x)'=sech(soft\_plus(x)*sech(soft\_plus(x)*x*sigmoid(x)+tanh(soft\_plus(x)) f(x)′=sech(soft_plus(x)∗sech(soft_plus(x)∗x∗sigmoid(x)+tanh(soft_plus(x)),where s o f t P l u s = l n ( 1 + e x ) , s i g m o i d ( x ) = 1 / ( 1 + e x ) softPlus = ln(1+e^x),sigmoid(x)=1/(1+e^x) softPlus=ln(1+ex),sigmoid(x)=1/(1+ex)
- 实现:
def sech(x):
"""sech函数"""
return 2 / (np.exp(x) + np.exp(-x))
def sigmoid(x):
"""sigmoid函数"""
return 1 / (1 + np.exp(-x))
def soft_plus(x):
"""softplus函数"""
return np.log(1 + np.exp(x))
def tan_h(x):
"""tanh函数"""
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
class Mish:
def __call__(self, x):
return x * tan_h(soft_plus(x))
def gradient(self, x):
return sech(soft_plus(x)) * sech(soft_plus(x)) * x * sigmoid(x) + tan_h(soft_plus(x))
def __str__(self):
return 'Mish'
下面把完整的代码贴出来,供大家去参考:
import matplotlib.pyplot as plt
import numpy as np
"""https://blog.csdn.net/hhhhhhhhhhwwwwwwwwww/article/details/120301830"""
# 显示中文
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
def sech(x):
"""sech函数"""
return 2 / (np.exp(x) + np.exp(-x))
def sigmoid(x):
"""sigmoid函数"""
return 1 / (1 + np.exp(-x))
def soft_plus(x):
"""softplus函数"""
return np.log(1 + np.exp(x))
def tan_h(x):
"""tanh函数"""
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
class Sigmoid:
def __call__(self, x):
return 1 / (1 + np.exp(-x))
def gradient(self, x):
return self.__call__(x) * (1 - self.__call__(x))
def __str__(self):
return "Sigmoid"
class Tanh:
def __call__(self, x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def gradient(self, x):
return 1 - np.square(self.__call__(x))
def __str__(self):
return "tanh"
class ReLu:
def __call__(self, x):
return np.where(x > 0, x, 0)
def gradient(self, x):
return np.where(x > 0, 1, 0)
def __str__(self):
return "ReLu"
class LeakReLu:
def __init__(self, alpha=0.03):
self.alpha = alpha
def __call__(self, x):
return np.where(x > 0, x, self.alpha * x)
def gradient(self, x):
return np.where(x > 0, 1, self.alpha)
def __str__(self):
return "ReLu"
class Elu:
def __init__(self, alpha=0.1):
self.alpha = alpha
def __call__(self, x):
return np.where(x > 0, x, self.alpha * (np.exp(x) - 1))
def gradient(self, x):
return np.where(x > 0, 1, self.__call__(x) + self.alpha)
def __str__(self):
return "ELU"
class SELU:
# Reference : https://arxiv.org/abs/1706.02515,
# https://github.com/bioinf-jku/SNNs/blob/master/SelfNormalizingNetworks_MLP_MNIST.ipynb def __init__(self):
self.alpha = 1.6732632423543772848170429916717
self.scale = 1.0507009873554804934193349852946
def __call__(self, x):
return self.scale * np.where(x > 0, x, self.alpha * (np.exp(x) - 1))
def gradient(self, x):
return self.scale * np.where(x >= 0.0, 1, self.alpha * np.exp(x))
def __str__(self):
return "SELU"
class Swish:
def __init__(self, beta):
self.beta = beta
def __call__(self, x):
return x * sigmoid(self.beta * x)
def gradient(self, x):
return (1 + np.exp(-self.beta * x) - self.beta * x * np.exp(-x)) / np.square(1 + np.exp(-x))
def __str__(self):
return 'Swish'
class Mish:
def __call__(self, x):
return x * tan_h(soft_plus(x))
def gradient(self, x):
return sech(soft_plus(x)) * sech(soft_plus(x)) * x * sigmoid(x) + tan_h(soft_plus(x))
def __str__(self):
return 'Mish'
if __name__ == "__main__":
function = Mish()
l = np.arange(-3, 3, step=0.1)
plt.grid()
plt.plot(l, function(x=l), label="函数", color="g")
plt.plot(l, function.gradient(l), label="导数", color="b")
plt.legend()
plt.title(function.__str__() + "函数及导数")
plt.show()
4 总结
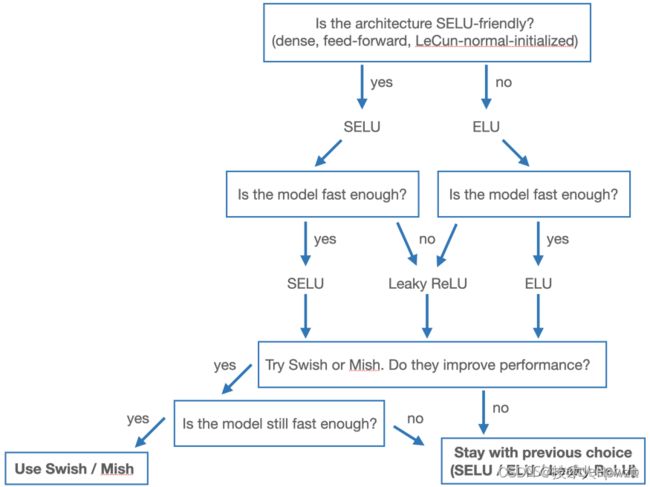
面对这么的激活函数,我们该如何选择呢?Geron 在他的精彩著作《使用 Scikit-Learn 和 TensorFlow 进行机器学习实践》中陈述了以下一般规则:
SELU > ELU > Leaky ReLU > ReLU
使用总结:
-
sigmoid 激活函数计算量大(在正向传播和反向传播中都包含幂运算和除法);
-
Sigmoid 导数取值范围是[0, 0.25],由于神经网络反向传播时的“链式反应”,很容易就会出现梯度消失的情况。例如对于一个10层的网络, 根据 0.2 5 10 = 0.000000954 0.25^{10}=0.000000954 0.2510=0.000000954,第10层的误差相对第一层卷积的参数 W 1 W_1 W1的梯度将是一个非常小的值,这就是所谓的“梯度消失”。
-
Sigmoid 的输出不是0均值(即zero-centered);这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入,随着网络的加深,会改变数据的原始分布。
-
如果输出是 0、1 值(二分类问题),则输出层选择 sigmoid 函数,然后其它的所有单元都选择 Relu 函数。
-
如果在隐藏层上不确定使用哪个激活函数,那么通常会使用 Relu 激活函数。有时,也会使用 tanh 激活函数,但 Relu 的一个优点是:当是负值的时候,导数等于 0。
-
sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
-
tanh 激活函数:tanh 是非常优秀的,几乎适合所有场合。
-
ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者 Leaky ReLu,再去尝试其他的激活函数。
1) 解决了gradient vanishing问题 (在正区间)
2)计算速度非常快,只需要判断输入是否大于0
3)收敛速度远快于 sigmoid 和tanh -
如果遇到了一些死的神经元,我们可以使用 Leaky ReLU 函数。
为了更加清晰,我把列举一些激活函数:
| 激活函数 | 公式 | 参数说明 |
|---|---|---|
| linear | f ( x ) = x f(x)=x f(x)=x | |
| sigmoid | f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1 | |
| tanh | f ( x ) = e x − e − x e x + e − x = s i n h ( x ) c o s h ( x ) f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{sinh(x)}{cosh(x)} f(x)=ex+e−xex−e−x=cosh(x)sinh(x) | |
| relu | r e l u ( x ) = { x i f x > 0 0 i f x ≤ 0 relu(x)=\begin{cases}x\quad if \quad x>0\\{0\quad if\quad x\leq0}\end{cases} relu(x)={xifx>00ifx≤0 | |
| leaky_relu | f ( x ) = { x i f x > = 0 x ∗ α i f x < = 0 f(x)=\begin{cases}{x \quad if \quad x>=0}\\{x*\alpha \quad if \quad x<=0}\end{cases} f(x)={xifx>=0x∗αifx<=0 | 默 认 α 默认\alpha 默认α 为0.03 |
| elu | e l u ( x ) = { x i f x > 0 ; a ( e x − 1 ) i f x ≤ 0 elu(x)=\begin{cases}x\quad if \quad x>0;\\a(e^x-1) \quad if\quad x\leq0\end{cases} elu(x)={xifx>0;a(ex−1)ifx≤0 | a为1 |
| selu | s e l u ( x ) = λ { x i f x > 0 α e x − α i f x ≤ 0 selu(x)=\lambda\begin{cases}x\quad if \quad x>0\\{\alpha e^x-\alpha\quad if\quad x\leq0}\end{cases} selu(x)=λ{xifx>0αex−αifx≤0 | α \alpha α默认为1.6732, λ \lambda λ为1.0507 |
| softplus | f ( x ) = l o g ( e x + 1 ) f(x)=log(e^x+1) f(x)=log(ex+1) | |
| swish | f ( x ) = x ⋅ s i g m o i d ( β x ) f(x)=x⋅sigmoid(βx) f(x)=x⋅sigmoid(βx) | |
| Mish | f ( x ) = x ∗ t a n h ( l n ( 1 + e x ) ) f(x)=x∗tanh(ln(1+e^x)) f(x)=x∗tanh(ln(1+ex)) | |
| softsign | f ( x ) = x ∥ x ∥ + 1 f(x)=\frac{x}{\|x\|+1} f(x)=∥x∥+1x | |
| exponential | f ( x ) = e x f(x)=e^x f(x)=ex | |
| hard_sigoid | f ( x ) = { 0 i f x < − 2.5 1 i f x > 2.5 0.2 ∗ x + 0.5 i f − 2.5 < = x < = 2.5 f(x)=\begin{cases}0 \quad if \quad x<-2.5\\1 \quad if \quad x>2.5\\0.2*x+0.5 \quad if \quad -2.5<=x<=2.5\end{cases} f(x)=⎩⎪⎨⎪⎧0ifx<−2.51ifx>2.50.2∗x+0.5if−2.5<=x<=2.5 |
参考:
- 激活函数总结
- 常用激活函数(激励函数)理解与总结
- 激活函数其实并不简单:最新的激活函数如何选择?
- 神经网络学习小记录57——各类激活函数Activation Functions介绍与优缺点分析