【深度学习笔记—1】:激活函数
✨博客主页:米开朗琪罗~
✨博主爱好:羽毛球
✨年轻人要:Living for the moment(活在当下)!
推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】
目录
- 一、激活函数
-
- 1.1 激活函数的位置
- 1.2 激活函数的作用
- 1.3 激活函数的性质
- 二、激活函数种类
-
- 2.1 线性(Linear)函数
- 2.2 Sigmoid函数
- 2.3 双曲正切函数(tanh)
- 2.4 ReLU函数
- 2.5 Leak ReLU函数
- 2.6 ELU激活函数
- 2.7 PReLU函数
- 2.8 Softmax函数
- 三、如何选择正确的激活函数
想必对于深度学习或多或少学过的童鞋们一定知道激活函数,本文就详细介绍激活函数的种类都有哪些,我们又该如何正确选择激活函数。
一、激活函数
1.1 激活函数的位置
下图给出了一个神经元模型,可以看到输入信号经过加权与求和后,又通过了φ函数,这个φ函数就是激活函数。
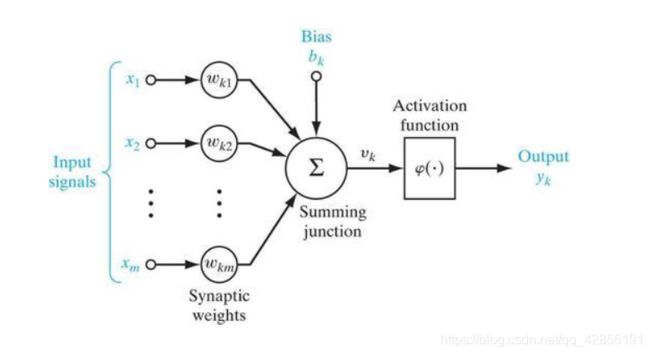
1.2 激活函数的作用
如果神经网络没有激活函数,那么它只能表示为线性模型,表达能力有限。
加入了激活函数之后,便引入了非线性因素,可以表达许多复杂的数据分布。
1.3 激活函数的性质
● 单调性:为了保证单层模型具有凸函数性能,而凸函数容易优化,不存在鞍点或者局部最优解这种问题,因此我们要求激活函数要具有单调性。
● 可微性:深度学习的优化算法基本采用的都是梯度下降算法,因此激活函数必须可微。
● 输出值范围:由神经元的模型我们可以知道,输出值的大小最后由激活函数决定,那么我们可以这么理解,激活函数决定该神经元能否被输出。
二、激活函数种类
2.1 线性(Linear)函数
函数公式:
f ( x ) = a x + b f(x)=ax+b f(x)=ax+b
函数图:
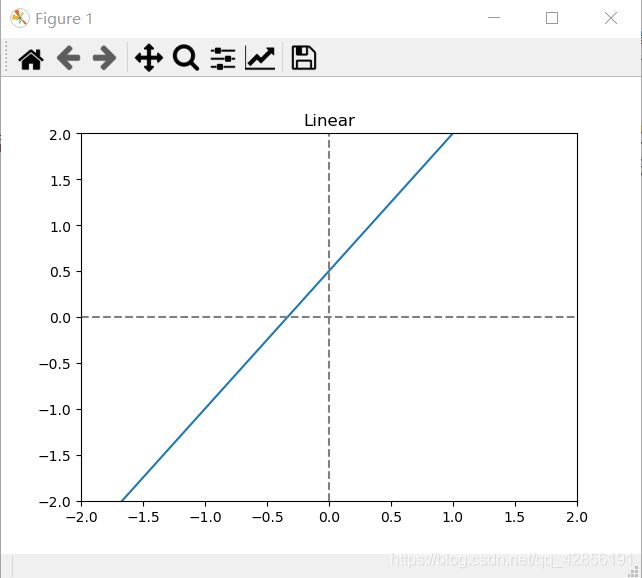
函数介绍:
由函数图和函数公式可知,线性函数的输入与输出成比例,因此,线性变换与线性回归类似。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def Linear(x, a=1.5, b=0.5):
return a * x + b
x = np.arange(-2, 2, 0.1)
y = Linear(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-2, 2])
ax.set_ylim([-2, 2])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("Linear")
plt.show()
2.2 Sigmoid函数
函数公式:
s ( x ) = 1 1 + e − a x s(x)=\frac{1}{1+e^{-ax}} s(x)=1+e−ax1
函数图:

函数介绍:
由数学关系式可知,Sigmoid函数的输出范围为(0,1),因此,它可以类比为概率,表示神经元是否被激活。
优点:
● 输出范围(0,1),函数连续且单调递增,优化稳定;
● 求导方便;
● 可类比为概率,用于输出层神经元激活与否的判定。
缺点:
● Sigmoid函数易饱和,容易出现梯度消失;
● 幂运算,计算量大。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def Sigmoid(x):
return 1 / (1 + np.exp(-1 * x))
x = np.arange(-3, 3, 0.1)
y = Sigmoid(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 3])
ax.set_ylim([-0.5, 2])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("Sigmoid")
plt.show()
2.3 双曲正切函数(tanh)
函数公式:
t a n h ( x ) = s i n h ( x ) c o s h ( x ) = e x − e − x e x + e − x tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} tanh(x)=cosh(x)sinh(x)=ex+e−xex−e−x
函数图:
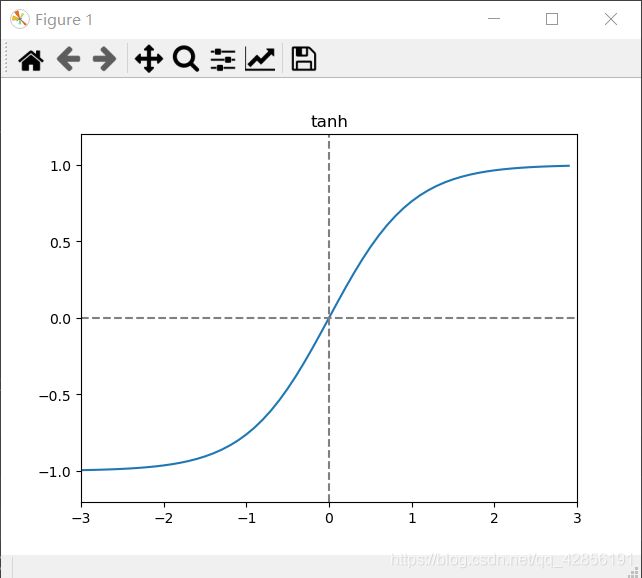
函数介绍:
tanh函数与Sigmoid函数类似,但tanh函数存在负数区域,也就比Sigmoid函数能处理更多的负数部分数据。
优点:
● 函数均值为0,比Sigmoid函数有更大优势;
● 函数比Sigmoid函数收敛速度更快。
缺点:
● 仍然易饱和,存在梯度消失的问题。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def tanh(x):
return np.tanh(x)
x = np.arange(-3, 3, 0.1)
y = tanh(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 3])
ax.set_ylim([-1.2, 1.2])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("tanh")
plt.show()
2.4 ReLU函数
函数公式:
r e l u ( x ) = m a x ( 0 , x ) relu(x)=max(0,x) relu(x)=max(0,x)
函数图:
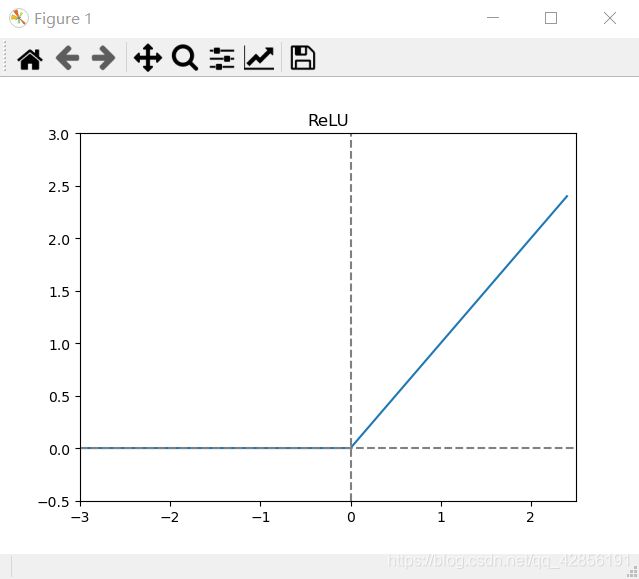
函数介绍:
ReLU函数目前使用是较多的,该函数与Sigmoid函数的类比概率性质相似,只不过ReLU函数是带阈值的概率类比。
优点:
● ReLU函数收敛速度更快;
● 梯度不会饱和,也就缓解了梯度消失问题;
● 计算速度更快。
缺点:
● 神经元有死亡的可能性,因为函数在x<0的时候梯度为0,该神经元可能不会被激活,会出现权重无法更新的现象。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def ReLU(x):
return np.maximum(0, x)
x = np.arange(-3, 2.5, 0.1)
y = ReLU(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 2.5])
ax.set_ylim([-0.5, 3])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("ReLU")
plt.show()
2.5 Leak ReLU函数
函数公式:
f ( x ) = { x x ⩾ 0 a x x < 0 f(x)=\left\{ \begin{array}{rcl} x & & {x\geqslant 0}\\ ax & & {x<0} \end{array} \right. f(x)={xaxx⩾0x<0
函数图:
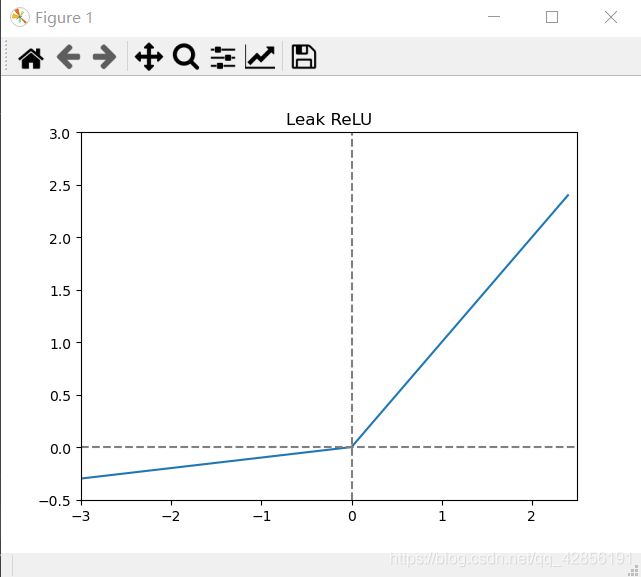
函数介绍:
与Relu的不同之处在于负轴保留了非常小的常数斜率,使得输入信息小于0时,信息没有完全丢掉,进行了相应的保留。
优点:
● 避免了ReLU函数出现的神经元死亡的问题;
● 收敛速度较快。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def Leak_ReLU(x, a=0.1):
return np.maximum(a * x, x)
x = np.arange(-3, 2.5, 0.1)
y = Leak_ReLU(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 2.5])
ax.set_ylim([-0.5, 3])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("Leak ReLU")
plt.show()
2.6 ELU激活函数
函数公式:
f ( x ) = { x x > 0 α ( e x − 1 ) x ⩽ 0 f(x)=\left\{ \begin{array}{rcl} x & & {x>0}\\ \alpha( e^{x}-1) & & {x\leqslant 0} \end{array} \right. f(x)={xα(ex−1)x>0x⩽0
函数图:

函数介绍:
ELU函数在输入数据为负数的情况下,也是会有输出的,不会像ReLU函数一样,造成神经元的死亡。
优点:
● 不会出现神经元的死亡现象;
● ELU函数可以加速训练并且可以提高分类的准确率;
● 收敛速度较快。
缺点:
● 计算量变大。
函数代码:
import math
import matplotlib.pyplot as plt
import numpy as np
def ELU(x, alpha=1):
a = x[x > 0]
b = alpha * (math.e ** (x[x < 0]) - 1)
result = np.concatenate((b, a), axis=0)
return result
x = np.arange(-3, 2.5, 0.1)
y = ELU(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 2.5])
ax.set_ylim([-1.5, 3])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title(ELU)
plt.show()
2.7 PReLU函数
函数公式:
f ( x ) = m a x ( a x , x ) f(x)=max(ax,x) f(x)=max(ax,x)
函数图:
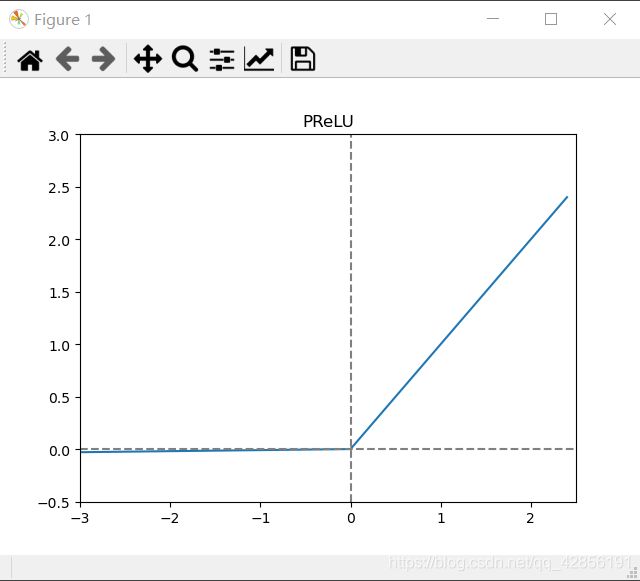
函数介绍:
和ELU类似,在负数区域函数存在一定的斜率,且负数区域的函数是线性的,不会造成神经元的死亡。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def PReLU(x, a=0.01):
return np.maximum(a * x, x)
x = np.arange(-3, 2.5, 0.1)
y = PReLU(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-3, 2.5])
ax.set_ylim([-0.5, 3])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("PReLU")
plt.show()
2.8 Softmax函数
函数公式:
s o f t m a x ( x j ) = e x j ∑ k = 1 K e x k softmax(x_{j})=\frac{e^{x_{j}}}{\sum_{k=1}^{K}e^{x_{k}}} softmax(xj)=∑k=1Kexkexj
函数图:
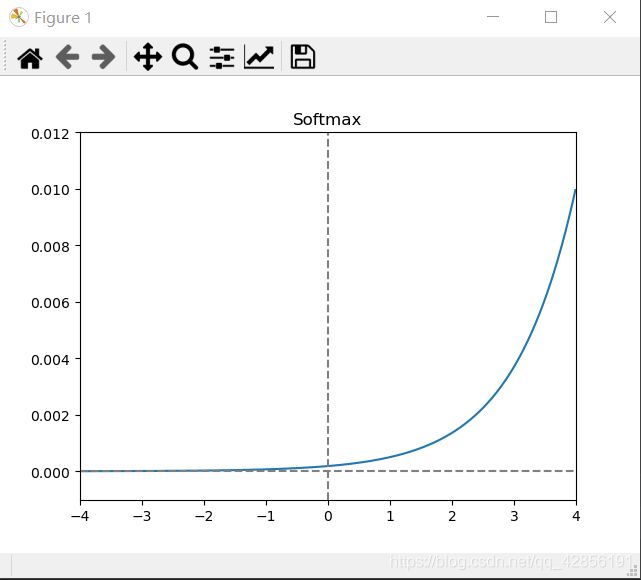
函数介绍:
在数学,尤其是概率论和相关领域中,归一化指数函数,或称Softmax函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。该函数多于多分类问题中。
参考:百度百科
优点:
● 可用作多分类问题,且计算量小。
函数代码:
import numpy as np
import matplotlib.pyplot as plt
def Softmax(x):
return np.exp(x) / np.sum(np.exp(x))
x = np.arange(-4, 4, 0.01)
y = Softmax(x)
plt.plot(x, y)
ax = plt.gca()
ax.set_xlim([-4, 4])
ax.set_ylim([-0.001, 0.012])
ax.axhline(0, linestyle='--', color='gray')
ax.axvline(0, linestyle='--', color='gray')
plt.title("Softmax")
plt.show()
三、如何选择正确的激活函数
● 深度学习往往需要大量时间来处理大量数据,模型的收敛速度是尤为重要的。所以,总体上来讲,训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度;
● 如果使用 ReLU,那么一定要小心设置 learning rate,而且要注意不要让网络出现很多 “dead” 神经元,如果这个问题不好解决,那么可以试试 Leaky ReLU、PReLU 或者 Maxout;
● 最好不要用 sigmoid,你可以试试 tanh,不过可以预期它的效果会比不上 ReLU 和 Maxout。
● 如果遇到神经网络训练时收敛速度较慢,或者梯度爆炸、消失等问题,都可以选择加入BN层。
参考:https://blog.csdn.net/tyhj_sf/article/details/79932893
希望本文对大家关于激活函数的理解有所帮助!