C语言百日刷题第六天
C语言百日刷题第六天
-
-
- 51.鸡兔同笼问题
- 52.输出所有形如aabb的完全平方数
- 53.3n+1问题
- 54.输出100~999的所有水仙花数
- 55.韩信点兵
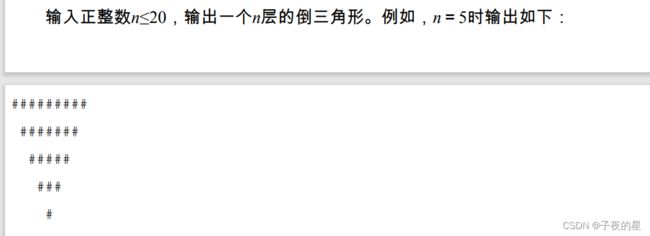
- 56.倒三角形
- 57.求子序列的和
- 58.分数化小数
- 59.开灯问题
- 60.蛇形填数
-
51.鸡兔同笼问题

分析:小学生数学问题。设鸡为a个,兔为b个,建立二元一次方程组:
可以解的: a=(4n-m)/2, b=n-a。
但是要考虑无解的情况。当解出的a,b是小于0或者腿数位奇数的时候是不符合实际情况的。
#include52.输出所有形如aabb的完全平方数
int m = floor(sqort(n)+0.5);//n是需要判断的数
if(m*m==n)
printf("是完全平方数");
以为在大量计算的时候,可能会发生误差,由于误差可能会使1变为0.99999999999999999,但是floor会使0.9999999999的结果为0。为了不让这种情况发生,我们加上0.5,改为四舍五入。这样就可以避免以上的情况发生。
根据方法一写出的代码:
#include方法二:
int a = n/100;//n是需要判断的数,n/100就是前两位的数字
int b = n%100;//n%100就是后两位数字
if(a/10==a%10&&b/10==b%10)
printf("是完全平方数");
根据方法二写出的代码:
#include53.3n+1问题
#include54.输出100~999的所有水仙花数
#include55.韩信点兵
#include56.倒三角形
#include 57.求子序列的和
#include58.分数化小数
#includeprintf(“% * . * lf\n”, a, b, c); 会输出a个字宽保留b位小数的浮点数运算结果c。
该解法会出现精度问题,所有使用下面的数学解法。
#include 59.开灯问题
#include“memset(a,0,sizeof(a))”的作用是把数组a清零,它也在string.h中定义。虽然也能
用for循环完成相同的任务,但是用memset又方便又快捷。另一个技巧在输出:为了避免输出
多余空格,设置了一个标志变量first,可以表示当前要输出的变量是否为第一个。第一个变 量前不应有空格,但其他变量都有。
60.蛇形填数
#include解法二:
#include