MATLAB三维曲线与曲面绘图

三维曲线

plot3函数

plot3(x, y, z) 其中，参数x、y、z组成一组曲线的坐标。
若 x , y, z 是等长行向量，则根据向量的位置确定坐标， 如 (x1, y1, z1)

x=[0.2, 1.8, 2.5]; 
y=[1.3, 2.8, 1.1]; 
z=[0.4, 1.2, 1.6]; 
plot3(x, y, z) 
grid on 
axis([0, 3, 1, 3, 0, 2])

plot3(x,y,z)函数参数的变化形式

（1）参数 X、Y、Z是同型矩阵时，以 X、Y、Z对应列元素绘制曲线， 曲线条数等于矩阵列数。
(2) 参数 X、Y、Z中有向量，也有矩阵时，向量的长度应与矩阵相符。

t=0:0.01:2*pi;
t=t';
x=[t, t, t, t, t];
y=[sin(t), sin(t)+1, sin(t)+2, sin(t)+3, sin(t)+4];
z=x;
plot3(x,y,z)
% 这个例子也可以采用以下代码实现。
t=0:0.01:2*pi;
x=t;
y=[sin(t); sin(t)+1; sin(t)+2; sin(t)+3; sin(t)+4];
z=x;
plot3(x,y,z)

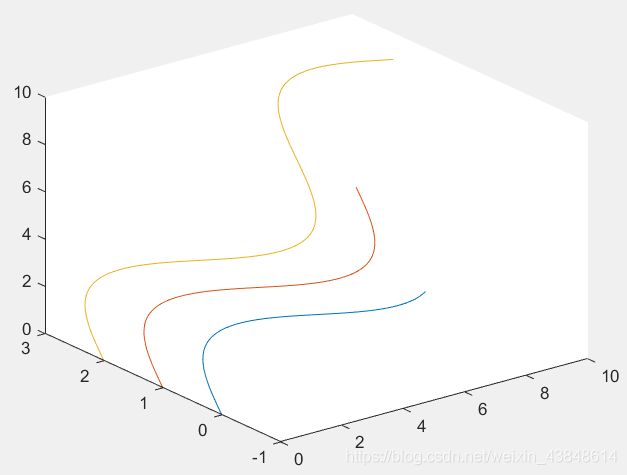
（3）含多组输入参数的plot3函数

plot3(x1, y1, z1, x2, y2, z2, …, xn, yn, zn)

每一组x、y、z向量构成一组数据点的坐标，绘制一条曲线。

t1=0:0.01:1.5*pi; 
t2=0:0.01:2*pi; 
t3=0:0.01:3*pi; 
plot3(t1,sin(t1),t1, t2,sin(t2)+1,t2, t3,sin(t3)+2,t3)

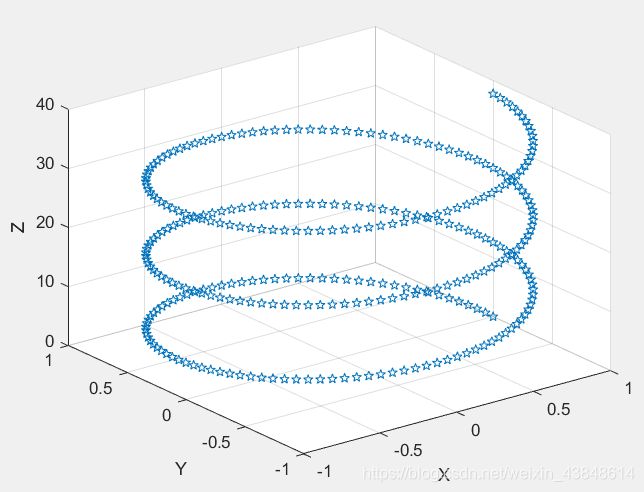
含选项的plot3函数

plot3(x, y, z, 选项) 

选项用于指定曲线的线型、颜色和数据点标记。

t=0:pi/50:6*pi;
x=cos(t);
y=sin(t);
z=2*t;
plot3(x,y,z,'p')
xlabel('X'),ylabel('Y'),zlabel('Z');
grid on

fplot3函数

fplot3(funx, funy, funz, tlims)

其中，funx、funy、funz代表定义曲线x、y、z坐标的函数，通 常采用函数句柄的形式。tlims为参数函数自变量的取值范围，用二元向量[tmin, tmax]描述，默认为[-5, 5]。

xt = @(t) exp(-t/10).*sin(5*t);
yt = @(t) exp(-t/10).*cos(5*t);
zt = @(t) t;
fplot3(xt, yt, zt, [-12, 12])

三维曲面

(一)、平面网格数据的生成

(1) 利用矩阵运算生成。

x = 2:6; 
y = (3:8)'; 
X = ones(size(y))*x;% 列向量在前，行向量在后生成矩阵
Y = y*ones(size(x));

(2) 利用meshgrid函数生成。

[X,Y]=meshgrid(x,y);

其中，参数x、y为向量，存储网格点坐标的X、Y为矩阵。

x = 2:1:6; 
y = (3:1:8)';
[X, Y] = meshgrid(x, y);

第3行命令生成的网格坐标矩阵X、Y与方法(1)得到的相同。

% 绘制空间曲线.

x = 2:6; 
y = (3:8)';
[X, Y] = meshgrid(x, y);
Z = randn(size(X));
plot3(X,Y,Z)
grid on;

注： 上述 X， Y， Z， 为同型矩阵，按列画曲线， 曲线条数等于列数

(二)、绘制三维曲面的函数

(1) mesh函数和surf函数

mesh(x, y, z, c) 三维网格图			
surf(x, y, z, c) 三维曲面图

  一般 x，y， z 一般为同型矩阵，其中，x、y是网格坐标矩阵，z是网格点上的高度矩阵，c 用于指定在不同高度下的曲面颜色。c 省略时，颜色的设定正比于图形的高度。

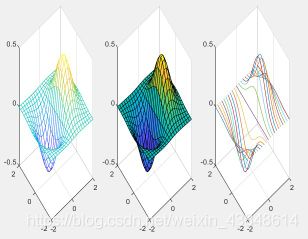
% 绘制三维曲面图。  
t = -2:0.2:2; 
[X, Y] = meshgrid(t);
Z = X .* exp(-X.^2 - Y.^2);
subplot(1,3,1)
mesh(X,Y,Z); 
subplot(1,3,2)
surf(X,Y,Z); 
subplot(1,3,3)
plot3(X,Y,Z); 
grid on

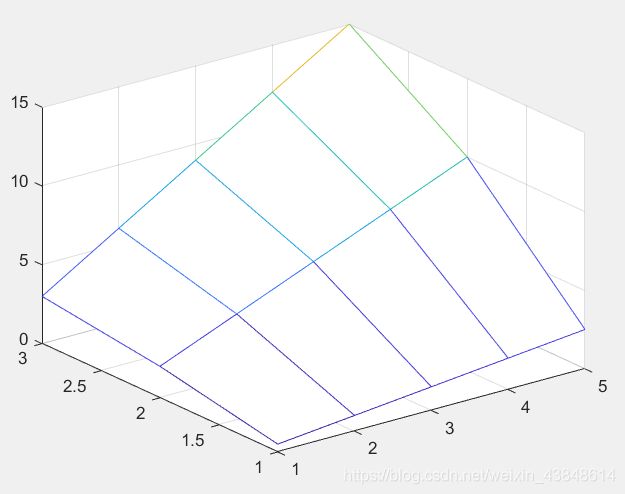
mesh函数和surf函数的其他调用格式：

mesh(z, c)
surf(z, c)
当x、y省略时，z矩阵的第2维下标当作x轴坐标，z矩阵的第1维下标当作y轴坐标。

t = 1:5; 
z= [0.5*t; 2*t; 3*t];
mesh(z);

(2) meshc, meshz, surfc, surfl

带等高线的三维网格曲面函数meshc
带底座的三维网格曲面函数meshz
具有等高线的曲面函数surfc
具有光照效果的曲面函数surfl

例、 用4种方式绘制函数=(−1)²⁺⁽⁻²⁾2−1的曲面图。其中，x∈[0,2]，y∈[1,3].

[x,y]=meshgrid(0:0.1:2,1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
meshc(x,y,z);title('meshc(x,y,z)')
subplot(2,2,2);
meshz(x,y,z);title('meshz(x,y,z)')
subplot(2,2,3);
surfc(x,y,z);title('surfc(x,y,z)')
subplot(2,2,4);
surfl(x,y,z); title('surfl(x,y,z)')

例： X^2+ Y^2 + Z^2

clc,clear;
x = linspace(-2, 2, 40);    %等间隔分割点
y = x;
z = x;
[X, Y, Z] = meshgrid(x, y, z);  % 网格点化
w = X.^2 + Y.^2 + Z.^2;         % 函数
slice(X, Y, Z, w, [-1, 0, 1], [-1, 0, 1], [-1, 0, 1])   %切片画图
colorbar                        % 颜色条

标准三维曲面

sphere函数, cylinder函数

（1）sphere函数 [x,y,z]=sphere(n)
产生3个(n+1)阶的方阵，采用这3个矩阵可以绘制出圆心位于原点、半径为1的单位球体。
（2）cylinder函数 [x,y,z]=cylinder(R, n)
其中，参数R是一个向量，存放柱面各个等间隔高度上的半径， n表示在圆柱圆周上有n个间隔点，默认有20个间隔点。

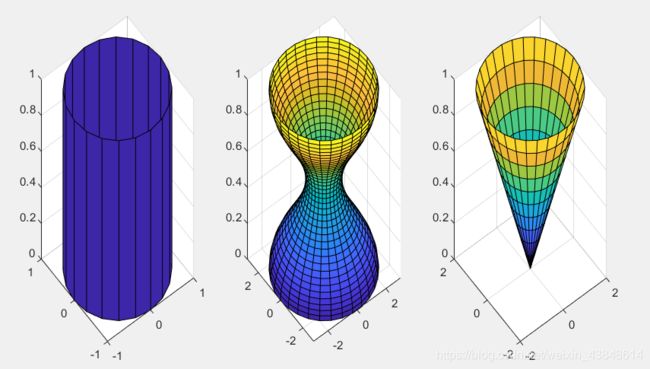
用cylinder函数分别绘制柱面、花瓶和圆锥面。

subplot(1,3,1);
[x,y,z]=cylinder;
surf(x,y,z);
subplot(1,3,2);
t=linspace(0,2*pi,40);
[x,y,z]= cylinder(2+cos(t),30);
surf(x,y,z);
subplot(1,3,3);
[x,y,z]= cylinder(0:0.2:2,30);
surf(x,y,z);

例 用cylinder函数绘制两个相互垂直且直径相等的圆柱面的相交图形。

[x,y,z]= cylinder(1,60);
z=[-1*z(2,:);z(2,:)];
surf(x,y,z)
hold on
surf(y,z,x)
axis equal

peaks函数

peaks(n)
peaks(V)
peaks(x,y)
peaks

p1=peaks(10); 
p2=peaks; 
p3=peaks(-3:0.2:3); 
[x,y]=meshgrid(-2:0.1:2, 0:0.1:5); 
p4=peaks(x,y);

peaks 函数的返回值，可以作为 mesh 等三维函数的参数
p1=peaks(10); x和y方向将区间 [-3, 3] 等分为9份，生成10阶方阵
p2=peaks; 生成一个一个49阶的方阵
p3=peaks(-3:0.2:3); 一个与31个元素的行向量，生成一个31阶方阵
p4=peaks(x,y); 两个同型矩阵，将生成一个与 x y 同型的矩阵

参数方程的绘制

fmesh函数和fsurf函数

由三个参数方程，参数方程有两个自变量

用于绘制参数方程定义的曲面
fsurf(funx, funy, funz, uvlims)
fmesh(funx, funy, funz, uvlims)
其中，funx、funy、funz代表定义曲面x、y、z坐标的函数，通常采用函数句柄的形式。uvlims为funx、funy和funz的自变量的取值范围，用4元向量[umin, umax, vmin, vmax]描述 ，默认为[-5, 5, -5, 5]。

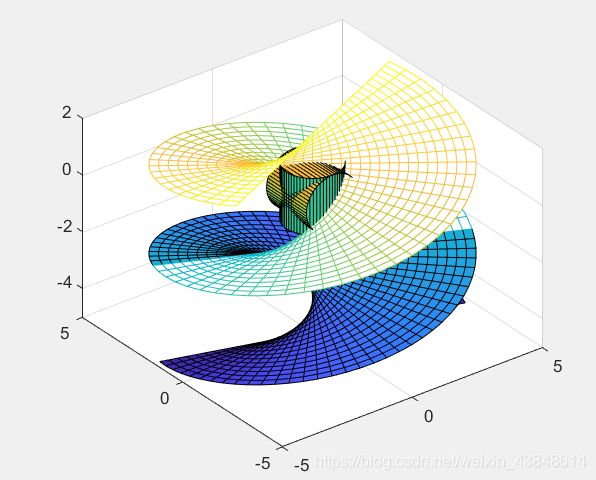
%例6 绘制螺旋曲面。

funx = @(u,v) u.*sin(v);
funy = @(u,v) -u.*cos(v);
funz = @(u,v) v;
fsurf(funx,funy,funz,[-5 5 -5 -2])
hold on
fmesh(funx,funy,funz,[-5 5 -2 2])
hold off

例、绘制三维曲面图z=sin(x+sin y)-x/10。

x = linspace(-3,3);
y = linspace(-4,4);
[X,Y] = meshgrid(x,y);
z = sin(x+sin(y))-x./10;
disp(z);
disp(size(x));
disp(size(y));
disp(size(X));
disp(size(z));
Z = ones(100, 100).*z;
disp(size(Z))
surf(X,Y,Z)

图形修饰处理

视点处理  色彩处理  图形的裁剪处理

view命令用来控制三维图形的观察点和视角，它的使用格式如下：

调用格式 说明

view(az,el) 给三维空间图形设置观察点的方位角az与仰角el

view([az,el]) 同上

view([x,y,z]) 将点(x,y,z)设置为视点

view(2) 设置默认的二维形式视点，其中az = 0,el = 90,即从z轴上方观看

view(3) 设置默认的三维形式视点，其中az = -37.5, ell = 30

view(T) 根据转换矩阵T设置视点，其中T为4*4阶的矩阵，如同用命令viewmtx生成的透视转换矩阵一样（注意：在2014版本中，这条命令好像没了）

[az,el]=view 返回当前的方位角az与仰角el

T = view 返回当前的4*4阶的转换矩阵T

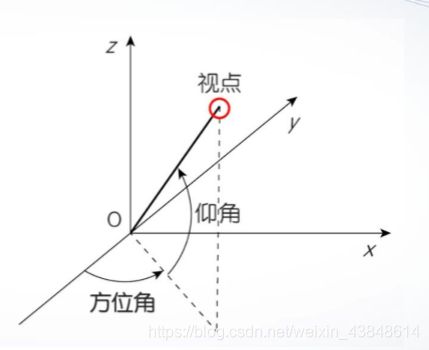
方位角az与仰角el为这样两个旋转角度：作一通过视点与z轴的平面，则该平面与x-y平面有一交线，该交线与y轴的反方向的、换逆时针方向(从z轴的方向观察）计算的、单位为度的夹角，就是观察点的方位角az；若角度为负值，则按顺时针方向计算。在通过视点与z轴的平面上，用一直线连接视点与坐标原点，该直线与x-y平面的夹角就是观察点的仰角el;若仰角为负值，则观察点转换到曲面下面：

https://blog.csdn.net/seamanj/article/details/35790359

（一）视点处理

 方位角：视点与原点连线在xy平面上的投影与y轴负方向形成的角度，正值表示逆时针，负值表示顺时针。
 仰角：视点与原点连线与xy平面的夹角，正值表示视点在xy平面上方，负值表示视点在xy平面下方。

（1）view函数的基本用法

view(az,el)
其中，az为方位角，el为仰角。系统默认的视点定义为
方位角-37.5°，仰角30°。

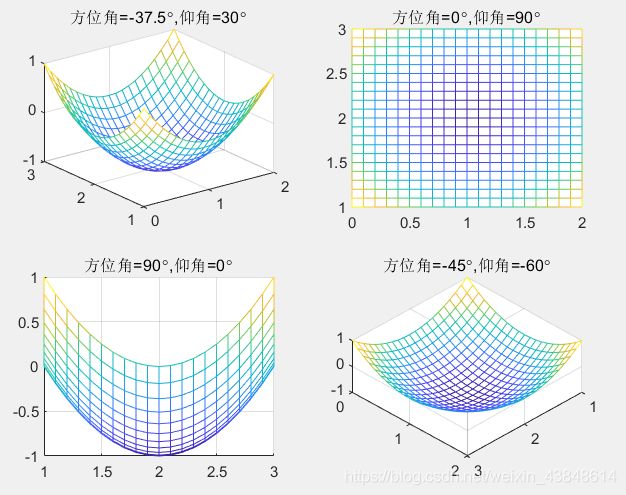
[x,y]=meshgrid(0:0.1:2, 1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1); mesh(x,y,z)
title('方位角=-37.5{\circ},仰角=30{\circ}')
subplot(2,2,2); mesh(x,y,z)
view(0,90);title('方位角=0{\circ},仰角=90{\circ}')
subplot(2,2,3); mesh(x,y,z)
view(90,0); title('方位角=90{\circ},仰角=0{\circ}')
subplot(2,2,4); mesh(x,y,z)
view(-45,-60); title('方位角=-45{\circ},仰角=-60{\circ}')

（2）view函数的其他用法

view(x,y,z) 视为 在笛卡尔坐标系中的位置
view(2)从二维平面观察图形，即方位角为0度，仰角为90度
view(3)从三维空间观察图形视点采用默认方位角和仰角

（二）色彩处理

（1）颜色的向量表示

向量元素在[0，1]范围内取值，3个元素依次表示红、绿、蓝3种颜色的
相对亮度，称为RGB三元组。

（2）色图（Colormap）

色图矩阵

cmap = colormap(parula(5)) 
cmap = 0.2081    0.1663    0.5292 
0.0795    0.5159    0.8328 
0.1986    0.7214    0.6310 
0.8266    0.7320    0.3464 
0.9763    0.9831    0.0538

指定当前图形使用的色图

colormap cmapname
colormap(cmap)

surf(peaks)
colormap hot

创建色图矩阵

色图矩阵的每一行是RGB三元组。可以自定义色图矩阵，也可以 调用MATLAB提供的函数来定义色图矩阵。

例2 创建一个灰色系列色图矩阵。

% cmap=gray(6);

c = [0, 0.2, 0.4, 0.6, 0.8, 1.0]';
cmap = [c, c, c]; 
surf(peaks) 
colormap(cmap)

三维图形表面的着色

用shading函数来改变着色方式。

例、使用同一色图，以不同着色方式绘制圆锥体。

[x,y,z]= cylinder(pi:-pi/5:0,10); 
colormap(lines); 
subplot(1,3,1); 
surf(x,y,z); 
shading flat subplot(1,3,2); 
surf(x,y,z); 
shading interp subplot(1,3,3); 
surf(x,y,z);

（三）、图形的裁剪处理

  将图形中需要裁剪部分对应的函数值设置成NaN，这样在绘制图形时，函数值为NaN的部分将不显示出来，从而达到对图形进行裁剪的目的。

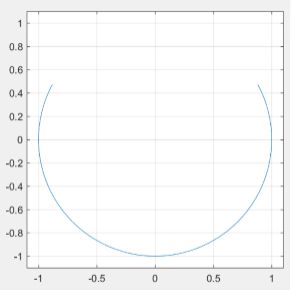
例、 绘制3/4圆

t = linspace(0,2*pi,100); 
x = sin(t); 
y = cos(t); 
p = y > 0.5; 
y(p)= NaN; 
plot(x,y) 
axis([-1.1,1.1,-1.1,1.1]) 
axis square 
grid on

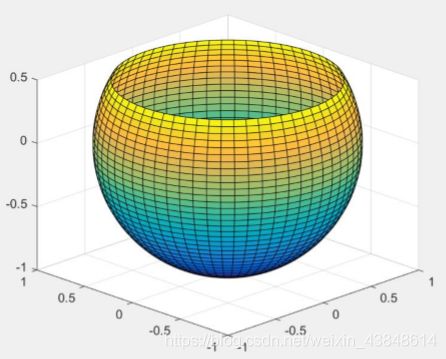
例、绘制3/4球面

[X, Y, Z] = sphere(60); 
p = Z>0.5; Z(p) = NaN; 
surf(X, Y, Z) 
axis([-1, 1, -1, 1, -1, 1]) 
axis equal 
view(-45, 20)

在选择多个变量时，要按住ctrl键，如我们同时选择d0av,d0sum两个变量，我们需要作出两个变量之间的对应关系的折线图

先选中的为横坐标，后选中的为纵坐标