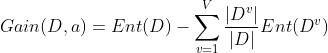机器学习-决策树（Decision Tree）基础篇

目录

一、决策树是什么

1-1、决策树学习基本算法

1-2、特征选择

1-3、信息熵

1-4、信息增益

二、决策树的构建

2-1、数据处理

2-2、信息熵的计算

2-3、决策树模型构建

2-4、决策树可视化

2-5、整体代码

---

一、决策树是什么

（1）决策树是一种基本的分类与回归方法。

（2）决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

（3）用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点， 最后将实例分到叶节点的类中。决策树是一种基本的分类与回归方法。

（4）决策树的的原理实际上可以由下图进行展示：

其中父节点和子节点是相对的，说白了子节点由父节点根据某一规则分裂而来，然后子节点作为新的父亲节点继续分裂，直至不能分裂为止。而根节点是没有父节点的节点，即初始分裂节点，叶子节点是 没有子节点的节点。

决策树利用如上图所示的树结构进行决策，每一个非叶子节点是一个判断条件，每一个叶子节点是结论。从跟节点开始，经过多次判断得出结论。

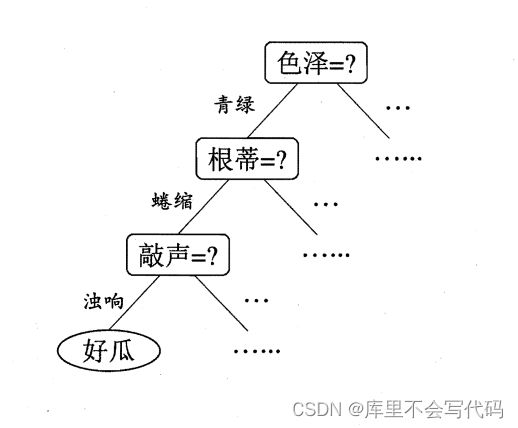
如果太过抽象，我们看一下西瓜书里的介绍，用西瓜举例来解释，通俗易懂！

我们要对“这是好瓜吗？”这样的问题进行决策时，通常会进行一系列的判断或“子决策”：我们先看“它是什么颜色？”，如果是“青绿色”，则我们再看“它的根蒂是什么形态？”，如果是“蜷缩”，我们再判断“它敲起来是什么声音？”，最后，我们得出最终决策：这是个好瓜。这个决策过程如下图所示。

1-1、决策树学习基本算法

决策树学习的目的是为了产生一颗泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单且直观的“分而治之”（divide-and-conquer）策略，如下图所示：

1-2、特征选择

由"分而治之"算法可看出，决策树学习的关键是第8行，即如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”越来越高。

1-3、信息熵

“信息熵”（information entrop）是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为（k=1,2,3,...,|y|），则D的信息熵定义为：

Ent(D)的值越小，则D的纯度越高。

1-4、信息增益

一般而言，“信息增益”（information gain）越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大。因此，我们可用信息增益来进行决策树的划分属性选择。信息增益定义为：

著名的ID3决策树学习算法就是以信息增益为准则来选择划分属性。

二、决策树的构建

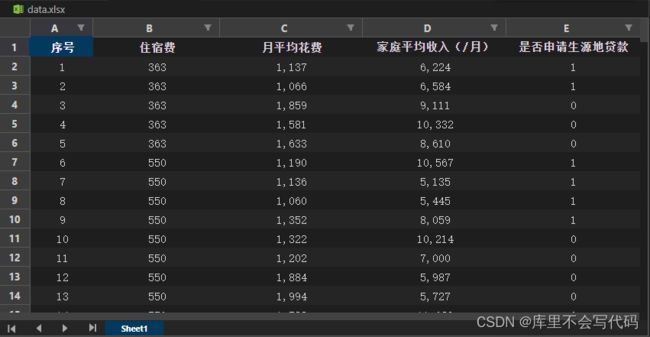
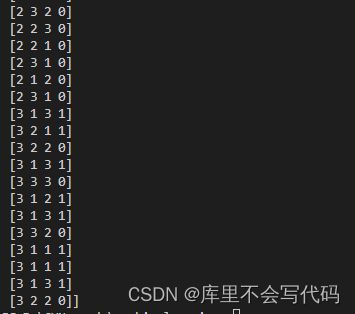
我们还拿之前kNN算法的数据集来做此篇博客，将住宿费、月平均花费、家庭平均收入(\月)作为数据集的特征，是否申请生源地贷款作为数据集的标签(为了方便算法，我们将0视为未申请生源地贷款，将1视为已申请生源地贷款)下图给出13条数据，实际数据共计77条。

2-1、数据处理

由于我们的数据集相对连续，如果直接拿来生成树，会非常的庞大，因此我们先对数据进行离散化。

对住宿费做如下处理：

300-800之间的设置为1，800-1200之间的设置为2，1200-1400之间的设置为3

对月平均花费做如下处理：

1000-1300之间的设置为1，1300-1600之间的设置为3，1600-2000之间的设置为3

对家庭平均收入做如下处理：

5000-8000之间的设置为1，8000-10000之间的设置为2，10000-12000之间的设置为3

这样就可以将数据集的每个属性规定为三种取值，即1或2或3

代码如下：

#数据离散化
def cut():
    #通过read_excel读取excel中的数据
    data = read_excel(data_path)
    #print(data[:,0])
    #print(data[:,1])
    #print(data[:,2])

    #使用pandas.cut实现对数据的离散化
    data[:,0] = pd.cut(data[:,0],[0,300,800,1200,1400],labels=False)
    data[:,1] = pd.cut(data[:,1],[0,1000,1300,1600,2000],labels=False)
    data[:,2] = pd.cut(data[:,2],[0,5000,8000,10000,12000],labels=False)
    #print(data)
    return data

对比数据离散化前后的效果，前三列对应的属性为["住宿费","月平均花费","家庭平均收入"]，最后一列为标签，即是否申请生源地贷款（0 or 1）

    

2-2、信息熵的计算

#计算给定数据集的香农熵
def calcShannonEnt(dataSet):
    #数据总个数
    totalNum = len(dataSet)
    #类别集合
    labelSet = {}
    #计算每个类别的样本个数
    for dataVec in dataSet:
        label = dataVec[-1]
        if label not in labelSet.keys():
            labelSet[label] = 0
        labelSet[label] += 1
    shannonEnt = 0
    #计算熵值
    for key in labelSet:
        pi = float(labelSet[key])/totalNum
        shannonEnt -= pi*math.log(pi,2)
    return shannonEnt

#print(dataset,'\n')
#print(dataLabels,'\n')
#print(calcShannonEnt(dataset))

#按给定特征划分数据集:返回第featNum个特征其值为value的样本集合，且返回的样本数据中已经去除该特征
def splitDataSet(dataSet, featNum, featvalue):
    retDataSet = []
    #numpy数据类型转为python列表
    if isinstance(dataSet,list) == False:
        dataSet = dataSet.tolist()
    for dataVec in dataSet:
        if dataVec[featNum] == featvalue:
            splitData = dataVec[:featNum]
            splitData.extend(dataVec[featNum+1:])
            retDataSet.append(splitData)
    return retDataSet

#选择最好的特征划分数据集
def chooseBestFeatToSplit(dataSet):
    featNum = len(dataSet[0]) - 1
    maxInfoGain = 0
    bestFeat = -1
    #计算样本熵值，对应公式中：H(X)
    baseShanno = calcShannonEnt(dataSet)
    #以每一个特征进行分类，找出使信息增益最大的特征
    for i in range(featNum):
        featList = [dataVec[i] for dataVec in dataSet]
        featList = set(featList)
        newShanno = 0
        #计算以第i个特征进行分类后的熵值，对应公式中：H(X|Y)
        for featValue in featList:
            subDataSet = splitDataSet(dataSet, i, featValue)
            prob = len(subDataSet)/float(len(dataSet))
            newShanno += prob*calcShannonEnt(subDataSet)
        #ID3算法：计算信息增益,对应公式中：g(X,Y)=H(X)-H(X|Y)
        infoGain = baseShanno - newShanno
        #C4.5算法：计算信息增益比
        #infoGain = (baseShanno - newShanno)/baseShanno
        #找出最大的熵值以及其对应的特征
        if infoGain > maxInfoGain:
            maxInfoGain = infoGain
            bestFeat = i
    return bestFeat

# 如果决策树递归生成完毕，且叶子节点中样本不是属于同一类，则以少数服从多数原则确定该叶子节点类别
def majorityCnt(labelList):
    labelSet = {}
    # 统计每个类别的样本个数
    for label in labelList:
        if label not in labelSet.keys():
            labelSet[label] = 0
        labelSet[label] += 1
    # iteritems：返回列表迭代器
    # operator.itemgeter(1):获取对象第一个域的值
    # True：降序
    sortedLabelSet = sorted(labelSet.items(), key=operator.itemgetter(1), reverse=True)
    return sortedLabelSet[0][0]

 离散后数据的香农熵计算结果为：

2-3、决策树模型构建

#创建决策树
def createDecideTree(dataSet, featName):
    #数据集的分类类别
    classList = [dataVec[-1] for dataVec in dataSet]
    #所有样本属于同一类时，停止划分，返回该类别
    if len(classList) == classList.count(classList[0]):
        return classList[0]
    #所有特征已经遍历完，停止划分，返回样本数最多的类别
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    #选择最好的特征进行划分
    bestFeat = chooseBestFeatToSplit(dataSet)
    beatFestName = featName[bestFeat]
    del featName[bestFeat]
    #以字典形式表示树
    DTree = {beatFestName:{}}
    #根据选择的特征，遍历该特征的所有属性值，在每个划分子集上递归调用createDecideTree
    featValue = [dataVec[bestFeat] for dataVec in dataSet]
    featValue = set(featValue)
    for value in featValue:
        subFeatName = featName[:]
        DTree[beatFestName][value] = createDecideTree(splitDataSet(dataSet,bestFeat,value), subFeatName)
    return DTree
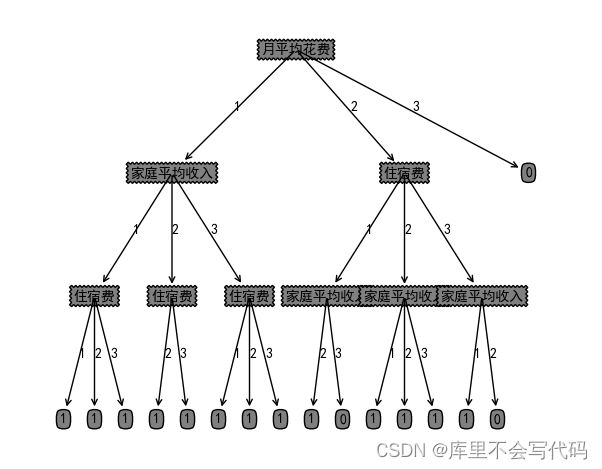
#print(createDecideTree(dataset,dataLabels))

输出打印构造的决策树，结果如下：

{'月平均花费': {1: {'家庭平均收入': {1: {'住宿费': {1: 1, 2: 1, 3: 1}}, 2: {'住宿费': {2: 1, 3: 1}}, 3: {'住宿费': {1: 1, 2: 1, 3: 1}}}}, 2: {'住宿费': {1: {'家庭平均收入': {2: 1, 3: 0}}, 2: {'家庭平均收入': {1: 1, 2: 1, 3: 1}}, 3: {'家庭平均收入': {1: 1, 2: 0}}}}, 3: 0}}

2-4、决策树可视化

我们通过Matplotlib来绘制决策树，使我们构造得决策树一目了然！

#获取叶节点的数目和树的层数
def getNumLeafs(tree):
    numLeafs = 0
    #获取第一个节点的分类特征
    firstFeat = list(tree.keys())[0]
    #得到firstFeat特征下的决策树（以字典方式表示）
    secondDict = tree[firstFeat]
    #遍历firstFeat下的每个节点
    for key in secondDict.keys():
        #如果节点类型为字典，说明该节点下仍然是一棵树，此时递归调用getNumLeafs
        if type(secondDict[key]).__name__== 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        #否则该节点为叶节点
        else:
            numLeafs += 1
    return numLeafs

#获取决策树深度
def getTreeDepth(tree):
    maxDepth = 0
    #获取第一个节点分类特征
    firstFeat = list(tree.keys())[0]
    #得到firstFeat特征下的决策树（以字典方式表示）
    secondDict = tree[firstFeat]
    #遍历firstFeat下的每个节点，返回子树中的最大深度
    for key in secondDict.keys():
        #如果节点类型为字典，说明该节点下仍然是一棵树，此时递归调用getTreeDepth，获取该子树深度
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


    #画出决策树
def createPlot(tree):
    # 定义一块画布，背景为白色
    fig = plt.figure(1, facecolor='white')
    # 清空画布
    fig.clf()
    # 不显示x、y轴刻度
    xyticks = dict(xticks=[], yticks=[])
    # frameon：是否绘制坐标轴矩形
    createPlot.pTree = plt.subplot(111, frameon=False, **xyticks)
    # 计算决策树叶子节点个数
    plotTree.totalW = float(getNumLeafs(tree))
    # 计算决策树深度
    plotTree.totalD = float(getTreeDepth(tree))
    # 最近绘制的叶子节点的x坐标
    plotTree.xOff = -0.5 / plotTree.totalW
    # 当前绘制的深度：y坐标
    plotTree.yOff = 1.0
    # （0.5,1.0）为根节点坐标
    plotTree(tree, (0.5, 1.0), '')
    plt.show()




# nodeText:要显示的文本；centerPt：文本中心点，即箭头所在的点；parentPt：指向文本的点；nodeType:节点属性
# ha='center'，va='center':水平、垂直方向中心对齐；bbox：方框属性
# arrowprops：箭头属性
# xycoords，textcoords选择坐标系；axes fraction-->0,0是轴域左下角，1,1是右上角
def plotNode(nodeText, centerPt, parentPt, nodeType):
    createPlot.pTree.annotate(nodeText, xy=parentPt, xycoords="axes fraction",
                              xytext=centerPt, textcoords='axes fraction',
                              va='center', ha='center', bbox=nodeType, arrowprops=arrow_args)

def plotMidText(centerPt, parentPt, midText):
    xMid = (parentPt[0] - centerPt[0]) / 2.0 + centerPt[0]
    yMid = (parentPt[1] - centerPt[1]) / 2.0 + centerPt[1]
    createPlot.pTree.text(xMid, yMid, midText)

def plotTree(tree, parentPt, nodeTxt):
    #计算叶子节点个数
    numLeafs = getNumLeafs(tree)
    #获取第一个节点特征
    firstFeat = list(tree.keys())[0]
    #计算当前节点的x坐标
    centerPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    #绘制当前节点
    plotMidText(centerPt,parentPt,nodeTxt)
    plotNode(firstFeat,centerPt,parentPt,decisionNode)
    secondDict = tree[firstFeat]
    #计算绘制深度
    plotTree.yOff -= 1.0/plotTree.totalD
    for key in secondDict.keys():
        #如果当前节点的子节点不是叶子节点，则递归
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key],centerPt,str(key))
        #如果当前节点的子节点是叶子节点，则绘制该叶节点
        else:
            #plotTree.xOff在绘制叶节点坐标的时候才会发生改变
            plotTree.xOff += 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff,plotTree.yOff),centerPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff),centerPt,str(key))
    plotTree.yOff += 1.0/plotTree.totalD

#createPlot(createDecideTree(dataset,dataLabels))

绘制结果如下：

2-5、整体代码

import math  #导入一系列数学函数和常量
import operator  #比较两个列表, 数字或字符串等的大小关系的函数
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *

# 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False

# 定义决策节点以及叶子节点属性：boxstyle表示文本框类型，sawtooth：锯齿形；fc表示边框线粗细
decisionNode = dict(boxstyle="sawtooth", fc="0.5")
leafNode = dict(boxstyle="round4", fc="0.5")
# 定义箭头属性
arrow_args = dict(arrowstyle="<-")

data_path = r'data.xlsx'

#读取数据集
def read_excel(path):
    raw_data = pd.read_excel(path,header=0)
    data = raw_data.values[:,1:5]
    return data

#数据离散化
def cut():
    #通过read_excel读取excel中的数据
    data = read_excel(data_path)
    #print(data[:,0])
    #print(data[:,1])
    #print(data[:,2])

    #使用pandas.cut实现对数据的离散化
    data[:,0] = pd.cut(data[:,0],[0,300,800,1200,1400],labels=False)
    data[:,1] = pd.cut(data[:,1],[0,1000,1300,1600,2000],labels=False)
    data[:,2] = pd.cut(data[:,2],[0,5000,8000,10000,12000],labels=False)
    #print(data)
    return data


#生成数据集
def createDataSet():
    dataSet = cut()
    labels = ["住宿费","月平均花费","家庭平均收入"]
    return dataSet,labels

dataset,dataLabels = createDataSet()


#计算给定数据集的香农熵
def calcShannonEnt(dataSet):
    #数据总个数
    totalNum = len(dataSet)
    #类别集合
    labelSet = {}
    #计算每个类别的样本个数
    for dataVec in dataSet:
        label = dataVec[-1]
        if label not in labelSet.keys():
            labelSet[label] = 0
        labelSet[label] += 1
    shannonEnt = 0
    #计算熵值
    for key in labelSet:
        pi = float(labelSet[key])/totalNum
        shannonEnt -= pi*math.log(pi,2)
    return shannonEnt

#print(dataset,'\n')
#print(dataLabels,'\n')
#print(calcShannonEnt(dataset))

#按给定特征划分数据集:返回第featNum个特征其值为value的样本集合，且返回的样本数据中已经去除该特征
def splitDataSet(dataSet, featNum, featvalue):
    retDataSet = []
    #numpy数据类型转为python列表
    if isinstance(dataSet,list) == False:
        dataSet = dataSet.tolist()
    for dataVec in dataSet:
        if dataVec[featNum] == featvalue:
            splitData = dataVec[:featNum]
            splitData.extend(dataVec[featNum+1:])
            retDataSet.append(splitData)
    return retDataSet

#选择最好的特征划分数据集
def chooseBestFeatToSplit(dataSet):
    featNum = len(dataSet[0]) - 1
    maxInfoGain = 0
    bestFeat = -1
    #计算样本熵值，对应公式中：H(X)
    baseShanno = calcShannonEnt(dataSet)
    #以每一个特征进行分类，找出使信息增益最大的特征
    for i in range(featNum):
        featList = [dataVec[i] for dataVec in dataSet]
        featList = set(featList)
        newShanno = 0
        #计算以第i个特征进行分类后的熵值，对应公式中：H(X|Y)
        for featValue in featList:
            subDataSet = splitDataSet(dataSet, i, featValue)
            prob = len(subDataSet)/float(len(dataSet))
            newShanno += prob*calcShannonEnt(subDataSet)
        #ID3算法：计算信息增益,对应公式中：g(X,Y)=H(X)-H(X|Y)
        infoGain = baseShanno - newShanno
        #C4.5算法：计算信息增益比
        #infoGain = (baseShanno - newShanno)/baseShanno
        #找出最大的熵值以及其对应的特征
        if infoGain > maxInfoGain:
            maxInfoGain = infoGain
            bestFeat = i
    return bestFeat

# 如果决策树递归生成完毕，且叶子节点中样本不是属于同一类，则以少数服从多数原则确定该叶子节点类别
def majorityCnt(labelList):
    labelSet = {}
    # 统计每个类别的样本个数
    for label in labelList:
        if label not in labelSet.keys():
            labelSet[label] = 0
        labelSet[label] += 1
    # iteritems：返回列表迭代器
    # operator.itemgeter(1):获取对象第一个域的值
    # True：降序
    sortedLabelSet = sorted(labelSet.items(), key=operator.itemgetter(1), reverse=True)
    return sortedLabelSet[0][0]

    '''
    



    '''
#创建决策树
def createDecideTree(dataSet, featName):
    #数据集的分类类别
    classList = [dataVec[-1] for dataVec in dataSet]
    #所有样本属于同一类时，停止划分，返回该类别
    if len(classList) == classList.count(classList[0]):
        return classList[0]
    #所有特征已经遍历完，停止划分，返回样本数最多的类别
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    #选择最好的特征进行划分
    bestFeat = chooseBestFeatToSplit(dataSet)
    beatFestName = featName[bestFeat]
    del featName[bestFeat]
    #以字典形式表示树
    DTree = {beatFestName:{}}
    #根据选择的特征，遍历该特征的所有属性值，在每个划分子集上递归调用createDecideTree
    featValue = [dataVec[bestFeat] for dataVec in dataSet]
    featValue = set(featValue)
    for value in featValue:
        subFeatName = featName[:]
        DTree[beatFestName][value] = createDecideTree(splitDataSet(dataSet,bestFeat,value), subFeatName)
    return DTree
print(createDecideTree(dataset,dataLabels))

'''
    
    
    
    
    
    
'''
#获取叶节点的数目和树的层数
def getNumLeafs(tree):
    numLeafs = 0
    #获取第一个节点的分类特征
    firstFeat = list(tree.keys())[0]
    #得到firstFeat特征下的决策树（以字典方式表示）
    secondDict = tree[firstFeat]
    #遍历firstFeat下的每个节点
    for key in secondDict.keys():
        #如果节点类型为字典，说明该节点下仍然是一棵树，此时递归调用getNumLeafs
        if type(secondDict[key]).__name__== 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        #否则该节点为叶节点
        else:
            numLeafs += 1
    return numLeafs

#获取决策树深度
def getTreeDepth(tree):
    maxDepth = 0
    #获取第一个节点分类特征
    firstFeat = list(tree.keys())[0]
    #得到firstFeat特征下的决策树（以字典方式表示）
    secondDict = tree[firstFeat]
    #遍历firstFeat下的每个节点，返回子树中的最大深度
    for key in secondDict.keys():
        #如果节点类型为字典，说明该节点下仍然是一棵树，此时递归调用getTreeDepth，获取该子树深度
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


    #画出决策树
def createPlot(tree):
    # 定义一块画布，背景为白色
    fig = plt.figure(1, facecolor='white')
    # 清空画布
    fig.clf()
    # 不显示x、y轴刻度
    xyticks = dict(xticks=[], yticks=[])
    # frameon：是否绘制坐标轴矩形
    createPlot.pTree = plt.subplot(111, frameon=False, **xyticks)
    # 计算决策树叶子节点个数
    plotTree.totalW = float(getNumLeafs(tree))
    # 计算决策树深度
    plotTree.totalD = float(getTreeDepth(tree))
    # 最近绘制的叶子节点的x坐标
    plotTree.xOff = -0.5 / plotTree.totalW
    # 当前绘制的深度：y坐标
    plotTree.yOff = 1.0
    # （0.5,1.0）为根节点坐标
    plotTree(tree, (0.5, 1.0), '')
    plt.show()




# nodeText:要显示的文本；centerPt：文本中心点，即箭头所在的点；parentPt：指向文本的点；nodeType:节点属性
# ha='center'，va='center':水平、垂直方向中心对齐；bbox：方框属性
# arrowprops：箭头属性
# xycoords，textcoords选择坐标系；axes fraction-->0,0是轴域左下角，1,1是右上角
def plotNode(nodeText, centerPt, parentPt, nodeType):
    createPlot.pTree.annotate(nodeText, xy=parentPt, xycoords="axes fraction",
                              xytext=centerPt, textcoords='axes fraction',
                              va='center', ha='center', bbox=nodeType, arrowprops=arrow_args)

def plotMidText(centerPt, parentPt, midText):
    xMid = (parentPt[0] - centerPt[0]) / 2.0 + centerPt[0]
    yMid = (parentPt[1] - centerPt[1]) / 2.0 + centerPt[1]
    createPlot.pTree.text(xMid, yMid, midText)

def plotTree(tree, parentPt, nodeTxt):
    #计算叶子节点个数
    numLeafs = getNumLeafs(tree)
    #获取第一个节点特征
    firstFeat = list(tree.keys())[0]
    #计算当前节点的x坐标
    centerPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    #绘制当前节点
    plotMidText(centerPt,parentPt,nodeTxt)
    plotNode(firstFeat,centerPt,parentPt,decisionNode)
    secondDict = tree[firstFeat]
    #计算绘制深度
    plotTree.yOff -= 1.0/plotTree.totalD
    for key in secondDict.keys():
        #如果当前节点的子节点不是叶子节点，则递归
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key],centerPt,str(key))
        #如果当前节点的子节点是叶子节点，则绘制该叶节点
        else:
            #plotTree.xOff在绘制叶节点坐标的时候才会发生改变
            plotTree.xOff += 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff,plotTree.yOff),centerPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff),centerPt,str(key))
    plotTree.yOff += 1.0/plotTree.totalD

createPlot(createDecideTree(dataset,dataLabels))