机器学习笔记之条件随机场(五)条件随机场需要解决的任务介绍

引言

上一节介绍了条件随机场的建模对象——条件概率$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$参数形式和向量形式的表示。本节将针对条件随机场面对的任务进行介绍。

回顾：条件随机场

条件随机场(Condition Random Field,CRF)是一种结合了最大熵模型(Maximum Entropy Model)和隐马尔可夫模型(Hidden Markov Model,HMM)特点的无向图模型。其概率图结构表示如下：

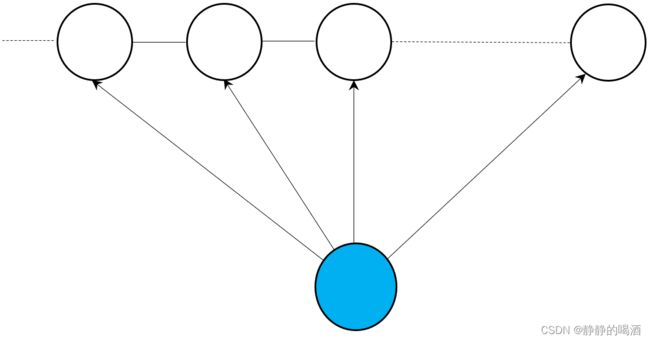
并且，它是一个概率判别模型，它的建模对象是关于隐变量的条件概率$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$：
$$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O})& =\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})+\sum _{t=1}^T\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})\right]\\ & =\frac{1}{\mathcal{Z}(\mathcal{O},\theta )}\exp ⟨\theta ,\mathcal{H}(i_{t+1},i_t,\mathcal{O})⟩\{\begin{array}{l}\theta =({\lambda }_1,\cdots ,{\lambda }_{\mathcal{M}},{\eta }_1,\cdots ,{\eta }_{\mathcal{L}}{)}^T\\ \mathcal{H}(i_{t+1},i_t,\mathcal{O})=\left(\begin{array}{c}{\sum }_{t=1}^{T-1}s(i_{t+1},i_t,\mathcal{O})\\ \\ {\sum }_{t-1}^{T}g(i_t,\mathcal{O})\end{array}\right)\end{array}\end{array}$$
并且，条件随机场打破了齐次马尔可夫假设和观测独立性假设，虽然没有脱离动态模型的范畴，但针对的目标是时间/序列状态转移过程有限的情况。例如：一条文本句子，一条蛋白质序列。

其中$s_m(i_{t+1},i_t,\mathcal{O})$被称作转移特征函数(Transition Feature Function)，$g_l(i_t,\mathcal{O})$被称作状态特征函数(State Feature Function)。以词性标注的角度为例，描述这两个特征函数。

• 一个句子由词语组成，这些词语的词性在句子中存在关联关系。例如：$\text{The boy knocked at the watermelon}$(男孩敲了敲西瓜)。

• 我们需要定义合适的特征函数，来刻画数据的一些可能成立或者期望成立的经验特性。

  当$t=3$时，此时的观测变量$o_3$为$\text{knocked}$，而下一时刻的词语是介词$\text{at}$。在条件随机场——背景介绍中提到特征函数通常是实值函数，因此当前时刻的状态特征函数$g_l(i_3,\mathcal{O})$表示如下：
  这里忽略‘时态’的影响，并且[$\mathcal{V}$]表示动词；[$\mathcal{P}$]表示介词。
  $$g_l(i_3,\mathcal{O})=\{\begin{array}{l}1\text{if }{i}_3=[\mathcal{V}]\text{ and }{o}_3{=}^{\prime }{\text{knock}}^{\prime }\\ 0\text{otherwise}\end{array}$$
  很明显，$i_3=[\mathcal{V}]\text{ and }{o}_3{=}^{\prime }{\text{knock}}^{\prime }$描述了一种既定事实，只要满足该事实条件，$g_l(i_3,\mathcal{O})$才有它的存在价值。同理，关于两个隐变量共同作用的转移特征函数$s_m(i_4,i_3,\mathcal{O})$表示如下：
  和状态特征函数类似，当“当前词语的词性是动词”且“下一个词语的词性是介词”，并且当前单词是$\text{knock}$时，该特征函数被启用。对应产生价值的大小由对应特征函数的参数${\lambda }_m,{\eta }_l$决定。
  $$s_m(i_4,i_3,\mathcal{O})=\{\begin{array}{l}1\text{if }{i}_4=[\mathcal{P}],i_3=[\mathcal{V}]\text{ and }{o}_3{=}^{\prime }{\text{knock}}^{\prime }\\ 0\text{otherwise}\end{array}$$

条件随机场要解决的任务

条件随机场作为一个概率图模型，其主要任务主要分为两个部分：

• 学习任务(Learning)，主要针对模型参数进行求解。(Parameter Estimation)
  对于条件随机场的学习任务，可以将其理解为：给定训练数据集$\mathcal{D}$：

  • 样本/标签维度均是$T$，即样本维度和条件随机场建模的‘序列/时间长度相同’。不要和‘转置符号’弄混;
  • 从真实样本的角度观察，样本$x^{(i)}$可能是某一个句子，一个序列，而不是一个单词，一个氨基酸;对应的标签$y^{(i)}$可能是‘每个单词的词性标注组成的序列’。
  • 各样本之间属于‘独立同分布’，各样本之间不存在关联关系。
    $$\begin{array}{rl}\mathcal{D}& =\{(x^{(i)},y^{(i)}){\}}_{i=1}^N{x}^{(i)},y^{(i)}\in {\mathbb{R}}^T\\ x^{(i)}& ={\left(x_1^{(i)},x_2^{(i)},\cdots ,x_T^{(i)}\right)}^T\to x_{1:T}^{(i)}\\ y^{(i)}& ={\left(y_1^{(i)},y_2^{(i)},\cdots ,y_T^{(i)}\right)}^T\end{array}$$

  对应图像示例如下：
  
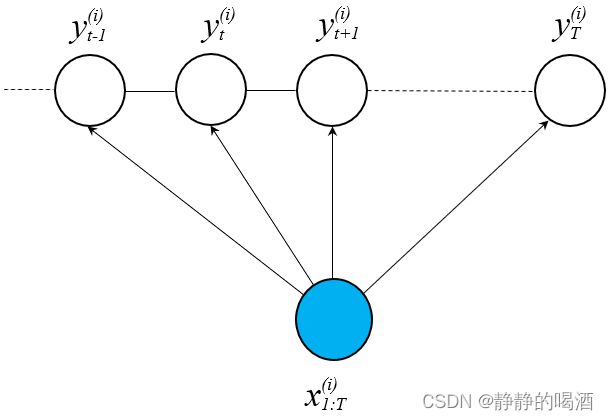
  对于最优参数$\hat{\theta }$的估计表示如下：
  其朴素思想在于：希望预测的标签序列$y$能够与对应的样本$x$最大程度的匹配，即$\mathcal{P}(y\mid x)$越大越好。并且各样本之间独立同分布，因此在学习过程中，模型参数的评价标准就是对‘数据集合内’的所有样本的$\mathcal{P}(y\mid x)$都达到最大。
  $$\begin{array}{r}\hat{\theta }=\underset{\theta }{\mathrm{argmax}}\prod _{i=1}^N\mathcal{P}\left(y^{(i)}\mid x^{(i)}\right)\end{array}$$

• 对于未知变量的推断任务(Inference)：
  在概率图模型——推断基本介绍中提到过关于推断的描述。

  • 通过联合概率分布，对边缘概率分布进行求解 (Marginal Probability)：
    $$\mathcal{P}(i_t\mid \mathcal{O})=\sum _{i_1,\cdots ,i_{t-1},i_{t+1},\cdots ,i_T}\mathcal{P}(\mathcal{I}\mid \mathcal{O})$$
    从样本角度观察，可以看作：给定一条完整句子序列的条件下，对句中某一单词词性的条件概率进行求解：
    $$\mathcal{P}(y_t^{(i)}\mid x_{1:T}^{(i)})$$
  • 求解条件概率分布(Conditional Probability)：
    $$\mathcal{I}={\mathcal{I}}_{\mathcal{A}}\cup {\mathcal{I}}_{\mathcal{B}}\to \mathcal{P}({\mathcal{I}}_{\mathcal{A}}\mid {\mathcal{I}}_{\mathcal{B}})$$
    由于条件随机场是概率判别模型，求解条件概率主要针对概率生成模型，对于概率判别模型基本没有意义。例如隐马尔可夫模型中的预测任务(Prediction)：
    齐次马尔可夫假设~
    $$\begin{array}{rl}\mathcal{P}(i_{t+1}\mid o_1,\cdots ,o_t)& =\sum _{i_t}\mathcal{P}(i_{t+1},i_t\mid o_1,\cdots ,o_t)\\ & =\sum _{i_t}\mathcal{P}(i_{t+1}\mid i_t,o_1,\cdots ,o_t)\cdot \mathcal{P}(i_t\mid o_1,\cdots ,o_t)\\ & =\sum _{i_t}\mathcal{P}(i_{t+1}\mid i_t)\cdot \mathcal{P}(i_t\mid o_1,\cdots ,o_t)\end{array}$$
    此时，将预测任务转化为滤波任务(Filtering)。对应概率图描述表示如下：
    
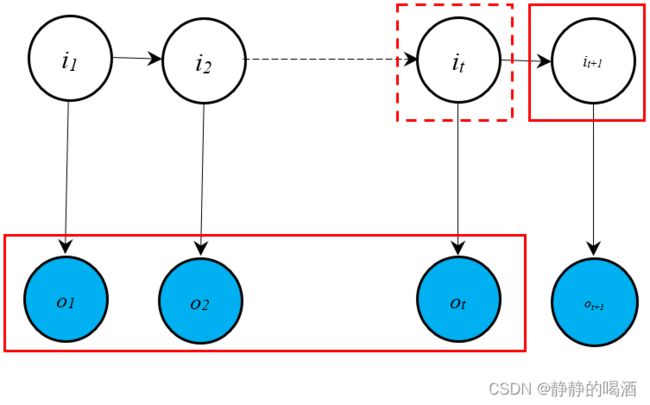
  • 最大后验概率推断(MAP Inference)：主要针对解码任务(Decoding)，依然以隐马尔可夫模型的解码任务为例，在求解$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\mathcal{P}(i_1,\cdots ,i_T\mid o_1,\cdots ,o_T)$过程中，需要求解一组适合的状态序列$\hat{\mathcal{I}}$，使得后验概率$\mathcal{P}(\hat{\mathcal{I}}\mid \mathcal{O},\lambda )$最大：
    $$\hat{\mathcal{I}}=\underset{\mathcal{I}}{\mathrm{argmax}}\mathcal{P}(\hat{\mathcal{I}}\mid \mathcal{O},\lambda )$$
    但实际求解过程并没有直接对$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$进行求解，而是通过 维特比算法 求解 相邻时刻下，状态变量取值的联合概率分布之间的关系：
    $$\begin{array}{rl}{\delta }_t(k)& =\underset{{\mathcal{I}}_{t-1}}{\max }\mathcal{P}(\mathcal{O},{\mathcal{I}}_{t-1},i_t=q_k\mid \lambda )\\ {\delta }_{t+1}(j)& =\underset{{\mathcal{I}}_t}{\max }\mathcal{P}(\mathcal{O},{\mathcal{I}}_t,i_{t+1}=q_j\mid \lambda )\\ {\delta }_t(k)& \stackrel{\text{?}}{\iff }{\delta }_{t+1}(j)\end{array}$$
    这种将$\mathcal{P}(\mathcal{I}\mid \mathcal{O},\lambda )$的问题转化为 $\mathcal{P}(\mathcal{I},\mathcal{O}\mid \lambda )$的问题，用到了最大后验概率(Maximum a posteriori Probability,MAP)的思想：
    $$\begin{array}{rl}\hat{\mathcal{I}}& =\underset{\mathcal{I}}{\mathrm{argmax}}\mathcal{P}(\mathcal{I}\mid \mathcal{O},\lambda )\\ & =\underset{\mathcal{I}}{\mathrm{argmax}}\frac{\mathcal{P}(\mathcal{I},\mathcal{O}\mid \lambda )}{\mathcal{P}(\mathcal{O},\lambda )}\\ & \propto \underset{\mathcal{I}}{\mathrm{argmax}}\mathcal{P}(\mathcal{I},\mathcal{O}\mid \lambda )\end{array}$$
    对于条件随机场，它的解码任务即：找到一条合适的词性标注序列$\hat{\mathcal{Y}}$，使得$\mathcal{P}(\hat{\mathcal{Y}}\mid \mathcal{X})$达到最大。其中$\mathcal{X}$表示一个句子样本。数学符号表达如下：
    $$\hat{\mathcal{Y}}=\underset{\mathcal{Y}=(y_1,\cdots ,y_T{)}^T}{\mathrm{argmax}}\mathcal{P}(\mathcal{Y}\mid \mathcal{X})$$

下一节将详细介绍条件随机场的推断任务。

相关参考：
机器学习-周志华著
机器学习-条件随机场（6）-CRF模型-要解决的问题