电信保温杯笔记——《统计学习方法(第二版)——李航》第11章 条件随机场
电信保温杯笔记——《统计学习方法(第二版)——李航》第11章 条件随机场
- 论文
- 介绍
- 概率无向图模型
-
- 图模型
- 马尔科夫性
-
- 成对马尔科夫性
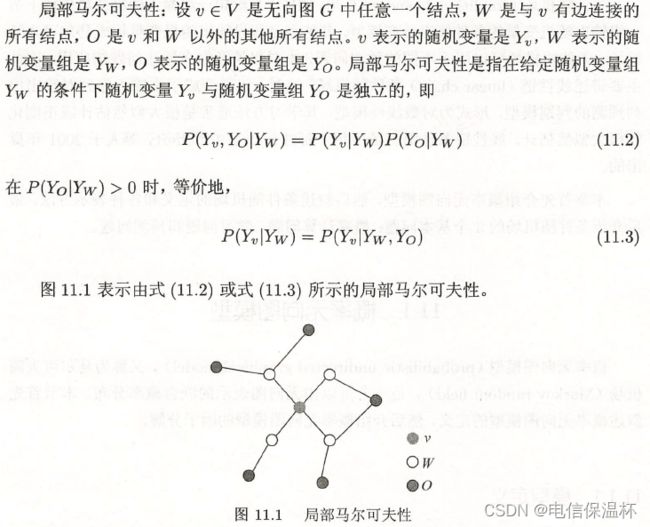
- 局部马尔科夫性
- 全局马尔科夫性
- 概率无向图的定义
- 概率无向图模型的因子分解
-
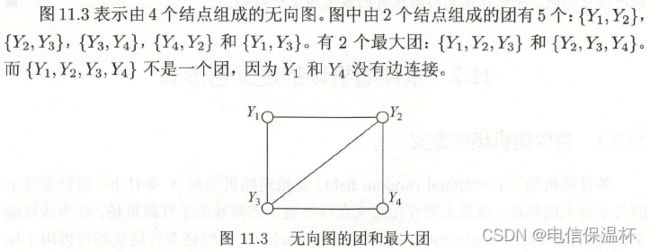
- 团与最大团
-
- 定义
- 例子
- 因子分解
- 条件随机场
-
- 条件随机场的定义
- 线性链条件随机场
- 条件随机场的形式
-
- 参数化形式
-
- 例子
- 简化形式
- 矩阵形式
-
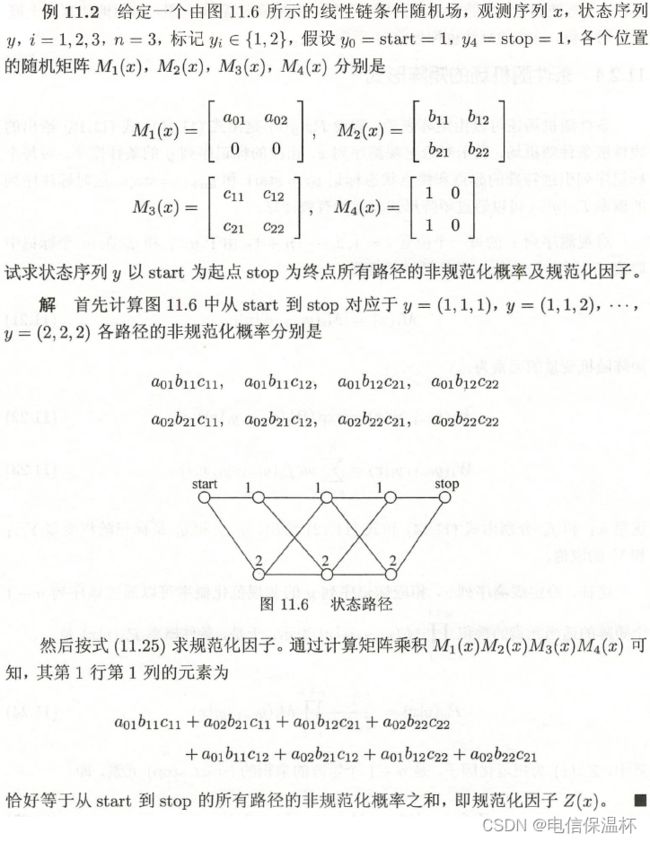
- 例子
- 条件随机场的概率计算
-
- 向前-向后算法
- 概率计算
- 期望计算
- 预测算法
-
- 步骤
- 例子
- 条件随机场的参数估计
-
- 改进的迭代尺度法
-
- 步骤
- 算法S
- 算法T
- 拟牛顿法
-
- 步骤
- 本章概要
- 备注
- 相关视频
- 相关的笔记
论文
CRF算法:《Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data》
介绍
电信保温杯笔记——《统计学习方法(第二版)——李航》
本文是对原书的精读,会有大量原书的截图,同时对书上不详尽的地方进行细致解读与改写。
条件随机场(conditional random field)是给定一组输入随机变量 X X X 条件下另一组输出随机变量 Y Y Y 的条件概率分布模型 P ( Y ∣ X ) P(Y|X) P(Y∣X),其特点是假设输出随机变量 Y Y Y 构成马尔可夫随机场。
马尔可夫随机场又称为概率无向图模型。故下面介绍概率无向图模型。
概率无向图模型
首先介绍图模型。
图模型
具有马尔科夫性的无向图,就是概率无向图,下面介绍马尔科夫性。
马尔科夫性
成对马尔科夫性
局部马尔科夫性
全局马尔科夫性
概率无向图的定义
概率无向图模型的因子分解
首先给出无向图中的团与最大团的定义。
团与最大团
定义
例子
因子分解
了解了马尔可夫随机场后,下面介绍条件随机场。条件随机场(conditional random field)是给定随机变量 X X X 条件下,随机变量 Y Y Y 的马尔可夫随机场。
条件随机场
条件随机场的定义
它想说的是, v v v 点状态的预测,只与跟它连接的节点的状态有关,与跟它没有连接的节点的状态无关,而隐马尔可夫模型的假设 v v v 点状态的预测只与它的前一个节点的状态有关,这是两者的不同之处。
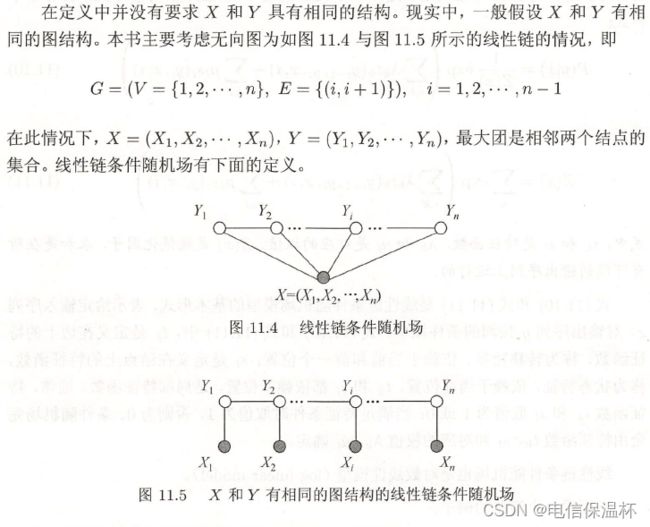
线性链条件随机场
它跟条件随机场的定义一致,只不过节点的结构变成了链表,故与条件随机场的定义中的节点 v v v 相连的节点只有前后2个。
条件随机场的形式
下面是条件随机场 P ( Y ∣ X ) P(Y|X) P(Y∣X) 公式化的各种表达形式。
参数化形式
就是条件概率写成 P ( Y ∣ X ) P(Y|X) P(Y∣X) 具体公式。

其中 y = ( y 1 , y 2 , ⋯ , y n ) y = (y_1, y_2, \cdots , y_n) y=(y1,y2,⋯,yn)。

例子
例子中 P ( y ∣ x ) = exp [ ∑ i = 1 n + 1 ( ∑ k = 1 5 λ k t k ( y i − 1 , y i , x , i ) + ∑ k = 1 4 μ k s k ( y i , x , i ) ) ] P(y | x) = \exp \left[ \sum\limits_{i = 1}^{n+1} \left( \sum\limits_{k = 1}^{5} \lambda_k t_k(y_{i-1} , y_i , x , i ) + \sum\limits_{k = 1}^{4} \mu_k s_k(y_i , x , i ) \right) \right] P(y∣x)=exp[i=1∑n+1(k=1∑5λktk(yi−1,yi,x,i)+k=1∑4μksk(yi,x,i))] 才与下文矩阵形式书写一致。
简化形式
矩阵形式
上式方括号是矩阵元素的表达式,即 A = [ a i j ] A = [a_{ij}] A=[aij]。
y i y_i yi 共有 m m m 个状态取值, i = 1 , ⋯ , n i = 1,\cdots , n i=1,⋯,n,所以矩阵是 m m m 阶的。因为 y 0 y_0 y0 和 y n + 1 y_{n+1} yn+1 只有一种取值,而矩阵 M 1 , M n + 1 M_1,M_{n+1} M1,Mn+1 又希望保持矩阵形式,故 M 1 M_1 M1 除第一行以外都是0, M n + 1 M_{n+1} Mn+1 除第一列以外都是0。

矩阵 [ M 1 ( x ) M 2 ( x ) ⋯ M n + 1 ( x ) ] [M_1(x)M_2(x) \cdots M_{n+1}(x)] [M1(x)M2(x)⋯Mn+1(x)] 只有左上角元素不为零。
例子
以上是模型的介绍,下面是模型的运用与参数估计方法。
条件随机场的概率计算
向前-向后算法
电信保温杯笔记——《统计学习方法(第二版)——李航》第10章 隐马尔可夫模型中有向前算法和向后算法的笔记。
概率计算
期望计算
预测算法
电信保温杯笔记——《统计学习方法(第二版)——李航》第10章 隐马尔可夫模型中有维特比算法的笔记。
步骤
例子
条件随机场的参数估计
改进的迭代尺度法
电信保温杯笔记——《统计学习方法(第二版)——李航》第6章 逻辑斯谛回归与最大熵模型中有关于改进的迭代尺度法的笔记。
步骤
算法S
算法T
拟牛顿法
步骤
本章概要
备注
求解的算法没有细看,但用的都是前几章的算法。
相关视频
相关的笔记
hktxt /Learn-Statistical-Learning-Method