OFDM雷达信号模糊函数MATLAB仿真分析

OFDM雷达信号模糊函数MATLAB仿真分析

OFDM大家都不陌生，特别是主要研究通信大法的小伙伴们。

正交频分复用 (OFDM) 是一种可以在多个正交子载波上编码通信数据的多载波调制方法，可以通过并行的低速子载波来实现高速数据传输。OFDM信号具有频谱效率高、能抵抗载波间干扰(ICI)和符号间干扰(ISI)、误码率小、可以通过IFFT/FFT实现调制/解调等诸多优点[1]。OFDM被 广泛应用于无线局域网 (WLAN)、第三/第四代移动通信和数字音频广播 (DAB) 系统[2]。另外，因为OFDM信号具有可以在高速移动条件下高速通信的优越性能，OFDM也被用于智能交通系统的波形设计[3]。

出于各种各样的原因，具体大家可以看一下相关的论文，目前很多雷达信号的研究也引入了OFDM信号。

这里也给大家分享一些笔者本人收集查阅过的资料哈。

链接：https://pan.baidu.com/s/1xrn0IeSTjbtyCM3ekqQOtg
提取码：h1hp
–来自百度网盘超级会员V2的分享

本文笔者主要是通过MATLAB仿真最基础的OFDM雷达信号，分析雷达信号的性能常用模糊函数这一工具，所以笔者的仿真目标是画出设定的OFDM雷达信号的模糊函数图像，希望能对大家有所帮助。

因为本文目标受众是和笔者一样的小白，所以前面花一定的篇幅简单介绍模糊函数等基本定义，比较熟悉的朋友(￣ω￣(￣ω￣〃 (￣ω￣〃)ゝ可以直接跳到最后的MATLAB仿真部分哈。

同时给大家准备一份小礼物(￣ω￣(￣ω￣〃 (￣ω￣〃)ゝ

https://download.csdn.net/download/qq_46084757/85521505

不要积分，分享本文中所有公式的word整理版本。大家可以直接插入自己的word里面使用。

模糊函数定义（熟悉这部分内容的小伙伴可以跳过）

在雷达系统中，为了使接收机的输出具有最大的信噪比，在雷达接收机前端通常首先使用匹配滤波器来对接收信号进行处理。因为在雷达信号的传输过程中，会引入时间延迟和多普勒频移，从而产生了信号失真[4]。为了分析在不同的时延和多普勒频移条件下接收信号与匹配滤波器的不匹配程度，定义了模糊度函数。

为了分析不同时延和多普勒频移条件下接收信号与匹配滤波器的失配，定义了模糊度函数。

在雷达系统中，为了使接收机的输出具有最大的信噪比，在雷达接收机前端通常首先使用匹配滤波器来对接收信号进行处理。因为在雷达信号的传输过程中，会引入时间延迟和多普勒频移，从而产生了信号失真[4]。为了分析在不同的时延和多普勒频移条件下接收信号与匹配滤波器的不匹配程度，定义了模糊度函数。

为了分析不同时延和多普勒频移条件下接收信号与匹配滤波器的失配，定义了模糊度函数。

OFDM雷达信号的模糊函数分析（熟悉这部分内容的小伙伴可以跳过）

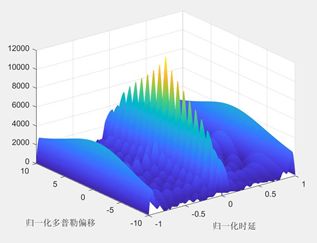
含有8个子载波的OFDM符号的模糊函数（多普勒偏移范围为[-10 10]）

继续分析：

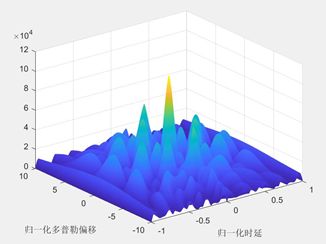
具有8个子载波、4个符号的多OFDM符号的模糊函数

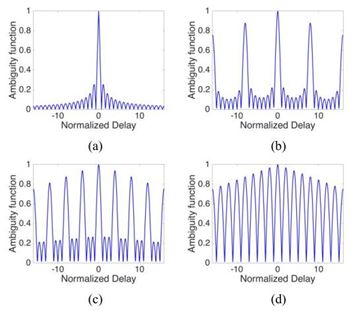
不同的M取值对应的距离模糊函数 (a) M=1, (b) M=2,© M=4,(d) M=8

由此可以初步推论：当OFDM雷达信号中的子载波越稀疏时，其距离模糊函数中的主瓣和栅瓣之间的间隔越窄，信号距离分辨力在栅瓣处比较差。

MATLAB仿真换出OFDM信号的模糊函数

核心代码

for j = 0:N_symbol - 1
    for k = 0:M-1
        for n = 0:N - 1
            x_source(k+1,n+1+j*N) = tx_data(k+1+j*N)*exp(1j*2*pi*k*n/N);%基带信号
        end
    end
end
for j = 1:M
    Source1(j,:) = (x_source(j,:).*exp(1j*2*pi*Fc*t));%发射信号
end
Source = sum(Source1);%发射信号 
% 如果 A 是矩阵，则 sum(A) 将返回包含每列总和的行向量。

%%计算传递函数 矩阵 
for j = 1:Na
    td = 2*R(j)/c;
    nd = ceil(td*Fs); % 该周期对应的 起始采样点数
    H(j,nd) = exp(-1j*2*pi*Fc*2*R(j)/c);
end

% figure;
% plot(abs(H(1,:)));

for j = 1:Na
    plot(abs(H(j,:)));
    hold on;
end



for i=1:Na
    Echo1(i,:) = ifft(fft(H(i,:)).*fft(Source));  %匹配滤波
    y(i,:) = ifft(fft(Echo1(i,:)).*conj(fft(Source)));%相参积累
end

mesh(abs(fft(y,[])))

完整MATLAB代码分享

完整MATLAB代码分享

https://download.csdn.net/download/qq_46084757/85521610