【现代密码学原理】——哈希函数（学习笔记）

前言：我们在登录QQ有时会遇到密码忘记的问题，那么思考一下，为什么腾讯公司不直接把密码发还给用户而是要求设置新密码呢。其实，不保存密码，是为了更好地对密码保密，换言之，腾讯的数据库根本没有存储你的密码。那腾讯又是怎么判断你的登录安全性呢，接下来的哈希函数就是其原理所在。

---

0. 思维导图

1. Hash函数

• Hash 函数，也称散列函数
• 可以将可变长度的数据块M 作为输入，产生一个固定长度的Hash值
  $\mathbf{h}=\mathbf{H}(\mathbf{M})$

“好”的Hash

• 对于较大的输入集合${\mathbf{M}}_1,{\mathbf{M}}_2,..{\mathbf{M}}_{\mathbf{n}}$,分别使用Hash函数进行处理，产生的输出结果${\mathbf{h}}_1,{\mathbf{h}}_2,..{\mathbf{h}}_{\mathbf{n}}$各元素的值是均匀分布、看起来随机的
• 换句话说，若数据块 任何一位或几位改变了，都将产生不同的Hash值，保证了数据完整性

密码学哈希函数
$\mathbf{h}=\mathbf{H}(\mathbf{M})，\mathbf{M}\ne {\mathbf{H}}^{-}(\mathbf{h})$
${\mathbf{h}}_1=\mathbf{H}({\mathbf{M}}_1)，{\mathbf{h}}_2=\mathbf{H}({\mathbf{M}}_2)$
${\mathbf{h}}_1\ne {\mathbf{h}}_2$

• 应用在网络安全中的Hash函数称为密码学Hash

• 已知Hash值，无法计算出对应的数据块——单向

• 数据块不同，生成的Hash值不同——抗碰撞

• 数据块M的长度为L位，在数据块M的后方增加填充内容P以及长度信息L
• 填充后的信息变为某固定长度的整数倍，便于Hash函数处理
• Hash函数读取填充后的信息，生成固定长度的Hash值

例子：

• 将Hash值 与消息M一起发送
• 攻击者将其截获，但不知道消息长度L，无法确认哪里是消息与填充内容的边界，提高了攻击者篡改消息的难度。

2. Hash函数的应用

2.1 消息认证

• 消息认证 是用来验证消息完整性的一种机制；
• 确保接收方Alice收到的数据确实和发送方Bob发出的数据一样，没有非授权的修改、插入、删除和重放；
• 消息认证 还要对发送方声称的身份进行认证；
• 当Hash 用于消息认证时，Hash值也称为消息摘要

2.1.1 使用哈希函数检查数据完整性

• Alice 要发送的消息为data，使用Hash函数计算出消息的Hash值 $H$
• 将$H$拼接到data的后面，一起发送给Bob
• Bob 接收后，从数据中将$n$位Hash值$H$提取出来
• 将剩余数据data’再次使用Hash函数进行计算
• 将得到的Hash值$H1$与接收到的$H$进行比较
• 二者不同，说明消息data或者传递的Hash值遭受了篡改

2.1.2 中间人攻击

• Alice 给 Bob 发送消息data，计算出Hash值为$H$，将$H$拼接在data后面，一起发送给Bob
• Darth 截获了该数据，并且他已知数据的最后$n$位为Hash值，因此截取出了原始明文消息data
• Darth 把原始消息篡改为data’，重新计算其Hash值，并附在data’后面一起转发给Bob
• Bob 收到篡改后的数据以及更新的Hash值，即使对消息data’进行Hash计算，也无法发现异常
• 为防止中间人攻击，Alice 对消息data 计算生成的Hash值必须得到保护

2.1.3 解决攻击的方案

方法一：消息$M$与哈希值$H(M)$均对称加密并传输

• A给B发送消息 ， 的Hash值为()，拼接得$\mathbf{M}\Vert \mathbf{H}(\mathbf{M})$
• 使用密钥 与 对称加密算法 为数据加密，生成$\mathbf{E}(\mathbf{K},\mathbf{M}\Vert \mathbf{H})$
• B 收到密文后，使用只有双方共享的密钥 解密，确认了消息一定来源于 A
• 解密得到$\mathbf{M}\Vert \mathbf{H}(\mathbf{M})$，再次使用Hash 对 进行计算，得到的值必然是()，确认了消息未被更改

Q：现在密钥K是绝对保密的，若攻击者截获了传输的数据，他能看到消息M 是什么吗？
A：不能

方法二：只对称加密哈希值并传输

• A给B发送消息 ， 的Hash值为()，加密得$\mathbf{E}(\mathbf{K},\mathbf{H}(\mathbf{M}))$
• 将加密后的Hash值 拼接在消息 后，一起发出$\mathbf{M}\Vert \mathbf{E}(\mathbf{K},\mathbf{H}(\mathbf{M}))$
• B 收到后，对后n位数据使用只有双方共享的密钥 解密，得到了Hash值，并且只有B 才能看到 Hash值
• 若对消息 进行计算得到的值与该Hash值相同，确认了消息未发生篡改

Q：现在密钥K是绝对保密的，若攻击者截获了传输的数据，并已知Hash值长度，那么他能看到消息M 是什么吗？
A：可以
Q：若攻击者截获了传输的数据并修改了M，他能否也篡改数据中的Hash值，使得接收方无法察觉？
A：不能

方法三：双方共享校验值

• 通信双方共享一个秘密值S
• A 将消息M 和秘密值S 串联后，计算其Hash值，并将得到的Hash值 附在消息M 后发送给B
• B 收到后，将双方预先知道的秘密值S 拼在M后，计算出Hash值，若与接收到的Hash值相同，说明消息未篡改
• 秘密值S 本身没有在信道中传送

Q：若攻击者截获了传输的数据，并已知Hash值的长度，他能否获取到消息M？
A：能
Q：若攻击者截获了传输的数据并修改了M，他能否也篡改数据中的Hash值，使得接收方无法察觉？
A：不能

方法四：消息$M$与哈希值$H(M)$均对称加密并加入校验值

• 在方案三的基础上，使用双方共享的密钥K与对称加密算法E 来为消息M 与Hash值H 一起加密
• 即保证了消息的保密性，也保证了完整性

2.2 数字签名

方法一：非对称加密哈希值并传输

• A给B发送消息 ， 的Hash值为()，加密得$\mathbf{E}(\mathbf{P}{\mathbf{R}}_{\mathbf{A}}，\mathbf{H}(\mathbf{M}))$，注意是发送方的私钥
• 将加密后的Hash值 拼接在消息 后，一起发出
• B 收到后，对消息 计算其Hash值
• 使用发送方A的公钥$\mathbf{P}{\mathbf{U}}_{\mathbf{A}}$ 来解密后半部分，得到了原始Hash值，若二者相同说明消息未被篡改

Q：若攻击者截获了传输的数据，并已知Hash值长度，他能否获取到消息M？
A：能
Q：若攻击者截获了传输的数据并修改了M，他能否也篡改数据中的Hash值，使得接收方无法察觉？
A：不能

方法二：

• 若既要保证消息的完整性，又要保证消息的保密性，可以在数字签名的基础上为 消息M 和 加密Hash值 一起使用密钥K 进行对称加密

Q：现在密钥K是绝对保密的，若攻击者截获了传输的数据，他能否获取到消息M？
A：不能

2.3 其他应用

2.3.1 存储口令

• Hash函数常被用于产生单向口令文件
• 即使黑客能够访问用户口令文件，看到的也只是口令的Hash值，无法得到真正的口令

2.3.1 安全检测

• Hash函数也可用于入侵检测或病毒检测
• 将每个文件的Hash值 H(F) 存储在安全系统中，通过定期重新计算H(F)，来判断文件是否被修改过

2.4 实际应用（了解）

• 比特币是于2008年发明的一种加密货币，并于2009年以其开源软件的形式发布。
• 它是一种分散（去中心化）的数字货币，无需中央银行或单一管理员。
  可以在对等比特币网络上从一个用户发送到另一个用户，而无需中介。
• 每个参与交易的人都拥有“账本” 。
• 在某个用户更新账本数据的时候，就要通知其他用户一起修改账本记录。
• 保密性：进行交易时使用收款人的公钥进行加密
• 认证性：进行交易时使用发款人的私钥进行身份认证
• 完整性：每个用户拥有的“账本”是交易记录，交易记录分成各个区块，每个区块用HASH函数进行HASH码的生成，并与其他区块链接到一起

3. 两个简单的Hash函数

3.1 XOR

• 若分组第一位始终为0，那么Hash的第一位也始终为0
• Hash 与明文统计规律相关，不安全

3.2 移位XOR

• 对当前Hash进行循环左移，消除同一经度的统计规律
• 使得 Hash值 更随机、更安全

思考：上面两个函数是真正的哈希函数吗？
答：哈希函数的一大特征：单向性，而异或是有办法逆向的

4. 密码学Hash函数的安全需求

1. 可变输入
   Hash函数 可应用于任意大小的数据块

2. 固定长度
   Hash函数 产生的是固定长度的输出

3. 计算效率
   对任意消息x，计算H(x)容易，硬件软件均可实现

4. 抗原像攻击
   对于Hash值 =() ，称是的原像
   给定，找到满足=() 的 在计算上不可行

5. 抗弱碰撞
   对任意给定的，找到满足≠ 且()=()的，在计算上不可行

6. 抗强碰撞
   找到任何满足()=()的偶对(,)，在计算上不可行

$\begin{array}{cccc}& \text{ 抗原像 }& \text{ 抗弱碰撞 }& \text{ 抗强碰撞 }\\ \text{ Hash数字签名 }& Y& Y& Y\\ \text{ 入侵检测、病毒检测 }& & Y& \\ \text{ 单向口令文件 }& Y& & \end{array}$

5. 攻击

5.1 穷举攻击

原像攻击、弱碰撞攻击

$$\begin{gathered} \mathbf{H}(\mathbf{y})=\mathbf{h} \\ {2}^{\mathbf{m}-1} \end{gathered}$$

• 对Hash函数发起穷举攻击，不依赖于任何算法细节，仅与 Hash值长度 有关
• 攻击者对给定的Hash值，随机选择并计算其Hash值，直到()= ，穷举规模，平均尝试⁻

碰撞攻击

$$\begin{gathered} \mathbf{H}(\mathbf{x})=\mathbf{H}(\mathbf{y}) \\ {2}^{\mathbf{m}/2} \end{gathered}$$

• 攻击者随机选择数据、，满足()=()
• 对于位的Hash值，预计在$\sqrt{2^m}=2^{m/2}$次尝试后就会出现碰撞

$$\begin{gathered} \mathbf{H}(\mathbf{x})=\mathbf{H}(\mathbf{y}) \\ {2}^{128/2} \end{gathered}$$

• $2^{\mathbf{m}/2}$决定了该Hash函数 抗穷举攻击 的强度
• Van Oosrschort等人斥巨资为128位的MD5设计了碰撞机，在24天内找到了一个碰撞

$$\begin{gathered} \mathbf{H}(\mathbf{x})=\mathbf{H}(\mathbf{y}) \\ {2}^{80} \end{gathered}$$

• 若 MD5值 变为160位，相同的碰撞机则需要4000年才可找出一个碰撞

• 而我国著名密码学家、中科院院士、2019未来科学大奖获得者、清华大学教授王小云 研究的MD5碰撞算法，将碰撞次数从$2^{80}$降低为$2^{69}$

强碰撞的应用——生日悖论

生日悖论 同一天生日的问题，反直觉概率， 同月同日生不是难事

生日悖论视频

步骤一

• 发送方A 准备对 消息x 进行签名
• 对消息x 进行Hash值计算，用A的私钥 对m位的 Hash值 加密，并将 加密的Hash值 附在 消息x 后

步骤二

• 攻击者产生消息 的$2^{\mathbf{m}/2}$ 种变式${\mathbf{x}}^{\prime }$，它们与表达相同的意义，将 所有${\mathbf{x}}^{\prime }$ 及其 Hash值 存储起来

步骤三

• 攻击者伪造消息 以及变式${\mathbf{y}}^{\prime }$，对每一个${\mathbf{y}}^{\prime }$ 计算 Hash值$\mathbf{H}({\mathbf{y}}^{\prime })$ ，并与$\mathbf{H}({\mathbf{x}}^{\prime })$ 进行对比，直到$\mathbf{H}({\mathbf{y}}^{\prime })=\mathbf{H}({\mathbf{x}}^{\prime })$

步骤四

• 攻击者将变式${\mathbf{x}}^{\prime }$ 提供给A 进行签名，将该签名附加在伪造的${\mathbf{y}}^{\prime }$之后发送给接收方
• 由于$\mathbf{H}({\mathbf{y}}^{\prime })=\mathbf{H}({\mathbf{x}}^{\prime })$ ，所以数字签名也是相同的

5.2 密码分析

• 对Hash函数发起密码分析攻击，依赖的是具体算法的设计缺点
• 典型Hash函数的总体结构如下所示，包括SHA在内的大多数Hash函数都是这种迭代结构

• 将输入消息分为$L$个固定长度的分组，每个分组长$b$位

• 最后一个分组不足$b$位，要加上填充内容$P$与消息长度

• Hash结构重复使用了函数

• 将第一个分组${\mathbf{Y}}_0$ 和 初始化变量$\mathbf{C}{\mathbf{V}}_0$ 输入到函数$f$中，输出一个$n$位分组$\mathbf{C}{\mathbf{V}}_1$

• 将下一个分组${\mathbf{Y}}_1$ 和 上一次输出$\mathbf{C}{\mathbf{V}}_1$ 输入到函数$f$中，输出一个$n$位分组$\mathbf{C}{\mathbf{V}}_2$

• 直到最后一个分组${\mathbf{Y}}_{\mathbf{L}-1}$ 和 上一次输出$\mathbf{C}{\mathbf{V}}_{\mathbf{L}-1}$ 输入到函数$f$中，输出最终的Hash值，即分组$\mathbf{C}{\mathbf{V}}_{\mathbf{L}}$

• 如果 迭代函数f 能够做到抗碰撞，那么Hash函数也会具有抗碰撞能力，密码分析就是分析$f$的内部结构

• 一个理想的Hash函数 要求密码分析所需的代价大于穷举攻击的代价

单选题：
原始消息的总长度是a位，将a位分成b位为一个分组，共L个分组。经过Hash函数的处理，输出Hash码为n位，问： Hash函数迭代结构中的初始值IV是多少位呢？
A.a B.b C.L D.n
答：选D

6. 安全Hash算法

• 安全Hash算法，简称SHA(Secure Hash Algorithm)，是使用最广泛的Hash函数，也是目前为止仅存的Hash算法标准
• SHA系列算法 由NIST设计，初始版本为SHA-0，于1993年作为联邦信息处理标准发布

• 随后SHA-0被发现存在安全缺陷，将其修订后变为SHA-1并于1995年发布

• SHA-1产生的是160位的Hash值

• SHA算法建立在MD4算法之上，基本框架与MD4相似

• 2002年，NIST又给出了三种新的SHA版本，Hash值长度依次为256、384、512位，统称为SHA-2

• SHA-2 的身影遍布在现今的各大Web应用之中
  

• Sony PS4 与游戏服务器通信的数据，使用AES-128加密、CBC工作模式、SHA-256完整校验

• XBOX ONE 与游戏服务器通信的数据，使用AES-256加密、CBC工作模式、SHA-384完整校验

• 2015年，NIST增加了两个算法SHA-512/224和SHA-512/256

• 我们将介绍SHA-2系列中的SHA-512，其他版本的算法与之类似

$\begin{array}{lllllll}& \text{ SHA-1 }& \text{ SHA-224 }& \text{ SHA-256 }& \text{ SHA-512 }& \begin{array}{l}\text{ SHA- }\\ 512/224\end{array}& \begin{array}{l}\text{ SHA- }\\ 512/256\end{array}\\ \text{ 消息摘要长度}& 160& 224& 256& 512& 224& 256\\ \text{ 消息长度 }& <2^{64}& <2^{64}& <2^{64}& <2^{128}& <2^{128}& <2^{128}\\ \text{ 分组长度 }& 512& 512& 512& 1024& 1024& 1024\\ \text{ 字长度 }& 32& 32& 32& 64& 64& 64\end{array}$

7. SHA-512

7.1 附加填充位（步骤1）

• 要处理消息，长度 bits
• 在消息后 增加 填充内容，使得填充后的长度${\mathbf{L}}_{\mathbf{M}}+{\mathbf{L}}_{\mathbf{P}}=896(\mathbf{m}\mathbf{o}\mathbf{d}1024)$
• 即使消息的长度已满足要求，仍需要进行填充
• 填充的位数在 1~1024 之间，填充内容为1和一串连续0

单选题：
关于SHA-512的说法正确的是？
A. SHA-512产生的摘要长度是512位
B. SHA-512要求对消息进行填充，填充部分的长度可以为0bit.
C. SHA-512还要求在消息的填充部分后加上256位的长度部分
D. SHA-512要求处理的分组长度是512位
答案：选A，摘要长度即哈希值长度；B错，不能为空；C错，是128位；D错，是1024位

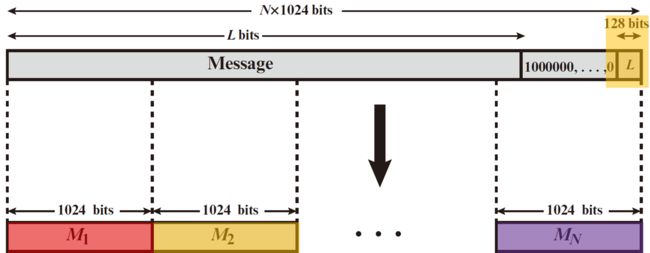
7.2 附加长度位（步骤2）

• 在填充内容 之后附加一个128位的块，用来放消息的长度
• 在该块中，将长度放在低位上，其余高位为空则放0
• 经过填充，消息长度为$N\ast 1024$，将其划分为一个个1024位的分组${\mathbf{M}}_1，{\mathbf{M}}_2，....{\mathbf{M}}_{\mathbf{N}}$

练习：
使用SHA-512算法，计算消息36的Hash值，问：
（1）消息长度是多少个bit？
（2）填充内容P 是什么？
（3）消息长度区域L 是什么？
答：
（1）$\mathbf{M}=36$，化二进制为：100100，因此消息的长度是6个bit
（2）${\mathbf{L}}_{\mathbf{M}}+{\mathbf{L}}_{\mathbf{P}}=896(\mathbf{m}\mathbf{o}\mathbf{d}1024)$
$6+{\mathbf{L}}_{\mathbf{P}}=896(\mathbf{m}\mathbf{o}\mathbf{d}1024)$
${\mathbf{L}}_{\mathbf{P}}=890(\mathbf{m}\mathbf{o}\mathbf{d}1024)=\mathbf{n}\times 1024+890$
令${\mathbf{L}}_{\mathbf{P}}=890$（即n取0），填充内容$\mathbf{P}$：1和889个0
（3）$\mathbf{M}=36$，继续填充 消息长度区域，消息长度为6，化为二进制110，将其放在 消息长度区域 的最低3位，其余高位填充为0，共128位
即消息长度区域为 125个0 和 110

7.3 缓冲区初始化（步骤3）

• Hash函数的 中间结果 和 最终结果 都保存在一个512位的缓存区中
• 512位缓存区 用8个64位的寄存器abcdefgh共同表示
• 将寄存器abcdefgh 进行初始化，对前8个素数开平方，取小数部分的前64位

7.4 分组处理（步骤4）

• SHA-512算法的核心是具有 80轮运算 的迭代函数F
• 用函数F依次处理各分组，最终的输出即为消息的Hash

7.5 迭代函数F

迭代函数$F$中的${\mathbf{W}}_0、{\mathbf{W}}_1\dots {\mathbf{W}}_{79}$是什么呢？

$\begin{array}{rl}{\sigma }_0^{512}(x)& ={\mathrm{ROTR}}^1(x)\oplus {\mathrm{ROTR}}^8(x)\oplus {\mathrm{SHR}}^7(x)\\ {\sigma }_1^{512}(x)& ={\mathrm{ROTR}}^{19}(x)\oplus {\mathrm{ROTR}}^{61}(x)\oplus {\mathrm{SHR}}^6(x)\end{array}$

• $\mathbf{R}\mathbf{O}\mathbf{T}{\mathbf{R}}^{\mathbf{n}}(\mathbf{x})$为对64位的变量$x$循环右移$n$位
• $\mathbf{S}\mathbf{H}{\mathbf{R}}^{\mathbf{n}}(\mathbf{x})$对64位的变量$x$右移$n$位，左边填充0

迭代函数$F$中的${\mathbf{K}}_0、{\mathbf{K}}_1\dots {\mathbf{K}}_{79}$又是什么呢？

${\mathbf{K}}_0、{\mathbf{K}}_1\dots {\mathbf{K}}_{79}$是轮常量

7.5.1 F中的轮函数R

$b、c、d、f、g、h$直接由$a、b、c、e、f、g$得到

$T_1=h+\mathrm{Ch}(e,f,g)+\left({\sum }_1^{512}e\right)+W_t+K_t$
$T_2=\left({\sum }_0^{512}a\right)+\mathrm{Maj}(a,b,c)$
$e=d+T_1$
$a=T_1+T_2$

其中：
$\text{ Ch }(e,f,g)=(\text{ e AND }f)⨁(\text{ NOT e AND g) }$
如果$e$则$f$，否则$g$

$\mathrm{Maj}(a,b,c)=(a\text{ AND b })⨁(a\text{ AND c })⨁(b\text{ AND c) }$
函数为真当且仅当变量的多数（2或3个）为真

$\left({\sum }_0^{512}a\right)={\mathrm{ROTR}}^{28}(a)⨁{\mathrm{ROTR}}^{34}(\mathrm{a})⨁{\mathrm{ROTR}}^{39}(\mathrm{a})$
$\left({\sum }_1^{512}e\right)={\mathrm{ROTR}}^{14}(\mathrm{e})⨁{\mathrm{ROTR}}^{18}(\mathrm{e})⨁{\mathrm{ROTR}}^{41}(\mathrm{e})$
$ROT{R}^n(x)$为对64位的变量$x$循环右移$n$位

单选题：
关于SHA-512的轮函数说法不正确的是？
A. 每个迭代函数包含了80轮的轮函数
B. 每个轮函数的输入有三部分，轮常量Kt，消息分组Mt和寄存器的值
C. 对于第一轮的轮函数，输入的是第一个消息分组的前32bit数据
D. 对于每轮轮函数，输出到寄存器b的值都是输入寄存器a的值
答案：选C，是64bit

8. SHA-512计算示例

$abc$
$979899$
$011000010110001001100011$

• 假设对三个ASCII字符“abc”进行Hash
• 首先将消息化为24位二进制比特串
• 消息长度L=24，消息要被填充为mod1024下与896同余，简单起见就取为896
• 故填充长度为896-24=872位，即1个“1”带着871个“0”

$6162638000000000000000000000000000000000000000000000000000000000$
$0000000000000000000000000000000000000000000000000000000000000000$
$0000000000000000000000000000000000000000000000000000000000000000$
$0000000000000000000000000000000000000000000000000000000000000018$

• 将填充内容1000…00拼接在消息后面，再将消息长度00…0011000 拼接在填充内容后面
• 构成的完整1024位消息分块的十六进制如上所示，分为16个64位字

$W_0=6162638000000000W_8=0000000000000000$
$W_1=0000000000000000W_9=0000000000000000$
$W_2=0000000000000000W_{10}=0000000000000000$
$W_3=0000000000000000W_{11}=0000000000000000$
$W_4=0000000000000000W_{12}=0000000000000000$
$W_5=0000000000000000W_{13}=0000000000000000$
$W_6=0000000000000000W_{14}=0000000000000000$
$W_7=0000000000000000W_{15}=0000000000000018$

• 在消息扩展过程中，该数据块的各个字被分别赋值给${\mathbf{W}}_0、{\mathbf{W}}_1、....{\mathbf{W}}_{15}$
• 而参与运算的其余${\mathbf{W}}_{16}、{\mathbf{W}}_{17}、...{\mathbf{W}}_{79}$可计算得到

$\begin{array}{cccl}a& 6a09e667f3bcc908& f6afceb8bcfcddf5& 1320f8c9fb872cc0\\ b& bb67ae8584caa73b& 6a09e667f3bcc908& f6afceb8bcfcddf5\\ c& 3c6ef372fe94f82b& bb67ae8584caa73b& 6a09e667f3bcc908\\ d& a54ff53a5f1d36f1& 3c6ef372fe94f82b& bb67ae8584caa73b\\ e& 510e527fade682d1& 58cb02347ab51f91& c3d4ebfd48650ffa\\ f& 9b05688c2b3e6c1f& 510e527fade682d1& 58cb02347ab51f91\\ g& 1f83d9abfb41bd6b& 9b05688c2b3e6c1f& 510e527fade682d1\\ h& 5be0cd19137e2179& 1f83d9abfb41bd6b& 9b05688c2b3e6c1f\end{array}$

• 8个寄存器$abcdefgh$的初始值为第一列，将其分别赋值给${\mathbf{H}}_{0,0}、{\mathbf{H}}_{0,1}、....{\mathbf{H}}_{0,7}$
• 右两列为经过两轮处理后的寄存器的值

$H_{1,0}=6a09e667f3bcc908+73a54f399fa4b1b2=ddaf35a193617aba$
$H_{1,1}=bb67ae8584caa73b+10d9c4c4295599f6=cc417349ae204131$
$H_{1,2}=3c6ef372fe94f82b+d67806db8b148677=12e6fa4e89a97ea2$
$H_{1,3}=a54ff53a5f1d36f1+654ef9abec389ca9=0a9eeee64b55d39a$
$H_{1,4}=510e527fade682d1+d08446aa79693ed7=2192992a274fc1a8$
$H_{1,5}=9b05688c2b3e6c1f+9bb4d39778c07f9e=36ba3c23a3feebbd$
$H_{1,6}=1f83d9abfb41bd6b+25c96a7768fb2aa3=454d4423643ce80e$
$H_{1,7}=5be0cd19137e2179+ceb9fc3691ce8326=2a9ac94fa54ca49f$

$ddaf35a193617abacc417349ae20413112e6fa4e89a97ea20a9eeee64b55d39a$
$2192992a274fc1a836ba3c23a3feebbd454d4423643ce80e2a9ac94fa54ca49f$

• 如上过程重复80轮后，最终得到512位的消息摘要

• 假设将输入消息改变1位，从“abc”变成“cbc”，对应的512位消息摘要发生了253位不同

$ddaf35a193617abacc417349ae20413112e6fa4e89a97ea20a9eeee64b55d39a$
$2192992a274fc1a836ba3c23a3feebbd454d4423643ce80e2a9ac94fa54ca49f$

• 即SHA-512 具有良好的雪崩效应

---

OK，以上就是本期知识点“哈希函数”的知识啦~~ ，感谢友友们的阅读。后续还会继续更新，欢迎持续关注哟~
如果有错误❌，欢迎批评指正呀~让我们一起相互进步
如果觉得收获满满，可以点点赞支持一下哟~