论文笔记:Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
前言
论文链接:https://www.aclweb.org/anthology/P19-1285/
github:https://github.com/kimiyoung/transformer-xl
目前在NLP领域中,处理语言建模问题有两种最先进的架构:RNN和Transformer。RNN按照序列顺序逐个学习输入的单词或字符之间的关系,而Transformer则接收一整段序列,然后使用self-attention机制来学习它们之间的依赖关系。这两种架构目前来看都取得了令人瞩目的成就,但它们都局限在捕捉长期依赖性上。
Transformer-XL是对Transformer的改进或变种,主要是解决长序列的问题,其中XL表示extra long,在最近流行的XLNet中就是使用Transformer-XL作为基础模块。
为了解决这一问题,CMU联合Google Brain在2019年1月推出的一篇新论文《Transformer-XL:Attentive Language Models beyond a Fixed-Length Context》同时结合了RNN序列建模和Transformer自注意力机制的优点,在输入数据的每个段上使用Transformer的注意力模块,并使用循环机制来学习连续段之间的依赖关系。Transformer-XL在多种语言建模数据集(如单词级别的enwik8和字符级别的text8)上实现了目前的SoTA效果,且该模型在推理阶段速度更快,比之前最先进的利用Transformer进行语言建模的方法快300~1800倍。
参考:
https://zhuanlan.zhihu.com/p/84159401
https://blog.csdn.net/magical_bubble/article/details/89060213
https://www.lyrn.ai/2019/01/16/transformer-xl-sota-language-model
1. Vanilla Transformer
transformer作为一种特征提取器,在NLP中有广泛的应用。但是transformer需要对输入序列设置一个固定的长度,比如在BERT中,默认长度是512。如果文本序列长度短于固定长度,可以通过填充的方式来解决。如果序列长度超过固定长度,处理起来就比较麻烦。一种处理方式,就是将文本划分为多个segments。训练的时候,对每个segment单独处理,segments之间没有联系,如下图(a)所示。这存在两个问题:
- 1)因为segments之间独立训练,所以不同的token之间,最长的依赖关系,就取决于segment的长度;
- 2)出于效率的考虑,在划分segments的时候,不考虑句子的自然边界,而是根据固定的长度来划分序列,导致分割出来的segments在语义上是不完整的。
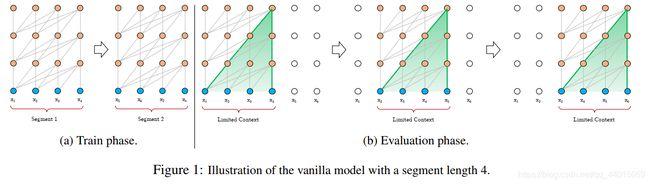
在预测的时候,会对固定长度的segment做计算,一般取最后一个位置的隐向量作为输出。为了充分利用上下文关系,在每做完一次预测之后,就对整个序列向右移动一个位置,再做一次计算,如上图(b)所示,这导致计算效率非常低。
2. Transformer-XL
Transformer-XL架构在vanilla Transformer的基础上引入了两点创新:循环机制(Recurrence Mechanism)和相对位置编码(Relative Positional Encoding),以克服vanilla Transformer的缺点。与vanilla Transformer相比,Transformer-XL的另一个优势是它可以被用于单词级和字符级的语言建模。
2.1 循环机制 Segment-Level Recurrence
与vanilla Transformer的基本思路一样,Transformer-XL仍然是使用分段的方式进行建模,但其与vanilla Transformer的本质不同是在于引入了段与段之间的循环机制,使得当前段在建模的时候能够利用之前段的信息来实现长期依赖性。如下图所示:
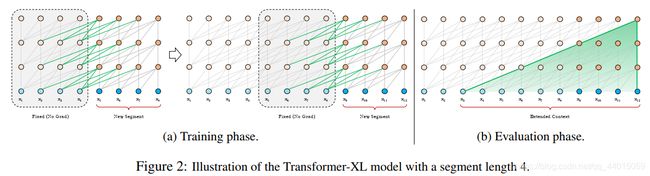
在对当前segment进行处理的时候,缓存并利用上一个segment中所有layer的隐向量序列,而且上一个segment的所有隐向量序列只参与前向计算,不再进行反向传播,这就是所谓的segment-level Recurrence。
在训练阶段,处理后面的段时,每个隐藏层都会接收两个输入:
- 该段的前面隐藏层的输出,与vanilla Transformer相同(上图的灰色线)。
- 前面段的隐藏层的输出(上图的绿色线),可以使模型创建长期依赖关系。
这两个输入会被拼接,然后用于计算当前段的Key和Value矩阵。对于某个段的某一层的具体计算公式如下:
h ~ T + 1 n − 1 = [ S G ( h T n − 1 ) ∘ h T + 1 n − 1 ] (extended context) \widetilde{h}_{\mathcal{T}+1}^{n-1}=[SG(h_{\mathcal{T}}^{n-1})\circ h_{\mathcal{T}+1}^{n-1}]\tag{extended context} h T+1n−1=[SG(hTn−1)∘hT+1n−1](extended context)
q T + 1 n , k T + 1 n , v T + 1 n = h T + 1 n − 1 W q T , h ~ T + 1 n − 1 W k T , h ~ T + 1 n − 1 W v T (query key,calue,vectors) q_{\mathcal{T+1}}^n,k_{\mathcal{T+1}}^n,v_{\mathcal{T+1}}^n=h_{\mathcal{T}+1}^{n-1}W_q^T,\widetilde{h}_{\mathcal{T}+1}^{n-1}W_k^T,\widetilde{h}_{\mathcal{T}+1}^{n-1}W_v^T \tag{query key,calue,vectors} qT+1n,kT+1n,vT+1n=hT+1n−1WqT,h T+1n−1WkT,h T+1n−1WvT(query key,calue,vectors)
h T + 1 n = T r a n s f o r m e r − L a y e r ( q T + 1 n , k T + 1 n , v T + 1 n ) (self-attention + feed-forward) h_{\mathcal{T}+1}^n=Transformer-Layer(q_{\mathcal{T}+1}^n,k_{\mathcal{T}+1}^n,v_{\mathcal{T}+1}^n) \tag{self-attention + feed-forward} hT+1n=Transformer−Layer(qT+1n,kT+1n,vT+1n)(self-attention + feed-forward)
其中, T \mathcal{T} T表示第几段, n n n表示第几层, h h h表示隐层的输出。 S G ( ∘ ) SG(\circ) SG(∘)表示停止计算梯度, [ h u ∘ h v ] [hu \circ hv] [hu∘hv]表示在长度维度上的两个隐层的拼接, W W W是模型参数。乍一看与Transformer中的计算公式很像,唯一关键的不同就在于Key和Value矩阵的计算上 k T + 1 n k_{\mathcal{T}+1}^n kT+1n和 v T + 1 n v_{\mathcal{T}+1}^n vT+1n,即它们基于的是扩展后的上下文隐层状态 h ~ T + 1 n − 1 \widetilde{h}_{\mathcal{T}+1}^{n-1} h T+1n−1进行计算, h T n − 1 h_{\mathcal{T}}^{n-1} hTn−1之前段的缓存。
原则上只要GPU内存允许,该方法可以利用前面更多段的信息,测试阶段也可以获得更长的依赖。
在测试阶段,与vanilla Transformer相比,其速度也会更快。在vanilla Transformer中,一次只能前进一个step,并且需要重新构建段,并全部从头开始计算;而在Transformer-XL中,每次可以前进一整个段,并利用之前段的数据来预测当前段的输出。
我们详细看一下如何操作。Transform本身是可以设置multi-heads,但是在后文中为了简化描述采用单个head。将两个连续的segments表示为 s T = [ x T , 1 , x T , 2 , . . . , x T , L ] s_{\mathcal{T}}=[x_{\mathcal{T},1},x_{\mathcal{T},2},...,x_{\mathcal{T},L}] sT=[xT,1,xT,2,...,xT,L], s T + 1 = [ x T + 1 , 1 , x T + 1 , 2 , . . . , x T + 1 , L ] s_{\mathcal{T}+1}=[x_{\mathcal{T}+1,1},x_{\mathcal{T}+1,2},...,x_{\mathcal{T}+1,L}] sT+1=[xT+1,1,xT+1,2,...,xT+1,L]。
L L L是序列长度。假设整个模型中,包含 N N N层Transformer,那么每个segment中就有 N N N组长度为 L L L的隐向量序列,
将第 T \mathcal{T} T个segment的第 n n n层隐向量序列表示为 h T n ∈ R L × d h_{\mathcal{T}}^n \in R^{L\times d} hTn∈RL×d, d d d是隐向量的维度.那么第 T + 1 \mathcal{T}+1 T+1 个segment的第n层隐向量序列可以由上述公式计算得出。 h ~ T + 1 n − 1 \widetilde{h}_{\mathcal{T}+1}^{n-1} h T+1n−1是对两个隐向量序列沿长度方向的拼接, [ ] [ ] []内两个隐向量的维度都是 L × d L \times d L×d,拼接之后的向量维度是 2 L × d 2L \times d 2L×d。3个 W W W分别对应query,key和value的转化矩阵。注意 q q q的计算方式不变,只使用当前segment中的隐向量,计算得到的 q q q序列长度仍然是 L L L。 k k k和 v v v采用拼接之后的 h ~ \widetilde{h} h 来计算,计算出来的序列长度是 2 L 2L 2L。之后的计算就是标准的Transformer计算。计算出来的第n层隐向量序列长度仍然是 L L L,而不是 2 L 2L 2L。Transformer的输出隐向量序列长度取决于query的序列长度,而不是key和value。
训练和预测过程如下图所示。这张图上有一个点需要注意,在当前segment中,第 n n n层的每个隐向量的计算,都是利用下一层中包括当前位置在内的,连续前 L L L个长度的隐向量,这是在上面的公式组中没有体现出来的,也是文中没有明说的。每一个位置的隐向量,除了自己的位置,都跟下一层中前 ( L − 1 ) (L-1) (L−1)个位置的token存在依赖关系,而且每往下走一层,依赖关系长度会增加 ( L − 1 ) (L-1) (L−1),如下图中Evaluation phase所示,所以最长的依赖关系长度是 N ( L − 1 ) N(L-1) N(L−1), N N N是模型中layer的数量。 N N N通常要比 L L L小很多,比如在BERT中, N = 12 N=12 N=12或者 N = 24 N=24 N=24, L = 512 L=512 L=512,依赖关系长度可以近似为 O ( N × L ) O(N \times L) O(N×L) 。在对长文本进行计算的时候,可以缓存上一个segment的隐向量的结果,不必重复计算,大幅提高计算效率。
上文中,我们只保存了上一个segment,实际操作的时候,可以保存尽可能多的segments,只要内存或者显存放得下。论文中的试验在训练的时候,只缓存一个segment,在预测的时候,会缓存多个segments。
2.2 相对位置编码 Relative Position Encodings
在Transformer中,一个重要的地方在于其考虑了序列的位置信息。在分段的情况下,如果仅仅对于每个段仍直接使用Transformer中的位置编码,即每个不同段在同一个位置上的表示使用相同的位置编码,就会出现问题。比如,第 i − 2 i−2 i−2段和第 i − 1 i−1 i−1段的第一个位置将具有相同的位置编码,但它们对于第ii段的建模重要性显然并不相同(例如第 i − 2 i−2 i−2段中的第一个位置重要性可能要低一些)。因此,需要对这种位置进行区分。
在vanilla Transformer中,为了表示序列中token的顺序关系,在模型的输入端,对每个token的输入embedding,加一个位置embedding。位置编码embedding或者采用正弦\余弦函数来生成,或者通过学习得到。在Transformer-XL中,这种方法行不通,每个segment都添加相同的位置编码,多个segments之间无法区分位置关系。Transformer-XL放弃使用绝对位置编码,而是采用相对位置编码,在计算当前位置隐向量的时候,考虑与之依赖token的相对位置关系。具体操作是,在算attention score的时候,只考虑query向量与key向量的相对位置关系,并且将这种相对位置关系,加入到每一层Trm的attention的计算中。
我们对两种方法做个对比。下面一组公式是vanilla Transformer计算attention的方式, E x E_x Ex 表示token的输入embedding, U U U是绝对位置编码embedding,两个 W W W分别是query矩阵和key矩阵。下面的公式是对 ( E x i + U i ) W q W k ( E x j + U j ) (E_{x_i}+U_i)W_qW_k(E_{x_j}+U_j) (Exi+Ui)WqWk(Exj+Uj) 做了分解。
A i , j a b s = E x i T W q T W k E x j ⏟ ( a ) + E x i T W q T W k U j ⏟ ( b ) + U i T W q T W k E x j ⏟ ( c ) + U i T W q T W k U j ⏟ ( d ) A_{i,j}^{abs}=\underbrace{E_{x_i}^TW_q^TW_kE_{x_j}}_{(a)}+\underbrace{E_{x_i}^TW_q^TW_kU_{j}}_{(b)}+\underbrace{U_{i}^TW_q^TW_kE_{x_j}}_{(c)}+\underbrace{U_{i}^TW_q^TW_kU_{j}}_{(d)} Ai,jabs=(a) ExiTWqTWkExj+(b) ExiTWqTWkUj+(c) UiTWqTWkExj+(d) UiTWqTWkUj
其中, E x i E_{x_i} Exi是词 i i i 的embedding, E x j E_{x_j} Exj 是词 j j j 的embedding, U i U_i Ui 和 U j U_j Uj 是位置向量,这个式子实际上是 ( W q ( E x i + U i ) ) T ⋅ ( W k ( E x j + U j ) ) (W_q(E_{x_i}+U_i))^T \cdot(W_k(E_{x_j}+U_j)) (Wq(Exi+Ui))T⋅(Wk(Exj+Uj))的展开,就是Transformer中的标准格式。
在Transformer-XL中,对上述的attention计算方式进行了变换,转为相对位置的计算,而且不仅仅在第一层这么计算,在每一层都是这样计算。
A i , j r e l = E x i T W q T W k , E E x j ⏟ ( a ) + E x i T W q T W k , R R i − j ⏟ ( b ) + u T W k , E E x j ⏟ ( c ) + v T W k , R R i − j ⏟ ( d ) A_{i,j}^{rel}=\underbrace{E_{x_i}^TW_q^TW_{k,E}E_{x_j}}_{(a)}+\underbrace{E_{x_i}^TW_q^TW_{k,R}\color{blue}{R_{i-j}}}_{(b)}+\underbrace{{\color{red}{u^T}}W_{k,E}E_{x_j}}_{(c)}+\underbrace{{\color{red}{v^T}}W_{k,R}\color{blue}{R_{i-j}}}_{(d)} Ai,jrel=(a) ExiTWqTWk,EExj+(b) ExiTWqTWk,RRi−j+(c) uTWk,EExj+(d) vTWk,RRi−j
对比来看,主要有三点变化:
- 在(b)和(d)这两项中,将所有绝对位置向量 U j U_j Uj都转为相对位置向量 R i − j R_{i−j} Ri−j,插一句,因为i只利用之前的序列,所以 i − j ≥ 0 i-j\geq 0 i−j≥0。与Transformer一样,这是一个固定的编码向量,不需要学习。相对位置关系用一个位置编码矩阵 R ∈ R L m a x × d R\in R^{L_{max}\times d} R∈RLmax×d,第 i i i行表示相对位置间隔为 i i i的位置向量。论文中强调 R R R采用正弦函数生成,而不是通过学习得到的,好处是预测时,可以使用比训练距离更长的位置向量。
- 在©这一项中,将查询的 U i T , W q T U_i^T,W_q^T UiT,WqT向量转为一个需要学习的参数向量 u ∈ R d u \in R^d u∈Rd,因为在考虑相对位置的时候,不需要查询的绝对位置 i i i,因此对于任意的 i i i,都可以采用同样的向量。同理,在(d)这一项中,也将查询的 U i T , W q T U_i^T,W_q^T UiT,WqT向量转为另一个需要学习的参数向量 v ∈ R d v \in R^d v∈Rd。
- 将键的权重变换矩阵 W k W_k Wk转为 W k , E W_{k,E} Wk,E和 W k , R W_{k,R} Wk,R,分别作为content-based key vectors和location-based key vectors。
从另一个角度来解读这个公式的话,可以将attention的计算分为如下四个部分:
- a. 基于内容的“寻址”,即没有添加原始位置编码的原始分数。
- b. 基于内容的位置偏置,即相对于当前内容的位置偏差。
- c. 全局的内容偏置,用于衡量key的重要性。
- d. 全局的位置偏置,根据query和key之间的距离调整重要性。
2.3 计算公式及矩阵形式
结合上面两个创新点,将Transformer-XL模型的整体计算公式整理如下,这里考虑一个N层的只有一个注意力头的模型:

其中, T \mathcal{T} T代表第几段, n n n 代表第几层, h T 0 : = E s T h_{\mathcal{T}}^0:=E_{s_{\mathcal{T}}} hT0:=EsT定义为第 T \mathcal{T} T段的词向量序列。值得一提的是,计算 A A A矩阵的时候,需要对所有的 i − j i−j i−j计算 W k , R n W^n_{k,R} Wk,Rn, R i − j R_{i−j} Ri−j,如果直接按照公式计算的话,计算时间是 O ( l e n g t h ) 2 O(length)^2 O(length)2,而实际上 i − j i−j i−j的范围只从 0 l e n g t h 0 ~ length 0 length,因此可以先计算好这 l e n g t h length length个向量,然后在实际计算 A A A矩阵时直接取用即可。
具体的,设 M M M和 L L L分别为memory和当前段序列的长度,则 i − j i−j i−j的范围也就为 0 M + L − 1 0 ~ M+L−1 0 M+L−1。下面的 Q Q Q矩阵中的每一行都代表着 W k , R W_{k,R} Wk,R, R i − j R_{i−j} Ri−j中一个 i − j i−j i−j的可能性,即 Q k = W k , R R M + L − 1 − k Q_k=W_{k,R}R_{M+L-1-k} Qk=Wk,RRM+L−1−k 。
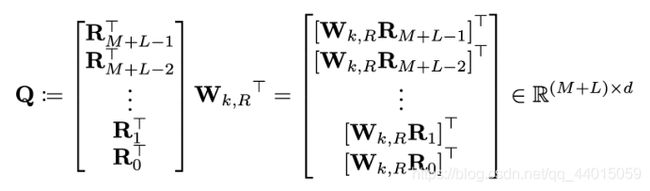
则对于上面公式中的(b)项,即 q i T W k , R R i − j q_i^T W_{k,R}R_{i-j} qiTWk,RRi−j,其构成的所有可能向量的矩阵为 B B B矩阵,其形状为 L ∗ ( M + L ) L\ast (M+L) L∗(M+L),这是我们最终需要的(b)项的attention结果。
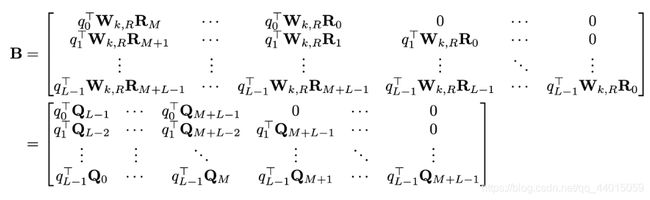
我们进一步定义 B ~ \widetilde{B} B 矩阵为如下:
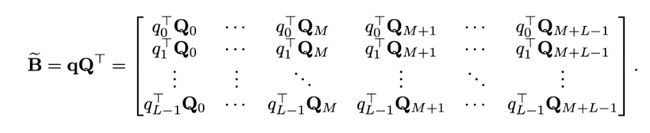
可见,需要的BB矩阵的每一行只是 B ~ \widetilde{B} B 的向左shift而已。因此,可以直接利用矩阵乘法计算 B ~ \widetilde{B} B 即可。设 R i − j R_{i-j} Ri−j的维度为 d R d_R dR, q i q_i qi的维度为 d q d_q dq, W k , R W_{k,R} Wk,R矩阵的维度为 d q ∗ d R d_q\ast d_R dq∗dR则直接计算矩阵B的时间复杂度为 2 ∗ d q ∗ d R ∗ L ∗ ( M + L ) 2∗d_q∗d_R∗L∗(M+L) 2∗dq∗dR∗L∗(M+L),而计算 B ~ \widetilde{B} B 的时间复杂度为 L ∗ d q ∗ ( M + L ) + d q ∗ d R ∗ ( M + L ) L∗d_q∗(M+L)+d_q∗d_R∗(M+L) L∗dq∗(M+L)+dq∗dR∗(M+L)计算量明显不是一个量级(后者要快很多)。
同理,对于(d)项来说,可以对所有的 i − j i−j i−j定义需要的矩阵 D D D 为 L ∗ ( M + L ) L ∗ ( M + L ) L∗(M+L)L∗(M+L) L∗(M+L)L∗(M+L):
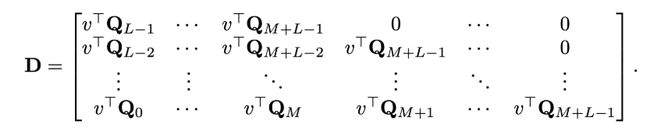
可以用如下的 d ~ \widetilde{d} d 来进行shift得到:
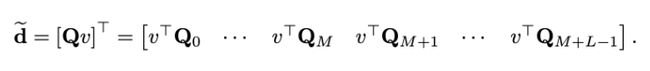
其中 Q Q Q矩阵已经计算过了,也可以在这一步减少计算量。
3. 实验
3.1 语言建模指标
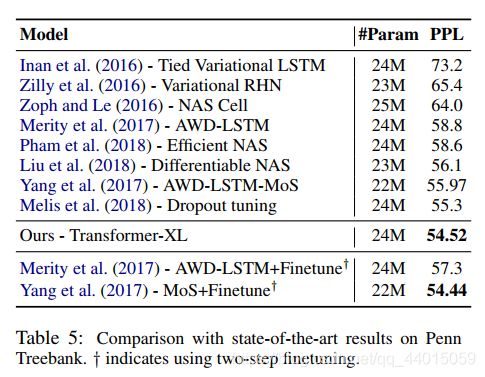
在最关心的语言模型建模指标上,论文比较了模型在单词级别和字符级别上不同数据集的表现,并且与RNN和(vanilla) Transformer都做了比较。实验证明,Transformer-XL在各个不同的数据集上均实现了目前的SoTA:在大型单词级别数据集WikiText-103上,Transformer-XL将困惑度从20.5降到18.3;在enwiki8数据集上,12层Transformer-XL的bpc达到了1.06,相同bpc的AI-Rfou的模型参数量却是6倍,24层Transformer-XL的bpc更是达到了0.99;在One Billion Word数据集上(仅具有短句的)和Penn Treebank数据集上(小型,仅有1M)也取得了SoTA的效果,前者的困惑度从23.7到21.8,后者的困惑度从55.3到54.5。表明了Transformer-XL在各个数据集下的不俗竞争力。
3.2 两个创新点的优势
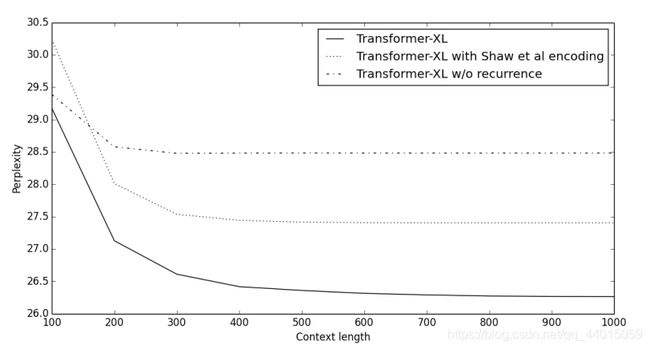
下图比较了不同上下文长度(即memory的长度)中包不包含循环机制、以及使不使用新位置编码方式的困惑度得分。可见,使用循环机制和相对位置编码的Transformer-XL明显优于其他的模型,并且能够有效利用长期依赖性,而且它能捕获超出RNN 80%的依赖性,和超出Transformer 450%的依赖性。
3.3 测试阶段的速度
Transformer-XL的推理速度也明显快于vanilla Transformer,尤其是对于较长的上下文。比如,在上下文长度为800时,Transformer-XL提速363倍;而当上下文长度增加到3800时,Transformer-XL提速1874倍!
4. 总结
4.1 模型特点
- 引入循环机制(Recurrence Mechanism)
- 相对位置编码(Relative Positional Encoding)
4.2 优点
- 在几种不同的数据集(大/小,字符级别/单词级别等)均实现了最先进的语言建模结果。
- 结合了深度学习的两个重要概念——循环机制和注意力机制,允许模型学习长期依赖性,且可能可以扩展到需要该能力的其他深度学习领域,例如音频分析(如每秒16k样本的语音数据)等。
- 在inference阶段非常快,比之前最先进的利用Transformer模型进行语言建模的方法快300~1800倍。
- 有详尽的源码!含TensorFlow和PyTorch版本的,并且有TensorFlow预训练好的模型及各个数据集上详尽的超参数设置。
4.3 不足
- 尚未在具体的NLP任务如情感分析、QA等上应用。
- 没有给出与其他的基于Transformer的模型,如BERT等,对比有何优势。
- 在Github源码中提到,目前的sota结果是在TPU大集群上训练得出,对于我等渣机器党就只能玩玩base模式了。