机器学习--朴素贝叶斯(Naive Bayes)
概率图模型:
概率图,概率和图的相结合,那么它构建了一副什么样的图呢?
用观测点表示观测到的数据,隐含点表示潜在的知识,用边来描述知识和数据之间的相互关系,最后基于一个这样的关系图,获得一个概率分布。
概率图的节点分为观测节点和隐含节点,边分为有向边和无向边,节点呢就代表随机变量,边代表随机变量的相关关系,其中有向边表示单向依赖,无向边表示双向的依赖。
概率图模型主要分为两类:
贝叶斯网络,马尔可夫网络
区别:贝叶斯网络可以用有向图结构表示,而马尔可夫网络可以表示一个无向图表示
准确的来说:概率图模型包括了朴素贝叶斯,最大熵模型,隐马尔可夫模型,条件随机场模型,主题模型等等。
首先会了这三个公式这节课就全会了,下面三个是三个公理,注意不是定理,什么是公理?
就是这个定义是不存在的,我们假设他是正确的,然后需要我们是有个定理去证明它确实是正确的。
1.0<=p(A)<=1
2.p(True) = 1 , p(False) = 0
3.p(A) + p(B) - p(A and B) = p(A or B)
P(A|B) = P(A,B)/P(B) 这个公式也就是说B条件发生的情况下,A条件的概率
P(A,B) = P(A|B)*P(B) 这个公式代表的是说A和B的联合概率就等于B的条件概率乘以B的概率
求P(a,b,c)=?
P(a|b,c)*P(b|c)*P(c)
P(A|B) = P(A) if A⊥B
P(A,B) = P(A) * P(B)
贝叶斯模型,也是属于概率图模型的,属于有向图模型
那么这里边的动机是什么呢?
比如有N个变量X1,X2.......Xn
如果知道x1到xn的联合分布P(X1....Xn)那么我们就可以回答任何问题
比如说我们就会知道P(Xi)的概率,也可以知道P(Xi|Xj)的概率,那么我们最终的目的就是想知道这个联合分布,那么但是如果我们通过对每个概率进行计算然后建模的话,复杂度会特别的高,因此呢需要找到一种有效的更好的方式对模型进行建模。
例子:为什么会时间复杂度很高
那么概率图模型就是想解决这个问题,那么具体他是怎么解决的呢
就是说有没有一种可能,假设变量之间存在某种关系,比如说:x1的取值取决于x2,x2又取决于x3,x1又取决于x3。以一种图的形式来对它进行建模,这种图就是有向无环图。
举例:
那么概率图模型有什么样的好处?
可以将储存空间瞬间以指数形式降低。
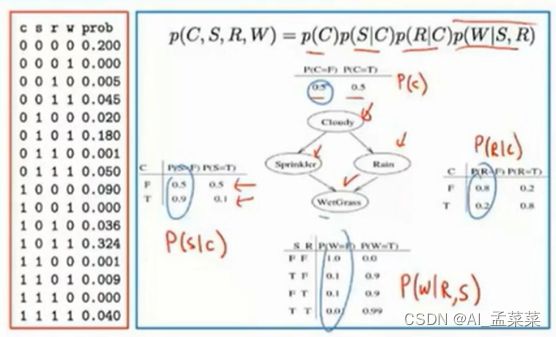
那么现在知道了贝叶斯网络之后,同样最终的应用是不是仍然实在求解问题上,比如说
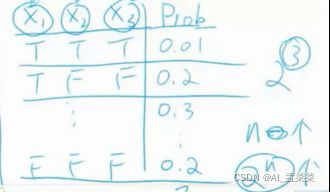
要求p(s=1)的概率,那么使用最最笨的方法就是,查左边的表,然后将s=1的情况全部加起来除以1,这个是很麻烦的为什么这么说呢,因为这必须站在上帝视角去看这件事情,因为现实生活中表肯定不会是最全的,然后还需要对表后边的一个概率进行一个计算:
然后我们说这样算是比较麻烦的因此来说呢,就使用下边的方式对上述的全概率进行展开,这样是不是就由原来的15项,变成了现在的9项。
怎么求?硬求:
但是还有点麻烦,这时候再去优化,动态优化。
朴素贝叶斯
其实朴素贝叶斯就是概率图模型
朴素贝叶斯就是简单的概率图模型,原理就是利用贝叶斯公式当中,根据某特征的先验概率,计算其后验概率,然后选择后验概率得到所属的类。
朴素贝叶斯又做了一个假设,就是说假设每个特征之间都是相互独立的,那么P(联合分布)=p1*p2.......pn。
接着先看一下全概率公式:
这时候结合前边公式看一下:
P(A):就是先验概率,在B事件发生之前,我们对A事件进行了一个统计判断。
P(A|B):就是后验概率,在B事件发生之后,我们对A事件进行了重新的评估。