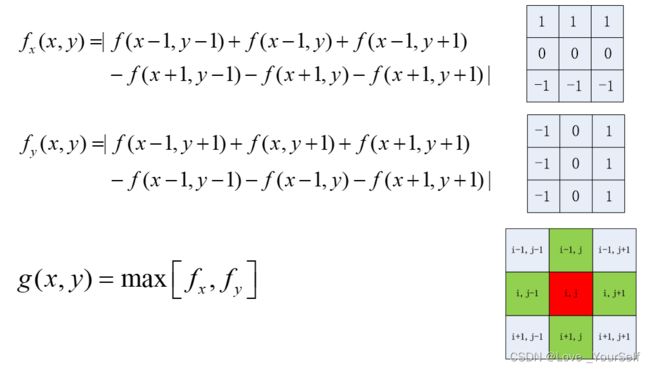python进行图像边缘检测

边缘检测

图像边缘是指图像中表达物体的周围像素灰度发生阶跃变化的那些像素集合。
图像中两个灰度不同的相邻区域的交界处，必然存在灰度的快速过渡或称为跳变，它们与图像中各区域边缘的位置相对应，边缘蕴含了丰富的内在信息，如方向、阶跃性质、形状等，沿边缘走向的像素变化平缓，而垂直于边缘方向的像素变化剧烈。

---

图像的大部分信息都集中在边缘部分，边缘确定后实际上就实现了不同区域的分割。

---

边缘检测算子

求取边缘往往要借助一些边缘检测算子，这些算子有的是基于一阶导数的算子，有的是二阶微分算子

Roberts算子、Prewitt算子、Sobel算子它们包含x、y两个方向的模板，每种模板只对相应的方向敏感，对该方向上的方向有明显的输出，而对其他方向的变化响应不大。以下是一些常见的一阶微分算子及其特点：

算子名称	特点
简单微分算子	对噪声敏感，对噪声具有一定放大作用
Roberts算子	去噪声作用小，边缘检测能力优于简单微分算子
Prewitt算子	能够有效抑制噪声的影响，同时能够检测边缘点
Sobel算子	得到的边缘较宽，噪声抑制效果更强
Canny算子	检测的边缘位置准确且边缘较窄

1、Roberts算子

2、Prewitt算子

3、Sobel算子

Sobel算子检测到的边缘相比于Roberts算子的检测结果要连续一些，并且对于图像的细节检测能力更好，且Sobel边缘检测器引入了局部平均，对噪声的影响比较小，效果较好。

4、Canny算子

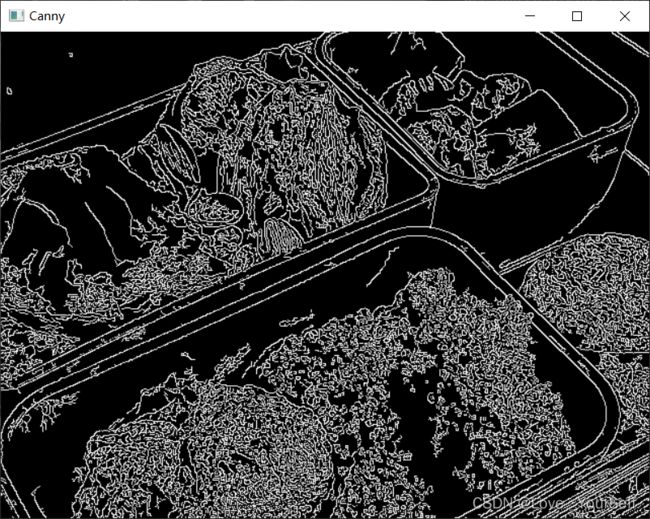
Canny得到的检测结果优于Roberts、Sobel算子的检测结果，边缘细节更丰富，边缘定位准确连续性较好，虚假边缘少且边缘均具有单像素宽度。
其算法实现具体分为以下4步：

1. 用高斯滤波器平滑图像
2. 用一阶偏导的有限差分来计算梯度的幅度和方向
3. 对梯度幅值进行非极大值抑制
4. 用双阈值算法检测和连接边缘

5、拉普拉斯算子

常见的二阶微分算子包括拉普拉斯算子，它是一种二阶导师算子，对图像中的噪声相当敏感，而且检测出的边缘常常是双像素宽，没有方向信息，所以拉普拉斯算子很少直接用于检测边缘，而主要用于已知边缘像素后，确定该像素是在图像的暗区还是明区。另外，一阶差分算子会在较宽范围内形成较大的梯度值，因此不能准确定位，而利用二阶差分算子的过零点可以精确定位边缘。
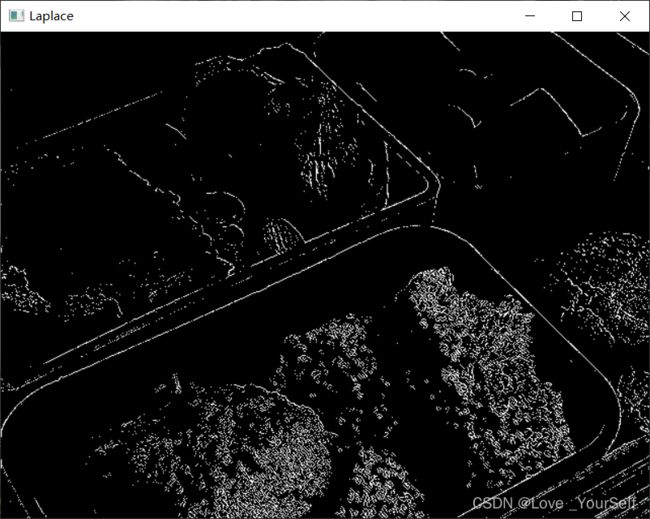
Laplace算子的噪声明显比Sobel算子的噪声大，但其边缘比Sobel要细很多，且Laplace变换作为二阶微分算子对噪声特别敏感，并且会产生双边沿，不能检测边缘方向。

---

效果实验

1、 Roberts边缘检测

Prewitt 算子代码：

Roberts_kernel_x = np.array([[-1, 0], [0, 1]], dtype=int)
Roberts_kernel_y = np.array([[0, -1], [1, 0]], dtype=int)

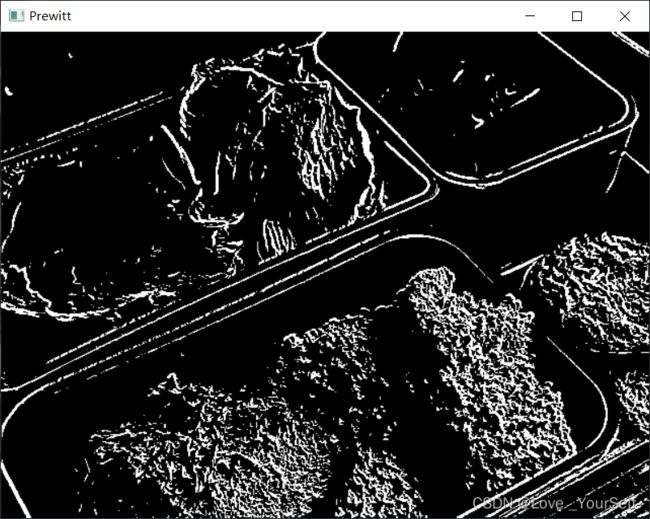
2、Prewitt 边缘检测

Prewitt 算子代码：

Roberts_kernel_x = np.array([[-1, 0], [0, 1]], dtype=int)
Roberts_kernel_y = np.array([[0, -1], [1, 0]], dtype=int)

3、Sobel边缘检测

Sobel函数：

edges = cv2.Sobel(img, -1, 1, 1)

4、Canny边缘检测

Canny函数：

edges = cv2.Canny(img, 5, 100)

5、Laplacian 边缘检测

Laplacian 函数：

edges = cv2.Laplacian(img, -1)

---