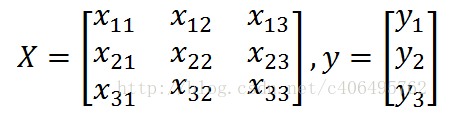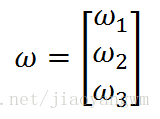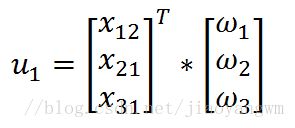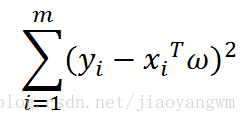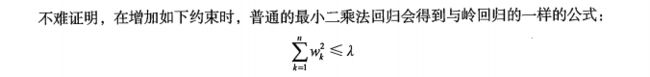【机器学习实战】8、预测数值型数据:回归
文章目录
-
-
- 8.1 用线性回归找到最佳拟合直线
-
- 8.1.1 线性回归
- 8.1.2数据可视化
- 8.1.3 求回归系数向量,并根据系数绘制回归曲线
- 8.2 局部加权线性回归(LWLR)
- 8.3 预测鲍鱼年龄
- 8.4 岭回归
- 8.5 前向逐步回归
- 8.6 预测乐高玩具套件的价格
-
前面章节介绍了分类,分类的目标变量是标称型数据,而本章将会对连续性数据做出预测。
8.1 用线性回归找到最佳拟合直线
回归的目的是预测数值型的目标值。最直接的办法是依据输入写出一个目标值的计算公式。假如你想预测小姐姐男友汽车的功率,可能会这么计算:
H o r s e P o w e r = 0.0015 ∗ a n n u a l S a l a r y − 0.99 ∗ h o u r s L i s t e n i n g T o P u b l i c R a d i o HorsePower = 0.0015 * annualSalary - 0.99 * hoursListeningToPublicRadio HorsePower=0.0015∗annualSalary−0.99∗hoursListeningToPublicRadio
这就是所谓的回归方程(regression equation),其中的0.0015和-0.99称为回归系数(regression weights),求这些回归系数的过程就是回归。一旦有了这些回归系数,再给定输入,做预测就非常容易了。具体的做法是用回归系数乘以输入值,再将结果全部加在一起,就得到了预测值。
说到回归,一般都是指线性回归(linear regression),所以本章里的回归和线性回归代表同一个意思。线性回归意味着可以将输入项分别乘以一些常量,再将结果加起来得到输出。需要说明的是,存在另一种成为非线性回归的回归模型,该模型不认同上面的做法,比如认为输出可能是输入的乘积。这样,上面的功率计算公式也可以写做:
H o r s e P o w e r = 0.0015 ∗ a n n u a l S a l a r y h o u r s L i s t e n i n g T o P u b l i c R a d i o HorsePower = \frac{0.0015 * annualSalary }{ hoursListeningToPublicRadio} HorsePower=hoursListeningToPublicRadio0.0015∗annualSalary
8.1.1 线性回归
如何利用线性回归找到最佳拟合直线?
应该怎么从一大堆数据里求出回归方程呢?假定输入数据存放在矩阵X中,结果存放在向量y中:
而回归系数存放在向量w中:
那么对于给定的数据x1,即矩阵X的第一列数据,预测结果u1将会通过如下公式给出:
现在的问题是,手里有数据矩阵X和对应的标签向量y,怎么才能找到w呢?一个常用的方法就是找出使误差最小的w。这里的误差是指预测u值和真实y值之间的差值,使用该误差的简单累加将使得正差值和负差值相互抵消,所以我们采用平方误差。
平方误差和可以写做:
用矩阵表示还可以写作 ( y − X w ) T ( y − X w ) (y-Xw)^T(y-Xw) (y−Xw)T(y−Xw)
如果对 w w w求导,得到 X T ( Y − X w ) X^T(Y-Xw) XT(Y−Xw),令其等于0,解得 w w w:
w ^ = ( X T X ) − 1 X T y \hat{w}=(X^TX)^{-1}X^Ty w^=(XTX)−1XTy
其中, w ^ \hat{w} w^表示当前可以估计出的 w w w的最优解,即最佳估计。
值得注意的是,上述公式中包含逆矩阵,也就是说,这个方程只在逆矩阵存在的时候使用,也即是这个矩阵是一个方阵,并且其行列式不为0。
述的最佳w求解是统计学中的常见问题,除了矩阵方法外还有很多其他方法可以解决。通过调用NumPy库里的矩阵方法,我们可以仅使用几行代码就完成所需功能。该方法也称作OLS, 意思是“普通小二乘法”(ordinary least squares)。
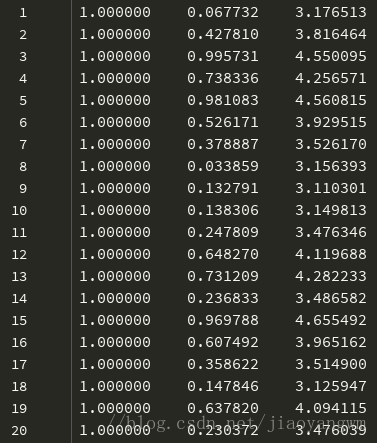
数据集为:ex0.txt
第一列:x0,都为1.0
第二列:x1,x轴的数据
第三列:x2,y轴的数据
8.1.2数据可视化
import numpy as np
import matplotlib.pylab as plt
def loadDataSet(fileName):
"""
加载数据
:param fileName: 文件名
:return:
xArr:x数据集
yArr:y数据集
"""
numFeat=len(open(fileName).readline().split('\t'))-1
xArr=[]
yArr=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=[]
curLine=line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr,yArr
def plotDataSet():
"""
绘制数据集
:return:
"""
xArr,yArr=loadDataSet('ex0.txt')
#数据个数
n=len(xArr)
#样本点
xcord=[]
ycord=[]
for i in range(n):
xcord.append(xArr[i][1])
ycord.append(yArr[i])
fig=plt.figure()
ax=fig.add_subplot(111)
#绘制样本点
ax.scatter(xcord,ycord,s=20,c='blue',alpha=0.5)
plt.title('DataSet')
plt.xlabel('X')
plt.show()
if __name__=='__main__':
plotDataSet()
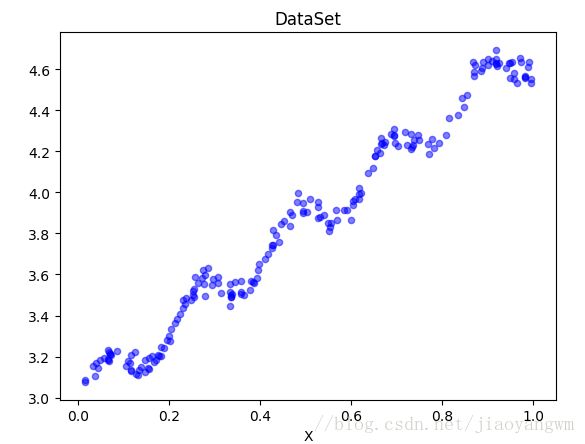
结果:
上图即为数据分布情况
8.1.3 求回归系数向量,并根据系数绘制回归曲线
import numpy as np
import matplotlib.pylab as plt
def loadDataSet(fileName):
"""
加载数据
:param fileName: 文件名
:return:
xArr:x数据集
yArr:y数据集
"""
numFeat=len(open(fileName).readline().split('\t'))-1
xArr=[]
yArr=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=[]
curLine=line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr,yArr
def standRegres(xArr,yArr):
"""
计算回归系数w
:param xArr: x数据集
:param yArr: y数据集
:return: w:回归系数
"""
#np.mat 将序列转化为二维数组
xMat=np.mat(xArr)
yMat=np.mat(yArr).T
xTx=xMat.T*xMat
#np.linalg.inv():矩阵求逆
#np.linalg.det():矩阵求行列式(标量)
#如果行列式为0,则为奇异矩阵,不能求逆
if np.linalg.det(xTx)==0:
print("矩阵为奇异矩阵,不能求逆")
return
#回归系数
# .I为求逆
ws=xTx.I*(xMat.T*yMat)
return ws
def plotRegression():
"""
绘制回归曲线和数据点
:return:
"""
#加载数据集
xArr,yArr=loadDataSet('ex0.txt')
#计算回归系数
ws=standRegres(xArr,yArr)
#创建矩阵
xMat=np.mat(xArr)
yMat=np.mat(yArr)
#深拷贝
xCopy=xMat.copy()
#排序
xCopy.sort(0)
#计算对应的y值
yHat=xCopy*ws
fig=plt.figure()
ax=fig.add_subplot(111)
#绘制回归曲线
ax.plot(xCopy[:,1],yHat,c='red')
#绘制样本点
ax.scatter(xMat[:,1].flatten().A[0],yMat.flatten().A[0],s=20,c='blue',alpha=0.5)
plt.title('DataSet')
plt.xlabel('X')
plt.show()
if __name__=='__main__':
plotRegression()
结果:
如何判断拟合曲线的拟合效果:
根据经验观察,或者使用corrcoef方法,来比较预测值和真实值的相关性,代码如下:
import numpy as np
import matplotlib.pylab as plt
def loadDataSet(fileName):
"""
加载数据
:param fileName: 文件名
:return:
xArr:x数据集
yArr:y数据集
"""
numFeat=len(open(fileName).readline().split('\t'))-1
xArr=[]
yArr=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=[]
curLine=line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr,yArr
def standRegres(xArr,yArr):
"""
计算回归系数w
:param xArr: x数据集
:param yArr: y数据集
:return: w:回归系数
"""
#np.mat 将序列转化为二维数组
xMat=np.mat(xArr)
yMat=np.mat(yArr).T
xTx=xMat.T*xMat
#np.linalg.inv():矩阵求逆
#np.linalg.det():矩阵求行列式(标量)
#如果行列式为0,则为奇异矩阵,不能求逆
if np.linalg.det(xTx)==0:
print("矩阵为奇异矩阵,不能求逆")
return
#回归系数
# .I为求逆
ws=xTx.I*(xMat.T*yMat)
return ws
if __name__=='__main__':
#加载数据集
xArr,yArr=loadDataSet('ex0.txt')
#计算回归系数
ws=standRegres(xArr,yArr)
xMat=np.mat(xArr)
yMat=np.mat(yArr)
yHat=xMat*ws
#np.corrcoef 获得相关系数矩阵
print(np.corrcoef(yHat.T,yMat))
结果:
[[ 1. 0.98647356]
[ 0.98647356 1. ]]
可以看到,对角线上的数据是1.0,因为yMat和自己的匹配是完美的,而YHat和yMat的相关系数为0.98。
最佳拟合直线方法将数据视为直线进行建模,具有十分不错的表现。数据当中似乎还存在其他的潜在模式。那么如何才能利用这些模式呢?我们可以根据数据来局部调整预测,下面就会介绍这种方法。
8.2 局部加权线性回归(LWLR)
线性回归的一个问题是有可能出现欠拟合现象,因为它求的是具有小均方误差的无偏估 计。显而易见,如果模型欠拟合将不能取得好的预测效果。所以有些方法允许在估计中引入一 些偏差,从而降低预测的均方误差。
其中的一个方法是局部加权线性回归(Locally Weighted Linear Regression,LWLR)。在该方法中,我们给待预测点附近的每个点赋予一定的权重。与kNN一样,这种算法每次预测均需要事先选取出对应的数据子集。该算法解除回归系数 W W W的形式如下:
w ^ = ( X T W X ) − 1 X T W y \hat{w}=(X^TWX)^{-1}X^TWy w^=(XTWX)−1XTWy
其中, W W W是一个矩阵,这个公式跟我们上面推导的公式的区别就在于 W W W,它用来给每个点赋予权重。
LWLR使用”核”(与支持向量机中的核类似)来对附近的点赋予更高的权重。核的类型可以自由选择,最常用的核就是高斯核,高斯核对应的权重如下:
w ( i , i ) = e x p ( ∣ x ( i ) − x ∣ − 2 k 2 ) w(i,i)=exp\left (\frac{|x^{(i)}-x|}{-2k^2}\right) w(i,i)=exp(−2k2∣x(i)−x∣)
这样我们就可以根据上述公式,编写局部加权线性回归,我们通过改变k的值,可以调节回归效果,编写代码如下:
# -*- coding:utf-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
"""
函数说明:加载数据
Parameters:
fileName - 文件名
Returns:
xArr - x数据集
yArr - y数据集
Website:
http://www.cuijiahua.com/
Modify:
2017-11-12
"""
numFeat = len(open(fileName).readline().split('\t')) - 1
xArr = []; yArr = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr, yArr
def standRegres(xArr,yArr):
"""
函数说明:计算回归系数w
Parameters:
xArr - x数据集
yArr - y数据集
Returns:
ws - 回归系数
Website:
http://www.cuijiahua.com/
Modify:
2017-11-12
"""
xMat = np.mat(xArr); yMat = np.mat(yArr).T
xTx = xMat.T * xMat #根据文中推导的公示计算回归系数
if np.linalg.det(xTx) == 0.0:
print("矩阵为奇异矩阵,不能求逆")
return
ws = xTx.I * (xMat.T*yMat)
return ws
def plotDataSet():
"""
函数说明:绘制数据集
Parameters:
无
Returns:
无
Website:
http://www.cuijiahua.com/
Modify:
2017-11-12
"""
xArr, yArr = loadDataSet('ex0.txt') #加载数据集
n = len(xArr) #数据个数
xcord = []; ycord = [] #样本点
for i in range(n):
xcord.append(xArr[i][1]); ycord.append(yArr[i]) #样本点
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5) #绘制样本点
plt.title('DataSet') #绘制title
plt.xlabel('X')
plt.show()
def plotRegression():
"""
函数说明:绘制回归曲线和数据点
Parameters:
无
Returns:
无
Website:
http://www.cuijiahua.com/
Modify:
2017-11-12
"""
xArr, yArr = loadDataSet('ex0.txt') #加载数据集
ws = standRegres(xArr, yArr) #计算回归系数
xMat = np.mat(xArr) #创建xMat矩阵
yMat = np.mat(yArr) #创建yMat矩阵
xCopy = xMat.copy() #深拷贝xMat矩阵
xCopy.sort(0) #排序
yHat = xCopy * ws #计算对应的y值
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.plot(xCopy[:, 1], yHat, c = 'red') #绘制回归曲线
ax.scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue',alpha = .5) #绘制样本点
plt.title('DataSet') #绘制title
plt.xlabel('X')
plt.show()
def plotlwlrRegression():
"""
函数说明:绘制多条局部加权回归曲线
Parameters:
无
Returns:
无
Website:
http://www.cuijiahua.com/
Modify:
2017-11-15
"""
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
xArr, yArr = loadDataSet('ex0.txt') #加载数据集
yHat_1 = lwlrTest(xArr, xArr, yArr, 1.0) #根据局部加权线性回归计算yHat
yHat_2 = lwlrTest(xArr, xArr, yArr, 0.01) #根据局部加权线性回归计算yHat
yHat_3 = lwlrTest(xArr, xArr, yArr, 0.003) #根据局部加权线性回归计算yHat
xMat = np.mat(xArr) #创建xMat矩阵
yMat = np.mat(yArr) #创建yMat矩阵
srtInd = xMat[:, 1].argsort(0) #排序,返回索引值
xSort = xMat[srtInd][:,0,:]
fig, axs = plt.subplots(nrows=3, ncols=1,sharex=False, sharey=False, figsize=(10,8))
axs[0].plot(xSort[:, 1], yHat_1[srtInd], c = 'red') #绘制回归曲线
axs[1].plot(xSort[:, 1], yHat_2[srtInd], c = 'red') #绘制回归曲线
axs[2].plot(xSort[:, 1], yHat_3[srtInd], c = 'red') #绘制回归曲线
axs[0].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5) #绘制样本点
axs[1].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5) #绘制样本点
axs[2].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5) #绘制样本点
#设置标题,x轴label,y轴label
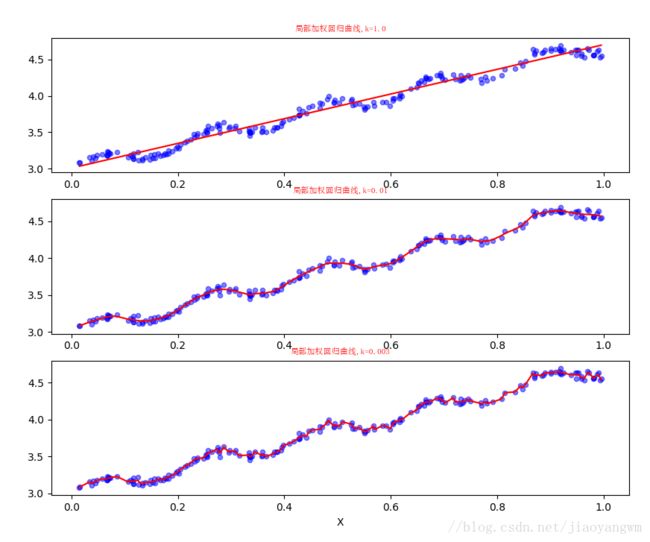
axs0_title_text = axs[0].set_title(u'局部加权回归曲线,k=1.0',FontProperties=font)
axs1_title_text = axs[1].set_title(u'局部加权回归曲线,k=0.01',FontProperties=font)
axs2_title_text = axs[2].set_title(u'局部加权回归曲线,k=0.003',FontProperties=font)
plt.setp(axs0_title_text, size=8, weight='bold', color='red')
plt.setp(axs1_title_text, size=8, weight='bold', color='red')
plt.setp(axs2_title_text, size=8, weight='bold', color='red')
plt.xlabel('X')
plt.show()
def lwlr(testPoint, xArr, yArr, k = 1.0):
"""
函数说明:使用局部加权线性回归计算回归系数w
Parameters:
testPoint - 测试样本点
xArr - x数据集
yArr - y数据集
k - 高斯核的k,自定义参数
Returns:
ws - 回归系数
Website:
http://www.cuijiahua.com/
Modify:
2017-11-15
"""
xMat = np.mat(xArr); yMat = np.mat(yArr).T
m = np.shape(xMat)[0]
weights = np.mat(np.eye((m))) #创建权重对角矩阵
for j in range(m): #遍历数据集计算每个样本的权重
diffMat = testPoint - xMat[j, :]
weights[j, j] = np.exp(diffMat * diffMat.T/(-2.0 * k**2))
xTx = xMat.T * (weights * xMat)
if np.linalg.det(xTx) == 0.0:
print("矩阵为奇异矩阵,不能求逆")
return
ws = xTx.I * (xMat.T * (weights * yMat)) #计算回归系数
return testPoint * ws
def lwlrTest(testArr, xArr, yArr, k=1.0):
"""
函数说明:局部加权线性回归测试
Parameters:
testArr - 测试数据集
xArr - x数据集
yArr - y数据集
k - 高斯核的k,自定义参数
Returns:
ws - 回归系数
Website:
http://www.cuijiahua.com/
Modify:
2017-11-15
"""
m = np.shape(testArr)[0] #计算测试数据集大小
yHat = np.zeros(m)
for i in range(m): #对每个样本点进行预测
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
if __name__ == '__main__':
plotlwlrRegression()
结果:
8.3 预测鲍鱼年龄
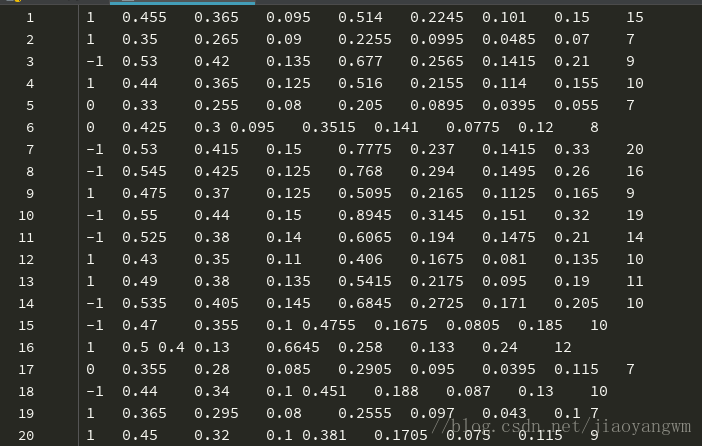
数据集:abalone.txt文件
数据集是多维的,虽然每个数据集的含义并未给出,但是只要知道最后一列数据是y值就可以了。最后一列代表鲍鱼的真实年龄,前几列是鲍鱼的特征。
import matplotlib.pylab as plt
from matplotlib.font_manager import FontProperties
import numpy as np
def loadDataSet(fileName):
"""
加载数据
:param fileName: 文件名
:return:
xArr:x数据集
yArr:y数据集
"""
numFeat = len(open(fileName).readline().split('\t')) - 1
xArr = []; yArr = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr, yArr
def lwlr(testPoint,xArr,yArr,k=1.0):
"""
使用局部加权线性回归计算回归系数w
:param testPoint: 测试样本点
:param xArr: x数据集
:param yArr: y数据集
:param k: 高斯核的k,自定义参数
:return: ws:回归系数
"""
xMat=np.mat(xArr)
yMat=np.mat(yArr).T
m=np.shape(xMat)[0]
# m*m矩阵,创建权重对角阵
weights=np.mat(np.eye((m)))
#遍历数据集计算每个样本的权重
for j in range(m):
diffMat=testPoint-xMat[j,:]
weights[j,j]=np.exp(diffMat*diffMat.T/(-2.0*k**2))
xTx=xMat.T*(weights*xMat)
if np.linalg.det(xTx)==0.0:
print("矩阵为奇异矩阵,不能求逆")
return
ws=xTx.I*(xMat.T*(weights*yMat))
return testPoint*ws
def lwlrTest(testArr,xArr,yArr,k=1.0):
"""
局部加权线性回归测试
:param testArr: 测试数据集,测试集
:param xArr: x数据集,训练集
:param yArr: y数据集,训练集
:param k: 高斯核的k,自定义参数
:return: ws:回归系数
"""
m=np.shape(testArr)[0]
yHat=np.zeros(m)
for i in range(m):
yHat[i]=lwlr(testArr[i],xArr,yArr,k)
return yHat
def standRegres(xArr,yArr):
"""
函数说明:计算回归系数w
Parameters:
xArr - x数据集
yArr - y数据集
Returns:
ws - 回归系数
"""
xMat = np.mat(xArr); yMat = np.mat(yArr).T
xTx = xMat.T * xMat #根据文中推导的公示计算回归系数
if np.linalg.det(xTx) == 0.0:
print("矩阵为奇异矩阵,不能求逆")
return
ws = xTx.I * (xMat.T*yMat)
return ws
def rssError(yArr, yHatArr):
"""
误差大小评价函数
Parameters:
yArr - 真实数据
yHatArr - 预测数据
Returns:
误差大小
"""
return ((yArr - yHatArr) **2).sum()
if __name__ == '__main__':
abX, abY = loadDataSet('abalone.txt')
print('训练集与测试集相同:局部加权线性回归,核k的大小对预测的影响:')
yHat01 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
yHat1 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
yHat10 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
print('k=0.1时,误差大小为:',rssError(abY[0:99], yHat01.T))
print('k=1 时,误差大小为:',rssError(abY[0:99], yHat1.T))
print('k=10 时,误差大小为:',rssError(abY[0:99], yHat10.T))
print('')
print('训练集与测试集不同:局部加权线性回归,核k的大小是越小越好吗?更换数据集,测试结果如下:')
yHat01 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
yHat1 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
print('k=0.1时,误差大小为:',rssError(abY[100:199], yHat01.T))
print('k=1 时,误差大小为:',rssError(abY[100:199], yHat1.T))
print('k=10 时,误差大小为:',rssError(abY[100:199], yHat10.T))
print('')
print('训练集与测试集不同:简单的线性归回与k=1时的局部加权线性回归对比:')
print('k=1时,误差大小为:', rssError(abY[100:199], yHat1.T))
ws = standRegres(abX[0:99], abY[0:99])
yHat = np.mat(abX[100:199]) * ws
print('简单的线性回归误差大小:', rssError(abY[100:199], yHat.T.A))
结果:
k=1 时,误差大小为: 429.89056187
k=10 时,误差大小为: 549.118170883
训练集与测试集不同:局部加权线性回归,核k的大小是越小越好吗?更换数据集,测试结果如下:
k=0.1时,误差大小为: 25119.4591112
k=1 时,误差大小为: 573.52614419
k=10 时,误差大小为: 517.571190538
训练集与测试集不同:简单的线性归回与k=1时的局部加权线性回归对比:
k=1时,误差大小为: 573.52614419
简单的线性回归误差大小: 518.636315325
结论:
- 当k=0.1时,训练集误差很小,但是应用到测试集时,误差反而变大了,这就是过拟合现象。
- 当k=1时,加权回归和简单的线性回归效果差不多
- 表明选取最佳模型必须要在未知数据集上比较才能得到
- 如何确定最佳效果:使用不同的10个样本集做测试来比较
- 局部加权线性回归中,过小的核可能导致过拟合现象,即训练集表现良好,测试集表现很差。
局部加权线性回归能够取得比普通的更好的效果,但其问题在于每次必须在整个数据集上运行,也就是为了做出预测,必须保存所有的训练数据。
8.4 岭回归
如果数据的特征比样本点还多应该怎么办?很显然,此时我们不能再使用上文的方法进行计算了,因为矩阵X不是满秩矩阵,非满秩矩阵在求逆时会出现问题。为了解决这个问题,统计学家引入岭回归(ridge regression)的概念。
岭回归即我们所说的L2正则线性回归,在一般的线性回归最小化均方误差的基础上增加了一个参数w的L2范数的罚项,从而最小化罚项残差平方和:
简单说来,岭回归就是在普通线性回归的基础上引入单位矩阵。回归系数的计算公式变形如下:
式中,矩阵I是一个mxm的单位矩阵,加上一个λI从而使得矩阵非奇异,进而能对矩阵求逆。
岭回归最先用来处理特征数多于样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里通过引入λ来限制了所有w之和,通过引入该惩罚项,能够减少不重要的参数,这个技术在统计学中也可以叫做缩减(shrinkage)。
缩减方法可以去掉不重要的参数,因此能更好地裂解数据。此外,与简单的线性回归相比,缩减法能够取得更好的预测效果。
代码:
为了使用岭回归和缩减技术,首先需要对特征做标准化处理。因为,我们需要使每个维度特征具有相同的重要性。本文使用的标准化处理比较简单,就是将所有特征都减去各自的均值并除以方差。
代码很简单,只需要稍做修改,其中,λ为模型的参数。我们先绘制一个回归系数与log(λ)的曲线图,看下它们的规律,编写代码如下:
# -*-coding:utf-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
"""
函数说明:加载数据
Parameters:
fileName - 文件名
Returns:
xArr - x数据集
yArr - y数据集
"""
numFeat = len(open(fileName).readline().split('\t')) - 1
xArr = []; yArr = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr, yArr
def ridgeRegres(xMat, yMat, lam = 0.2):
"""
函数说明:岭回归
Parameters:
xMat - x数据集
yMat - y数据集
lam - 缩减系数
Returns:
ws - 回归系数
"""
xTx = xMat.T * xMat
denom = xTx + np.eye(np.shape(xMat)[1]) * lam
if np.linalg.det(denom) == 0.0:
print("矩阵为奇异矩阵,不能转置")
return
ws = denom.I * (xMat.T * yMat)
return ws
def ridgeTest(xArr, yArr):
"""
函数说明:岭回归测试
Parameters:
xMat - x数据集
yMat - y数据集
Returns:
wMat - 回归系数矩阵
"""
xMat = np.mat(xArr); yMat = np.mat(yArr).T
#数据标准化
yMean = np.mean(yMat, axis = 0) #行与行操作,求均值
yMat = yMat - yMean #数据减去均值
xMeans = np.mean(xMat, axis = 0) #行与行操作,求均值
xVar = np.var(xMat, axis = 0) #行与行操作,求方差
xMat = (xMat - xMeans) / xVar #数据减去均值除以方差实现标准化
numTestPts = 30 #30个不同的lambda测试
wMat = np.zeros((numTestPts, np.shape(xMat)[1])) #初始回归系数矩阵
for i in range(numTestPts): #改变lambda计算回归系数
ws = ridgeRegres(xMat, yMat, np.exp(i - 10)) #lambda以e的指数变化,最初是一个非常小的数,
wMat[i, :] = ws.T #计算回归系数矩阵
return wMat
def plotwMat():
"""
函数说明:绘制岭回归系数矩阵
"""
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
abX, abY = loadDataSet('abalone.txt')
redgeWeights = ridgeTest(abX, abY)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(redgeWeights)
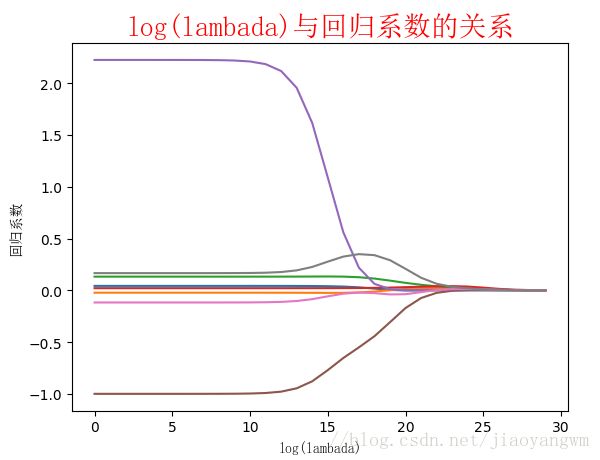
ax_title_text = ax.set_title(u'log(lambada)与回归系数的关系', FontProperties = font)
ax_xlabel_text = ax.set_xlabel(u'log(lambada)', FontProperties = font)
ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties = font)
plt.setp(ax_title_text, size = 20, weight = 'bold', color = 'red')
plt.setp(ax_xlabel_text, size = 10, weight = 'bold', color = 'black')
plt.setp(ax_ylabel_text, size = 10, weight = 'bold', color = 'black')
plt.show()
if __name__ == '__main__':
plotwMat()
结果:
结果分析:
上图绘制了回归系数和 l o g ( λ ) log(\lambda) log(λ)的关系,最左边时即 λ \lambda λ最小时,可以的是所有系数的原始值(与线性回归一致),最右边系数全部缩减为0,中间的某个位置将会得到最好的预测结果。
如何得到最佳参数 λ \lambda λ:使用交叉验证
lasso(普通最小二乘回归)
8.5 前向逐步回归
前向逐步线性回归算法属于一种贪心算法,即每一步都尽可能减少误差。一开始,所有的权重都设置为1,然后每一步所做的决策是对某个权重增加或减少一个很小的值。
我们计算回归系数,不再是通过公式计算,而是通过每次微调各个回归系数,然后计算预测误差。那个使误差最小的一组回归系数,就是我们需要的最佳回归系数。

前向逐步线性回归实现也很简单。当然,还是先进行数据标准化,编写代码如下:
# -*-coding:utf-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
"""
函数说明:加载数据
Parameters:
fileName - 文件名
Returns:
xArr - x数据集
yArr - y数据集
"""
numFeat = len(open(fileName).readline().split('\t')) - 1
xArr = [];
yArr = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
xArr.append(lineArr)
yArr.append(float(curLine[-1]))
return xArr, yArr
def regularize(xMat, yMat):
"""
函数说明:数据标准化
Parameters:
xMat - x数据集
yMat - y数据集
Returns:
inxMat - 标准化后的x数据集
inyMat - 标准化后的y数据集
"""
inxMat = xMat.copy() # 数据拷贝
inyMat = yMat.copy()
yMean = np.mean(yMat, 0) # 行与行操作,求均值
inyMat = yMat - yMean # 数据减去均值
inMeans = np.mean(inxMat, 0) # 行与行操作,求均值
inVar = np.var(inxMat, 0) # 行与行操作,求方差
inxMat = (inxMat - inMeans) / inVar # 数据减去均值除以方差实现标准化
return inxMat, inyMat
def rssError(yArr, yHatArr):
"""
函数说明:计算平方误差
Parameters:
yArr - 预测值
yHatArr - 真实值
Returns:
"""
return ((yArr - yHatArr) ** 2).sum()
def stageWise(xArr, yArr, eps=0.01, numIt=100):
"""
函数说明:前向逐步线性回归
Parameters:
xArr - x输入数据
yArr - y预测数据
eps - 每次迭代需要调整的步长
numIt - 迭代次数
Returns:
returnMat - numIt次迭代的回归系数矩阵
"""
xMat = np.mat(xArr);
yMat = np.mat(yArr).T # 数据集
xMat, yMat = regularize(xMat, yMat) # 数据标准化
m, n = np.shape(xMat)
returnMat = np.zeros((numIt, n)) # 初始化numIt次迭代的回归系数矩阵
ws = np.zeros((n, 1)) # 初始化回归系数矩阵
wsTest = ws.copy()
wsMax = ws.copy()
for i in range(numIt): # 迭代numIt次
# print(ws.T) #打印当前回归系数矩阵
lowestError = float('inf') # 正无穷
for j in range(n): # 遍历每个特征的回归系数
for sign in [-1, 1]:
wsTest = ws.copy()
wsTest[j] += eps * sign # 微调回归系数
yTest = xMat * wsTest # 计算预测值
rssE = rssError(yMat.A, yTest.A) # 计算平方误差
if rssE < lowestError: # 如果误差更小,则更新当前的最佳回归系数
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i, :] = ws.T # 记录numIt次迭代的回归系数矩阵
return returnMat
def plotstageWiseMat():
"""
函数说明:绘制岭回归系数矩阵
"""
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
xArr, yArr = loadDataSet('abalone.txt')
returnMat = stageWise(xArr, yArr, 0.005, 1000)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(returnMat)
ax_title_text = ax.set_title(u'前向逐步回归:迭代次数与回归系数的关系', FontProperties=font)
ax_xlabel_text = ax.set_xlabel(u'迭代次数', FontProperties=font)
ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties=font)
plt.setp(ax_title_text, size=15, weight='bold', color='red')
plt.setp(ax_xlabel_text, size=10, weight='bold', color='black')
plt.setp(ax_ylabel_text, size=10, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
plotstageWiseMat()
结果:
缩减方法(逐步线性回归或岭回归),就是将一些系数缩减成很小的值或者直接缩减为0。这样做,就增大了模型的偏差(减少了一些特征的权重),通过把一些特征的回归系数缩减到0,同时也就减少了模型的复杂度。消除了多余的特征之后,模型更容易理解,同时也降低了预测误差。但是当缩减过于严厉的时候,就会出现过拟合的现象,即用训练集预测结果很好,用测试集预测就糟糕很多。
8.6 预测乐高玩具套件的价格
使用sklearn的linear_model
官网链接
class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=’auto’, random_state=None)
参数说明如下:
- alpha:正则化系数,float类型,默认为1.0。正则化改善了问题的条件并减少了估计的方差。较大的值指定较强的正则化。
- fit_intercept:是否需要截距,bool类型,默认为True。也就是是否求解b。
- normalize:是否先进行归一化,bool类型,默认为False。如果为真,则回归X将在回归之前被归一化。 当fit_intercept设置为False时,将忽略此参数。 当回归量归一化时,注意到这使得超参数学习更加鲁棒,并且几乎不依赖于样本的数量。 相同的属性对标准化数据无效。然而,如果你想标准化,请在调用normalize = False训练估计器之前,使用preprocessing.StandardScaler处理数据。
- copy_X:是否复制X数组,bool类型,默认为True,如果为True,将复制X数组; 否则,它覆盖原数组X。
- max_iter:最大的迭代次数,int类型,默认为None,最大的迭代次数,对于sparse_cg和lsqr而言,默认次数取决于scipy.sparse.linalg,对于sag而言,则默认为1000次。
- tol:精度,float类型,默认为0.001。就是解的精度。
- solver:求解方法,str类型,默认为auto。可选参数为:auto、svd、cholesky、lsqr、sparse_cg、sag。
- auto根据数据类型自动选择求解器。
- svd使用X的奇异值分解来计算Ridge系数。对于奇异矩阵比cholesky更稳定。
- cholesky使用标准的scipy.linalg.solve函数来获得闭合形式的解。
- sparse_cg使用在scipy.sparse.linalg.cg中找到的共轭梯度求解器。作为迭代算法,这个求解器比大规模数据(设置tol和max_iter的可能性)的cholesky更合适。
- lsqr使用专用的正则化最小二乘常数scipy.sparse.linalg.lsqr。它是最快的,但可能在旧的scipy版本不可用。它是使用迭代过程。
- sag使用随机平均梯度下降。它也使用迭代过程,并且当n_samples和n_feature都很大时,通常比其他求解器更快。注意,sag快速收敛仅在具有近似相同尺度的特征上被保证。您可以使用sklearn.preprocessing的缩放器预处理数据。
- random_state:sag的伪随机种子。
以上就是所有的初始化参数,当然,初始化后还可以通过set_params方法重新进行设定。
import numpy as np
from bs4 import BeautifulSoup
import random
def scrapePage(retX,retY,inFile,yr,numPce,origPrc):
"""
从页面读取数据,生成retX,retY列表
:param retX: 数据X
:param retY: 数据Y
:param inFile: HTML文件
:param yr: 年份
:param numPce:乐高部件数目
:param origPrc: 原价
:return: 无
"""
with open(inFile,encoding='utf-8') as f:
html=f.read()
soup=BeautifulSoup(html)
i=1
#根据HTML页面结构进行解析
currentRow=soup.find_all('table',r="%d" % i)
while(len(currentRow) !=0 ):
currentRow = soup.find_all('table', r="%d" % i)
title = currentRow[0].find_all('a')[1].text
lwrTitle = title.lower()
# 查找是否有全新标签
if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
newFlag = 1.0
else:
newFlag = 0.0
# 查找是否已经标志出售,我们只收集已出售的数据
soldUnicde = currentRow[0].find_all('td')[3].find_all('span')
if len(soldUnicde) == 0:
print("商品 #%d 没有出售" % i)
else:
# 解析页面获取当前价格
soldPrice = currentRow[0].find_all('td')[4]
priceStr = soldPrice.text
priceStr = priceStr.replace('$', '')
priceStr = priceStr.replace(',', '')
if len(soldPrice) > 1:
priceStr = priceStr.replace('Free shipping', '')
sellingPrice = float(priceStr)
# 去掉不完整的套装价格
if sellingPrice > origPrc * 0.5:
print("%d\t%d\t%d\t%f\t%f" % (yr, numPce, newFlag, origPrc, sellingPrice))
retX.append([yr, numPce, newFlag, origPrc])
retY.append(sellingPrice)
i += 1
currentRow = soup.find_all('table', r="%d" % i)
def setDataCollect(retX, retY):
"""
函数说明:依次读取六种乐高套装的数据,并生成数据矩阵
Parameters:
无
Returns:
无
"""
scrapePage(retX, retY, './lego/lego8288.html', 2006, 800, 49.99) # 2006年的乐高8288,部件数目800,原价49.99
scrapePage(retX, retY, './lego/lego10030.html', 2002, 3096, 269.99) # 2002年的乐高10030,部件数目3096,原价269.99
scrapePage(retX, retY, './lego/lego10179.html', 2007, 5195, 499.99) # 2007年的乐高10179,部件数目5195,原价499.99
scrapePage(retX, retY, './lego/lego10181.html', 2007, 3428, 199.99) # 2007年的乐高10181,部件数目3428,原价199.99
scrapePage(retX, retY, './lego/lego10189.html', 2008, 5922, 299.99) # 2008年的乐高10189,部件数目5922,原价299.99
scrapePage(retX, retY, './lego/lego10196.html', 2009, 3263, 249.99) # 2009年的乐高10196,部件数目3263,原价249.99
def usesklearn():
"""
函数说明:使用sklearn
Parameters:
无
Returns:
"""
from sklearn import linear_model
reg = linear_model.Ridge(alpha=.5)
lgX = []
lgY = []
setDataCollect(lgX, lgY)
reg.fit(lgX, lgY)
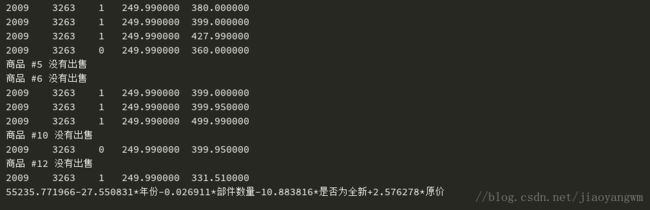
print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % (
reg.intercept_, reg.coef_[0], reg.coef_[1], reg.coef_[2], reg.coef_[3]))
if __name__ == '__main__':
usesklearn()
结果:
总结:
与分类一样,回归也是预测目标值的过程。回归与分类的不同点在于,前者预测连续类型变量,而后者预测离散类型变量。
岭回归是缩减法的一种,相当于对回归系数的大小施加了限制。另一种很好的缩减法是lasso。lasso难以求解,但可以使用计算简便的逐步线性回归方法求的近似解。
缩减法还可以看做是对一个模型增加偏差的同时减少方法。