【吴恩达机器学习 - 3】利用fmincg函数与正则化实现多元分类问题及神经网络初体验(课后练习第三题ex3)
目录
-
- 1. 多元分类
-
- 1.1 代价函数
- 1.2 求最优参数
- 1.3 分类预测
- 2. 神经网络
照旧,本练习的相关资料链接将会扔到评论区,大家自取
1. 多元分类
在上一节练习中已经完成了逻辑回归,也就是分类问题,实际上只是完成了二分类问题,而本节练习将会使用逻辑回归完成手写字体识别(多元分类)问题
1.1 代价函数
该节练习的第一个内容就是完成多分类问题的代价函数,实际上,多分类问题的本质仍然是逻辑回归,因此该代价函数与上节练习所用到的代价函数一致,不过在该节中我换了一种与上节练习不同的写法,有兴趣的同学可以对比一下异同,把它写进lrCostFunction.m文件即可
h = sigmoid(X*theta);
theta(1) = 0;
J = -sum(y.*log(h)+(1-y).*log(1-h))/m + lambda*sum(theta.^2)/2/m;
grad = sum((h-y).*X)/m + lambda*theta'/m;
1.2 求最优参数
代价函数就写好了,那怎么进行梯度下降呢?在上一节练习中我们是利用fminunc函数进行最优化参数的求解,而在这一节当中将使用fmincg函数进行求解(至于为什么这个,我也不是很清楚,作业提示用这个就对了,但我查过相关资料说fmincg比fminunc效率更高)
在oneVsAll.m文件中,明确提醒你使用fmincg函数

这时候你可能会有疑问,二分类我就会,多分类怎么搞?一个最简单直接的方法,我训练多个分类器不就完了?对的,这里确实就是这么干的,并且他也明确地提示你要使用for-loop的ok?

这就通俗易懂了,啪啪啪,往oneVsAll.m文件中敲下如下代码
for c = 1:num_labels
initial_theta = zeros(n + 1, 1);
options = optimset('GradObj', 'on', 'MaxIter', 50);
[theta] = ...
fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
initial_theta, options);
all_theta(c,:) = theta;
endfor

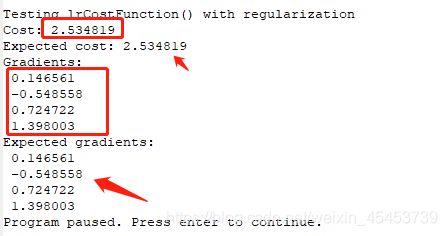
这里作业并没有给出参考值,但你可以通过提交你的代码来进行检测,若没有注册课程账户,你也可以对比你的值跟我的是否大概一样(我的已经通过代码检测了)
1.3 分类预测
接下来的这个就是重头戏了,怎么知道这种多个分类器的想法是否可行呢?实打实地来检验一下就知道了
你只需要在predictoneVsAll.m文件中敲下这行代码
[row p] = max(X * all_theta',[],2);

继续运行一下便可以得到我们训练的准确率是达到了95%

这与作业指导书上是一致的

换言之,以后遇到该种多分类问题,你都可以通过训练多个分类器来实现
2. 神经网络
上述的问题只是十个类型的分类,万一有100个,1000个呢?这时候使用如此简单粗暴的方法就显得有点力不从心了,这时候就是神经网络的表演时刻了
如图是该作业神经网络的模型图,而神经元之间的权值已经提前训练好了,我们只需要知道怎么使用就行了
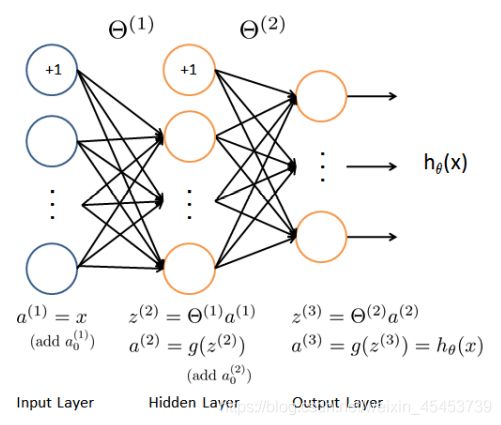
详细的计算思路我也不再描述,对神经网络暂时还不是很理解的同学也可以先把吴恩达老师后面的与神经网络有关的课程看完再过来做这一道题目,这里直接给出代码,往predict.m文件怼上去就是了
a1 = [ones(size(X),1) X];
z2 = a1 * Theta1';
a2 = sigmoid(z2);
a2 = [ones(size(a2),1) a2];
z3 = a2 * Theta2';
[max p] = max(z3,[],2);

这下子我们可以直接来运行ex3_nn.m文件来看看效果了,这时候的正确率相比于使用多个分类器的方法约提高了2.5%
![]()
有兴趣又很无聊的同学也可以继续按下回车,将会为你呈现对应的图片与输出
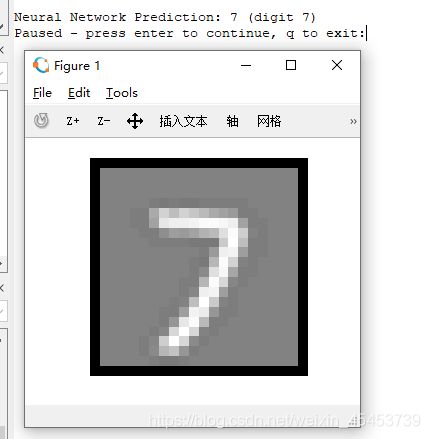
至此,多元分类问题已经可以有一个很有效的解决方法了,至于神经网络的详细训练和使用将在下一节练习与大家分享