【计算机视觉】- 卷积神经网络基础概念

1. 卷积神经网络基础

卷积、池化、ReLU、批归一化、丢弃法(Dropout)

在 手写数字识别 项目中，是运用全连接层提取特征的，也就是将一张图片上的所有像素点展开形成 一维向量 输入网络，但是会存在两个问题

• 输入数据的空间信息被丢失
• 模型的参数过多，容易发生过拟合

为了避免上述问题，引入了卷积神经网络提取特征，既能提取到相邻像素点之间的特征模式，又能保证参数的个数不随图片尺寸变化

说明：在卷积神经网络中，计算范围是在像素点的空间邻域内进行的，卷积核参数的数目也远小于全连接层。卷积核本身与输入图片大小无关，它代表了对空间邻域内某种特征模式的提取。比如，有些卷积核提取物体边缘特征，有些卷积核提取物体拐角处的特征，图像上不同区域共享同一个卷积核。当输入图片大小不一样时，仍然可以共用一个卷积核。

1.1 卷积

卷积核

卷积核的设计比较依靠经验，因此可以在毕业设计中详细阐述过程

在实际项目中，如何设置卷积核，是一个比较重要的问题。但是卷积神经网络的原作者已经将其设计好，一般情况下可以直接使用。

卷积核（kernel）也被叫做滤波器，假设卷积核的高和宽分别为 Kh 和 Kw，则将称为 kh × kw卷积，比如 3×5 卷积，就是指卷积核的高为3, 宽为5。

卷积计算过程

偏置项

在卷积神经网络中，一个卷积算子除了上面描述的卷积过程之外，还包括加上偏置项的操作。例如假设偏置为1，则上面卷积计算的结果为：

0×1+1×2+2×4+3×5 +1=26
0×2+1×3+2×5+3×6 +1=32
0×4+1×5+2×7+3×8 +1=44
0×5+1×6+2×8+3×9 +1=50

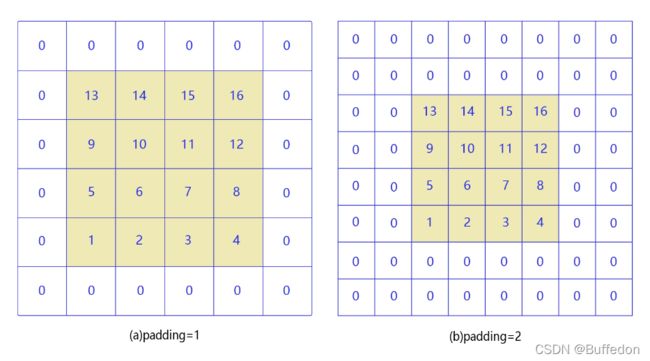
填充(padding)

为什么要进行图片填充？

• 这样输出之后，图片还是原来的大小。一般采取等量填充

示例：

步幅

在卷积计算过程中，卷积核每次滑动的像素点的个数

多输入通道

在实际应用中，问题比较复杂。对于彩色图片，有RGB 三个通道，需要处理多输入通道的场景。

通常用 Cin 表示，那么输入的数据形状为 Cin * Hin * Win

多个卷积核分别计算，最后多个通道的卷积核计算值相加

多通道输出

通常用 Cout 表示，这时还需要设计Cout个维度为Cin * Kh * Kw 的卷积核

输出特征图往往也会具有多个通道，而且在神经网络的计算过程中常常是把一个批次的样本放在一起计算，因此，需要多通道输入和多通道输出的功能。

示例类似于上述 多通道输入

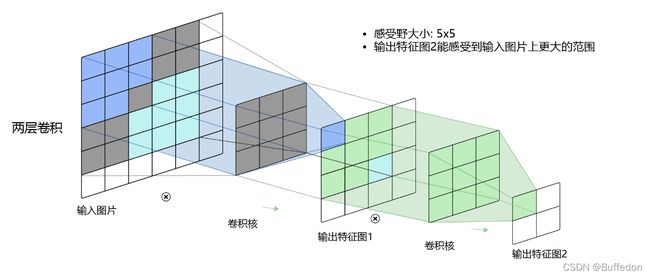
感受野

输出的特征图上的每个像素点 对应 图片中输入数据的范围（某个卷积核计算的范围）

多层卷积的情况：

因此，当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像信息

1.2 池化

能够降低位置对特征的敏感度，并且池化后的特征图会变小，后面连接全连接层，能有效减小神经元的个数，节省存储空间并提高计算效率

池化：使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出

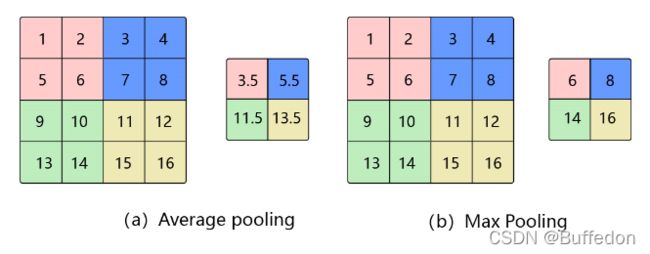
分类：平均池化、最大池化

下面使用了 2*2 的窗口，步幅为2

池化的意义：

• 当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变，池化能够帮助输入的表示近似不变
• 由于池化之后特征图会变小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率

池化的特点：

• 没有学习参数
• 通道数不变，每个通道独立的进行池化
• 对微小的位置变化具有鲁棒性

池化参数

池化窗口的大小、池化窗口滑动步幅、图片填充

比较常见的参数配置：

Kh = Kw = 2
stride_h = stride_w = 2
ph = pw = 2

1.3 激活函数

为什么要有激活函数

卷积和池化都是线性的，但是目标分类(或目标检测)问题都是非线性的，因此通常在卷积或者全连接这样的操作之后，会加上一个非线性的函数，作用在每一个神经元的输出上，从而实现非线性变换的效果

最初的卷积神经网络模型选用的是 sigmoid函数，但是在逐步反向传播的过程中，会出现梯度消失的情况，因此并不合适

经过发展，后面就选用了 ReLU 激活函数，因为在x>0的地方，ReLU函数的导数为1，能够将y的梯度完整的传递给x，而不会引起梯度消失的情况

梯度消失：

在神经网络里，竞经过反向传播之后，梯度值衰减到接近于零的现象称作梯度消失现象

1.4 批归一化 Batch Normalization

批归一化方法：其目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定

在模型学习的过程中，输入有可能是扫描图片，有可能是卫星图片，还有可能是相机图片，这些图片都作为输入的话，分布式不稳定的。此外，由于参数是不断更新的，即使输入数据已经做过标准化处理，但是对于比较靠后的那些层，其接收到的输入是剧烈变化的，通常会导致数值不稳定，模型很难收敛

通常我们会对中间层的输出做标准化处理，处理后的样本数据集满足均值为0，方差为1的统计分布，这是因为当输入数据的分布比较稳定时，有利于算法的稳定和收敛

批归一化好处：

• 可以使学习快速进行
• 可以降低模型对初始值的敏感性
• 可以从一定程度上抑制过拟合

注意：

区分训练过程 和 预测过程的 BatchNorm 的计算

保存训练时计算的均值和方差，在预测时不需要重新计算，直接将训练时计算好的数据加载进来即可

计算归一化输出值：

1. 计算样本中 输入值的均值和方差（注意计算的是每一行 还是每一列）
2. 利用公式 （数组元素值 - 均值）/ 标准差 计算出归一化后的数据

# 输入数据形状是 [N, K]时的示例
import numpy as np
import paddle
from paddle.nn import BatchNorm1D

# 创建数据
data = np.array([[1,2,3], [4,5,6], [7,8,9]]).astype('float32')
# 使用BatchNorm1D计算归一化的输出
# 输入数据维度[N, K]，num_features等于K
bn = BatchNorm1D(num_features=3)    
print(bn)
print('-----------------------------------------------------')
x = paddle.to_tensor(data)
print(x)
print('-----------------------------------------------------')
y = bn(x)
print('output of BatchNorm1D Layer: \n {}'.format(y.numpy()))
print('-----------------------------------------------------')


# 使用Numpy计算均值、方差和归一化的输出
# 这里对第0个特征进行验证
a = np.array([1,4,7])
a_mean = a.mean()
print(a_mean)
print('-----------------------------------------------------')
a_std = np.std(a,axis=0)
print(a_std)
print('-----------------------------------------------------')
b = (a - a_mean) / a_std
print('std {}, mean {}, \n output {}'.format(a_mean, a_std, b))
print('-----------------------------------------------------')

1.5 丢弃法 Dropout

作用：一种抑制过拟合的方法。

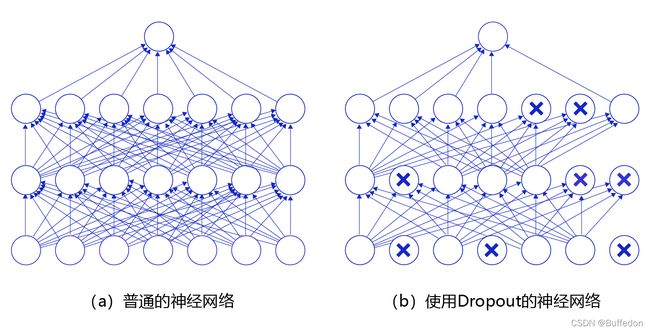
做法：在神经网络学习的过程中，随机删除一部分神经元。训练时，随机选择一部分神经元，将其设置为0，这些神经元将不对外传递信号

如图所示：

在预测场景时，会向前传递所有神经元的信号，可能会引出一个新的问题：训练时由于部分神经元被随机丢弃了，输出数据的总大小会变小。

为了解决这个问题，飞桨支持如下两种方法：

• downscale_in_infer

1. 训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号；

2. 预测时向后传递所有神经元的信号，但是将每个神经元上的数值乘以 (1−r)。

• upscale_in_train

1. 训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号，但是将那些被保留的神经元上的数值除以 (1−r)；

2. 预测时向后传递所有神经元的信号，不做任何处理

2. 参考

更多案例参考：https://aistudio.baidu.com/aistudio/projectdetail/3785901