李宏毅机器学习-卷积神经网络

写在前面

以算法区分深度学习应用，算法类别可分成三大类：

• 常用于影像数据进行分析处理的卷积神经网络(简称CNN)
• 文本分析或自然语言处理的递归神经网络(简称RNN)
• 常用于数据生成或非监督式学习应用的生成对抗网络(简称GAN)

为什么用CNN

一般来说，当我们直接用fully connected feedforward network来做影像处理的时候，往往会需要太多的参数。而CNN做的事就是简化neural network的架构。

Property1：Small Region

• 为什么可以把一些参数拿掉？（为什么可以用比较少的参数可以来做影像处理这件事？）
  • 对一个neural来说，假设要知道一个image里有没有某一个pattern出现，其实不需要看整张image，而只要看image的一小部分。

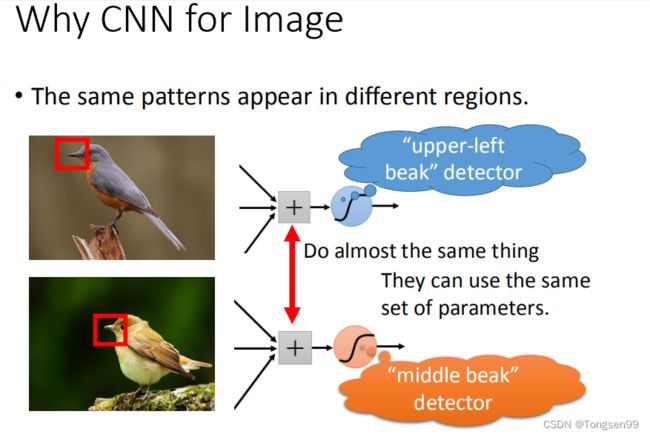
Property2：Same Patterns

• 同样的pattern在image里面，可能会出现在image不同的部分，但是代表的是同样的含义，它们有同样的形状，可以用同样的neural，同样的参数，就可以把pattern侦测出来。

比如，两张鸟嘴在两张图片的不同位置，nerual侦测左上角的鸟嘴和侦测中央的鸟嘴做的事情是一样的。我们并不需要两个neural去做两组参数，我们要求这两个neural用同一组参数，就样就可以减少需要参数的量。

Property3：Subsampling

我们知道一个image可以做subsampling，把一个image的奇数行，偶数列的pixel（像素）拿掉，变成原来十分之一的大小，这其实不会影响人对这张image的理解。对你来说：这两张image看起来可能没有太大的差别，是没有太大的影响的。所以我们就可以用这样的概念把image变小，这样就可以减少需要的参数。

CNN架构

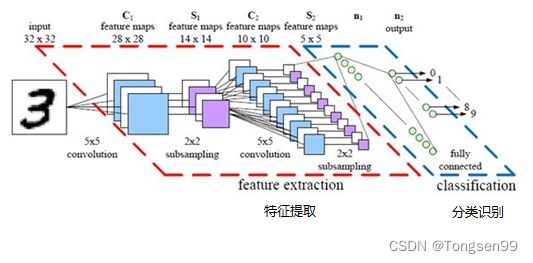
结构简介

• 卷积层（Convolutional layer）：卷积神经网络中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征。第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。
• 线性整流层（Rectified Linear Units layer, ReLU layer）：这一层神经的活性化函数（Activation function）使用线性整流（Rectified Linear Units, ReLU）。
• 池化层（Pooling layer）：通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取其最大值或平均值，得到新的、维度较小的特征。
• 全连接层（ Fully-Connected layer）：把所有局部特征结合变成全局特征，用来计算最后每一类的得分。

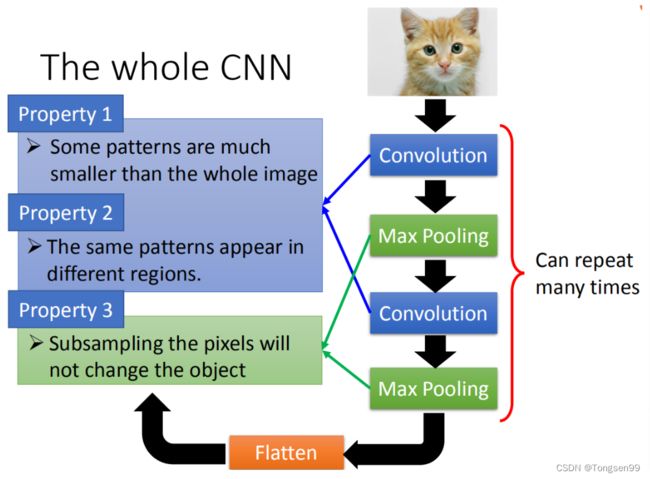
• Step1：input一张image
• Step2：通过Convolution Layer（output进行ReLU）⇒ Max Pooling ⇒ 通过Convolution Layer（output进行ReLU）⇒ Max Pooling ⇒ 循环前两个步骤……直到次数足够多（反复多少次是要事先决定的，它就是network的架构(就像neural有几层一样)。要做几层的Convolution，做几层的Max Pooling，在定neural架构的时候要事先决定好）
• Step3：Flatten
• Step4：Fully Connected Feedforward network ⇒ 得到影像辨识的结果

• 对于Small Region，Same Patterns，Subsampling，前面两个可以用Convolution来处理，最后一个可以用Max Pooling来处理。

Convolution

一些卷积层的基本概念

• 输入特征图
  卷积层的输入数据
• 输出特征图
  卷积层输出数据
• 感受野
  每个隐含单元连接的输入区域大小叫神经元的感受野(receptive field)，感受野一般为过滤器的大小。
• 过滤器
  卷积层的参数包含一系列过滤器（filter），每个过滤器训练一个深度。有几个过滤器输出单元就具有多少深度。

Property1

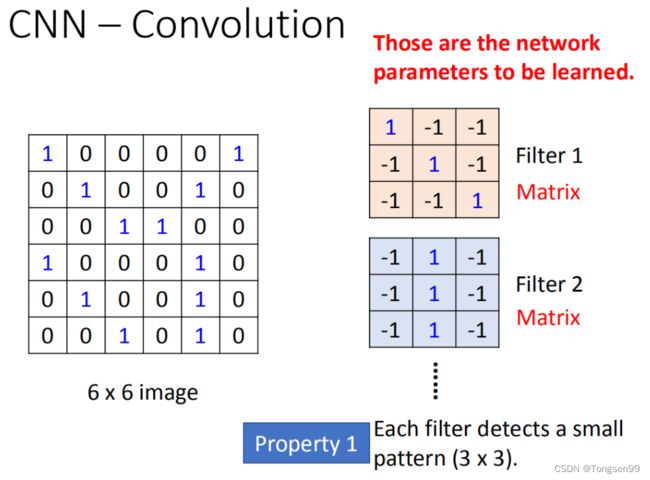
假设现在我们的network的input是一张$6\ast 6$的image，如果是黑白的，一个pixel就只需要用一个value去描述它。在convolution layer里面，它由一组filter，(其中每一个filter其实就等同于是fully connected layer里面的一个neuron)，每一个filter在这里就是一个matrix($3\ast 3$)，这每个filter里面的参数(matrix里面每一个element值)就是network的parameter(这些parameter是要学习出来的，并不是需要人去设计的)。

• 每个filter如果是$3\ast 3$的detects，意味着它是在侦测一个$3\ast 3$的pattern(看$3\ast 3$的一个范围)。在侦测pattern的时候不看整张image，只看一个$3\ast 3$范围就可以决定有没有某一个pattern的出现。这个就是我们考虑的第一个Property。

Property2

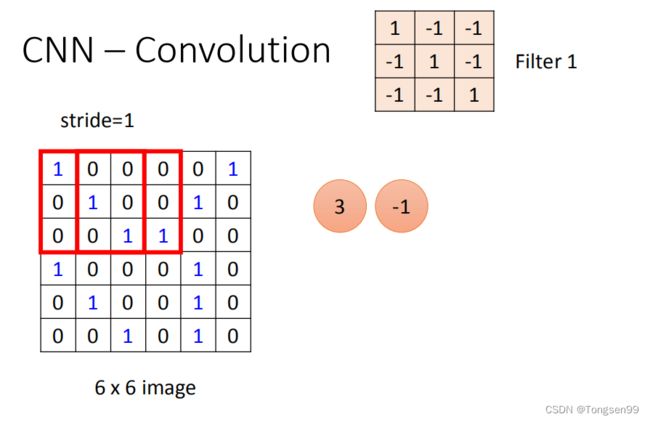
第一个filter是一个$3\ast 3$的matrix，把这个filter放在image的左上角，把filter的9个值和image的9个值做内积，内积的结果就得到3。然后向右移动。

• 移动多少是事先决定的，移动的距离叫做stride(stride等于多少，自己设计)。
• 如果步幅很小（比如 stride = 1），相邻隐含单元的输入区域的重叠部分会很多；步幅很大则重叠区域变少。

把filter往右移动到右边界，接下来往下移动一格，再从左到右继续移动，以此类推，直到把filter移到右下角的时候，得到的值如上图所示。
上图中的蓝色直线代表了左上和左下出现所得到结果中的最大的值，说明这个filter要侦测的pattern出现在这张image的左上角和左下角，这件事情就考虑了property2。即同一个pattern出现在了左上角的位置和左下角的位置，我们就可以用Filter1侦测出来，并不需要不同的filter来做这件事。

在一个convolution layer里面会有很多的filter，另外的filter会有不同的参数(如图中显示的Filter2)，它也做跟Filter1一模一样的事情，从而得到了另一个$4\ast 4$的matrix。

• 红色的matrix和蓝色的matrix合起来就叫做feature map。

若换成彩色的image，而彩色的image是由RGB组成的，所以一个彩色的image就是好几个matrix叠在一起，就是一个立方体。如果要处理彩色image，这时候filter不是一个matrix，而是一个立方体。如果用RGB表示一个pixel的话，那么input就是$3\ast 6\ast 6$，filter就是$3\ast 3\ast 3$。
在做convolution时将filter的值和image的值做内积(不是把每一个channel分开来算，而是合在一起来算，一个filter就考虑了不同颜色所代表的channel)。即通道方向上有多个特征图时，会按照通道输入数据和过滤器的卷积运算，并将结果相加。如下图所示。

convolution和fully connected之间的关系

• convolution就是fully connected layer把一些weight拿掉了。经过convolution的output其实就是一个hidden layer的neural的output。

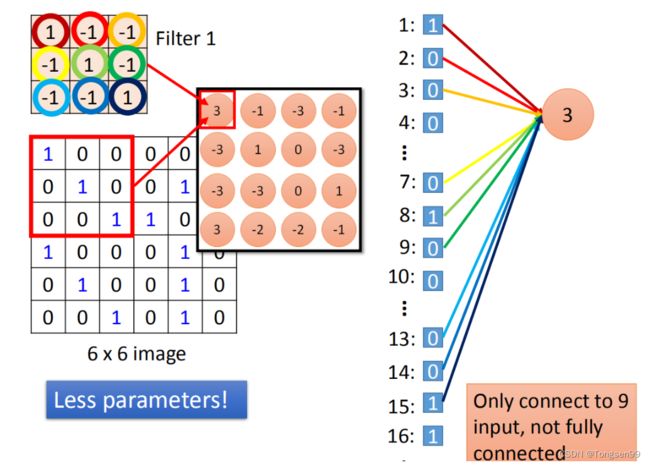
在fully connected中，一个neural应该连接所有的input(这里有36个pixel当做input，则这个neuron应连接在36个input上)，但是现在只连接了9个input(侦测一个pattern，不需要看整张image，看9个input就行)，这样做就用了比较少的参数。

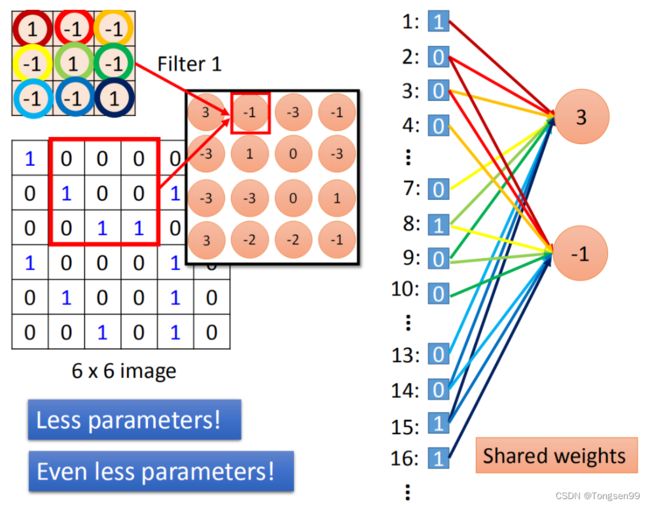
两个neural本来在fully connected里面有自己的weight，但当我们在做convolution时，把每一个neural连接的weight减少，强迫这两个neural共用一个weight，这件事叫做shared weight。当我们做这件事的时候，我们用的参数就比原来的更少。
比如说，我们把同一深度的平面叫做深度切片(depth slice)（e.g. a volume of size [55x55x96] has 96 depth slices, each of size [55x55]），那么同一个切片应该共享同一组权重和偏置。

• 为什么要权重共享呢？
  • 一方面，重复单元能够对特征进行识别，而不考虑它在可视域中的位置。
  • 另一方面，权重共享使得我们能更有效地进行特征抽取，因为它极大的减少了需要学习的自由变量的个数。通过控制模型的规模，卷积网络对视觉问题可以具有很好的泛化能力。

激活函数RelU

• 激活函数的作用是用来加入非线性因素，把卷积层输出结果做非线性映射。
• 常用的激活函数有sigmoid、tanh、relu等等，前两者sigmoid/tanh比较常见于全连接层，后者ReLU常见于卷积层。
• ReLU(The Rectified Linear Unit，修正线性单元)的特点是收敛快，求梯度简单。计算公式也很简单，即max(0,T)，即对于输入的负值，输出全为0；对于正值，则原样输出。

Max Pooling

池化层的基本概念

• 为了有效地减少计算量，CNN使用的另一个有效的工具被称为“池化(Pooling)”。池化就是将输入图像进行缩小，减少像素信息，只保留重要信息。
• 池化（pooling）即下采样（downsamples），目的是为了减少特征图。

池化操作对每个深度切片独立，规模一般为$2＊2$，相对于卷积层进行的卷积运算，池化层进行的运算一般有以下几种：

• 最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。
• 均值池化（Mean Pooling）。取4个点的均值。
• 高斯池化。借鉴高斯模糊的方法。不常用。
• 可训练池化。训练函数ff，接受4个点为输入，出入1个点。不常用。

Max Pooling的步骤

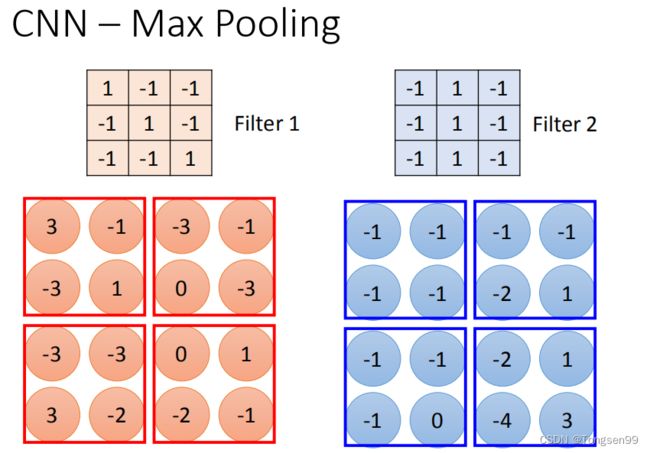
我们根据Filter1得到$4\ast 4$的maxtrix，根据Filter2得到另一个$4\ast 4$的matrix，接下来把output4个一组，每一组里面选择它们的最大。
这就是把四个value合成一个value。这样可以让image缩小。

做完一次convolution和一次max pooling，就将原来$6\ast 6$的image变成了一个$2\ast 2$的image。这个$2\ast 2$的pixel的深度取决于有几个filter。得到结果就是一个new image but smaller，一个filter就代表了一个channel。

这边有一个问题：第一次有25个filter，得到25个feature map，第二次也是有25个filter，那将其做完是不是要得到$25^2$的feature map。其实不是这样的！
假设第一层filter有2个，第二层的filter在考虑这个input时是会考虑深度的，并不是每个channel分开考虑，而是一次考虑所有的channel。所以convolution有多少个filter，output就有多少个filter(convolution有25个filter，output就有25个filter。只不过，这25个filter都是一个立方体)。

Flatten

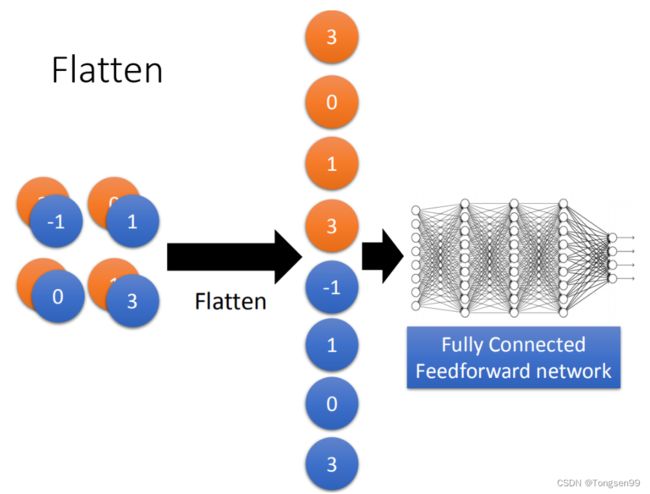
• flatten就是将feature map拉直，拉直之后就可以丢到fully connected feedforward network，然后就结束了。

Fully Connected Feedforward network

• 全连接层在整个卷积神经网络中起到“分类器”的作用，对结果进行识别分类。

演示

CNN in Keras

唯一要改的是：network structure和input format。本来在DNN中input是一个vector，现在CNN会考虑input image的几何空间，所以不能给它一个vector。应该input一个tensor(高维的vector)。（为什么要给三维的vector？因为image的长宽高各是一维，若是彩色的话就是第三维。所以要给三维的tensor。）

CNN学到了什么?

……

Deep Dream

Deep Dream是说：如果你给machine一张image，它会在这张image里加上它看到的东西。咋样做这件事情呢？你先找一张image，然后将这张image丢到CNN中，把它的某一个hidden layer拿出来(vector)，它是一个vector(假设这里是：[3.9, -1.5, 2.3…])。接下来把postitive dimension值调大，把negative dimension值调小(正的变的更正，负的变得更负)。把这个(调节之后的vector)当做是新的image的目标(把3.9的值变大，把-1.5的值变得更负，2.3的值变得更大。然后找一张image(modify image)用GD方法，让它在hidden layer output是你设下的target)。这样做的话就是让CNN夸大化它所看到的东西。本来它已经看到某一个东西了，你让它看起来更像它原来看到的东西。本来看起来是有一点像东西，它让某一个filter有被active，但是你让它被active得更剧烈(夸大化看到的东西)。

如果你把这张image拿去做Deep Dream的话，你看到的结果是上面这样。右边有一只熊，这个熊原来是一个石头(对机器来说，这个石头有点像熊，它就会强化这件事情，所以它就真的变成了一只熊)。
Deep Dream还有一个进阶的版本，叫做Deep Style。

Deep style

input一张image，再input一张image，让machine去修改这张图，让它有另外一张图的风格 (类似于风格迁移)。

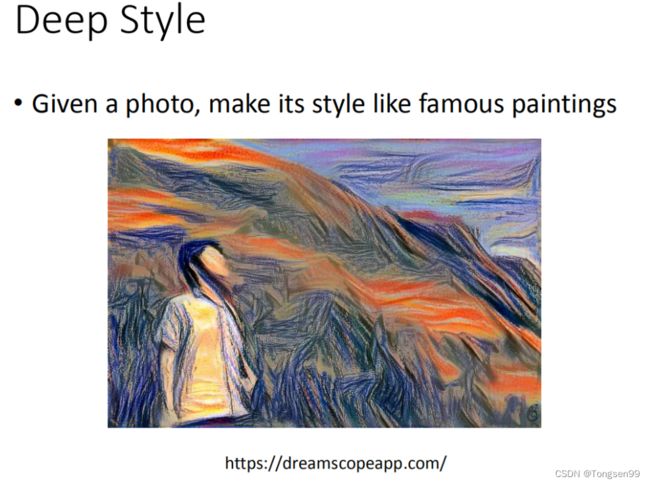
其中做法的精神是这样的：原来的image丢给CNN，然后得到CNN的filter的output，CNN的filter的output代表这张image有什么content。接下来把呐喊这张图也丢到CNN里面，也得到filter的output。我们并不在意一个filter，而是在意filter和filter之间的convolution，这个convolution代表了这张image的style。
接下来用同一个CNN找一张image，这张image它的content像左边这张相片，但同时这张image的style像右边这张相片。找一张image同时可以maximize左边的图，也可以maximize右边的图。得到的结果就是这张图。

CNN的应用

• 围棋

• 语音

• 文本

典型CNN

• LeNet
• AlexNet
• VGGNet
• ResNet